【必学数据结构与算法】栈、队列和数组

栈、队列和数组

• 你将学到什么？（要求）
  1. 理解栈、队列和数组的概念
  2. 理解栈和队列的顺序存储结构和链式存储结构
  3. 掌握栈和队列的基本操作在顺序存储结构和链式存储结构上实现
  4. 掌握矩阵的压缩存储（连载中，因为我还没搞透彻）
• 栈的基本概念

        栈（Stack）是运算受限的线性表，这种线性表的插入和删除操作限定在表的一端（通常为栈顶），另一端则是栈底。不含任何数据元素的栈为空栈。处于栈顶位置的数据元素为栈顶元素。栈的删除操作常称为弹栈（或出栈），栈的插入操作常称为压栈（或入栈）。

【例一】

        饭店里，有一个服务员在洗盘子，洗好的盘子放在桌子上，每洗一个摞一个（类似于插入操作），厨师使用盘子时总是在最上面拿走一个盘子（这个盘子是栈顶元素，这个操作是删除操作）。

思考一下，栈这种结构常用哪些操作呢？

• 栈的基本运算

1. 初始化InitStack（）：构造一个空栈
2. 判断栈空EmptyStack（S）：判断S是否为空栈，如果是返回1，如果不是返回0
3. 压栈Push（S，e）：将元素e插入栈S中，使e为栈顶元素
4. 弹栈Pop（S）：删除栈顶元素
5. 取栈顶GetTop（S）：返回栈顶元素

 

• 栈的顺序实现

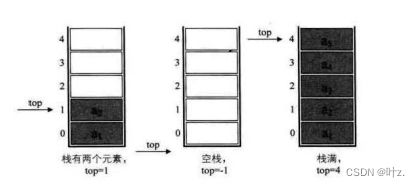
        栈的顺序存储实现是用一段连续的存储单元（常用数组）一次存放栈中的每个元素，并用起始端为栈底。栈的顺序存储结构称为顺序栈。通常用一个一维数组和一个记录栈顶位置的变量实现栈的顺序存储。

        我们定义一个游标变量top用来表示栈顶的位置，如同游标卡尺的游标，它可以来回移动，意味着栈顶的top也可以变大变小，但无论如何游标怎么变化不能超出尺的长度。若栈的长度为MAXSIZE，则栈顶top必须小于MAXSIZE，当栈存在一个元素时top可以是0，也可以是1。因此通常把空栈的判断条件定为top==-1或者top==0。（下面的例子栈初始值将为top==-1）。

 

        注：如果栈为空时，执行弹栈操作将产生下溢错误，如果栈为满则会产生溢出错误。我们要注意这一点，进行判断消除这种可能。

• 顺序栈的运算实现

【例二】计算器结果的顺序栈运算实现

#define MAXSIZE 10
typedef struct
{
	double comeout;
}DM;
typedef struct
{
	DM data[MAXSIZE];
	int top;
}SeqStack;

初始化InitStack（S）：构造一个空栈

void InitStack(SeqStack *S)
{
	S->top = -1;
}

判断栈空EmptyStack（S）：判断S是否为空栈，如果是返回1，如果不是返回0

int EmptyStack(SeqStack *S)
{
	if (S->top == -1)
		return 1;
	else
		return 0;
}

压栈Push（S，e）：将元素e插入栈S中，使e为栈顶元素

//实现思路：如果栈不为满，top自增1，把数据存入进去

void Push(SeqStack *S, DM e)
{
	if (S->top == MAXSIZE)
	{
		cout << "栈满" << endl;
		exit(0);
	}
	else
	{
		S->top++;
		S->data[S->top] = e;
	}
}

弹栈Pop（S）：删除栈顶元素

void Pop(SeqStack *S)
{
	if (S->top == -1)
	{
		cout << "下溢" << endl;
exit(0);
	}
	else
	{
		S->top--;
	}
}

取栈顶GetTop（S）：返回栈顶元素

DM NULLData;
DM GetTop(SeqStack *S)
{
	if (S->top == -1)
	{
		cout << "空栈" << endl;
		exit(0);
		return NULLData;
	}
	else
	{
		return S->data[S->top];
	}
}

【例三】在某些应用中，为了节省空间，让两个数据元素类型一致的栈共享一个数组空间data[max]，成为双栈，两个站的栈底分别是数组的两端，让这两个栈彼此迎面“增长”，两个栈的栈顶变量分别是top1，top2，仅当两个栈的栈顶位置相遇时（top1+1==top2）才发生溢出，如下图。

 

• 栈的链式存储实现

        栈的链式存储实现又称为链栈，链栈可以用带头结点的单链表来实现，top指向链表的头结点，首结点是栈顶结点，top->next指向栈顶结点，尾结点为栈底结点。各个结点由指针域链接，由于每个结点空间是动态分配的，所以不用担心会有溢出。

 

【例四】计算器结果的链栈运算实现

typedef struct
{
	double comeout;
}DM;
typedef struct Node
{
	DM data;
	struct Node *next;
}*LinkStack;
LinkStack head;

• 栈的链式存储结构算法实现

初始化InitStack（L）：构造一个空栈，构造一个带头结点的空链表。

void InitStack(LinkStack L)
{
	L = new Node;
	L->next = NULL;
}

判断栈空EmptyStack（L）：判断S是否为空栈，如果是返回1，如果不是返回0

int EmptyStack(LinkStack L)
{
	if (L->next == NULL)
		return 1;
	else
		return 0;
}

压栈Push（L，e）：将元素e插入栈S中，使e为栈顶元素

//实现思路：为插入数据申请新的结点空间，并进行初始化（本例略），然后使用头插法，新增结点始终插入到头结点后，栈顶结点前。

void Push(LinkStack L, DM e)
{
	Node *newnode;
	newnode = new Node;
	newnode->data = e;
	newnode->next = L->next;
	L->next = newnode;
}

弹栈Pop（L）：删除栈顶元素

//实现思路：删除头结点后的结点，重新链接（跟链表的删除操作一样）。

void Pop(LinkStack L)
{
	if (EmptyStack(L)==1)
	{
		cout << "栈空" << endl;
		exit(0);
	}
	else
	{
Node *temp;
		temp = L->next;
		L->next = temp->next;
		delete temp;
	}

取栈顶GetTop（L）：返回栈顶元素

DM NULLData;
DM GetTop(LinkStack L)
{
	if (EmptyStack(L) != 1)
	{
		return L->next->data;
	}
	else
	return NULLData;
}

• 栈的简单应用

【例五】阅读下列程序片断，写出程序的运行结果

const int maxsize = 50;
typedef struct seqstack
{
	char data[maxsize];
	int top;
}SeqStk;
int main()
{
	SeqStk stk;
	int i;
	char ch;
	InirStack(&stk);
	for (ch = 'A'; ch <= 'A' + 10; ch++)
	{
		Push(&stk, ch);
		printf("%c", ch);
	}
	printf("\n");
	while (!EmptyStack(&stk))
	{
		ch = Gettop(&stk);
		Pop(&stk);
		printf("%c", ch);
	}
	printf("\n");
	return 0;
}

答案：KJIHGFEDCBA

【例六】写一个算法，可以把单链表内所有元素逆置。

【分析】将链表逆置，其实是将链表结点中的数据元素逆置，由于不知道链表长度，可以使用链栈来实现。扫描链表，将链表中的元素依次入栈，然后再遍历链表，将出栈元素存入单链表就可以了。

void ReverseList(LkStk *head)
{
	LkStk *S;
	DataType *S;
	InitStack(S);
	p = head->next;
	while (p->NULL)
	{
		Push(S, p->data);
		p = p->next;
	}
	p = head->next;
	while (!EmptyStack)
	{
		p->data = GetTop(S);
		Pop(S);
		p = p->next;
	}
}

• 队列的基本概念

        队列（Queue）是有限个同类型数据元素的线性序列，是一种先进先出的线性表，新加入的数据元素插入队列的尾端，出队列的数据元素在队列的首部。见下图。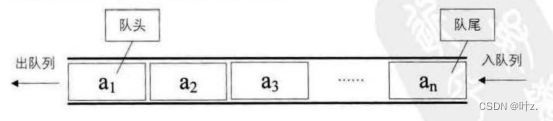

 

        排队的规则是不允许“插队”，先到先得。队列就是这样子的。

• 队列的顺序实现

        顺序存储实现的队列称为顺序队列，它是由一个一维数组（用来存储队列中的元素）及两个分别指示队列首和队列尾数据元素的变量组成，这两个变量分别称为“队列首指针”和“队列尾指针”。我们下面写一个排队叫号系统的队列实现。

【例七】排队叫号系统的顺序实现

#define MAXSIZE 15
typedef struct
{
	int number;
}node;
typedef struct
{
	node data[MAXSIZE];
	int front, rear;
}SeqQueue;

        顺序列表有三个域：data，front，rear。其中data是一个一维数组，存储队列中的数据，front和rear定义为整型变量，实际取值不能超过队列的长度。为了方便操作，规定front指向队列首元素的前一个结点，rear指向队列尾元素结点。初始化rear==0表示空队列，队列满是rear==MAXSIZE-1.

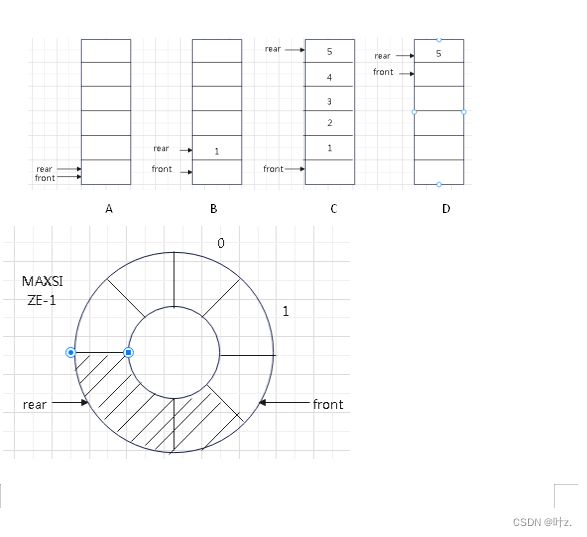
        在队列的顺序存储结构的入队列和出队列操作（见十一、队列的顺序存储算法实现）中会有一个很大的问题，A图是一个空队列，现在向队列插入一条数据得到B，插入5条数据（MAXSIZE==6）这时队列满，不能插入数据。将1—4出队列，得到D，此时要想rear=rear+1，rear将超出数组的下标范围，从而使新元素无法进入队列，此时，数组中还有空位置，这个现象叫做“假溢出”。若要插入新的元素应将现有元素向队列首方向移动。为了避免元素移动所造成的效率低下，可以使存储队列元素的一维数组首位相接，形成一个环状，称为循环队列。Rear==MAXSIZE-1时，只要数组中还有空闲空间，仍可进行入队列操作。此时只需令rear==0，即把data[0]作为新的队尾，将入队元素置于此单元就解决了“假溢出”问题。

根据上述想法，循环队列的入队操作语句应为：

rear=(rear+1)%MAXSIZE;

data[rear]=x;

出队操作应为：

front=(front+1)%maxsize;

循环队列空的条件：

rear=front

循环队列满的条件：

(rear+1)%maxsize=front

循环队列的元素个数：

（rear-front+size）%size

• 循环队列的顺序存储算法实现

        队列初始化InitQueue（Q）：设置一个空队列Q

void InitQueue(SeqQueue &Q)
{
	Q.front = 0;
	Q.rear = 0;
}

        判队列空EmptyQueue（Q）：若队列为空返回1，否则返回0

int EmptyQueue(SeqQueue &Q)
{
	if (Q.rear == Q.front)
		return 1;
	else
		return 0;
}

        入队列EnQueue（Q，x）：将数据元素插入队列

void EnQueue(SeqQueue &Q, node x)
{
	if (EmptyQueue(Q))
	{
		Q.rear = (Q.rear + 1) % MAXSIZE;
		Q.data[Q.rear] = x;
	}
	else
	{
		cout << "队列满" << endl;
		exit(0);
	}
}

        出队列OutQueue（Q）：删除队列首元素

void OutQueue(SeqQueue &Q)
{
	if (EmptyQueue(Q))
	{
		cout << "队列空" << endl;
		exit(0);
	}
	else
		Q.front = (Q.front + 1) % MAXSIZE;
}

        取队列首元素GetHeadForQueue（Q）：返回队列首元素

node GetHeadForQueue(SeqQueue &Q)
{
	if (EmptyQueue(Q))
	{
		cout << "队列空" << endl;
		return NULLnode;
	}
	else
		return Q.data[(Q.front + 1) % MAXSIZE];
}