2020年数维杯国际大学生数学建模C题城市道路最佳除雪方案求解全过程文档及程序
2020年数维杯国际大学生数学建模
C题 城市道路最佳除雪方案
原题再现:
近日,中国北方出现大规模强降雪。在一些地区,降雪量超过了20厘米。世界极端天气的频繁发生,预示着未来发生大雪的可能性在急剧增加。这场大规模的大雪给我国城市化水平较高的地区带来了诸多不便。由于除雪工作的延误,造成道路堵塞,严重影响了居民的日常生活。在许多地方,例如长春市,已经暂停工作和学校由于大雪。图1显示了某城市大雪后的道路状况。
为确保市民通行顺畅,环卫人员变身“清雪部队”,争分夺秒地与冰雪“战斗”,努力清理和运走积雪,努力做到停雪清路。为了达到停雪后道路畅通的目的,需要制定科学合理的道路除雪计划。除雪的方法因雪的深度而异。当积雪深度较小时,可以简单地把路中间的积雪扫到路边的绿化带或休闲区。然而,当积雪深度增加,很难临时存储的绿带,需要使用一个雪犁收集雪倒进一辆大卡车运输到一个大型开放空间内部或外部的城市。
附件1提供了某城市的道路信息,包括交叉口的经纬度,交叉口的连接,交叉口的宽度,潜在积雪的位置。请尝试通过数学建模解决以下四个问题:
(1)请结合附件1的数据,提供一个合理的清扫方案,假设雪可以清扫到附近的绿化带或休闲区,并且清扫车辆的数量是固定的。
(2)请提供最优的扫雪机、运输车辆和环卫工人分配方案,以便在雪量较大且市政卫生对扫雪机、运输车辆和环卫工人配置较为固定的情况下,尽快完成扫雪机任务。
(3)在实际的道路清洁过程中,我们经常会遇到道路两侧停放车辆的情况(图2),这无疑会增加道路清洁的难度,而且城市的停车位数量非常有限。能否提供一个合理的除雪计划,以便提前清理停在道路两旁的车辆,同时尽快恢复停车位的使用?
(4)城市立交桥较多,坡道明显,不同道路清洁优先级不同。附件2给出了不同路段的优先等级(1级表示最不重要,6级表示最重要)。你能提供一个最佳的除雪计划,考虑到路段的优先等级吗?
提交的文件应包括:
页表
目录
1—2页的文章
您的解决方案不超过20页,最多24页的摘要,目录,文章
注意:参考列表和任何附录不计入页面限制,应该出现在您的完整解决方案之后。您不应该使用未经授权的图像和材料,其使用受到版权法的限制。确保你在报告中引用了你的想法和材料的来源。
整体求解过程概述(摘要)
基于城市地区扫雪系统的任务和道路分布,构建了清洗车道选路模型分析,探讨了总距离最短、最短时间内清扫车操作系统的运行方案。然后,结合相关约束条件,给出最优路径方案。
为了解决第一个问题,基于节点位置和连接表,在建立模型之前,需要将问题中每个点之间的连接关系及其关系转换为数学中的加权直接图。由于网络相对密集,使用弗洛伊德算法计算每侧的权重,即两个连接点之间的距离权重。考虑到每条道路的宽度不同,根据道路的宽度在每条道路的距离数据中加入一定的宽度权重,得到最终的距离权重。结合目标函数和约束条件,使用Dijkstra和遗传算法求解Matlab中最短的总里程。在这种情况下,最短的总里程为2178.1347km。
对于问题二,在积雪量大的情况下,会有积雪点,然后根据问题一中车辆的最佳路径,需要扫雪车、卡车和环卫工人进行联合作业。根据运输车辆的最优路径约束条件,建立新的目标函数。使用Dijkstra和遗传算法求解Matlab中最短的总里程,本例中最短的总里程为2746.0036km。
对于问题三和问题四,都是基于问题一,结合需求弧的优先级(道路的优先级),基于新的目标函数和约束条件建立新的数学模型。根据变量和约束的复杂性,建立了一种新的基于并行和遗传算法的启发式算法,然后,利用整个过程找到解决清洁所需最短时间的最佳方法。获得第三个问题的最短时间为6.99h,而第四个问题的最短时间为5.92h。
模型假设:
1.假设问题中给出的网络是一个操作区域和一个站点,其位置已经规划好。
2.假设所有清扫车、犁、运输车和环卫工人都以相同的速度运行。
3.假设在清洁过程中,每条路径对应一辆汽车,即每辆车只服务于相同的路径。车辆从车站出发,完成路径清理作业,最后返回车站。
4.假设多次访问该部分,但该部分仅提供一次。
5.假设道路的所有路段都是双向车道,并且它们之间有一个分隔区。
问题分析:
城市道路除雪是一个非常复杂的系统,其机制和模式的优化影响着城市的运行和发展。在这一部分中,我们将分析这些问题,为以后的研究提供思路。
数据分析
首先,我们对数据进行了预处理。根据问题中给出的城市道路信息,包括交叉路口的经纬度、交叉路口的连接关系、交叉路口的宽度和潜在积雪的位置。使用Matlab软件处理交叉点的经纬度,将其转换为笛卡尔坐标点,如图2-1所示。

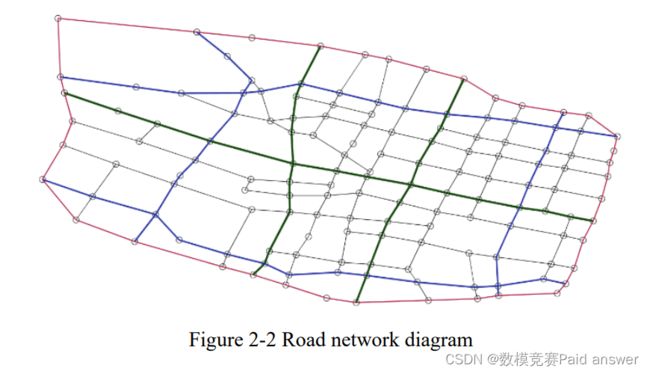
然后,我们处理了交点的连接关系,得到交点的宽度(即两个交点的宽度),如图2-2所示。
模型的建立与求解整体论文缩略图
全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:
部分Matlab程序如下:
clc,clear
link=xlsread("links.xls");
sj0=xlsread("Attachment 1.xlsx");
loc_nodes=xlsread("Attachment 1.xlsx");
startnode=link(:,1);
endnode=link(:,2);
width=link(:,3);
HU=zeros(241,3);
HU(:,1)=startnode;
HU(:,2)=endnode;
HU(:,3)=width/2;
ZOHU=sum(HU);
ZOHU1=ZOHU(1,3);
link1=zeros(141);
for n=1:241
link1(startnode(n),endnode(n))=1;
end
link1=link1+link1';
x=sj0(:,2); x=x(:);
y=sj0(:,3); y=y(:);
kb=5;
sj=[x y];
sj=sj*pi/180;
d=zeros(141);
d1=zeros(141);
for i=1:140
for j=i+1:141
d(i,j)=6370*acos(cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2)));
end
end
d=d+d';
for i=1:140
for j=i+1:141
if link1(i,j)==1
d1(i,j)=d(i,j);
end
if link1(i,j)==0
d1(i,j)=inf;
end
end
end
d1=d1+d1';
M_PI=3.14159265358979323846;
xlab=loc_nodes(:,2);
ylab=loc_nodes(:,3);
position=[xlab ylab];
L = 6381372 * M_PI * 2;
W = L;
H = L / 2;
mill = 2.3;
n=size(position,1);
new_position=[];
figure
for i =1:n
lon=position(i,1);
lat=position(i,2);
x = lon * M_PI / 180;
y = lat * M_PI / 180;
y1 = 1.25 * log(tan(0.25 * M_PI + 0.4 * y));
dikaerX(i) = (W / 2) + (W / (2 * M_PI)) * x ;
dikaerY(i) = (H / 2) - (H / (2 * mill)) * y1 ;
new_position(i,1)=dikaerX(i);
new_position(i,2)=dikaerY(i);
plot(dikaerX(i),dikaerY(i),'o','color','k','Markersize',8)
hold on
end
path_0=[0];
path_z=[0];
qi=1;
path_0=[qi];
dist_0=zeros(L_1,1);
dist_z=[];
dist1=[];
dist2=[];
xx=[];
yy=[];
c_z=randperm(241);
k=5;
c=c_z(1:k);
c1=c_z(k:241);
for i=1:k
[dist1,~]=mydijkstra(d1,1,HU(c(i),1));
[dist2,~]=mydijkstra(d1,1,HU(c(i),2));
if dist1<=dist2
dd(i,1)=dist1;
elseif dist1>dist2
dd(i,1)=dist2;
end
end
for i=1:k-1
for j=1:k-1-i
if dd(j)>dd(j+1)
tt=c(j);
c(j)=c(j+1);
c(j+1)=tt;
end
end
end
for i=1:k
[dist1,mypath1]=mydijkstra(d1,qi,HU(c(i),1));
[dist2,mypath2]=mydijkstra(d1,qi,HU(c(i),2));
a_1=size(mypath1);
a_2=size(mypath2);
if dist1==0
path_0=[path_0,HU(c(i),2)];
qi=HU(c(i),2);
end
if dist2==0
path_0=[path_0,HU(c(i),1)];
qi=HU(c(i),1);
end
if dist1=dist2&&dist2~=0
dist_0(1,1)=dist_0(1,1)+dist2;
path_0=[path_0,mypath2(2:a_2(1,2)-1),HU(c(i),2),HU(c(i),1)];
qi=HU(c(i),1);
end
end
[dist1,mypath1]=mydijkstra(d1,qi,1);
a_1=size(mypath1);
dist_0(1,1)=dist_0(1,1)+dist1;
path_0=[path_0,mypath1(2:a_1(1,2))];
xx=new_position(path_0,1);yy=new_position(path_0,2);
plot(xx,yy,' -','color','b','linewidth',3);
clear path_0;
path_0=[qi];
for i=1:145
[dist1,mypath1]=mydijkstra(d1,qi,HU(c1(i),1));
[dist2,mypath2]=mydijkstra(d1,qi,HU(c1(i),2));
a_1=size(mypath1);
a_2=size(mypath2);
if dist1==0
path_0=[path_0,HU(c1(i),2)];
qi=HU(c1(i),2);
end
if dist2==0
path_0=[path_0,HU(c1(i),1)];
qi=HU(c1(i),1);
end
if dist1=dist2&&dist2~=0
dist_0(1,1)=dist_0(1,1)+dist2;
path_0=[path_0,mypath2(2:a_2(1,2)-1),HU(c1(i),2),HU(c1(i),1)];
xx=[xx;new_position(mypath2,1);new_position(HU(i,1),1)];
yy=[yy;new_position(mypath2,2);new_position(HU(i,1),2)];
qi=HU(c1(i),1);
end
end
xx=new_position(path_0,1);yy=new_position(path_0,2);
plot(xx,yy,' -','color','y');
c=randperm(95);
qi=1;
clear path_0;path_0=[qi];
for i=1:95
[dist1,mypath1]=mydijkstra(d1,qi,HU(c(i),1));
[dist2,mypath2]=mydijkstra(d1,qi,HU(c(i),2));
a_1=size(mypath1);
a_2=size(mypath2);
if dist1==0
path_0=[path_0,HU(c(i),2)];
qi=HU(c(i),2);
end
if dist2==0
path_0=[path_0,HU(c(i),1)];
qi=HU(c(i),1);
end
if dist1<dist2&&dist1~=0
dist_0(k,1)=dist_0(k,1)+dist1;
path_0=[path_0,mypath1(2:a_1(1,2)-1),HU(c(i),1:2)];
qi=HU(c(i),2);
end
if dist1>=dist2&&dist2~=0
dist_0(k,1)=dist_0(k,1)+dist2;
path_0=[path_0,mypath2(2:a_2(1,2)-1),HU(c(i),2),HU(c(i),1)];
qi=HU(c(i),1);
end


