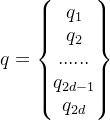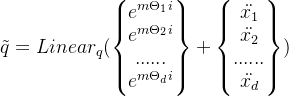超超超超超简单！从结果推导RoPE旋转位置编码
位置编码介绍与绝对位置编码
我们知道，主流大语言模型使用的自注意力机制(self-attention)技术中，缺少位置的信息。而位置信息对于理解语言而言是相当重要的，比如你爱我和我爱你有同样的字却有截然不同的含义，其中的关键就在于字的位置不同，所以缺少位置信息的self-attention是不完整的。并且从我们人类的角度来说，我们阅读时在一段文字上的注意力，肯定是和位置有关的。所以一种传统并且相当直观的方法是在计算self-attention之前给输入加上绝对位置编码，让输入能够带有位置信息，以便于模型理解。
class Decoder(nn.Module):
def __init__(self):
# __init__作用，定义一个词嵌入层，一个位置嵌入层，以及六个decoder layer
super(Decoder,self).__init__()
self.word_emb = nn.Embedding(model_parameters.vocab_size,model_parameters.hidden_size)
self.pos_emb = nn.Embedding(model_parameters.max_pos,model_parameters.hidden_size) # 可以短于，不可以超过
self.decode_layers = nn.ModuleList([DecodeLayer() for _ in range(model_parameters.n_layers)])
def get_emb(self,input_vecs):
input_len = input_vecs.size(1)
pos = torch.arange(input_len,dtype=torch.long, device=device) # 生成一个顺序序列
# 先加维度然后才能expand
pos = pos.unsqueeze(0).expand_as(input_vecs)
pos_emb = self.pos_emb(pos)
word_emb = self.word_emb(input_vecs)
final_vecs = word_emb + pos_emb # 得到batch输入的embedding结果，维度为[batch_size,input_nums,hidden_size]
return final_vecs绝对位置编码的介绍如下：
1.假设我们有一个内容为我爱你
2.将这两个列表经过词嵌入层和位置嵌入层编码，得到两个维度为[seq_len, dim]的张量。
3.将得到的新张量简单相加，我们就得到了最终的带有位置信息的词向量。
4.这个词向量经过自注意力计算后，得到的注意力加权向量仍然会保持原来的位置信息。
使用绝对位置编码的局限性主要在于其不能很好地处理长序列的输入，因为绝对位置编码的大小是固定的，而且在输入序列较长的情况下，绝对位置编码的值可能会越来越大，超出模型能够处理的范围，从而导致数值不稳定和梯度消失等问题。
此外，绝对位置编码也无法很好地处理变长的输入序列，因为这种编码方式是基于序列的位置信息来编码的，而输入序列的长度不同，其位置信息也不同，这可能导致编码方式不一致。因此，如果输入序列的长度不同，那么使用绝对位置编码可能会导致模型性能下降。
苏剑林大神在Roformer论文中提出了一种使用绝对位置编码方式进行相对位置编码的旋转位置编码，至于为什么叫旋转位置编码，且看下文。
RoPE的编码方式
这种编码的初衷如下，假设我们已经计算得到了自注意力机制中的query向量：q以及key向量：k。我们希望能找到任意一种函数
，其中x为任意q或k向量，m为向量在序列中的位置。使得
。换句话说我们希望找到一种q、k向量的编码方式，使任意编码后的qk向量的内积包含他们的相对位置信息
。
经过推导后我们发现了一种编码方式
，有
，![q{\tilde{}}\cdot k\tilde{}=Real[qke^{(m-n)\Theta {i}}]](http://img.e-com-net.com/image/info8/629c7a305ca54b10986f797b5b5d0bc0.png){kind=small}
，![Real[*]](http://img.e-com-net.com/image/info8/0191362d2492485eaa48b53c9905d2b6.png){kind=small}
表示*的实部。可以看到，经过这样编码之后新向量的内积自动包含了相对位置的信息。查看RoPE的最终编码方式，我们可以很直观的发现使用复数来进行位置编码的原因，因为这样可以很好的利用到复数的幅角相加性质来引出相对位置的信息，我们也可以从这点来窥探RoPE作者的动机，也有助于我们更好理解这种编码。(由于
求点积等于
与
的共轭复数相乘的实部，所以最终结果是幅角相减，详见附录1.5）。
当我们把运算推广到高维场景，假设我们有：
我们令q中元素两两组合为复数
再与对应的旋转向量相乘，我们有：
这就是我们的最终编码实现方式，其中
沿用《Attention is all you need》论文提出的Sinusoidal编码的设置：
，d为向量的长度
RoPE编码和Sinusoidal编码非常像，Sinusoidal编码为：
如果你对数学推导不感兴趣，你可以直接跳过RoPE的推导过程，阅读本文以上内容已经足以进行工程实践，并且理解这种编码确实实现了使用绝对位置编码方式实现相对位置编码。
RoPE编码推导过程
我们的目标是找到任意一种二元函数
满足
为了找到一种最简单并且最直观的实现。我们需要给这个函数加一些约束条件。所以我们规定：
。
首先假设所有的q,k向量都是二维向量以方便我们进行推导，在不知道具体表达式时我们可以使用
以及
来事先表示编码后的复向量，通过求它们的内积，我们有：
![R_{g(q,k,m-n)}e^{\theta_{g(q,k,m-n)}i}=R_{f(q,m)}R_{f(k,n)}[e^{(\theta_{f(q,m)}-\theta_{f(k,n)})i}-sin{(\theta_{f(q,m)}-\theta_{f(k,n)})}i]](http://img.e-com-net.com/image/info8/b6a50916785249499dccb8d6d2850139.png){kind=small}
0)式
在Roformer论文中，为了简单起见，对目标函数了进行如下调整：
1）式
在1)式中令左端模长等于右端模长，当m=n时我们有：
2)式
也就是说我们只要找到一种编码前和编码后向量模一致的编码就可以满足我们的目的，这是多么简单啊！
同样，在1)式中令左端幅角等于右端幅角，当m=n时我们有：
3)式
此时我们可以发现：
4)式
也就是说编码前的向量的幅角与编码后的向量的幅角的差值是于向量本身无关的，只与位置相关。
所以我们可以设一个函数
来表示这种差值。当我们令n=m-1时，我们改写4)式可以得到以下公式：
5)式
易知5)式右端为一定值，且
也就是说
是一个初值为0的等差数列！
求出之后我们知道
，所以
【注：
】
且由于
是一个等差数列，所以我们可以设差为一定值
，那么我们可以得到
，由于复向量的相乘从几何上代表着旋转与伸缩，RoPE编码中的复向量乘法意为着向量的旋转，所以我们可以将与
相乘的
为旋转向量
容易引起混淆并且也困扰了笔者很久的一点是，此时找到的
等于的是
与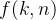
的共轭复数相乘，已经偏离了我们最开始的目标。但是我们找到的与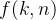的内积仍然包含了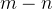的相对位置信息。
代码实现
import torch
from typing import Union, Tuple
"""
作者: hhn
本代码实现借鉴于llama,地址:https://github.com/facebookresearch/llama/blob/main/llama/model.py#L131, 我在llama的实现上稍作修改使其有更好的易读性。
RoPE论文地址:https://arxiv.org/abs/2104.09864, 博客地址:https://spaces.ac.cn/archives/8265/comment-page-3#comments
RoPE:对于q,k向量,我们需要一个f(x,pos)=x_pos_emb[其中x为任意q,k向量],使得 == g(q,k,m-n)。
其中表示两个向量求内积,m与n分别为q和k在输入序列中的位置,m-n为他们的相对位置。
推导可以知道有一个f(q,m) = qe**(m(theta_i)i)满足f(q,m)f(k,n) == g(q,k,m-n),其中theta_i为和i有关的常量
theta_i == 10000.0**(-2i/d), 其中i为q向量中元素的位置,d为q向量的长度,也就是attention的维度
当把q看作复平面上的复向量,则f的作用相当于令q和1e**(m(theta_i)i) == cos(m(theta_i)) + sin(m(theta_i))i相乘
从复向量的角度来说相当于是把q旋转了一定的角度,所以我将1e**(m(theta_i)i)称为旋转向量
"""
THETA = 10000.0
def get_origin_rotate_vecs(
atten_dim: int,
seq_len: int,
theta: Union[None,int]=None
) -> torch.Tensor:
"""
作用：求旋转向量
输入: atten_dim->注意力q/k向量的维度, seq_len->输入序列的长度
输出：旋转向量
"""
# 论文中的rope实现方式
if theta is None:
theta = THETA
theta_i_e = (torch.arange(0,atten_dim,2)[:(atten_dim // 2)].float() / atten_dim) * -1
freqs = theta_i = theta ** theta_i_e
position = torch.arange(seq_len) # [0, 1, 2, 3, ..., seq_len]
freqs = torch.outer(position,freqs).float() # 求向量的外积,维度为[seq_len,atten_dim]
freqs_cis = torch.polar(torch.ones_like(freqs),freqs) #将上一步的结果写成复数的形式,模是1幅角是freqs
return freqs_cis.view(1,1,seq_len,atten_dim//2)
def apply_rope(
q: torch.Tensor,
k: torch.Tensor,
rotate_vecs: torch.Tensor
) -> Tuple[torch.Tensor,torch.Tensor,torch.Tensor]:
"""
作用: 将q,k向量分别与旋转向量相乘,得到旋转后的q,k向量q/k_rotated。然后进行点乘得到具有位置信息的attention分数
输入: q->weight_q(input_vecs), k->weight_k(input_vecs), rotaed_vecs->旋转向量
输出: 注意力分数
"""
# 计算过程q:[batch_size,atten_heads,seq_len,atten_dim]->q_complex:[b,a_h,s,a_d//2,2]->[b,a_h,s,a_d//2]->[b,a_h,s,a_d//2,2]
q_complex = torch.view_as_complex(q.float().reshape(*q.shape[:-1], -1, 2)) #[batch_size,atten_heads,seq_len,atten_dim//2,2]
k_complex = torch.view_as_complex(k.float().reshape(*k.shape[:-1], -1, 2)) # 将一个大小为n的向量两两组合形成复数来计算
# 位置编码只和向量的序列位置还有向量本身有关，和batch以及注意力头无关，所以只用关注第二维和第四维
q_rotated = torch.view_as_real(q_complex*rotate_vecs).flatten(3) # 恢复成原来的样子，将第三维之后压平，也就是(atten_dim//2,2)->(atten_dim)
k_rotated = torch.view_as_real(k_complex*rotate_vecs).flatten(3)
attention_score = torch.matmul(q_rotated, k_rotated.transpose(-1,-2))
return q_rotated.type_as(q), k_rotated.type_as(q), attention_score.type_as(q)
if __name__ == '__main__':
# 代码的示例使用，直接运行可以看到示例输出
atten_dim = 64
atten_heads = 1
batch_size = 1
seq_len = 50
q = torch.rand(batch_size,atten_heads,seq_len,atten_dim)
k = torch.rand(batch_size,atten_heads,seq_len,atten_dim)
rotate_vecs = get_origin_rotate_vecs(seq_len=seq_len,atten_dim=atten_dim)
q_rotated, k_rotated, atten_score = apply_rope(q,k,rotate_vecs)
print(atten_score) 附录
理解RoPE需要的复数知识：
1.任意一个二维向量x，我们可以通过极坐标找到它的复数表示方法
，
为其模的大小，
为其幅角的度数。
2.并且这种复数表示方法有一种等效的表示
。
3.可以用泰勒公式稍微验证一下这两种表达式的等效性：
1).
2).
3).
4).
4.假设有两个复数 
，乘积为
,其中，
和 
分别表示两个复数的模长，
和
分别表示它们的幅角。
5.两个复数q，k的内积等于q乘k的共轭复数的实部。所以
声明
笔者数学能力有限，文章中若有错漏之处，欢迎提出探讨！