平衡二叉树和AVL
目录
-
- 一、AVL
- 二、平衡二叉树
- 三、代码实现
- 四、测试
- 五、AVL的左旋转和右旋转
-
- (1)维护平衡的时机
- (2)插入的元素在不平衡节点的左侧的左侧
- 右旋代码实现
- (3)插入的元素在不平衡节点的右侧的右侧
- 左旋代码实现
- 六、LR和RL
-
-
- 1、**插入的元素不在平衡节点的左侧的右侧**
- 2、**插入的元素在不平衡结点的左侧的右侧**
- 代码实现
-
- 七、AVL树的删除
- 八、测试
- 九、完整代码
平衡二叉树和AVL树是在二分搜索树的基础上进行讲解
回忆二分搜索树的问题:
添加数据 :是按照顺序添加的 32145
每个节点的左节点小于根节点,每个节点的右节点都大于根节点
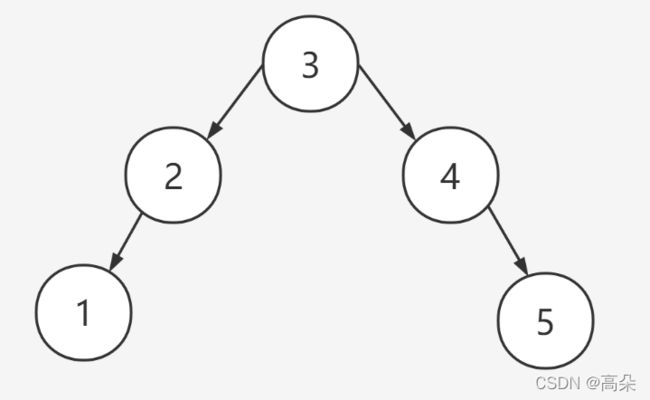
一、AVL
AVL树得名于它的发明者G.M.Adelson-Velsky 和 E.M.Landis
AVL树最早发明的自平衡二分搜索树
二、平衡二叉树
平衡二叉树的要求:对于任意一个节点,左子树和右子树的高度差不能超过1
(1)一颗满二叉树和完全二叉树是平衡二叉树

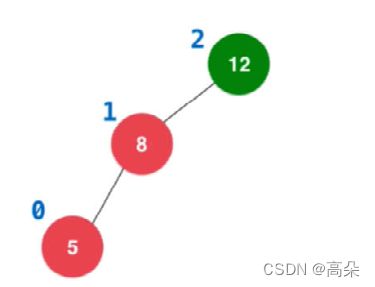
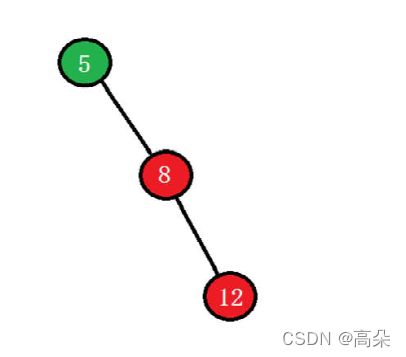
(3)如果按照以前的二分搜索树的方式,分别添加节点 2 和 7 ,此棵树就不是平衡二叉树。
为了能保持这课二叉树的平衡,就要标注每个节点的高度

计算出平衡因子(左右子树的高度差) 最终高度差不能相差1

三、代码实现
(1)获取节点高度
//获取节点高度
private int getheight(Node node) {
if (node == null) {
return 0;
}
return node.heigth;
}
(2)获取节点的平衡因子
//获取平衡因子
private int getBalance(Node node) {
if (node == null) {
return 0;
}
return getheight(node.left) - getheight(node.right);
}
(3)判断是不是二分搜索树
//判断是否是二分搜索树
public boolean isBST() {
return isBST(root);
}
(4)根据中序遍历的结果进行判断是不是二分搜索树
//中序遍历的结果进行判断 左 中 右
private boolean isBST(Node node) {
List<T> list = new ArrayList<>();
inorderTraversal(node, list);
for (int i = 0; i < list.size() - 1; i++) {
if (list.get(i).compareTo(list.get(i + 1)) > 0) {
return false;
}
}
return true;
}
(5)中序遍历
//中序遍历
private void inorderTraversal(Node node, List<T> list) {
if (node == null) {
return;
}
inorderTraversal(node.left, list);
list.add(node.val);
inorderTraversal(node.right, list);
}
(6)判断是否是平衡二叉树
//判断是否是平衡二叉树
public boolean isBalanceTree() {
return isBalanceTree(root);
}
private boolean isBalanceTree(Node node) {
//如果根节点为空,也为平衡树
if (node == null) {
return true;
}
//根节点不为空情况如下 平衡因子的绝对值
int balance = Math.abs(getBalance(node));
if (balance > 1) {
return false;
}
return isBalanceTree(node.left) && isBalanceTree(node.right);
}
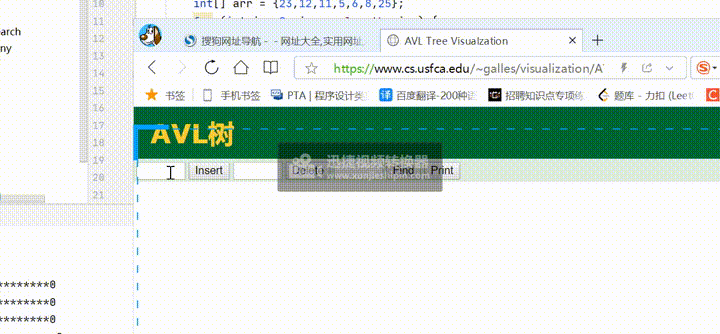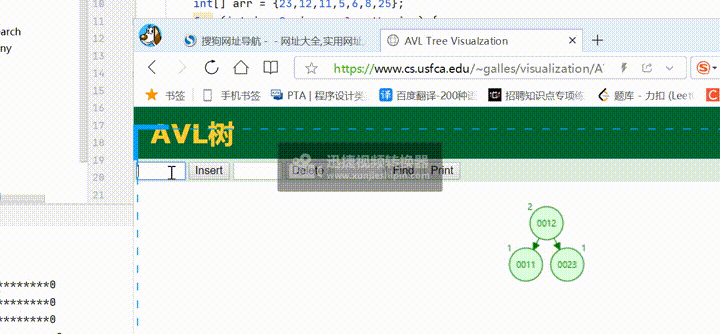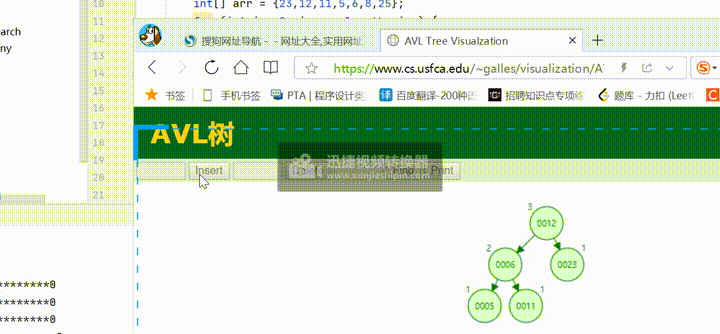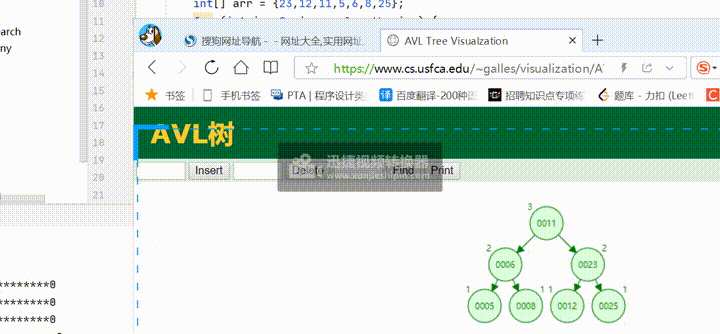
四、测试
AVLtree<Integer> AVLtree =new AVLtree();
int[] arr = {23,12,11,5,6,8,25};
for (int i = 0; i <arr.length; i++) {
AVLtree.add(arr[i]);
}
System.out.println(AVLtree.isBST());
System.out.println(AVLtree.isBalanceTree());
System.out.println(AVLtree);
五、AVL的左旋转和右旋转
(1)维护平衡的时机
加入节点后,沿着节点向上维护平衡性
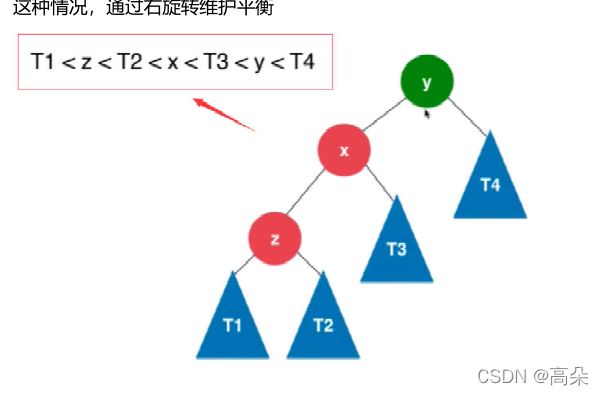
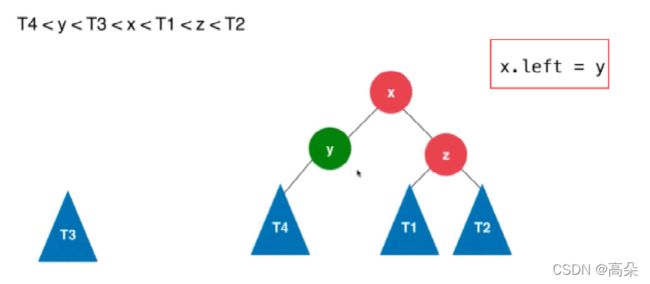
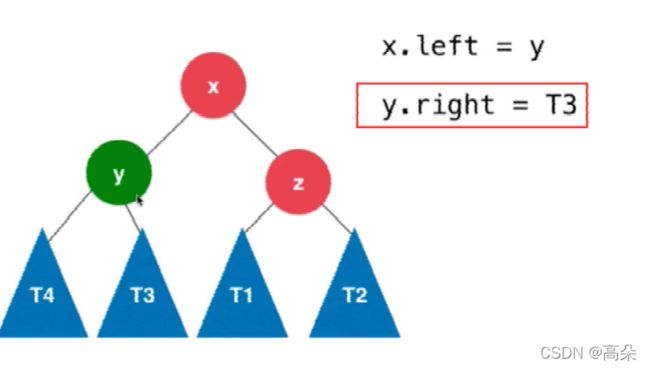
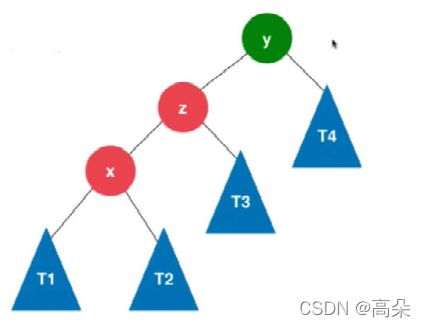
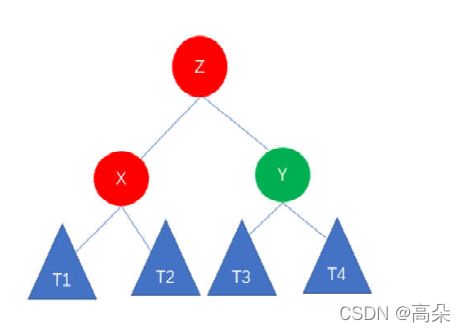
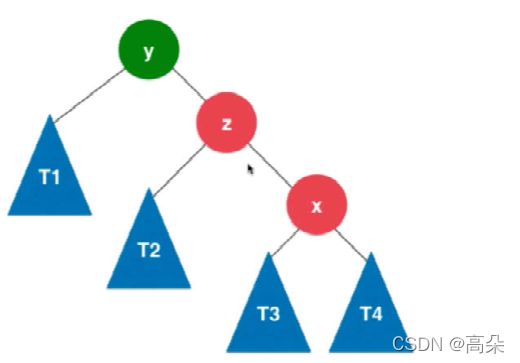
(2)插入的元素在不平衡节点的左侧的左侧
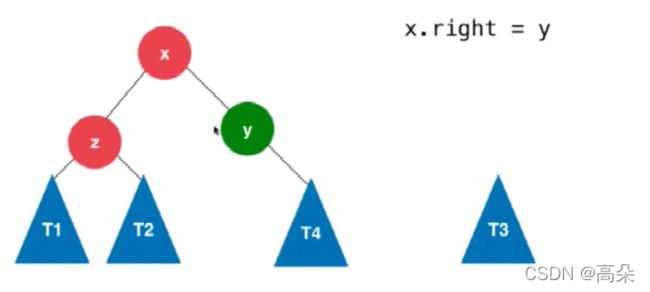
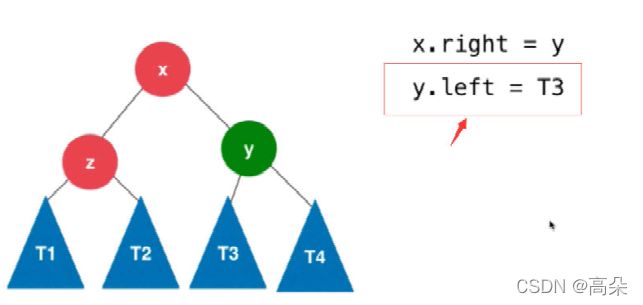
右旋代码实现
//AVL树的右旋 根节点为x
public Node rightrotate(Node x) {
Node y = x.left; //将根节点的左节点赋值为 y节点
Node t2 = y.right; //将y节点的右侧赋值为t2 断开右侧节点
y.right = x; //右旋转,将根节点赋值给y的右侧
x.left = t2; //将断开的t2 ,连接到x根节点的左侧
//更新height
x.heigth = Math.max(getheight(x.left), getheight(x.right)) + 1;
y.heigth = Math.max(getheight(y.left), getheight(y.right)) + 1;
return y;
}
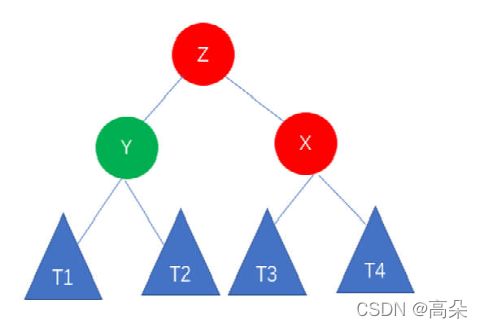
(3)插入的元素在不平衡节点的右侧的右侧
左旋代码实现
//AVL树的左旋
public Node leftrotate(Node x) {
Node y = x.right; //根节点为x ,将根节点的右侧赋值为y节点
Node t2 = y.left; //将y节点的左侧断开 ,并赋值为t2
y.left = x; //将节点x赋值在y节点的左侧
x.right = t2; //将断开的t2 ,连接到x节点的右侧
//更新height
x.heigth = Math.max(getheight(x.left), getheight(x.right)) + 1;
y.heigth = Math.max(getheight(y.left), getheight(y.right)) + 1;
return y;
}
六、LR和RL
1、插入的元素不在平衡节点的左侧的右侧
2、插入的元素在不平衡结点的左侧的右侧
代码实现
因为添加元素会使树变得不平衡,所以在添加中做平衡操作
//1、添加节点
public void add(T ele) {
if (contains(ele) != null) {
return;
}
//利用递归添加节点
root = add(root, ele);
this.size += 1;
}
private Node add(Node node, T ele) {
//如果根节点为空,创建一个新得二叉树,传ele参数进去
if (node == null) {
return new Node(ele);
}
//根节点不为空,将要添加的元素与跟的值进行比较大小
//递归操作 不考虑等于的情况
if (ele.compareTo(node.val) > 0) {
node.right = add(node.right, ele);
} else {
node.left = add(node.left, ele);
}
//更新以node为根的这棵树的高度
node.heigth = Math.max(getheight(node.left), getheight(node.right)) + 1;
//判断是否平衡,不平衡需要作出维护平衡 判断左右旋 还是 右左旋
Node retNode = null;
//右旋
if (getBalance(node) > 1 && getBalance(node.left) >= 0) {
retNode = rightrotate(node);
//左旋
} else if (getBalance(node) < -1 && getBalance(node.right) <= 0) {
retNode = leftrotate(node);
//左右旋
} else if (getBalance(node) > 1 && getBalance(node.left) < 0) {
node.left = leftrotate(node.left);
retNode = rightrotate(node);
//右左旋
} else if (getBalance(node) < -1 && getBalance(node.right) > 0) {
node.right = rightrotate(node.right);
retNode = leftrotate(node);
} else {
retNode = node;
}
return retNode;
}
七、AVL树的删除
/**
* 从以root为根的二分搜索树中删除值为val的节点
*
* @param node
* @param val
* @return
*/
private Node removeNode(Node node, T val) {
Node retNode = null;
//递归到底的情况,找到了删除的节点
//左节点为空,右节点为空,左右节点都为空
if (node.val.compareTo(val) == 0) {
if (node.left == null) {
Node rightNode = node.right;
node.right = null; //删除的为叶子节点
retNode = rightNode;
} else if (node.right == null) {
Node leftNode = node.left;
node.left = null;
retNode= leftNode;
}
else{
//左右节点都不为空
//1、找node 的后继(node.right中的最小节点)
Node t = findminnodeDG(node.right);
//2、node.right 中删除最小节点
// Node node1 = removeMixNode(node.right);
Node rightNodeRoot = removeNode(node.right, t.val); //用递归的方法 删除元素 t.val
//3、使用后继节点替换node
t.left = node.left;
t.right = rightNodeRoot;
//4、生成新树,新树的根节点就是后继节点,返回新树根节点
node.left = node.right = null; //将待删除节点的左右孩子删除 ,断掉关联关系
retNode= t; //返回最终的新节点
}
}else if (node.val.compareTo(val) > 0) {
node.left = removeNode(node.left, val);
retNode =node;
} else {
node.right = removeNode(node.right, val);
retNode = node;
}
//如果待删除的节点为空,返回空,不需要更新树高 ,可能是叶子节点
if (retNode==null){
return null;
}
//更新以node为根的这棵树的高度
retNode.heigth = Math.max(getheight(node.left), getheight(node.right)) + 1;
Node result = retNode;
//右旋
if (getBalance(retNode) > 1 && getBalance(retNode.left) >= 0) {
result = rightrotate(retNode);
//左旋
} else if (getBalance(retNode) < -1 && getBalance(retNode.right) <= 0) {
result = leftrotate(retNode);
//左右旋
} else if (getBalance(retNode) > 1 && getBalance(retNode.left) < 0) {
retNode.left = leftrotate(retNode.left);
result = rightrotate(retNode);
//右左旋
} else if (getBalance(retNode) < -1 && getBalance(retNode.right) > 0) {
retNode.right = rightrotate(retNode.right);
result = leftrotate(retNode);
}
return result;
}
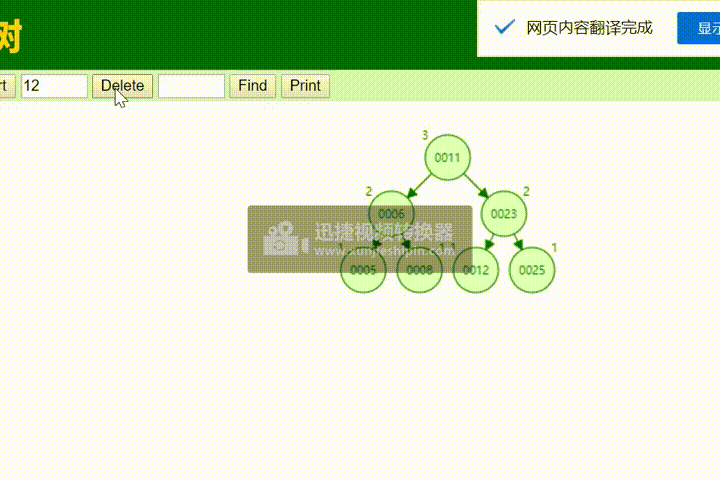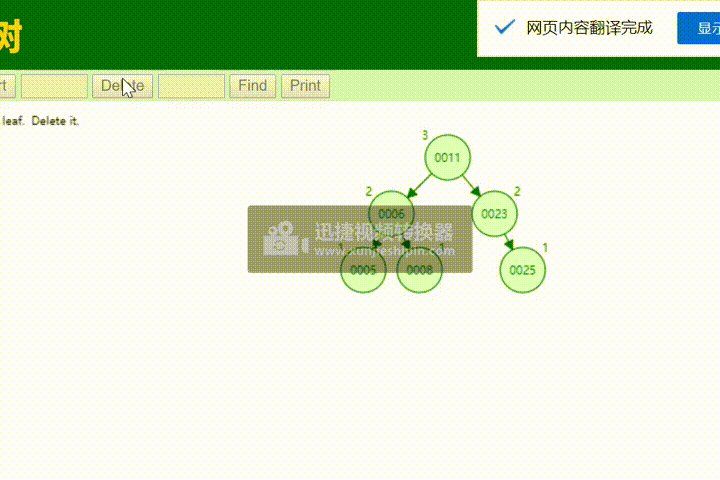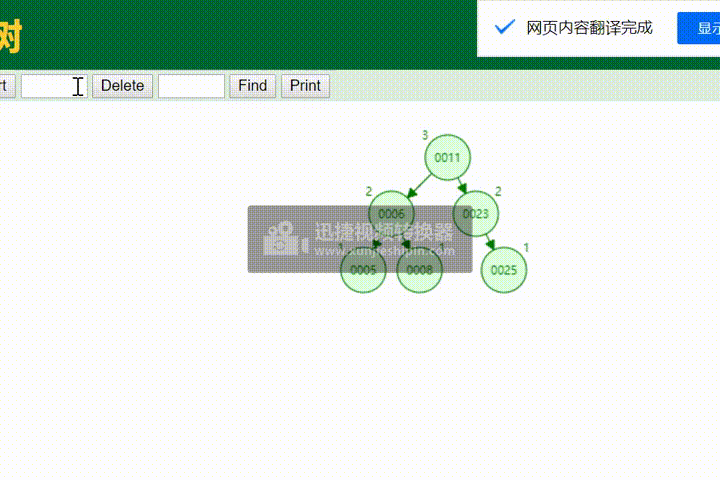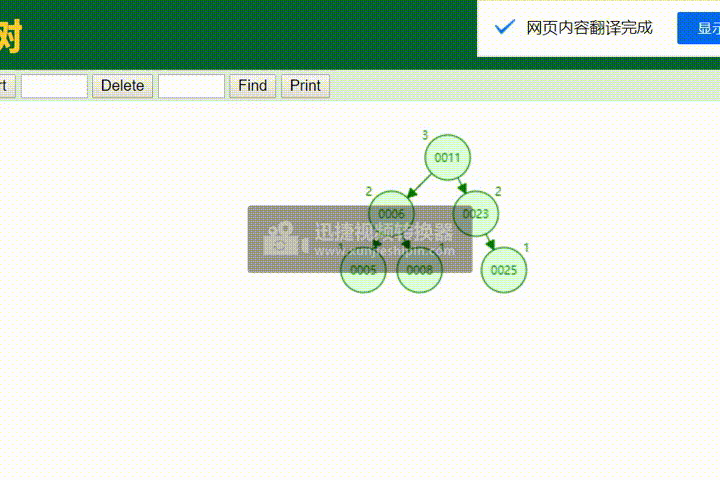
八、测试
将数组中的数插入avl树中
九、完整代码
package lesson9;
import binary.BinarySearch;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
public class AVLtree<T extends Comparable<T>> {
class Node {
T val;
Node left;
Node right;
int heigth; //定义平衡二叉树高度
public Node(T val) {
this.val = val;
this.heigth = 1;
this.left = this.right = null;
}
}
//定义根节点
Node root;
int size;
//构造方法
public AVLtree() {
this.root = null;
this.size = 0;
}
//判断这棵树是否为空
public boolean isEmpty() {
return this.root == null;
}
//获取节点高度
private int getheight(Node node) {
if (node == null) {
return 0;
}
return node.heigth;
}
//获取平衡因子
private int getBalance(Node node) {
if (node == null) {
return 0;
}
return getheight(node.left) - getheight(node.right);
}
//判断是否是二分搜索树
public boolean isBST() {
return isBST(root);
}
//中序遍历的结果进行判断 左 中 右
private boolean isBST(Node node) {
List<T> list = new ArrayList<>();
inorderTraversal(node, list);
for (int i = 0; i < list.size() - 1; i++) {
if (list.get(i).compareTo(list.get(i + 1)) > 0) {
return false;
}
}
return true;
}
//中序遍历
private void inorderTraversal(Node node, List<T> list) {
if (node == null) {
return;
}
inorderTraversal(node.left, list);
list.add(node.val);
inorderTraversal(node.right, list);
}
//3、中序遍历 (按顺序)
public List<String> middleorder() {
List<String> list = new ArrayList<>();
middleorder(root, list);
return list;
}
private void middleorder(Node node, List<String> list) {
//遍历到最后
if (node == null) {
return;
}
//左中右 遍历左边 返回根节点 遍历右边
middleorder(node.left, list);
list.add(node.val + "****************" + getBalance(node));
middleorder(node.right, list);
}
//判断是否是平衡二叉树
public boolean isBalanceTree() {
return isBalanceTree(root);
}
private boolean isBalanceTree(Node node) {
//如果根节点为空,也为平衡树
if (node == null) {
return true;
}
//根节点不为空情况如下 平衡因子的绝对值
int balance = Math.abs(getBalance(node));
if (balance > 1) {
return false;
}
return isBalanceTree(node.left) && isBalanceTree(node.right);
}
//AVL树的右旋 跟节点为x
public Node rightrotate(Node x) {
Node y = x.left;
Node t2 = y.right;
y.right = x;
x.left = t2;
//更新height
x.heigth = Math.max(getheight(x.left), getheight(x.right)) + 1;
y.heigth = Math.max(getheight(y.left), getheight(y.right)) + 1;
return y;
}
//AVL树的左旋
public Node leftrotate(Node x) {
Node y = x.right;
Node t2 = y.left;
y.left = x;
x.right = t2;
//更新height
x.heigth = Math.max(getheight(x.left), getheight(x.right)) + 1;
y.heigth = Math.max(getheight(y.left), getheight(y.right)) + 1;
return y;
}
//1、添加节点
public void add(T ele) {
if (contains(ele) != null) {
return;
}
//利用递归添加节点
root = add(root, ele);
this.size += 1;
}
private Node add(Node node, T ele) {
//如果根节点为空,创建一个新得二叉树,传ele参数进去
if (node == null) {
return new Node(ele);
}
//根节点不为空,将要添加的元素与跟的值进行比较大小
//递归操作 不考虑等于的情况
if (ele.compareTo(node.val) > 0) {
node.right = add(node.right, ele);
} else {
node.left = add(node.left, ele);
}
//更新以node为根的这棵树的高度
node.heigth = Math.max(getheight(node.left), getheight(node.right)) + 1;
//判断是否平衡,不平衡需要作出维护平衡 判断左右旋 还是 右左旋
Node retNode = null;
//右旋
if (getBalance(node) > 1 && getBalance(node.left) >= 0) {
retNode = rightrotate(node);
//左旋
} else if (getBalance(node) < -1 && getBalance(node.right) <= 0) {
retNode = leftrotate(node);
//左右旋
} else if (getBalance(node) > 1 && getBalance(node.left) < 0) {
node.left = leftrotate(node.left);
retNode = rightrotate(node);
//右左旋
} else if (getBalance(node) < -1 && getBalance(node.right) > 0) {
node.right = rightrotate(node.right);
retNode = leftrotate(node);
} else {
retNode = node;
}
return retNode;
}
//2、查询二叉树节点是否包含节点
public Node contains(T ele) {
return contains(root, ele);
}
private Node contains(Node root, T ele) {
if (root == null) {
return null;
}
//递归
T val = root.val;
if (ele.compareTo(val) == 0) {
return root;
} else if (ele.compareTo(val) > 0) {
return contains(root.right, ele);
} else {
return contains(root.left, ele);
}
}
//查找最小元素
public T findminnode() {
if (root == null) {
return null;
}
Node curnode = root; //临时变量指向根节点
while (curnode.left != null) {
curnode = curnode.left;
}
return curnode.val;
}
//5、查找最小元素 递归
public T findminnodeDG() {
if (root == null) {
return null;
}
return findminnodeDG(root).val;//从root节点开始查找最小元素
}
private Node findminnodeDG(Node root) {
if (root.left == null) {
return root;
}
return findminnodeDG(root.left);//向左遍历
}
//删除最小元素
private void removeMixNode() {
//先找到最小节点
T minNodeVal = findminnodeDG();
if (minNodeVal == null) {
System.out.println("isEmpty");
return;
}
System.out.println(minNodeVal.toString());
//进行删除操作
root = removeMixNode(root);
}
private Node removeMixNode(Node node) {
if (node.left == null) {
//进行删除操作
Node rightNode = node.right;
node.right = null;
return rightNode;
}
node.left = removeMixNode(node.left);
return node;
}
//删除任意节点
public T removeNode(T val) {
//判断根是否为0
if (root == null) {
System.out.println("根为0");
return null;
}
//不为零,则需要查找节点
Node node = findNodeDG(root, val);
if (node != null) {
//删除节点
root = removeNode(root, val);
this.size -= 1;
return node.val;
}
return null;
}
/**
* 从以root为根的二分搜索树中删除值为val的节点
*
* @param node
* @param val
* @return
*/
private Node removeNode(Node node, T val) {
Node retNode = null;
//递归到底的情况,找到了删除的节点
//左节点为空,右节点为空,左右节点都为空
if (node.val.compareTo(val) == 0) {
if (node.left == null) {
Node rightNode = node.right;
node.right = null; //删除的为叶子节点
retNode = rightNode;
} else if (node.right == null) {
Node leftNode = node.left;
node.left = null;
retNode= leftNode;
}
else{
//左右节点都不为空
//1、找node 的后继(node.right中的最小节点)
Node t = findminnodeDG(node.right);
//2、node.right 中删除最小节点
// Node node1 = removeMixNode(node.right);
Node rightNodeRoot = removeNode(node.right, t.val); //用递归的方法 删除元素 t.val
//3、使用后继节点替换node
t.left = node.left;
t.right = rightNodeRoot;
//4、生成新树,新树的根节点就是后继节点,返回新树根节点
node.left = node.right = null; //将待删除节点的左右孩子删除 ,断掉关联关系
retNode= t; //返回最终的新节点
}
}else if (node.val.compareTo(val) > 0) {
node.left = removeNode(node.left, val);
retNode =node;
} else {
node.right = removeNode(node.right, val);
retNode = node;
}
//如果待删除的节点为空,返回空,不需要更新树高
if (retNode==null){
return null;
}
//更新以node为根的这棵树的高度
retNode.heigth = Math.max(getheight(node.left), getheight(node.right)) + 1;
Node result = retNode;
//右旋
if (getBalance(retNode) > 1 && getBalance(retNode.left) >= 0) {
result = rightrotate(retNode);
//左旋
} else if (getBalance(retNode) < -1 && getBalance(retNode.right) <= 0) {
result = leftrotate(retNode);
//左右旋
} else if (getBalance(retNode) > 1 && getBalance(retNode.left) < 0) {
retNode.left = leftrotate(retNode.left);
result = rightrotate(retNode);
//右左旋
} else if (getBalance(retNode) < -1 && getBalance(retNode.right) > 0) {
retNode.right = rightrotate(retNode.right);
result = leftrotate(retNode);
}
return result;
}
//查找节点
private Node findNodeDG(Node node, T val) {
//最终没有找到节点,返回null
if (node == null) {
return null;
}
if (node.val.compareTo(val) == 0) {
return node;
} else if (node.val.compareTo(val) > 0) {
return findNodeDG(node.left, val);
} else {
return findNodeDG(node.right, val);
}
}
public int getSize() {
return this.size;
}
@Override
public String toString() {
List<String> list = this.middleorder();
StringBuilder sb = new StringBuilder();
list.forEach(item -> sb.append(item + "\n"));
return sb.toString();
}
}
测试代码
package lesson9;
import java.util.Random;
public class Test {
public static void main(String[] args) {
AVLtree<Integer> AVLtree =new AVLtree();
int[] arr = {23,12,11,5,6,8,25};
for (int i = 0; i <arr.length; i++) {
AVLtree.add(arr[i]);
}
System.out.println(AVLtree.isBST());
System.out.println(AVLtree.isBalanceTree());
System.out.println(AVLtree);
System.out.println("------------------------------------");
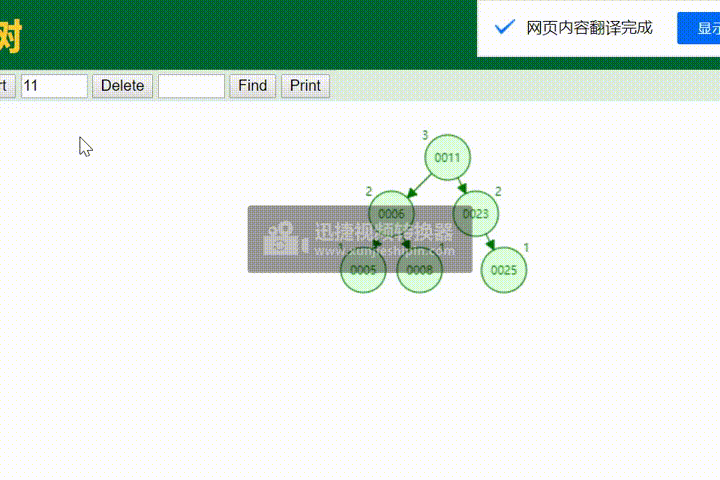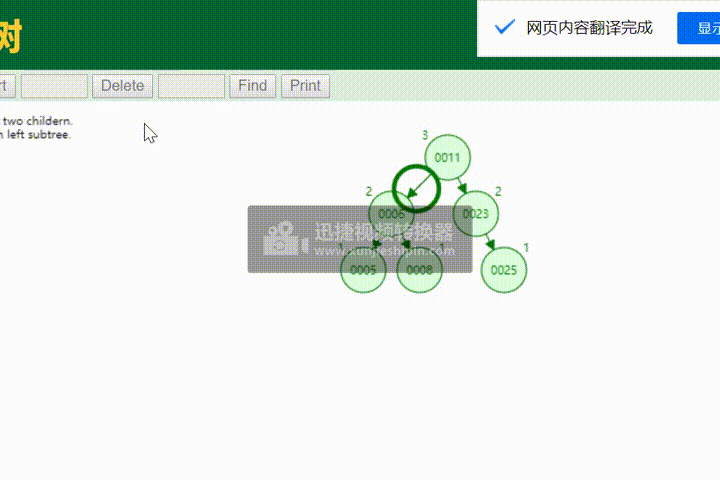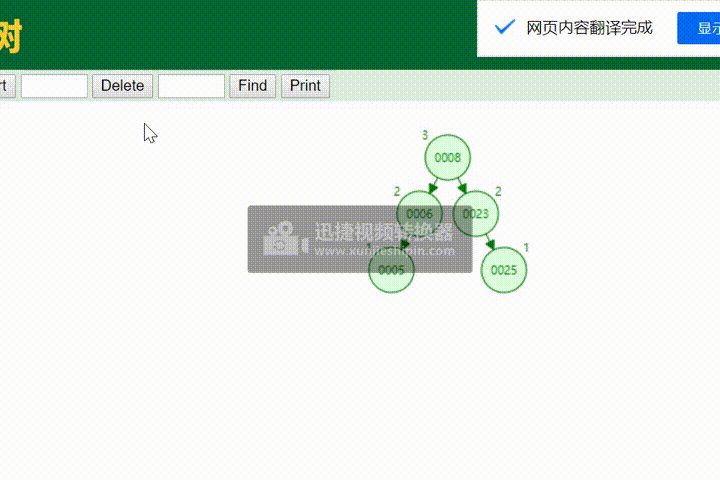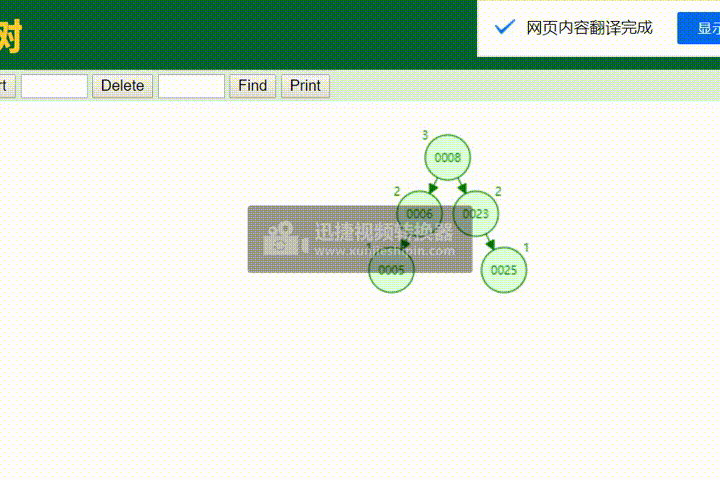
System.out.println("删除的叶子节点为:"+AVLtree.removeNode(12));
System.out.println("删除的跟节点为:"+AVLtree.removeNode(11));
System.out.println(AVLtree.isBST());
System.out.println(AVLtree.isBalanceTree());
System.out.println(AVLtree);
}
}