矩阵最大覆盖问题：最多有多少个矩阵是重合覆盖的

矩阵最大覆盖问题：最多有多少个矩阵是重合覆盖的？

提示：京东原题，根据线段最大重合问题改编而来

极其重要的基础知识：
【1】线段最大重合问题：最多有多少条线段是重合的

---

题目

有一个N*4的二维数组arr，每一个arr[i][0]–arr[i][3]代表一个矩形的左上角坐标，右下角坐标
可能某些矩阵就覆盖重合了，请问你最多有多少个矩阵覆盖重合？

---

一、审题

示例：arr=
1 3 2 1
1 4 4 2
俩矩形就覆盖了重合了，故max=2

---

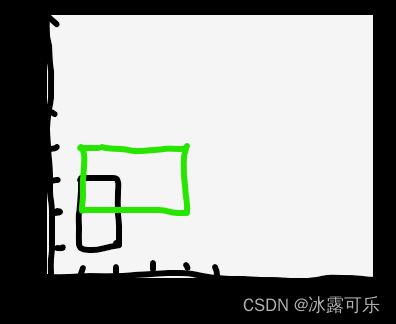
线段最大重合问题

这个题，完全就是下题的改编版本，升级版，京东的原题！
【1】线段最大重合问题：最多有多少条线段是重合的

考虑当前线段cur的start，看看M条线段中，有谁线段x的end会>我线cur的start，统计这个量就是跟我线重合的数量
比如下图粉色线段cur
有绿色的x.end>cur.start
说明有2重合的

---

矩阵最大覆盖问题思想和线段最大重合的思想一样

你看本题前，必须看懂上面那个题目
而本题就是加了上下边的影响

本题的解题思想：
（1）对于一个矩形cur，先看看下面有哪些矩形的上边up，会影响我cur？即x.up>cur.down就是影响我重合的那些矩形【可能哦，x的end不一定影响我的start】，那些x.up<=cur.down的一定不会影响我：
比如下面的x矩形和y矩形，他们的up都大于cur的down，所以可能会影响cur
x的右大于cur的左，肯定x影响cur
但是y的左右，压根不在cur的左右范围内，影响不了，故y不算影响cur

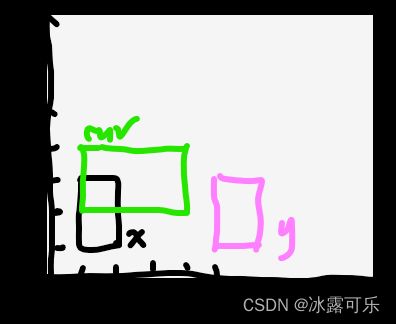
（2）这恰好就引出了（1）的第二步操作，那就是看（1）中收集到的，所有可能影响cur的矩形中，再利用线段最大重合问题找哪些线段影响cur？得到的结果，就是矩形的重合个数。

比如下图xy都是可能的影响cur的矩形，此时我们抛开矩形的上下底，只看矩形的左右start–end
橘色线段代表x矩形，蓝色线段代表y，红色线段代表cur
完全整个矩阵最大覆盖问题就转化为【1】中的线段最大重合问题！
因为x.end>cur.start，所以两者是重合，max=2

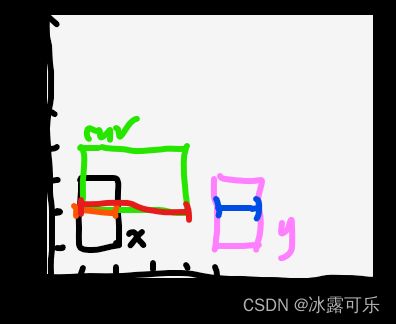
发现了问题的本质了吧，实际上矩阵的重合问题，与【1】中线段重合的区别：就在于先考虑矩阵的上下线段重合问题，再考虑左右线段重合问题

在线段最大重合那，我们先让线段们按照start排序，再让线段们按照end排序
本题中，多了一个比较器，我们先让矩形们按照下底down排序，再让矩形们按照start排序（left），最后再让矩形们按照end排序（right）

逻辑非常清楚了吧！

代码处理流程：
（1）我们统一将给的arr数组转化为特定的数据结构Rectangle
（2）然后准备仨比较器，目的是未来，先让矩形们按照下底down排序，再让矩形们按照start排序（left），最后再让矩形们按照end排序（right）
（3）每一次缩小包围圈的时候，去掉那些不会影响我当前矩形cur的那些矩形，影响我的都加入有序表中。【本题就不再用堆搞了】
——细节上来讲，矩形数组们，按照down排序
——排序好后，从i–N-1所有矩形开始遍历更新答案max，每个矩形cur
前面up够不着我cur.down的全部消除，然后加入能够影响我cur的入有序表setLeft，这个有序表自动按照left边升序排序
——在所有收集好的setLeft中，左边right够不着我cur.left的全部消除，然后加入能够影响我cur的入有序表setRight，这个有效表是自动按照right边升序排序的
——setRight.size()就是与cur能重合的矩形的数量，更新给max

好，下面按照线段最大重合的思路扩展，手撕矩形最大覆盖数的代码：
（1）我们统一将给的arr数组转化为特定的数据结构Rectangle

    //（1）我们统一将给的arr数组转化为特定的数据结构Rectangle
    public static class ReviewRectangle{
        //边
        public int up;
        public int down;
        public int left;
        public int right;
        
        public ReviewRectangle(int l, int u, int r, int d){
            //按照数组直接往里面顺序放左上角，右下角
            left = l;
            up = u;
            right = r;
            down = d;
        }
    }

数组arr，每一个arr[i][0]–arr[i][3]代表一个矩形的左上角坐标，右下角坐标，从0–3顺序放入构造函数就行。

（2）然后准备仨比较器，目的是未来，先让矩形们按照下底down排序，再让矩形们按照start排序（left），最后再让矩形们按照end排序（right）

    //（2）然后准备仨比较器，目的是未来，先让矩形们按照下底down排序，
    // 再让矩形们按照start排序（left），
    // 最后再让矩形们按照end排序（right）
    //先让矩形们按照下底down排序，
    public static class comparatorDown implements Comparator<ReviewRectangle>{
        @Override
        public int compare(ReviewRectangle o1, ReviewRectangle o2){
            return o1.down - o2.down;
        }
    }
    // 再让矩形们按照start排序（left），
    public static class comparatorLeft implements Comparator<ReviewRectangle>{
        @Override
        public int compare(ReviewRectangle o1, ReviewRectangle o2){
            return o1.left - o2.left;
        }
    }
    // 最后再让矩形们按照end排序（right）
    public static class comparatorRight implements Comparator<ReviewRectangle>{
        @Override
        public int compare(ReviewRectangle o1, ReviewRectangle o2){
            return o1.right - o2.right;
        }
    }

（3）每一次缩小包围圈的时候，去掉那些不会影响我当前矩形cur的那些矩形，影响我的都加入有序表中。【本题就不再用堆搞了】
——细节上来讲，矩形数组们，按照down排序
——排序好后，从i–N-1所有矩形开始遍历更新答案max，每个矩形cur
前面up够不着我cur.down的全部消除，然后加入能够影响我cur的入有序表setLeft，这个有序表自动按照left边升序排序
这里要干的事情是：有序表setLeft中前面up够不着我cur.down的全部消除

    //有序表setLeft中删除前面up够不着我cur.down的全部消除
    public static TreeSet<ReviewRectangle> removeRFromSetLeft(TreeSet<ReviewRectangle> setLeft,
                                                              int curDown){
        //查找所有有序表中up<=curDown的，放入要删除的tmp中
        List<ReviewRectangle> tmp = new ArrayList<>();
        for(ReviewRectangle x : setLeft){
            if (x.up <= curDown) tmp.add(x);
        }
        //从setLeft中删除tmp所有元素
        for(ReviewRectangle x : tmp) setLeft.remove(x);//干掉它
        //返回setLeft

        return setLeft;
    }

——在所有收集好的setLeft中，左边right够不着我cur.left的全部消除，然后加入能够影响我cur的入有序表setRight，这个有效表是自动按照right边升序排序的
这里要干的事情是：有序表setRight中,前面right够不着我cur.left的全部消除

    //有序表setRight中,前面right够不着我cur.left的全部消除
    public static TreeSet<ReviewRectangle> removeRFromSetRight(TreeSet<ReviewRectangle> setRight,
                                                              int curLeft){
        //查找所有有序表中right<=curLeft的，放入要删除的tmp中
        List<ReviewRectangle> tmp = new ArrayList<>();
        for(ReviewRectangle x : setRight){
            if (x.right <= curLeft) tmp.add(x);
        }
        //从setRight中删除tmp所有元素
        for(ReviewRectangle x : tmp) setRight.remove(x);//干掉它
        //返回setRight

        return setRight;
    }

——setRight.size()就是与cur能重合的矩形的数量，更新给max

//然后看此时堆中的线段，矩阵个数，就是我当前重合了几个矩形
max = Math.max(max, setRight.size());//与heap.size()一模一样的道理

---

手撕整个矩形最大覆盖问题的代码

总之：本质就在去掉那些不会影响我当前矩形cur的那些矩形，影响我cur矩形的都加入有序表中，有序表的数量就是最大矩阵重合数量。

代码处理流程：
（1）我们统一将给的arr数组转化为特定的数据结构Rectangle
（2）然后准备仨比较器，目的是未来，先让矩形们按照下底down排序，再让矩形们按照start排序（left），最后再让矩形们按照end排序（right）
（3）每一次缩小包围圈的时候，去掉那些不会影响我当前矩形cur的那些矩形，影响我的都加入有序表中。【本题就不再用堆搞了】
——细节上来讲，矩形数组们，按照down排序
——排序好后，从i–N-1所有矩形开始遍历更新答案max，每个矩形cur
前面up够不着我cur.down的全部消除，然后加入能够影响我cur的入有序表setLeft，这个有序表自动按照left边升序排序
——在所有收集好的setLeft中，左边right够不着我cur.left的全部消除，然后加入能够影响我cur的入有序表setRight，这个有效表是自动按照right边升序排序的
——setRight.size()就是与cur能重合的矩形的数量，更新给max

public static int mostNumOfCrossRectangle(int[][] matrix){
        //（1）我们统一将给的arr数组转化为特定的数据结构Rectangle
        if (matrix == null || matrix.length == 0) return 0;
        int N = matrix.length;

        ReviewRectangle[] arr = new ReviewRectangle[N];
        for (int i = 0; i < N; i++) {
            arr[i] = new ReviewRectangle(matrix[i][0], matrix[i][1],
                    matrix[i][2], matrix[i][3]);//左上角，右下角
        }

        //（2）先让矩形们按照下底down排序，
        Arrays.sort(arr, new comparatorDown());

        ——排序好后，从i--N-1所有矩形开始遍历更新答案max，每个矩形cur
        //（3）每一次缩小包围圈的时候，去掉那些不会影响我当前矩形cur的那些矩形，影响我的都加入**有序表**中。
        // 【本题就不再用堆搞了】
        int max = 0;
        TreeSet<ReviewRectangle> setLeft = new TreeSet<>(new comparatorLeft());
        for (int i = 0; i < N; i++) {
            // 再让矩形们按照start排序（left），// 最后再让矩形们按照end排序（right）
            //前面up够不着我cur.down的全部消除，然后加入能够影响我cur的入有序表setLeft，
            // 这个有序表自动按照left边升序排序
            int curDown = arr[i].down;
            removeRFromSetLeft(setLeft, curDown);
            //考虑到curDown相等的可能不少，就一气呵成加入setLeft
            int index = i;//从i--后面一堆同样的curDown
            while (index < N && curDown == arr[index].down) {
                setLeft.add(arr[index]);
                index++;
            }
            //加完把坐标换成当前index，它的down与curDown不一样哦！！！
            i = index - 1;//这样的话，下一个fori就从那最新的index开始,对于fori来说i还会++，提前把index-1

            //——在所有收集好的setLeft中，每个矩阵i，都会有自己的setRight
            TreeSet<ReviewRectangle> setRight = new TreeSet<>(new comparatorRight());
            for(ReviewRectangle cur : setLeft){
                //左边right够不着我cur.left的全部消除，
                int curLeft = cur.left;
                removeRFromSetRight(setRight, curLeft);
                // 然后加入能够影响我cur的入有序表setRight，这个有效表是自动按照right边升序排序的
                //这就没法找相等的左边了，一个个比就行
                setRight.add(cur);

                //——setRight.size()就是与cur能重合的矩形的数量，更新给max
                max = Math.max(max, setRight.size());
            }
        }

        return max;
    }

注意代码中，index加到下一个不等于curDown时，不加了，下次就该考虑index位置整个矩阵，
如果你恢复为i=index，fori循环还会i++，i就多加了1，相等于i=index+1了，这是不行的，所以要提前把index减1，即i=index-1；
这样fori循环还会i++，i=index-1+1=index；

测试一下：

    public static void test(){
        //给一个非标准的数组
        int[][] recArr = {
                {3,7,5,2},
                {4,8,6,3},
                {1,8,7,4}
        };//重合了3个
        //左上角，右下角，left，up，right，down
        //然后我们转成标准的矩形数据结构
        Rectangle[] recs = normalArrToRectangle(recArr);
        //转换好了才能去求最大的重合数量
        System.out.println(getMaxCoverRectangleNum(recs));

        System.out.println(mostNumOfCrossRectangle(recArr));//我这个更牛，内部转换
    }

    public static void main(String[] args) {
        test();
    }

3
3

问题不大

---

总结

提示：重要经验：

1）线段最大重合问题，是矩阵最大覆盖问题的根基，一定要把线段最大重合问题那个题搞透彻，才能理解本题
2）本题本质就在去掉那些不会影响我当前矩形cur的那些矩形，影响我cur矩形的都加入有序表中，有序表的数量就是最大矩阵重合数量。
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。