【读书笔记】《算法竞赛进阶指南》读书笔记——0x10基本数据结构

to do(perhaps never)

CH1401 后缀数组
所有课后题

---

栈

例题：HDU4699 Editor

维护一个整数序列的编辑器，支持以下五种操作：
I x：在当前光标位置处插入一个整数x，插入后光标移动到x之后
D：删除光标之前的一个元素，相当于按下退格键
L：光标左移一个位置，相当于按下左方向键
R：光标右移一个位置，相当于按下右方向键
Q k：在位置k之前最大的前缀和，k不超过光标当前的位置

建立两个栈，栈A储存从开头到光标之前的元素，栈B储存光标之后到序列结束的元素，设栈A栈顶元素的下标是$p_A$，sum是序列A的前缀和数组，f数组维护A的最大前缀和。

对于I x：

1. 将x插入栈A；
2. 更新$sum[p_A]=sum[p_A-1]+A[p_A]$；
3. 更新$f[p_A]=max(f[p_A-1],sum[p_A])$；

对于D：
弹出A栈顶的元素；

对于L：弹出A的栈顶，插入B；

对于R操作：

1. 弹出B的栈顶，插入A；
2. 更新$sum[p_A]=sum[p_A-1]+A[p_A]$；
3. 更新$f[p_A]=max(f[p_A-1],sum[p_A])$；

对于Q k操作：
返回$f[k]$；

多组样例输入，并且记得关流，998ms。

int sum[1000000 + 5], ans[1000000 + 5] = { (int)-1e9 }, n;

int main()
{
    while (cin >> n)
    {
        stack <int> a, b;

        while (n--)
        {
            char op;
            int tmp;
            cin >> op;

            if (op == 'I')
            {
                cin >> tmp;

                a.push(tmp);
                int len = a.size();

                sum[len] = sum[len - 1] + tmp;
                ans[len] = max(ans[len - 1], sum[len]);
            }
            else if (op == 'D')
            {
                if (!a.empty()) a.pop();
            }
            else if (op == 'L')
            {
                if (!a.empty())
                {
                    b.push(a.top());
                    a.pop();
                }
            }
            else if (op == 'R')
            {
                if (!b.empty())
                {
                    a.push(b.top());
                    b.pop();

                    int len = a.size();
                    sum[len] = sum[len - 1] + a.top();
                    ans[len] = max(ans[len - 1], sum[len]);
                }
            }
            else if (op == 'Q')
            {
                cin >> tmp;
                cout << ans[tmp] << endl;
            }
        }
    }
}

例题：CH1101/1102 火车进出站问题

给定1~N这N个整数和一个无限大的栈，每个数都要进栈并且出栈一次，如果进栈的顺序为1，2，……，N，那么可能的出栈顺序有多少种。

方法一：搜索（枚举/递归）$\Theta (2^N)$

面对任何一个状态，我们只有两种选择：

1. 把下一个数进栈；
2. 栈顶的数出栈

方法二：递推$\Theta (N^2)$

如果只要求方案数，不需要具体的方案，可以使用递推直接统计：
设$S_N$表示进栈顺序为$1,2,\cdots ,N$时可能的出栈顺序总数，现在考虑数字1在出栈顺序中的位置，如果1排在第k个出栈，那么整个进出栈的过程为：

1. 整数1进栈；
2. 2 ~ k - 1这k - 2个数以某种顺序进出栈；
3. 整数1出栈，排在第k个；
4. k + 1 ~ N 这N - k个数字按照某种顺序进出栈；

于是可以得到递推公式：

$$S_N=\sum _{k=1}^N{S}_{k-1}\ast S_{N-k}$$

方法三：动态规划$\Theta (N^2)$

用$F[i,j]$表示有i个数尚未进栈，目前有j个数在栈中，有n - i - j个数已经出栈时的方案总数，边界条件：$开始：F[0,0]=1结束：F[N,0]$；
由于每一步只能执行两种操作：把一个数进栈和把一个数出栈，所以递推公式为：
$$F[i,j]=F[i-1,j+1]+F[i,j-1]$$

方法四：数学$\Theta (N)$

该问题等价于求第N项Catalan数，即$C_{2N}^N/(N+1)$，将在第三章介绍。

CH1101火车进站
摸鱼一个寒假递归都快不会写了~~~

int n, cnt;

void solve(int train, stack <int> s, vector <int> ans)
{
    if (cnt >= 20)
    {
        return;
    }
    else if (train > n)
    {
        cnt++;
        for (auto i : ans)
        {
            cout << i;
        }
        while (!s.empty())
        {
            cout << s.top();
            s.pop();
        }
        cout << endl;
    }
    else
    {
        int tmp;
        if (!s.empty())
        {
            tmp =  s.top();
            ans.push_back(tmp);
            s.pop();
            solve(train, s, ans);
            ans.pop_back();
            s.push(tmp);
        }

        s.push(train);
        solve(train + 1, s, ans);
    }
}

int main()
{
    while (cin >> n)
    {
        cnt = 0;
        stack <int> s;
        vector <int> ans;
        solve(1, s, ans);
    }
}

CH1102火车进出栈问题

不会大数→_→，copy

const int MAX = 6e4 + 5, HEX = 1e9;
int a[MAX], b[MAX], di[MAX * 2 + 5], n;//a = (n + 1)...2n, b = (n + 1)!

deque<int> operator*(const deque<int> &op1, int op2) {
    deque<int> res;
    int carry = 0;
    for (long long i = op1.size() - 1, tmp; i >= 0; --i)
        tmp = (long long) op1[i] * op2 + carry, res.push_front(tmp % HEX), carry = tmp / HEX;
    if (carry) res.push_front(carry);
    return res;
}

//将arr[l...r]分解质因数到di, k为1或-1,div[i](i为素数)将a/b分解质因数后i的次幂
void resolve(int *arr, int l, int r, int k) {
    for (int i = l; i <= r; ++i) {
        for (int j = 2; j * j <= arr[i]; ++j) if (!(arr[i] % j)) arr[i] /= j, di[j] += k, --j;
        if (arr[i] > 1) di[arr[i]] += k;
    }
}

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n + 1; ++i) a[i] = n + i, b[i] = i;
    resolve(a, 1, n, 1), resolve(b, 1, n + 1, -1);
    deque<int> res(1, 1);
    for (int i = 1; i <= n << 1; ++i) for (int j = 1; j <= di[i]; ++j) res = res * i;
    printf("%d", res[0]);
    for (int i = 1; i < res.size(); ++i) printf("%09d", res[i]);
}

表达式的计算

中缀表达式：最常见的表达式，如$3\ast (1-2)$
前缀表达式：又称波兰式，例如$\ast 3-12$
后缀表达式：又称逆波兰式，例如$12-3\ast$

后缀表达式可以在$\Theta (N)$的时间内求值。

后缀表达式求值方式：
建立一个栈，从左往右扫描表达式：

1. 遇到数字，入栈
2. 遇到运算符，弹出栈中的两个元素，计算结果后再将结果压入栈
   扫描完成之后，栈中只剩下一个数字，最终结果。

中缀表达式转后缀表达式：

1. 建立一个用于储存运算符的栈，逐一扫描中缀表达式中的元素
   1. 扫描到数字，输出该数；
   2. 遇到左括号，将左括号入栈；
   3. 遇到右括号，不断取出栈顶元素并且输出，直到栈顶为左括号，并弹出左括号舍弃
   4. 遇到运算符，如果栈顶的运算符优先级大于当前扫描到的运算符，就不断取出栈顶的元素，最后将新符号入栈；
2. 将栈中剩余的运算符输出，所有的输出结果即为转化后的后缀表达式。

单调栈

例题：POJ2559 Largest Rectangle in a Histogram

妙啊！！！

建立一个栈，从左往右扫描题目给的举行序列；

如果当前扫描到的矩形比栈顶的矩形高，直接进栈；

否则，不断取出栈顶的元素，直到栈为空或者栈顶的矩形比当前矩形矮；出栈的过程中，累计被弹出的矩形的宽度之和，并且每弹出一个矩形，就用它的高度乘上累计的宽度更新答案，出栈过程结束后，我们把一个高为当前矩形高度，宽度为累计的宽度的矩形入栈。

扫描过程结束之后，将栈中剩余的矩形以此出栈，用上面的方法更新答案，为了简化流程，也可以手动添加一个高度为0的矩形，以免扫描结束后栈中还有剩余的矩形。

书本代码：

a[n + 1] = p = 0;
for (int i = 1; i <= n + 1; ++i)
{
    if (a[i] > s[p])
    {
        s[++p] = a[i];
        w[p] = 1;
    }
    else 
    {
        int width = 0;
        while (s[p] > a[i])
        {
            width += w[p];
            ans = max(ans, width * s[p]);
            p--;
        }
        s[++p] = a[i];
        w[p] = width + 1;
    }
}

自己敲的：：
正好赶上POJ歇菜，在CH上交了，只有一组数据？？？

typedef long long ll;

struct rect
{
    ll width, height;
    rect(ll w, ll h) : width(w), height(h) {}
};

int main()
{
    cin.sync_with_stdio(false);
    cin.tie(0);

    int n;
    while (cin >> n && n)
    {
        vector <rect> arr;
        stack <rect> s;
        while (n--)
        {
            ll tmp;
            cin >> tmp;
            arr.push_back(rect(1, tmp));
        }
        arr.push_back(rect(1, 0));

        ll ans = 0;
        for (vector <rect>::iterator i = arr.begin(); i != arr.end(); ++i)
        {
            rect now = *i;

            if (s.empty() || s.top().height < now.height)
            {
                s.push(now);
            }
            else
            {
                ll width = 0;
                while (!s.empty() && s.top().height >= now.height)
                {
                    rect tmp = s.top(); s.pop();

                    width += tmp.width;
                    ans = max(ans, width * tmp.height);
                }
                s.push(rect(now.width + width, now.height));
            }
        }

        cout << ans << endl;
    }
}

---

队列

例题：POJ2259 Team Queue

n个小组进行排队，每个小组由若干人，当一个人来到队伍时，如果队伍中已有自己小组的成员，则排在自己小组成员的后面，如果没有自己小组的成员，则排在队伍末尾，给出一系列出队、入队指令，输出出队顺序。

建立一个队列$Q_0$，储存小组的编号，然后为每一个小组建立一个队列$Q_i$，一共n+1个队列；当一个编号为X，组号为Y的的人来到队伍时，先将其插入到$Q_Y$末尾，如果之前$Q_Y$是空的，还要将$Y$插入到$Q_0$末尾。

当需要出队时，先通过$Q_0$找到对手的队伍，在弹出相应队伍的第一个人，如果弹出后这个队伍变为空，再弹出$Q_0$队首的元素。

int team[1000010], n;
queue <int> q0, qs[1010];

int main()
{
    int cnt = 1;
    while (cin >> n && n)
    {
        cout << "Scenario #" << cnt << endl; cnt++;

        for (int i = 0; i < n; ++i)
        {
            int num, t;
            cin >> num;
            while (num--)
            {
                cin >> t;
                team[t] = i;
            }
        }

        string s;
        while (cin >> s)
        {
            if (s == "STOP")
            {
                break;
            }
            else if (s == "ENQUEUE")
            {
                int t;
                cin >> t;
                int fa = team[t];

                if (qs[fa].empty()) q0.push(fa);
                qs[fa].push(t);
            }
            else
            {
                int t = q0.front();
                cout << qs[t].front() << endl;
                qs[t].pop();
                if (qs[t].empty()) q0.pop();
            }
        }
        cout << endl;

        while (!q0.empty()) q0.pop();
        for (int i = 0; i < n; ++i)
        {
            while (!qs[i].empty())
                qs[i].pop();
        }
    }
}

例题：双端队列

对N个数进行排序，只能进行利用双端队列，只能进行如下几种操作：

1. 新建一个双端队列，把这个数字作为队列中唯一的数字；
2. 将当前数字放入已有的队列的队首或者队尾；

在所有的数字处理完之后，要求所有的队列能按照一定顺序连接起来得到一个非降序列，求解最少需要几个双端队列。
与数据结构关系不大，仅供思维训练

反过来思考，先将所有数字非降序排序，然后分成尽量少的几段，让每一段刚好对应一个双端队列。

以样例为例：
输入数据：$[3,6,0,9,6,3]$，下标分别为：$[1,2,3,4,5,6]$。
排序后得到：$[0,3,3,6,6,9]$，下标分别为：$[3,1,6,2,5,4]$。

经过观察可以发现，如果排序后的下表满足单谷性质，那么这一段就可以对应一个双端队列，递减的一段相当于从队首插入，递增的一段相当于从队尾插入。

还需要注意的是，输入数据中有相等的数，可以任意交换顺序。

struct node
{
    int val, pos;
    friend bool operator<(node a, node b)
    {
        return a.val < b.val || (a.val == b.val && a.pos < b.pos);
    }
}
arr[200100 * 2];

int n, from[200100],to[200100], cnt, ans, now = 1 << 30;
bool flag = true;

int main()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
    {
        cin >> arr[i].val;
        arr[i].pos = i;
    }

    sort(arr + 1, arr + 1 + n);

    for (int i = 1; i <= n; ++i)
    {
        if (i == 1 || arr[i].val != arr[i - 1].val)
        {
            from[cnt] = arr[i - 1].pos;
            to[++cnt] = arr[i].pos; // 分段
        }
    }

    from[cnt] = arr[n].pos;
    for (int i = 1; i <= cnt; ++i)
    {
        if (flag)
        {
            if (now < to[i])
                now = from[i];
            else
            {
                flag = false;
                now = to[i];
                ans++;
            }
        }
        else
        {
            if (now > from[i])
                now = to[i];
            else
            {
                now = from[i];
                flag = true;
            }
        }
    }

    cout << ans << endl;
}

单调队列

例题：CH1201 最大子序和

给定一个长度为N的整数序列（存在负数），求一个长度不超过M的子序列，使这个子序列中所有数的和最大。

以$S[i]$表示原序列前i个数字的和，枚举右端点i，问题变为找到一个左端点j，其中$j\in [i-m,i-1]$，并且s[j]最小。

可能成为最优选择的j的集合一定是一个下标递增，前缀和也递增的序列，可以用一个双端队列记录这个序列。

随着右端点从前往后扫描，进行如下操作：

1. 在队首弹出所有距离超过M的点。
2. 此时的队首元素就是最佳选择。
3. 在队尾弹出所有值大于等于当前右端点值的点，然后将右端点从队尾入队。

（经过上面的操作，双端队列里的元素是升序的，自己模拟一下就知道了）

由于每一个点只会入队一次，所以时间复杂度为$\Theta (N)$。
单调队列是动态优化的重要手段，将在之后的章节更详细的讲解。

int sum[300000 + 5], n, m;

int main()
{
    while (cin >> n >> m)
    {
        for (int i = 1; i <= n; ++i)
        {
            int t;
            cin >> t;
            sum[i] = t + sum[i - 1];
        }

        deque <int> q;
        q.push_back(1);

        int ans = sum[1];
        for (int i = 2; i <= n; ++i)
        {
            while (!q.empty() && i - q.front() > m)
                q.pop_front();

            ans = max(ans, sum[i] - sum[q.front()]);

            while (!q.empty() && sum[q.back()] >= sum[i])
                q.pop_back();

            q.push_back(i);
        }

        cout << ans << endl;
    }
}

---

链表与邻接表

两种链表模板：

动态内存、指针：

struct node
{
    int val;
    node *pre, *nex;
};
node *head, *tail;

void init()
{
    head = new node();
    tail = new node();
    head->nex = tail;
    tail->pre = head;
}

void insert(node* p, int val) // 在p后面插入
{
    node* tmp = new node();
    tmp->val = val;

    p->nex->pre = tmp;
    tmp->nex = p->nex;
    p->nex = tmp;
    tmp->pre = p;
}

void remove(node* p) // 删除节点
{
    p->pre->nex = p->nex;
    p->nex->pre = p->pre;
    delete p;
}

void recycle() // 回收整个链表
{
    while (head != tail)
    {
        head = head->nex;
        delete head->pre;
    }
    delete tail;
}

数组模拟：

struct node
{
    int val;
    int pre, nex;
} List[SIZE];

int head, tail, cnt;

void init()
{
    cnt = 2;
    head = 1, tail = 2;
    List[head].nex = tail;
    List[tail].pre = head;
}

void insert(int p, int val)
{
    cnt++;
    int tmp = cnt;

    List[tmp].val = val;
    List[List[p].nex].pre = tmp;
    List[tmp].nex = List[p].nex;
    List[p].nex =tmp;
    List[tmp].pre = p;
}

void remove(int p)
{
    List[List[p].pre].nex = List[p].nex;
    List[List[p].nex].pre = List[p].pre;
}

例题：CH1301 邻值查找

给定一个长度为n的序列A，A中的数字各不相同，对于其中的每一个数字$A_i$，求$min\left|A_i-A_j\right|$并记录j，如有多个解，选择$A_j$最小的。

解法一：平衡树（STL set）：

由于set是平衡树，所以当前新插入的节点之前和之后的节点刚好是比当前节点值小的节点中最大的、比当前节点值大的节点中最小的，只要考虑这两个点即可。

struct Node
{
    int index, val;

    Node(int i, int v) : index(i), val(v) {}

    friend bool operator<(Node a, Node b)
    {
        return a.val < b.val;
    }
};

int arr[100000 + 10], n;

bool cmp(int a, int b, int c)
{
    return abs(a - c) < abs(b - c) || \
    (abs(a - c) == abs(b - c) && a < b);
}

int main()
{
    while (cin >> n)
    {
        for (int i = 0; i < n; ++i) cin >> arr[i];

        set <Node> s;
        set <Node>::iterator now, pre, nex;

        for (int i = 0; i < n; ++i)
        {
            Node node(i, arr[i]);

            s.insert(node);
            now = s.find(node);

            pre = nex = now;
            nex++;

            int v[3], cnt = 0, ans;
            if (pre != s.begin())
            {
                pre--;
                v[cnt] = pre->index;
                ++cnt;
            }
            if (nex != s.end())
            {
                v[cnt] = nex->index;
                ++cnt;
            }


            if (i)
            {
                if (cnt < 2 || cmp(arr[v[0]], arr[v[1]], arr[i]))
                    ans = v[0];
                else
                    ans = v[1];

                cout << abs(arr[i] - arr[ans]) << " " << ans + 1 << endl;
            }
        }
    }
}

方法二：链表：

将序列A从小到大排序，然后依次串成一个链表，同时建立一个数组B，其中$B_i$表示原始序列中$A_i$的位置（指针）。

这样一来，指针$B_n$指向的节点的前驱和后继就是原始序列中值和$A_n$最相近的两个元素，即可以计算出$A_n$对应的答案。

接下来，在链表中删除$B_n$指向的元素，然后用同样的方法操作$B_{n-1}$，如此往复。

注意理解流程。

思考了一下这个方法用数组模拟链表更方便，已使用书本的链表模板。

struct node
{
    int val, index;

    friend bool operator<(node a, node b)
    {
        return a.val < b.val;
    }
}
arr[100000 + 5];

struct ListNode
{
    node elem;
    int pre, nex;
} List[100000 + 5];

int head, tail, cnt, n, ptr[100000 + 5], res[100000 + 5][2];

void init()
{
    cnt = 1;
    head = 1, tail = 0;
    List[head].nex = tail;
    List[tail].pre = head;
}

void insert(int p, node val)
{
    cnt++;
    int tmp = cnt;

    List[tmp].elem = val;
    List[List[p].nex].pre = tmp;
    List[tmp].nex = List[p].nex;
    List[p].nex =tmp;
    List[tmp].pre = p;
}

void remove(int p)
{
    List[List[p].pre].nex = List[p].nex;
    List[List[p].nex].pre = List[p].pre;
}

bool cmp(int a, int b, int c)
{
    return abs(a - c) < abs(b - c) || \
    (abs(a - c) == abs(b - c) && a < b);
}

int main()
{
    while (cin >> n)
    {
        for (int i = 0; i < n; ++i)
        {
            cin >> arr[i].val;
            arr[i].index = i;
        }

        sort(arr, arr + n);
        init();

        for (int i = 0; i < n; ++i)
        {
            insert(cnt, arr[i]);
            ptr[arr[i].index] = cnt;
        }

        for (int i = n - 1; i >= 0; --i)
        {
            int now = ptr[i];
            int pre = List[now].pre;
            int nex = List[now].nex;

            node v[3], ans;
            int cnt = 0;

            if (pre != head)
            {
                v[cnt] = List[pre].elem;
                ++cnt;
            }
            if (nex != tail)
            {
                v[cnt] = List[nex].elem;
                ++cnt;
            }

            if (cnt)
            {
                if (cnt < 2 || cmp(v[0].val, v[1].val, List[now].elem.val))
                {
                    ans = v[0];
                }
                else
                {
                    ans = v[1];
                }
                res[i][0] = abs(ans.val - List[now].elem.val);
                res[i][1] = ans.index + 1;
            }
            remove(now);
        }

        for (int i = 1; i < n; ++i)
        {
            cout << res[i][0] << " " << res[i][1] << endl;
        }
    }
}

又是这道例题：POJ3784 Running Median

先将整个序列读入，排序之后依次插入一个链表，此时我们可以知道整个序列的中位数，随后，按照读入的倒序，一个一个删除链表中的元素。

懒，不写了(～o￣3￣)～

邻接表

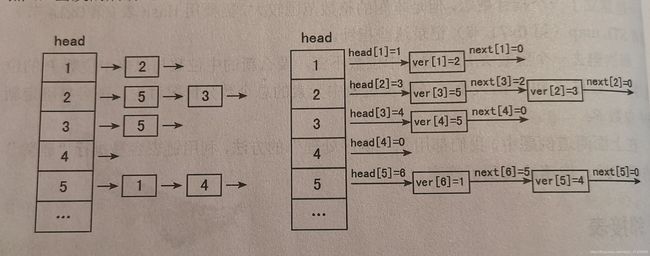
图片表示一张5个点，6条边的图，边按插入顺序为：(1, 2),(2, 3),(2, 5),(3, 5),(5, 4),(5, 1)。

ver数组储存终点，edge数组储存权值，next数组储存每一条边的下一条边head储存以某一个点为起点的第一个点，head与next储存的都是ver的下表。

void add(int from, int to, int weight)
{
    cnt++;
    ver[cnt] = to;
    edge[cnt] = weight;
    next[cnt] = head[from];
    head[from] = cnt; 
    // 在链表开头插入，每一个链表代表从某一点开始所有能到达的点
}

// 访问从x出发的所有边
for (int i = head[x]; i != 0; i = next[i])
{
    int from = x;
    int to = ver[i];
    int weight = edge[i];
    // 进行操作
}

---

Hash

Hash表又称散列表，一般由Hash函数与链表结构共同实现。

有一种称为开散列的解决方案是，建立一个邻接表结构，以Hash函数的值域作为表头数组，映射后的值相同的原始信息被分到同一类。

例如，统计一个长度为N的随机数序列A中每一个数字分别出现了多少次，设计Hash函数为$H(x)=(xmodP)+1$，P为一个比较大的质数，显然，这个Hash函数将序列A分为P类，对于每一个A[i]，定位到head[H(A[i])]指向的表头，如果链表中不包含A[i]，插入新节点，如果已经存在，出现次数累加1，由于是随机数A[i]会均匀分散在每一个表头，整体的时间复杂度为$\Theta (N)$。

例题：POJ3349 Snowflake

每个雪花有六个角，长度分别为$a_1,a_2,\cdots ,a_6$，从任意一个角开始逆时针或顺时针记录长度得到的六元组都代表此种形状的雪花；
给定N片雪花，求是否存在两片相同的雪花。

Hash函数：

$$H(a_1,a_2,\cdots ,a_6)=(\sum _{i=1}^6{a}_i+\prod _{i=1}^6{a}_i)modP，P为一个较大的质数$$

相同的雪花，计算出的hash值一定相同；每加入一片新雪花，在hash值相同的已有雪花中寻找是否有相同的，如果有，返回结果，如果没有，将此片雪花插入。

本人用了一套繁琐的map+vector+struct。。。

using ll = long long;
constexpr ll p = 99991;

ll HASH(const ll arr[])
{
    ll sum = 0, prod = 1;
    for (int i = 0; i < 6; ++i)
    {
        sum = (sum + arr[i]) % p;
        prod = (prod * arr[i]) % p;
    }
    return (sum + prod) % p;
}

bool isEqual(ll a[], ll b[])
{
    for (int i = 0; i < 6; ++i)
    {
        for (int j = 0; j < 6; ++j)
        {
            bool ans = true;
            for (int k = 0; k < 6; ++k)
            {
                if (a[(i + k) % 6] != b[(j + k) % 6])
                {
                    ans = false;
                    break;
                }
            }

            if (ans) return true;
            ans = true;

            for (int k = 0; k < 6; ++k)
            {
                if (a[(i + k) % 6] != b[(j - k + 6) % 6])
                {
                    ans = false;
                    break;
                }
            }
            if (ans) return true;
        }
    }
    return false;
}

struct snow
{
    ll arr[6];
};

int main()
{
    ll n, arr[6];
    map <ll, vector <snow> > mp;

    cin >> n;
    while (n--)
    {
        for (auto& i : arr) cin >> i;
        ll h = HASH(arr);

        auto& vec = mp[h];
        for (auto& i : vec)
        {
            if (isEqual(i.arr, arr))
            {
                cout << "Twin snowflakes found." << endl;
                return 0;
            }
        }

        snow s;
        for (int i = 0; i < 6; ++i) s.arr[i] = arr[i];
        mp[h].emplace_back(s);
    }

    cout << "No two snowflakes are alike." << endl;
}

字符串Hash

将一个任意长度的字符串映射为一个非负整数，并且其冲突概率几乎为零。

取一个固定值P，将字符串看作P进制数，并为每一个字符分配一个大于0的数值，例如对于小写字母，令$a=1,b=2,c=3,\cdots ,z=26$，取一个固定值M，求出该P进制数对M的余数，作为该字符串的Hash值。

一般来说，我们取$P=131或13331$，此时Hash值冲突的概率极低；同时，取$M=2^{64}$，用unsigned long long储存Hash值，这样的话算术溢出就相当于取模。

除非特殊构造的数据，上述Hash算法很难冲突；保险起见，可以多取几组P和M（例如大质数），多进行几组Hash运算，结果都相等时才认为字符串相等

对字符串的各种操作，都可以直接对P进制数进行操作反映到Hash值上：

已知字符串S的Hash值是$H(S)$，那么在S后面添加一个字符c之后新的字符串的Hash值为$H(S+c)=(H(s)\ast P+value[c])modM$。

已知字符串S的Hash值为$H(S)$，字符串S+T的Hash值为$H(S+T)$，那么T的Hash值就是：$H(T)=(H(S+T)-H(S)\ast P^{length(T)})modM$。

通过上面的操作，我们就可以在$\Theta (N)$的时间内与处理所有字符串的Hash值，并在$\Theta (1)$的时间内查询任意字串的Hash值。

例题：CH1401 兔子与兔子

先给定一个很长很长的字符串，然后问你里面的两个字符串是否完全相等。

设原字符串为S[]，数组F[i]表示子串S[1~i]的Hash值，取P=131，于是有递推公式：$F[i]=F[i-1]\ast P+value[S[i]]$，任意一个区间$[l,r]$Hash值的计算公式为：$F[r]-F[l-1]\ast P^{r-l+1}$。

using ull = unsigned long long;

ull f[1000000 + 10], p[1000000 + 10], n, l1, r1, l2, r2;

int main()
{
    string s;
    cin >> s >> n;

    p[0] = 1;
    for (int i = 1; i <= s.length(); ++i)
    {
        p[i] = p[i - 1] * 131;
        f[i] = f[i - 1] * 131 + s[i - 1] - 'a' + 1;
    }

    while (n--)
    {
        cin >> l1 >> r1 >> l2 >> r2;
        ull dna1 = f[r1] - f[l1 - 1] * p[r1 - l1 + 1];
        ull dna2 = f[r2] - f[l2 - 1] * p[r2 - l2 + 1];

        if (dna1 == dna2) cout << "Yes" << endl;
        else cout << "No" << endl;
    }
}

例题：POJ3974 Palindrome

给定一个字符串，求最长回文子串。

枚举回文串中心的位置，$i=[1,N]$，检查从中心往外左右两侧最长可以扩展到多长：

1. 求出一个最大的数p使得$S[i-p,i]=reverse(S[i,i+p])$，那么此回文串长度为$2\ast p+1$。

2. 求出一个最大的数q使得$S[i-q,i-1]==reverse(S[i,i+q-1])$，那么此回文串的长度为$2\ast q$。

根据上一道题目，我们已经知道如何通过$\Theta (N)$的预处理使得可以在$\Theta (1)$的时间内计算原字符串任意字串的Hash值；类似的，对原字符串倒着进行一遍处理，就能在$\Theta (1)$的时间内计算原字符串任意字串的逆序的Hash值。

对于每一个位置i，可以使用二分的方法在$\Theta (\log N)$的时间内找到p、q的位置；于是，本解法的总时间复杂度为$\Theta (N\log N)$。

Manacher算法日后介绍。$\Theta (N)$时间复杂度。

typedef unsigned long long ull;

const int MAXN = 1000007;
char s[MAXN];
ull f1[MAXN], f2[MAXN], p[MAXN];

inline ull H(int i, int j)
{
	return (f1[j] - f1[i - 1] * p[j - i + 1]);
}

inline ull H2(int i, int j)
{
	return (f2[i] - f2[j + 1] * p[j - i + 1]);
}

int main()
{
	int ans = 0, cases = 0;
	p[0] = 1;

	for (int i = 1; i < MAXN; ++i)
		p[i] = p[i - 1] * 131;

	while (1)
	{
		++cases;
		ans = 0;

		scanf("%s", s + 1);
		int L = strlen(s + 1);

		if (L == 3 && s[1] == 'E' && s[2] == 'N' && s[3] == 'D')
			break;

		f2[L + 1] = 0;

		for (int i = 1; i <= L; ++i)
			f1[i] = f1[i - 1] * 131 + s[i] - 'a' + 1;

		for (int i = L; i >= 1; --i)
			f2[i] = f2[i + 1] * 131 + s[i] - 'a' + 1;

		for (int pos = 1; pos <= L; ++pos)
		{
			int l = 1, r = min(pos - 1, L - pos), mid;

			while (l < r)
			{
				mid = (l + r + 1) >> 1;
				if (H(pos - mid, pos - 1) == H2(pos + 1, pos + mid))
				{
					l = mid;
				}
				else
				{
					r = mid - 1;
				}
			}

			ans = max(l * 2 + 1, ans);

			l = 1, r = min(pos - 1, L - pos + 1);

			while (l < r)
			{
				mid = (l + r + 1) >> 1;
				if (H(pos - mid, pos - 1) == H2(pos, pos + mid - 1))
				{
					l = mid;
				}
				else
				{
					r = mid - 1;
				}
			}

			ans = max(l * 2, ans);
		}
		
		printf("Case %d: %d\n", cases, ans);
	}
	return 0;
}

例题：CH1402 后缀数组（Suffix Array）

留坑，Mark

---

字符串

KMP模式匹配

KMP算法，又称模式匹配算法，能够在线性时间内判断一个字符串是否为另一个字符串的子串，并以此求出子串的出现位置。

KMP算法分为两步：

2019-3-21改动，原本这里我写的A是主串，B是子串，zz了···

设A[1 ~ N]为子串，B[1 ~ M]为主串；

1. 对字符串A进行自我“匹配”，即求出一个数组$next[]$，其中$next[i]$表示A中以i结尾的非前缀子串与A的前缀能够匹配的最长长度，即：$next[i]=max\{j\}，其中j<i且A[1:j]=A[i-j+1:i]$当这样的j不存在时，令$next[i]=0$。

2. 对字符串A与字符串B进行匹配，求出一个数组f，其中$f[i]$表示B中以i结尾的子串与A的前缀能够匹配的最大长度，即：$f[i]=max\{j\}，其中j\le i并且B[i-j+1:i]=A[1:j]$。

next数组的计算方法：

next[1] = 0，接下来依次求2-N的值；
假设$next[1:i-1]$已经计算完毕，计算$next[i]$时，根据定义，我们需要找出所有满足$j<i且A[i-j+1:i]-A[1:j]$的整数j并取最大值，为了叙述方便，称满足这两个条件的j为$next[i]$的候选项。

引理：
若$j_0$是$next[i]$的一个候选项，则小于$j_0$的最大的$next[i]$的候选项是$next[j_0]$；换言之，$next[j_0]+1:j_0-1$之间的数都不是$j_0$的候选项。

使用优化的算法计算$next$数组：
根据引理，当$next[i-1]$计算完毕时，我们可以知道其所有的候选项从大到小依次为：$next[i-1],next[next[i-1]],\cdots$；同时，如果一个整数j是next[i]的候选项，那么显然j - 1是next[i - 1]的候选项（结合前面的定义思考为什么）；因此，在计算$next[i]$的时候，只需要把$next[i-1]+1,next[next[i-1]]+1,\cdots$作为j的候选项即可。

按照上述思路实现求next和f数组的代码：

next数组的求法：

next[1] = 0;

for (int i = 2, j = 0; i <= n; ++i)
{
    while (j > 0 && a[i] != a[j + 1]) j = next[j];
    if (a[i] == a[j + 1]) ++j;
    next[i] = j;
}

• 初始化next[1] = 0
• 不断尝试扩张匹配长度j，如果扩展失败（下一个字母不相等），令$j=next[j]$，直到变为0（从头开始匹配）
• 如果能够扩展成功，j就增加一
• 经过了上面的操作，$next[i]$的答案就是j

f数组的求法：

for (int i = 1, j = 0; i <= m; ++i)
{
    while (j > 0 && (j == n || b[i] != a[j + 1])) j = next[j];
    if (b[i] == a[j + 1]) ++j;
    f[i] == j;

    if (f[i] == n)
    {
        // do something（表明a在b中出现一次）
    }
}

以上就是KMP算法的实现，时间复杂度$\Theta (N+M)$。

例题：POJ1961 Period

给定一个字符串S，求其每一个前缀是否是由若干个循环节构成，如果是的话，输出此前缀的长度和循环节的个数（如“aabaab”应该输出6 2）。

首先，对字符串S子匹配求出next数组，根据定义，对于每一个i，都有$S[1:next[i]]=S[i-next[i]+1:i]$，且不存在更大的$next[i]$满足这个条件。

引理：
$S[1:i]$存在长度为$len,len<i$的循环节的充要条件是：len能够整除i并且$S[len+1:i]=S[1:i-len]$，即$i-len$是$next[i]$的候选项！

程序如下：

constexpr int MAX = 1000000 + 5;

int next[MAX], n;
char s[MAX];

void getNext()
{
    ::next[1] = 0;
    for (int i = 2, j = 0; i <= n; ++i)
    {
        while (j > 0 && s[i] != s[j + 1]) j = ::next[j];
        if (s[i] == s[j + 1]) ++j;
        ::next[i] = j;
    }
}

int main()
{
    int cases = 1;

    while (cin >> n && n)
    {
        scanf("%s", s + 1);
        getNext();

        printf("Test case #%d\n", cases++);

        for (int i = 2; i <= n; ++i)
        {
            if (i % (i - ::next[i]) == 0 && i / (i - ::next[i]) > 1)
            {
                printf("%d %d\n", i, i / (i - ::next[i]));
            }
        }
        printf("\n");
    }
}

最小表示法

定义：
给定一个字符串$S[1:N]$，如果我们不断将字符串末尾的字符取出来，并放到开头，追终会得到N个字符串，我们称这N个字符串是循环同构的；而这N个字符串中字典序最小的一个，称为原字符串的最小表示。

一个字符串的最小表示可以在$\Theta (N)$的时间内求出，首先，将字符串复制一份到末尾，记为SS，用B[i]表示从S[i]开始的循环同构字符串，很显然，$B[i]=SS[i:i+n-1]$。

现在假设我们在比较$B[i]和B[j]$的字典序，在比较的过程中，发现$SS[i+k]>SS[j+k]$，那么，我们就可以确定，$B[i+1],B[i+2],\cdots ,B[i+k]$的字典序也都比$B[j]$大（不相等的那个位置提前了，字典序越变越大）；
同理，如果$SS[i+k]<SS[j+k]$，则可以跳过$B[j+1],B[j+2],\cdots ,B[j+k]$。

于是，我们可以得出如下程序在$\Theta (N)$的时间内寻找字符串的最小表示：

int n = strlen(s);
for (int i = 1; i <= n; ++i) s[n + i] = s[i];

int i = 1, j = 2, k;
while (n < i && j < n)
{
    for (k = 0; k <= n && s[i + k ] == s[j + k]; ++k);

    if (k == n) break; // 说明原字符串只有一种字符构成，随便哪个都是最小表示

    if (s[i + k] > s[j + k]) 
    {
        i = i + k + 1;
        if (i == j) ++i;
    }
    else 
    {
        j = j + k + 1;
        if (i == j) ++j;
    }
}

int ans = min(i, j); // B[ans]是最小表示

---

Tire

Tire（字典树）是一种用于实现字符串快速检索的多叉树结构。Tire的每个节点都拥有若干个字符指针，若在插入或者检索字符串时扫描到一个字符c，就沿着当前节点c字符的指针，走向该指针指向的节点。

Tire的基本操作

初始化
仅包含根节点，根节点中所有字符指针均为空。

插入
当需要插入字符串S时，我们先令一个指针P指向根节点，然后依次扫描S中的每一个字符c：

• 若P的指向c的指针指向一个已经存在的节点Q，则令P = Q；
• 若P的指向c的指针为空，则新建一个节点Q，令c的指针指向Q，之后令P = Q；

当S中的所有字符均扫描完毕时，在当前节点P上标记其为一个字符串的末尾。

检索
当需要检索一个字符串S在Tire中是否存在时，我们另一个指针P指向根节点，然后依次扫描S中的每一个字符c：

• 如果P的指向c的指针为空，说明S在Tire中不存在，结束检索；
• 如果P的指向c的指针指向一个存在的节点Q，则令P = Q；

当S中的所有字符均扫描完毕是，若当前节点P被标记为一个字符串的末尾，说明S在Tire中存在，否则，S不存在。

空间复杂度为$\Theta (N\times C)$，其中N为节点的个数，C为字符集的大小。

数组字典树模板：

字符集为所有小写字母。

int tire[MAX][26], cnt = 1;
bool isEnd[MAX];

void insert(string s)
{
    int pos = 1; // 根节点

    for (auto c : s)
    {
        int ch = c - 'a';

        if (tire[pos][ch] == 0) tire[pos][ch] = ++cnt; // 如果不存在，插入

        pos = tire[pos][ch]; // 下一个“节点”的位置
    }

    isEnd[pos] = true;
}

bool query(string s)
{
    int pos = 1;

    for (auto c : s)
    {
        pos = tire[pos][c - 'a'];
        if (pos == 0) return false;
    }

    return isEnd[pos];
}

例题：CH1601 前缀统计

先给定一组字符串，然后进行询问，每次询问给出一个字符串，求之前给定的字符串中有多少是其前缀。

constexpr int MAX = 1000000 + 5;

int tire[MAX][26], tail[MAX], cnt = 1, n, m;

void insert(string s)
{
    int pos = 1;

    for (auto c : s)
    {
        int val = c - 'a';

        if (tire[pos][val] == 0) tire[pos][val] = ++cnt;

        pos = tire[pos][val];
    }

    tail[pos]++;
}

int query(string s)
{
    int pos = 1, ans = 0;

    for (auto c : s)
    {
        int val = c - 'a';

        pos = tire[pos][val];

        if (pos == 0) return ans;

        ans += tail[pos];
    }

    return ans;
}

int main()
{
    cin >> n >> m;

    string s;
    while (n--)
    {
        cin >> s;
        insert(s);
    }

    while (m--)
    {
        cin >> s;
        cout << query(s) << endl;
    }
}

例题：CH1602 The XOR Largest Pair

给定$N$个整数：$A-1,A_2,\cdots ,A_N$，任选两个进行异或运算，最大值是多少？

把每一个整数看作32位的01字符串，每读入一个整数，就先在字典树中寻找可能的最优解（每一位都尽量取反），更新答案，再把这个数插入进字典树。

constexpr int MAX = 100000 + 5;

int tire[MAX * 32 + 5][2], cnt = 1, tmp, n, ans;

void insert(int val)
{
    int pos = 1;

    for (int k = 30; k >= 0; --k)
    {
        int ch = val >> k & 1;

        if (tire[pos][ch] == 0) tire[pos][ch] = ++cnt;

        pos = tire[pos][ch];
    }
}

int query(int val)
{
    int ret = 0, pos = 1;

    for (int k = 30; k >= 0; --k)
    {
        int ch = val >> k & 1;

        if (tire[pos][ch ^ 1])
        {
            pos = tire[pos][ch ^ 1];
            ret |= 1 << k; // think here
        }
        else
        {
            pos = tire[pos][ch];
            // 只要有一个数已经插入，就不会有找不到下一个节点的情况
        }
    }

    return ret;
}

int main()
{
    cin >> n;

    while (n--)
    {
        cin >> tmp;
        insert(tmp);

        ans = max(ans, query(tmp)); // think here
    }

    cout << ans << endl; // and here
}

例题：POJ3764 The XOR Longest Path

给一棵树，树上的每一条边都有一个权值，从树上选择两个点，将这两个点之间所有的边之间的权值异或起来，能得到的最大的结果是多少？

首先，进行一遍DFS算出所有节点到根节点的所有边权的异或值，然后，对这些值进行上一题的操作。

书本标程：

const int u = 100010;
int ver[2 * u], edge[2 * u], next[2 * u], \
	head[u], v[u], val[u * 32], a[u * 32][2], f[u];

int n, tot, i, ans, x, y, z;

void add(int x, int y, int z)
{
	ver[++tot] = y;
	edge[tot] = z;
	next[tot] = head[x];
	head[x] = tot;
}

void dfs(int x)
{
	v[x] = 1;
	for (int i = head[x]; i; i = next[i])
		if (!v[ver[i]])
		{
			f[ver[i]] = f[x] ^ edge[i];
			dfs(ver[i]);
		}
}

void ins(int x, int y, int temp)
{
	if (y < 0)
	{
		val[x] = temp;
		return;
	}
	int z = (temp >> y) & 1;
	if (!a[x][z])
		a[x][z] = ++tot;
	ins(a[x][z], y - 1, temp);
}

int get(int x, int y, int temp)
{
	if (y < 0)
		return val[x];
	int z = (temp >> y) & 1;
	if (a[x][z ^ 1])
		return get(a[x][z ^ 1], y - 1, temp);
	else
		return get(a[x][z], y - 1, temp);
}

int main()
{
	while (cin >> n)
	{
		memset(head, 0, sizeof(head));
		memset(f, 0, sizeof(f));
		memset(v, 0, sizeof(v));
		tot = 0;
		for (i = 1; i < n; i++)
		{
			scanf("%d%d%d", &x, &y, &z);
			x++, y++;
			add(x, y, z);
			add(y, x, z);
		}
		dfs(1);
		tot = 1;
		ans = 0;
		memset(a, 0, sizeof(a));
		ins(1, 30, 0);
		for (i = 1; i <= n; i++)
		{
			ans = max(ans, f[i] ^ get(1, 30, f[i]));
			ins(1, 30, f[i]);
		}
		cout << ans << endl;
	}
	return 0;
}

---

二叉堆

二叉堆是一种支持插入、删除、查询最值的数据结构，是一棵满足堆性质的完全二叉树，树上的每一个节点都带有一个权值。

大根堆：
树上任意一个节点的权值都小于等于其父节点的权值。

小根堆：
树上任意一个节点的权值都大于等于其父节点的权值。

二叉堆的储存可以采用层次序列的储存方式，直接用一个数组保存：按从左到右，从上到下的顺序依次为二叉堆上的节点编号，如果根节点的编号为1的话，每个节点的左子节点的编号为根节点编号 * 2，右子节点的编号为根结点编号* 2 + 1，每个节点的根节点的编号为自身编号 / 2。

以大根堆为例讨论二叉堆的常见操作：

二叉堆的插入操作：

将新插入的值放在储存二叉堆的数组的末尾，然后按照二叉堆的规则向上交换，直到满足二叉堆的性质，时间复杂度为二叉堆的深度，即：$\Theta (logN)$。

返回堆顶值：
大根堆堆顶的值为堆中的最大值，小根堆堆顶的值为堆中的最小值。

移除堆顶的值：
首先，将堆顶的值与数组末尾的节点交换，之后移除数组末尾的节点（在下面的样例中，移除节点通过记录节点个数的n-1来实现）；然后，将新的堆顶的值通过交换的方式向下调整，直至满足二叉堆的性质。

删除任意一个元素：
与删除对顶元素类似，将要删除的元素与数组末尾的元素交换，时候数组长度-1，然后分别检查是否需要向上或者向下调整，时间复杂度为$\Theta (logN)$。

示例代码：

int heap[MAX], n;

void up(int pos) // 向上调整
{
    while (pos > 1)
    {
        if (heap[pos] > heap[pos / 2])
        {
            swap(heap[pos], heap[pos / 2]);
            pos /= 2;
        }
        else
            break;
    }
}

void insert(int val) // 插入节点
{
    heap[++n] = val;
    up(n);
}

int top() // 返回堆顶元素
{
    return heap[1];
}

void down(int pos) // 向下调整
{
    int son = pos * 2;
    while (son <= n)
    {
        if (son < n && heap[son] <= heap[son + 1])
            son++; // 最大的子节点

        if (heap[pos] < heap[son])
        {
            swap(heap[pos], heap[son]);
            pos = son;
            son = pos * 2;
        }
        else
            break;
    }
}

void pop() // 弹出堆顶元素
{
    heap[1] = heap[n];
    n--;
    down(1);
}

void remove(int pos) // 删除指定位置的元素
{
    heap[pos] = heap[n];
    n--;
    up(pos);
    down(pos);
}

C++STL中的priority_queue默认为一个大根堆。

例题：POJ1456 Supermarket

给定N个商品，每个商品都有一个利润$p_i$属性和一个过期时间$d_i$属性，每天只能卖出一个商品，求如何安排每天的商品，使得利润最大。

贪心策略：对于每一个天数t，尽量卖出利润前t大的商品。

首先，将所有商品按照过期时间排序；
然后，建立一个空的小根堆，节点权值为利润；

接下来，扫描每一个商品：

• 如果当前扫描到的商品的过期时间t等于堆中的商品个数，说明在当前方案下，前t天已经安排了t个商品；此时，若当前扫描到的商品的利润大于堆顶商品的利润，则替换堆顶的元素。

• 如果当前扫描到的商品的过期时间大于堆中的商品的个数，直接插入。

扫描完成后，堆中的商品就是最优解。

总时间复杂度：$\Theta (NlogN)$。

constexpr int MAX = 10000 + 5;

struct good
{
    int val, day;

    friend bool operator<(good a, good b)
    {
        return a.val > b.val;
    }
}
goods[MAX];

bool cmp(good a, good b)
{
    return a.day < b.day;
}

int n;

int main()
{
    while (cin >> n)
    {
        for (int i = 0; i < n; ++i)
        {
            cin >> goods[i].val >> goods[i].day;
        }

        sort(goods, goods + n, cmp);

        priority_queue <good> ans;

        for (int i = 0; i < n; ++i)
        {
            if (goods[i].day > ans.size())
                ans.push(goods[i]);
            else if (goods[i].day == ans.size())
            {
                if (ans.top().val < goods[i].val)
                {
                    ans.pop();
                    ans.push(goods[i]);
                }
            }
        }

        int fuck = 0;
        while (!ans.empty())
        {
            fuck += ans.top().val;
            ans.pop();
        }

        cout << fuck << endl;
    }
}

例题：POJ2442 Sequence

给定M个长度为N的序列，从每一个序列中选择一个数然后求和，可以得到$N^M$个和，求其中最小的N个和。

先考虑当$M=2$时的简化的问题，设这两个序列为A和B，分别升序排序。

很显然，最小和是$A[1]+B[1]$，次小和是$min(A[1]+B[2],A[2]+B[1])$。

假设次小和是$A[2]+B[1]$，则第三小和为$A[1]+B[2],A[2]+B[2],A[3]+B[1]$三者之一，也就是说，当$A[i]+B[j]$确定为第k小之后，$A[i+1]+B[j],A[i]+B[j+1]$就会加入第K + 1小的备选答案集合。

选要注意的是，$A[i]+B[j+1]$与$A[i+1]+B[j]$都可以产生$A[i+1]+B[j+1]$这个备选答案，为了避免重复我们可以规定如果上一个答案是增加j产生的，那么之后也只能增加j。

我们可以建立一个小根堆，节点储存三元组$(i,j,last)$，last表示上一次是否移动了j，以$A[i]+B[j]$作为节点的权值。

• 起初，堆中只有$(1,1,false)$
• 取出堆顶$(i,j,last)$，然后将$(i,j+1,true)$插入堆，如果$last=false$，就再插入$(i+1,j,false)$
• 循环N次之后，每一次取出的堆顶值构成前N个最小值，时间复杂度$\Theta (NlogN)$。

对于本题，可以先求前两个序列的前N小，再把结果和第三个序列一起求前N小，以此类推，得出最终答案，总时间复杂度$\Theta (MNlogN)$。

int n, m, mat[105][2005], tmp[2005];

struct node
{
    int i, j, val_i, val_j;
    bool last;

    node(int i, int j, int val_i, int val_j, bool last)
    {
        this->i = i;
        this->j = j;
        this->val_i = val_i;
        this->val_j = val_j;
        this->last = last;
    }

    friend bool operator<(node a, node b)
    {
        return (a.val_i + a.val_j) > (b.val_i + b.val_j);
    }
};

void merge(int index)
{
    int a = index - 1;
    int b = index;

    priority_queue <node> q;

    q.push(node(0, 0, mat[a][0], mat[b][0], false));

    int cnt = 0;
    while (!q.empty())
    {
        node now = q.top();
        q.pop();

        tmp[cnt++] = now.val_i + now.val_j;

        if (now.j + 1 < m)
            q.push(node(now.i, now.j + 1, mat[a][now.i], mat[b][now.j + 1], true));

        if (!now.last && now.i + 1 < m)
            q.push(node(now.i + 1, now.j, mat[a][now.i + 1], mat[b][now.j], false));

        if (cnt == m) break;
    }

    for (int i = 0; i < m; ++i)
    {
        mat[index][i] = tmp[i];
    }
}

int main()
{
    int cases;
    cin >> cases;

    while (cases--)
    {
        cin >> n >> m;
        for (int i = 0; i < n; ++i)
        {
            for (int j = 0; j < m; ++j)
            {
                cin >> mat[i][j];
            }

            sort(mat[i], mat[i] +m);
        }

        for (int i = 1; i < n; ++i)
            merge(i);

        for (int i = 0; i < m; ++i)
        {
            if (i) cout << ' ';
            cout << mat[n - 1][i];
        }
        cout << endl;
    }
}

例题：BZOJ数据备份

中文题面，略。

最优解中每两个配对的办公楼一定是相邻的，于是，首先，处理出每两个相邻的办公楼之间的距离$D_1,D_2,\cdots ,D_{N-1}$；此时问题转化为：从D中选择K个数，相邻的两个数不能同时选，使他们的和最小。

如果$K=1$，答案显然是D中的最小值；
如果$K=2$，设$D_i$为D中的最小值，则最优解为以下两种情况之一：

• 选择$D_i$以及除$D_{i-1},D_{i+1}$之外的最小值。
• 选择$D_{i-1}$和$D_{i+1}$。

所以，我们可以发现：最小值左右两侧的值要么同时选，要么都不选。

所以，对于先择K个数的问题，我们可以选择D中的最小值$D_i$，然后将$D_{i-1},D_i,D_{i+1}$从数列中删除，再将$D_{i+1}+D_{i-1}-D_i$插入刚刚执行删除的位置，最后，问题转化为从剩下的数中选择K - 1个数，和最小。

在转化后的子问题中，如果选择了$D_{i-1}+D_{i+1}-D_i$，相当于选择了$D_{i-1}+D_{i+1}$，涵盖了上面的两种情况。

综上所述，解题方法如下：
建立一个有$N-1$个节点的链表，储存相邻建筑的距离，节点上的值分别为$D_1,D_2,\cdots ,D_{N-1}$，然后建立一个小根堆，与链表构成映射关系，也就是说堆中也有N - 1个节点，权值分别为$D_1,D_2,\cdots ,D_{N-1}$，然后记录下组成映射关系的指针。

每次弹出堆顶的值，累加到答案中，然后按照上面给出的操作，在链表中删除$D_i,D_{i-1},D_{i+1}$并将$D_{i+1}+D_{i-1}-D_i$插入链表并调整小根堆。

详情见代码。

光盘自带的代码我用了好久才看明白，真正的dalao的思维能力真的可怕。

自己手动copy的代码：
简单做了一点注释

int arr[100000 + 5], // 储存原始的坐标数据，之后处理出相邻楼的距离，作为数组链表
    pre[100000 + 5], // 记录“链表”某一项的前驱
    nex[100000 + 5], // 记录“链表”某一项的后继
    tree[100000 + 5], // arr数组下标到ptr数组下标之间的映射
    ptr[100000 + 5],  // 小根堆数组，记录arr数组的下标
    n, k, ans, cnt;

void up(int pos)
{
    while (pos > 1)
    {
        if (arr[ptr[pos]] < arr[ptr[pos / 2]]) // ptr数组是小根堆，由于储存的是arr数组的下标，故如此比较
        {
            swap(ptr[pos], ptr[pos / 2]); // ptr和tree数组要一起交换
            swap(tree[ptr[pos]], tree[ptr[pos / 2]]);
            pos /= 2;
        }
        else
            break;
    }
}

void down(int pos)
{
    int son = pos * 2;
    while (son <= cnt)
    {
        if (son + 1 <= cnt && arr[ptr[son]] > arr[ptr[son + 1]])
            son++; // 调整小根堆的正常操作，搞懂每个数组的意义即可

        if (arr[ptr[pos]] > arr[ptr[son]])
        {
            swap(ptr[pos], ptr[son]);
            swap(tree[ptr[pos]], tree[ptr[son]]);

            pos = son;
            son = pos * 2;
        }
        else
            break;
    }
}

void insert(int x)
{
    ptr[++cnt] = x; // 插入小根堆
    tree[x] = cnt; // 记录映射关系
    up(cnt); // 由于是在末尾插入，向上调整
}

void remove(int x)
{
    ptr[tree[x]] = ptr[cnt]; // 要删除的元素与末尾元素“交换”
    tree[ptr[cnt]] = tree[x]; // 映射关系同时改变
    cnt--; // 堆的大小（数组长度）-1
    up(tree[x]); // 调整
    down(tree[x]);
}

int main()
{
    cin >> n >> k;

    for (int i = 1; i <= n; ++i)
        cin >> arr[i];

    for (int i = 1; i < n; ++i)
    {
        arr[i] = arr[i + 1] - arr[i];
        nex[i] = i + 1;
        pre[i + 1] = i;
        insert(i); // 这里的初始化相信都能看懂
    }

    for (int i = 1; i <= k; ++i) // 具体操作
    {
        int now = ptr[1];
        ans += arr[now];

        if (pre[now] == 0 && nex[now] == n)
            break;

        if (pre[now] == 0)
        {
            remove(now);
            remove(nex[now]);
            pre[nex[nex[now]]] = 0;
        }
        else if (nex[now] == n)
        {
            remove(now);
            remove(pre[now]);
            nex[pre[pre[now]]] = n;
        }
        else
        {
            remove(now);
            remove(nex[now]);
            remove(pre[now]);

            arr[now] = arr[pre[now]] + arr[nex[now]] - arr[now];

            insert(now);

            pre[now] = pre[pre[now]];
            nex[pre[now]] = now;
            nex[now] = nex[nex[now]];
            pre[nex[now]] = now;
        }
    }

    cout << ans << endl;
}

书本自带的标程：

int f[100010], a[100010], pre[100010], next[100010], v[100010];
int n, m, p, i, x, ans;

void up(int p)
{
	while (p > 1)
		if (a[f[p]] < a[f[p >> 1]])
		{
			swap(f[p], f[p >> 1]);
			swap(v[f[p]], v[f[p >> 1]]);
			p >>= 1;
		}
		else
			break;
}

void down(int l, int r)
{
	int t = 2 * l;
	while (t <= r)
	{
		if (t < r && a[f[t]] > a[f[t + 1]])
			t++;
		if (a[f[l]] > a[f[t]])
		{
			swap(f[l], f[t]);
			swap(v[f[l]], v[f[t]]);
			l = t, t = 2 * l;
		}
		else
			break;
	}
}

void insert(int x)
{
	f[++p] = x;
	v[x] = p;
	up(p);
}

void erase(int x)
{
	f[v[x]] = f[p];
	v[f[p]] = v[x];
	p--;
	up(v[x]), down(v[x], p);
}

int main()
{
	cin >> n >> m;

	for (i = 1; i <= n; i++)
		scanf("%d", &a[i]);

	for (i = 1; i < n; i++)
	{
		a[i] = a[i + 1] - a[i];
		next[i] = i + 1, pre[i + 1] = i;
		insert(i);
	}
	for (i = 1; i <= m; i++)
	{
		x = f[1];

		ans += a[x];

		if (pre[x] == 0 && next[x] == n)
			break;

		if (pre[x] == 0)
		{
			erase(x), erase(next[x]);
			pre[next[next[x]]] = 0;
		}

		else if (next[x] == n)
		{
			erase(x), erase(pre[x]);
			next[pre[pre[x]]] = n;
		}

		else
		{
			erase(x), erase(pre[x]), erase(next[x]);
			a[x] = a[pre[x]] + a[next[x]] - a[x];
			insert(x);
			pre[x] = pre[pre[x]];
			next[pre[x]] = x;
			next[x] = next[next[x]];
			pre[next[x]] = x;
		}

	}

	cout << ans << endl;
	
	return 0;
}

Huffman树

考虑这样一个问题：构造一棵包含$n$个叶子节点的$k$叉树，其中第$i$个叶子节点的权值为$w_i$，求最小的$\sum w_i\times l_i$，其中$l_i$为第$i$个叶子节点到根节点的距离；这样的问题的解被称为k叉Huffman树。

为了最小化$\sum w_i\times l_i$，权值较大的叶子节点的深度应该尽可能的小，当$k=2$时，使用贪心算法求解过程如下：

1. 建立一个小根堆，插入这$n$个叶子节点的权值。
2. 取出堆中最小的两个权值：$w_1,w_2$，并令$ans+=w_1+w_2$。
3. 建立一个权值为$w_1+w_2$的树节点p，令p成为$w_1$和$w_2$两个叶子节点的父节点。
4. 在小根堆中插入$w_1+w_2$。
5. 重复步骤2-4，直到小根堆的大小为1。

最后，所有新建的p与原来的叶子节点构成的树就是Huffman树，ans的值就是$\sum w_i\times l_i$的最小值。

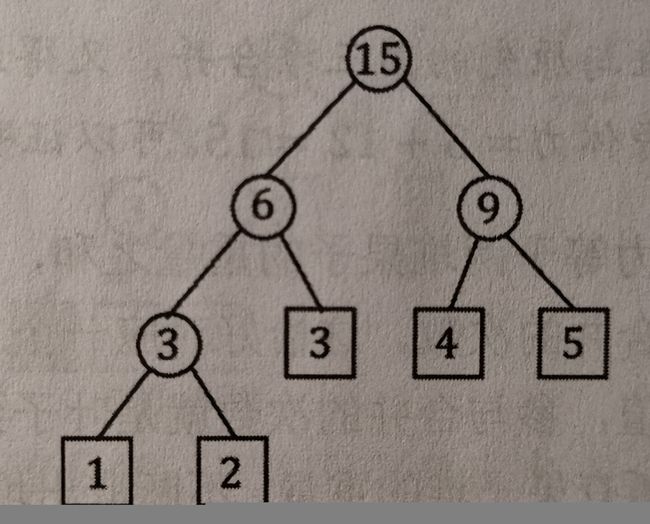
如图所示为对叶子节点1，2，3，4，5按照上述过程建立Huffman树的结果。

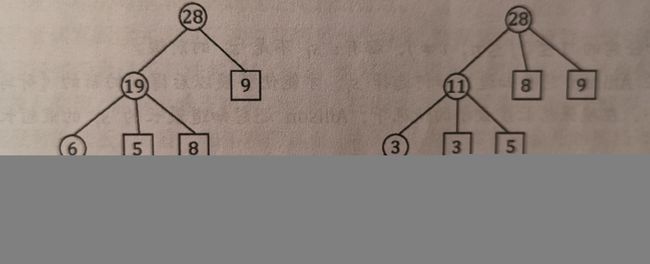
对于$k>2$的Huffman树，除了应该用上述算法之外，还要考虑在最后一轮中能够取出的节点不足$k$个的情况，对于这种情况，最简单的方法是额外插入一些权值为0的叶子节点使得叶子节点的个数满足$(n-1)mod(k-1)=0$，如图：

例题：CH1701 合并果子

有N堆果子，已知每一堆果子的重量，下载要把他们合并成一对，每一次合并，可以合并任意两堆果子，消耗的体力等于两堆果子的重量和，经过N-1次合并，所有果子都会被合并成一堆，求这过程中消的体力的最小值。

最简单的一颗二叉Huffman树。

int main()
{
    int n, ans = 0, w;
    priority_queue <int, vector <int>, greater <int> > q;

    cin >> n;
    while (n--)
    {
        cin >> w;
        q.push(w);
    }

    while (q.size() > 1)
    {
        int w1 = q.top(); q.pop();
        int w2 = q.top(); q.pop();

        q.push(w1 + w2);

        ans += w1 + w2;
    }

    cout << ans << endl;
}

例题：荷马史诗

Huffman树用于文本压缩。

将单词出现的次数$w_1,w_2,\cdots ,w_n$作为Huffman树叶子节点的权值，然后求k叉Huffman树，对于每一个节点的k个分支，分别在分支上标记1~k-1。

本题还要求处理后的最长字符串的最小长度，我们只需要在求解HUffman树的时候，对于权值相同的节点，优先考虑当前深度小的节点即可。

代码：

typedef long long ll;

struct node
{
    ll weight, height;

    node(ll w = 0, ll h = 0)
    {
        this->height = h;
        this->weight = w;
    }

    friend bool operator<(node a, node b)
    {
        return a.weight > b.weight || \
        (a.weight == b.weight && a.height > b.height);
        // 优先比较权值，权值相等深度小的优先
    }
};

int main()
{
    ll n, k, ans = 0;
    priority_queue <node> q;

    cin.sync_with_stdio(false);
    cin.tie(0);

    cin >> n >> k;

    for (int i = 0; i < n; ++i)
    {
        ll w;
        cin >> w;
        q.push(node(w, 0));
    }

    while ((q.size() - 1) % ( k -1) != 0)
        q.push(node(0, 0));

    while (q.size() >= k)
    {
        ll w = 0, m = -1;

        for (int i = 0; i < k; ++i)
        {
            w += q.top().weight; // 取出k个节点组成新结点并累计答案
            m = max(m, q.top().height);
            q.pop();
        }

        q.push(node(w, m + 1)); // 新的节点的深度是k个节点中的最大深度+1
        ans += w;
    }

    cout << ans << endl;
    cout << q.top().height << endl; // 不会出现权值最小的深度不是最大的情况
}

---

总结与练习

习题估计到退役都不一定会碰。