LIS 最长上升子序列问题（动态规划、贪心+二分）

参考一篇大佬博客学习到的解题方法：LIS（最长上升子序列）问题的三种求解方法以及一些例题

最长上升子序列

首先要理解两个概念：

1. 子串

串中任意个连续的字符组成的子序列称为该串的子串

对于一个字符串变量，例如"abcde",它的子串就是像"abc"这样可以从中找到的连续的字符串。字符串"abcde"本身也属于它本身最长的子串。

子串个数计算：
abc 的子串：a、 b、 c、 ab、 bc 、abc、/0共（3+2+1+1）个，
若字符串的长度为 n,则子串的个数就是[n*(n+1)/2+1]个, 例如："software"中子串的个数就是8+7+…+1+1=37个，即为37个。
特别的！对于有连续相同的子串(例如:AAABBBCCC)这样的子串的计算方法是n(n+1)/2+1-重复子串
 

2. 子序列

子序列就是在原来序列中找出一部分组成的序列, 不一定连续但先后顺序与原序列一致

如 “abcdefg” 中，acd，bdf 属于它的子序列，而 bac，dbfg 则不是，因为它们与字符串的字符顺序不一致。
 
区别：
最长公共子序列（LCS） 是一个在一个序列集合中（通常为两个序列）用来查找所有序列中最长子序列的问题。这与查找最长公共子串的问题不同的地方是：子序列不需要在原序列中占用连续的位置； 而最长公共子序列必须连续。
 
 

LIC定义

最长上升子序列（Longest Increasing Subsequence），简称LIS，是一个在一个序列集合中（通常为两个序列）用来查找所有序列中最长子序列的问题。也有些情况求的是最长非降序子序列，二者区别就是序列中是否可以有相等的数。
假设我们有一个序列 b i，当b1 < b2 < … < bn 的时候，我们称这个序列是上升的。对于给定的一个序列(a1, a2, …, aN)，我们也可以从中得到一些上升的子序列(ai1, ai2, …, aiK)，这里1 <= i1 < i2 < … < iK <= N，但必须按照从前到后的顺序。比如，对于序列(1, 7, 3, 5, 9, 4, 8)，我们就会得到一些上升的子序列，如(1, 7, 9), (3, 4, 8), (1, 3, 5, 8)等等，而这些子序列中最长的（如子序列(1, 3, 5, 8) ），它的长度为4，因此该序列的最长上升子序列长度为4。

如果光看定义的话会发现比较难理解，所以先看个例题

例题：广场舞队伍

题目链接：
来源：牛客网
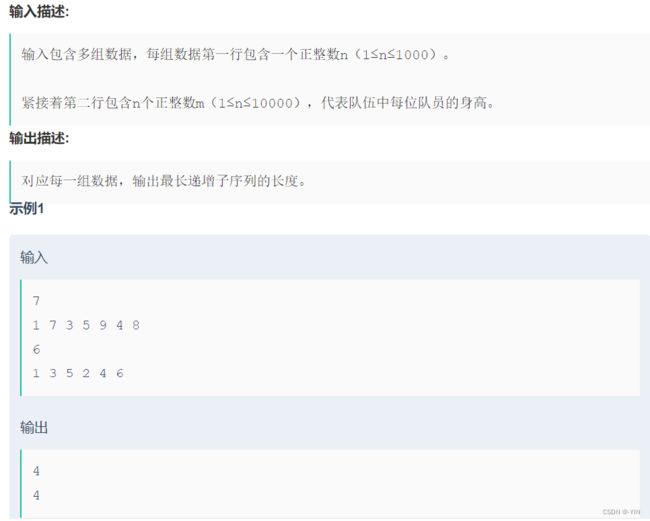
广场上站着一支队伍，她们是来自全国各地的扭秧歌代表队，现在有她们的身高数据，请你帮忙找出身高依次递增的子序列。 例如队伍的身高数据是（1、7、3、5、9、4、8），其中依次递增的子序列有（1、7），（1、3、5、9），（1、3、4、8）等，其中最长的长度为4。

分析：对于固定的数组，虽然LIS序列不一定唯一，但LIS的长度是唯一的。
从题目给出的例子来看

动态规划

时间复杂度 O(n²), 空间复杂度 O(n)

给出与序列长度大小相等的 dp 数组，下标 i 表示 以 arr[ i ] 结尾的 LIS 的长度

状态转移方程：dp[i] = max( dp[i]，dp[j] + 1)

d(i) 就是找以A[ i ]结尾的最长子序列，在 A[ i ] 之前的最长上升子序列+1，即前 i 个数的 LIS 长度 + 1。当 A[ i ] 之前没有比 A[ i ] 更小的数时，d(i) = 1。所有的d(i)里面最大的那个就是最长上升子序列。
其实说的通俗点，就是每次都向前找比它小的数与比它大的数的位置，将第一个比它大的替换掉，这样操作虽然LIS序列的具体数字可能会变，但是很明显LIS长度还是不变的

#include 
#include 
using namespace std;

// 动态规划
size_t MostAddSub(vector<int>& v){
    vector<int> dp(v.size(), 1);
    size_t sum = 1;
    for(size_t i = 0; i < v.size(); ++i){
        for(size_t j = 0; j < i; ++j){
            if(v[i] > v[j])
                dp[i] = dp[i] > dp[j]+1 ? dp[i] : dp[j]+1;
        }
        sum = sum > dp[i] ? sum : dp[i];
    }
    return sum;
}

int main()
{
	int n;
	while (cin >> n){
		vector<int> v(n);
		for (int i = 0; i < n; ++i)
			cin >> v[i];
        cout << MostAddSub(v) << endl;
    }
	return 0;
}

 
 

贪心+二分法

时间复杂度 O(nlogn), 空间复杂度 O(n)

大佬文章中的解释

新给一个 low 数组，low [ i ]表示长度为 i 的LIS结尾元素的最小值。对于一个上升子序列，显然其结尾元素越小，越有利于在后面接其他的元素，也就越可能变得更长。因此，我们只需要维护 low 数组，对于每一个a[ i ]，如果a[ i ] > low [当前最长的LIS长度]，就把 a [ i ]接到当前最长的LIS后面，即low [++当前最长的LIS长度] = a [ i ]。
 
对于每一个a [ i ]，如果a [ i ]能接到 LIS 后面，就接上去；否则，就用 a [ i ] 取更新 low 数组。具体方法是，在low数组中二分查找找到第一个大于等于a [ i ]的元素low [ j ]，用a [ i ]去更新 low [ j ]。如果从头到尾扫一遍 low 数组的话，时间复杂度仍是O(n^2)。我们注意到 low 数组内部一定是单调不降的，所有我们可以二分 low 数组，找出第一个大于等于a[ i ]的元素。二分一次 low 数组的时间复杂度的O(lgn)，所以总的时间复杂度是O(nlogn)。

不得不说，有二分的地方二分的边界永远是最恶心的最难搞的，整体思路不难。

1. 新建一个长度为 n+1 的数组 low ，数组 low[i]表示长度为 i 的最长上升子序列的末尾元素的最小值。

即数组 1,2,3,4,5,6中长度为3的上升子序列可以为 1,2,3也可以为 2,3,4等等，但是d[3]=3，即子序列末尾元素最小为3（1,2,3）

2. low 数组具有单调性，即表明：（1）可以使用二分法；（2）数组 low 的长度即为最长子序列的长度；

我们接着需要证明数组 low 具有单调性，即证明 ilow [j]，但在长度为j，末尾元素为low [j]的子序列A中，将后 j-i 个元素减掉，可以得到一个长度为 i 的子序列B，其末尾元素 t1 必然小于low [j]（因为在子序列A中，t1的位置上在d[j]的后面），而我们假设数组 low 必须符合表示长度为 i 的最长上升子序列的末尾元素的最小值，此时长度为i的子序列的末尾元素t1 < low [j] < low [k]，即t1

// 二分查找v中第一个>=num的元素下标
size_t Binary_search(vector<int>& low, int right, int num){
	int left = 1, mid;
	while (left <= right){
		mid = ((right-left)>>1)+left;
		if (low[mid] < num)
            left = mid + 1;
		else
			right = mid - 1;
	}
	return left;
}
// 计算最大升序子序列长度
size_t FIS(vector<int>& v){
    vector<int> low(v.size()+1, 0);
    size_t retLen = 1;
    low[retLen] = v[0];
    for(size_t i = 1; i < v.size(); ++i){
        if(low[retLen] < v[i])
            low[++retLen] = v[i];
        else
            low[Binary_search(low, retLen, v[i])] = v[i];//二分查找
    }
    return retLen;
}

利用二分查找接口：
或着可以使用 STL库中 中提供的二分查找值位置(lower_bound())的方法

STL中关于二分查找的函数有三个lower_bound 、upper_bound 、binary_search 。这三个函数都运用于有序区间（当然这也是运用二分查找的前提）。
其中如果寻找的 val 存在，那么lower_bound返回一个迭代器指向其中第一个这个元素。upper_bound返回一个迭代器指向其中最后一个这个元素的下一个位置（明确点说就是返回在不破坏顺序的情况下，可插入value的最后一个位置）。如果寻找的value不存在，那么lower_bound和upper_bound都返回“假设这样的元素存在时应该出现的位置”。
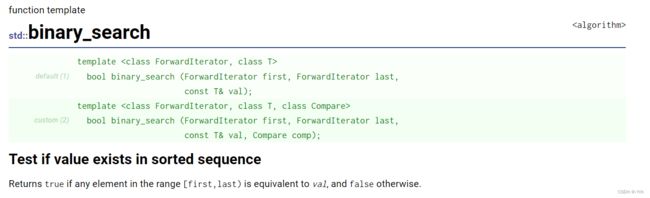
binary_search试图在已排序的[first,last)中寻找元素val，若存在就返回true，若不存在则返回false。返回单纯的布尔值也许不能满足需求，而lower_bound、upper_bound能提供额外的信息。事实上由源码可知binary_search便是利用lower_bound求出元素应该出现的位置，然后再比较该位置 的值与value的值。该函数有两个版本一个是operator< ，另外一个是利用仿函数comp进行比较。

binary_search 这个方法是判断val是否在序列中，返回的是bool值，这个题没法使用

详见：STL二分查找——lower_bound 、upper_bound 、binary_search

    int lengthOfLIS(vector<int>& nums) {
        vector<int> low;
        low.push_back(nums[0]);
        for(int i = 1; i < nums.size(); ++i){
            if(low.back() < nums[i])
                low.push_back(nums[i]);
            else{
                // lower_bound 返回找到位置的迭代器
                *(lower_bound(low.begin(), low.end(), nums[i]))=nums[i];
            }
        }
        return low.size();
    }