算法学习笔记 4-1 二分算法(Binary-Search):致敬经典,超越经典 与 LeetCode真题(Java)
喜欢该类型文章可以给博主点个关注,博主会持续输出此类型的文章,知识点很全面,再加上LeetCode的真题练习,每一个LeetCode题解我都写了详细注释,比较适合新手入门数据结构与算法,后续也会更新进阶的文章。
课件参考—开课吧《门徒计划》
4-1 二分算法(Binary-Search):致敬经典,超越经典
二分算法基础知识
使用二分算法需要有一个基础:必须在有序的数据集合中,才可以使用二分算法。
我们常说的二分算法是一个大类,只要每次操作能把数据规模缩小到原来的一半,我们都管它叫做二分算法,它是一种思维方式。
二分查找
二分查找是二分算法的一个子类,是二分思想的一个具体的算法。
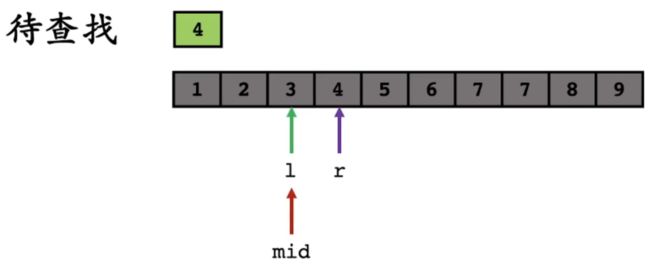
假设我们要找的数字为 4 4 4:
因为 a r r [ m i d ] > 4 arr[mid] > 4 arr[mid]>4,所以更新 r r r 的位置, r = m i d − 1 r=mid-1 r=mid−1:
更新 m i d mid mid 的值:
因为 a r r [ m i d ] < 4 arr[mid] < 4 arr[mid]<4,所以更新 l l l 的位置, l = m i d + 1 l=mid+1 l=mid+1:
再次更新 m i d mid mid:
此时虽然 l l l 和 m i d mid mid 指向同一个位置,但 a r r [ m i d ] < 4 arr[mid] < 4 arr[mid]<4,所以此时 l = m i d + 1 l=mid+1 l=mid+1, l = = r l == r l==r,找到答案:
二分简单代码实现
public class BinarySearch {
public static void main(String[] args) {
int idx = binarySearch(new int[]{1, 2, 3, 4, 5, 6}, 5);
System.out.println(idx); // sout: 4
}
private static int binarySearch(int[] nums, int target) {
int l = 0, r = nums.length - 1, mid;
while (l <= r) {
mid = (l + r) / 2;
if (nums[mid] == target) {
return mid;
} else if (nums[mid] > target) {
r = mid - 1;
} else {
l = mid + 1;
}
}
return -1;
}
}
二分查找—泛型情况
二分的两种变形
- 第一种:假如我们的 t a r g e t = 1 target=1 target=1,我们需要找到最后一个小于等于 1 1 1 的值,和第一个大于等于 1 1 1 的值。
- 第二种:找到第一个出现的 1 1 1,和连续的最后一个出现的 1 1 1。
我们并不能找到 1 1 1 就算结束,需要满足题意的条件。
我们可以把这四种情况总结成一种情况:就是找第一个大于等于给定元素的写法,其它的泛型情况都可以用这一种写法推出来,只需要注意一下下标位置即可。
public class BinarySearch {
public static void main(String[] args) {
int idx = binarySearch2(new int[]{0, 0, 0, 2, 2, 2}, 1);
System.out.println(idx); // sout: 3
}
// 查找第一个大于等于给定值的元素位置
private static int binarySearch2(int[] nums, int target) {
int l = 0, r = nums.length - 1, mid;
while (l <= r) {
mid = (l + r) / 2;
if (nums[mid] == target) {
r = mid - 1; // r指向的值永远不可能是target
} else if (nums[mid] > target) {
r = mid - 1;
} else {
l = mid + 1; // 如果找不到,l指向的值就是数组里面第一个大于等于target的值
}
}
if (l == nums.length) return -1; // 防止越界
return l;
}
}
类似题:LeetCode34. 在排序数组中查找元素的第一个和最后一个位置,在下面会写题解。
时间复杂度
每次二分后,数据都会减少一半: n , n 2 , n 4 , n 8 n,\ \frac{n}{2},\ \frac{n}{4},\ \frac{n}{8} n, 2n, 4n, 8n,所以通项公式为: n 2 k = 1 \frac{n}{2^k}=1 2kn=1
故: k = log 2 n k = \log_2n k=log2n
时间复杂度 O ( log n ) O(\log n) O(logn)
在面试中,如果面试官说,让你用 log n \log n logn 的算法改进一下这个题,只要说到 log n \log n logn 了,一定会用到二分思想(不是二分算法)。
二分中的数组和函数的关系
数组: a r r [ n ] = { 1 , 2 , 3 , 4 , 5 } arr[n] = \{1,2,3,4,5\} arr[n]={1,2,3,4,5}
函数: f x ( a ) = { 1 , 2 , 3 , 4.5 } fx(a)=\{1,2,3,4.5\} fx(a)={1,2,3,4.5},函数根据每次传递的参数不同,将每次的返回时展开后,也可以表示成类似数组的形式。
数组可以二分,那么函数也可以二分。
只要能把问题抽象成一个数学公式(模型)且具有单调性,就能在这个问题上做二分。
三次方根函数图像大概如下图:
函数是有单调性的,有单调性一定可以二分,能二分不一定有单调性。
相关力扣题:LeetCode69. x 的平方根 ,在下面也会写题解。
LeetCode真题
经典面试题—简单二分应用
LeetCode35. 搜索插入位置
难度:easy
请必须使用时间复杂度为
O(log n)的算法。
只要出现这句话,那么就需要使用二分查找去解决。
非常简单的二分,但我们之前写的:如果找不到这个元素会返回 − 1 -1 −1,但是本题要返回它将会被按顺序插入的位置,只需要改一下最后 r e t u r n return return 的值即可,那要怎么改呢?
在之前写的代码中,即使在数组中未找到该元素,那么 l l l 和 r r r 的值也都是有意义的, l l l 代表着数组中第一个大于目标值的元素, r r r 代表着第一个小于目标值的元素。
LeetCode题解:代码实现
LeetCode34. 在排序数组中查找元素的第一个和最后一个位置
难度:mid
你必须设计并实现时间复杂度为
O(log n)的算法解决此问题。
经典的二分问题,寻找左端点和右端点;这个题就是上面的二分查找—泛型情况。
首先写一个二分方法,找到目标值的开始位置,再利用小trick,使得一个方法既可以返回目标值的起始位置 也可以返回结束位置。
具体看题解代码及注释。
LeetCode题解:代码实现
LeetCode69. x 的平方根
难度:easy
典型的函数二分。
注意: 不允许使用任何内置指数函数和算符
所以我们只能使用迭代的方式。
这个题转换为公式: f ( x ) = x f(x)=\sqrt{x} f(x)=x,对这个函数进行二分。
LeetCode题解:代码实现
LeetCode475. 供暖器
难度:mid
如果这道题我们想要用二分来做的话,需要先对这两个数组进行排序。
我们可以先遍历所有的房屋,看看哪一个供暖器离它的距离最近(前面找一个供暖器,后面找一个供暖器,看看哪一个供暖器离我最近)
供暖器...房屋..供暖器 ← 像这种情况选择右面的供暖器
选择好之后,就可以认为加热半径就是这个距离。
那我们要怎么通过遍历来确定加热半径呢?
拿着房子的编号到加热器的编号中找
假设两个数组中的元素如图中所示,遍历 h o u s e s [ ] houses[\ ] houses[ ] 数组时,每一个值去 h e a t e r s [ ] heaters[\ ] heaters[ ] 数组中找,找哪一个值离它最近,对于 1 1 1 和 2 2 2 来说,找到后面离它最近的值,也就是第一个大于等于它的值,也就是 3 3 3,再将它们相减就得到了加热半径。
那么对于 4 4 4 来说,它的前后都有供暖器,所以需要找到最后一个小于它的值,和第一个大于等于它的值,再进行比较,对应图中的供暖器 3 3 3 和 5 5 5 都可以,再进行相减即可得到加热半径。
在进行寻找的过程中就可以使用二分查找。
最后在所有的加热半径中选择一个最大值就是这题的答案。
LeetCode题解:代码实现
经典面试题—复杂二分应用
LeetCode1. 两数之和
难度:easy
这道力扣的第一题也可以用二分来做,经典的 T w o S u m TwoSum TwoSum 问题。
因为要找出两数之和为 t a r g e t target target 的下标,我们换位思考,拿着 t a r g e t target target 去减数组中的数,然后在数组中寻找有没有这个差。
例如示例1,我们先拿着目标值 9 9 9 去减 2 2 2 等于 7 7 7,然后在数组中寻找有没有 7 7 7,如果没有再 9 − 7 = 2 9-7=2 9−7=2 去找数组中有没有 2 2 2,这样的寻找就可以使用二分查找。
如果我们要使用二分,前提必须保证它有序,但排完序后 每个数的下标就可能发生变化,无法正确返回原始下标,所以我们可以再开一个 i n d [ ] ind[\ ] ind[ ] 数组专门记录每一个元素的下标是多少,然后再根据原数组的大小进行排序 将新下标更新到 i n d [ ] ind[\ ] ind[ ] 数组中。
这道题可以用暴力 O ( N 2 ) O(N^2) O(N2)、哈希 O ( N ) O(N) O(N)、二分 O ( N log N ) O(N\log N) O(NlogN) 三个方法来做。
LeetCode题解:三种方法代码实现
LeetCode1658. 将 x 减到 0 的最小操作数
难度:mid
首先直接看这个题,是没法直接用二分来做的。
我们将这个问题转换一下,使用前缀和+后缀和,再进行观察:
原数组:1 1 4 2 3
前缀和:1 2 6 8 11 从左面删除1个..2个..3个..4个..5个
后缀和:11 10 9 5 3 从右面删除1个..2个..3个..4个..5个
假设我们选择从左面删除 1 1 1 个元素,此时目标值为 5 5 5,那么 5 − 1 = 4 5-1=4 5−1=4,从后缀和数组中找有没有 4 4 4 ,如果找到了代表这是一种方案,可以这么删;从右面删同理。
如果前缀和 或 后缀和有目标值 5 5 5,同样也是一种方案。
这样 就将这个题转换为了 T w o S u m TwoSum TwoSum 问题。
LeetCode题解:代码实现
LeetCode81. 搜索旋转排序数组 II
难度:mid
一个数组 在某一个下标进行了旋转,例如, [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] ,此时我们可以根据下标5对旋转后的数组进行分隔,变为:[4,5,6,6,7, | 0,1,2,4,4],此时我们发现,分隔后的这两段值,每一段仍然是具有单调性的,如下图所示:
所以这道题还是可以用二分来做,我们只需要注意 m i d mid mid 是出现在前半段还是在后半段。
LeetCode题解:代码实现
LeetCode1011. 在 D 天内送达包裹的能力
难度:mid
首先我们发现这个题的数组是有序的,那么很容易就想到用二分来做。
我们先确定二分的区间 [ l , r ] [l,\ r] [l, r],那么最小值 l l l 就是数组中最大的值,最大值 r r r 就是数组中所有的重量的累加。
实现一个 c h e c k ( ) check() check() 函数,返回当前载重运送所需要的天数。
基于函数进行二分。
LeetCode题解:代码实现
LeetCode4. 寻找两个正序数组的中位数
难度:hard
我们由求中位数,转换成求两个合并的正序数组的第 k k k 个数。
合并之后找的是第 k k k 个数,那么将两个数组拆开,就是分别找数组中的第 k 2 \frac{k}{2} 2k 个数。
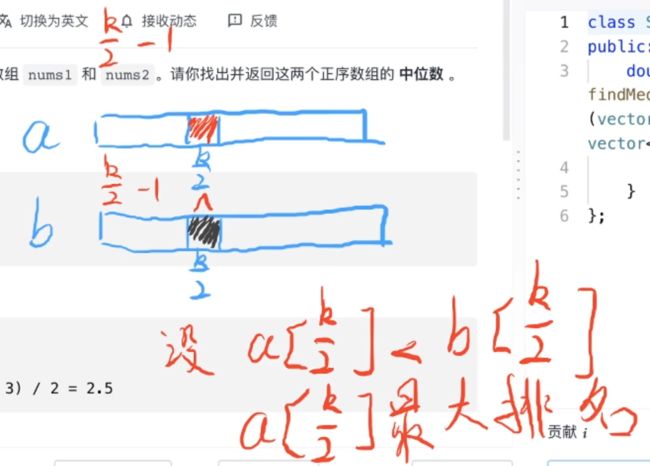
假设 a [ k 2 ] < b [ k 2 ] a[\frac{k}{2}] < b[\frac{k}{2}] a[2k]<b[2k],那么 a [ k 2 ] a[\frac{k}{2}] a[2k] 最多能排在第几位?
首先 a [ k 2 ] a[\frac{k}{2}] a[2k] 和 b [ k 2 ] b[\frac{k}{2}] b[2k] 前面值的个数都是 k 2 − 1 \frac{k}{2}-1 2k−1,合在一起就是 k − 2 k-2 k−2,所以 a [ k 2 ] a[\frac{k}{2}] a[2k] 的最大排名为 k − 1 k-1 k−1(最好的情况下)。
所以黄色部分就更不可能是第 k k k 个元素了:
所以我们可以把黄色部分和红色部分砍掉,因为它们永远到不了第 k k k 位,从而减少了区间范围。
如果 a [ k 2 ] < b [ k 2 ] a[\frac{k}{2}] < b[\frac{k}{2}] a[2k]<b[2k],那么就减少 a [ ] a[\ ] a[ ] 的部分,如果 a [ k 2 ] > b [ k 2 ] a[\frac{k}{2}] > b[\frac{k}{2}] a[2k]>b[2k],那么就减少 b [ ] b[\ ] b[ ] 的部分,哪边小就删哪边,不断减少范围。
LeetCode题解:代码实现
LeetCode300. 最长递增子序列
难度:mid
这道题是一道经典的DP问题,但也可以用贪心+二分来做,是时间复杂度最优的解法。
- 贪心思想:保证递增的子序列的最后一个数值尽量小,这样维护的一个子序列最终才会更长。
首先我们需要创建一个数组,记录我们的递增子序列。
逐一遍历原数组,并更新我们的递增子序列数组,如示例1:
10,9,2,5,3,7,101,18
遍历原数组 递增子序列数组中的值
10: 10 (直接放入10)
9: 9 (9比10小 所以直接替换10)
2: 2 (2比9小 所以直接替换9)
5: 2,5 (5比2大 所以可以放在2的后面)
3: 2,3 (3比5小 所以直接替换5)
7: 2,3,7 (7比3大 所以可以放在2,3的后面)
101: 2,3,7,101 (101比7大 所以可以放在2,3,7的后面)
18: 2,3,7,18 (8比101小 所以直接替换101 因为是贪心的思想 即使达到最大长度也会替换)
我们发现这道题用这种方式来思考,它就是一道 01 01 01 模型的题,找 01 01 01 模型中第一个 1 1 1 的位置,这个位置就是它的长度,我们不断更新这个长度,就可以得到一个最长的递增子序列。
LeetCode题解:两种方法代码实现 (dp、贪心 + 二分)
总结
二分其实是一个很大的概念,一般想到搜索的话,无非就是dfs、bfs和二分,其余的搜索基本都是这三种的变形。
而对于二分的模板来说,在这篇文章我大部分使用的都是
while (l <= r),而跟y总学习二分的时候使用的都是while (l < r),这两种模板看个人喜好,哪个好理解一点就用哪个。
二分一定要灵活的使用,不要死记模板,当然简单题一个模板就可以AC了,遇到复杂一点的题,适当变通一下 if else 的条件,也是可以做出来的。