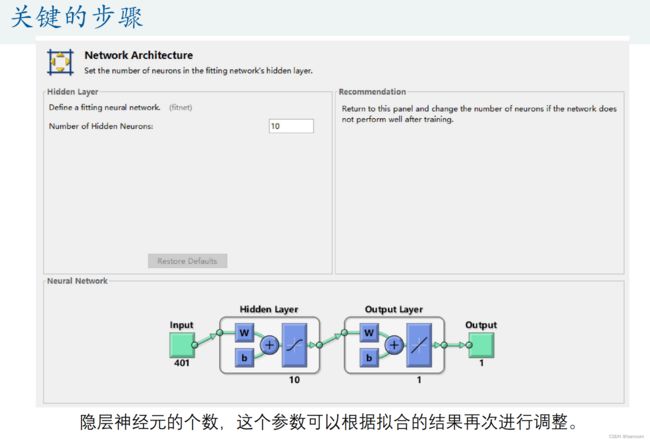
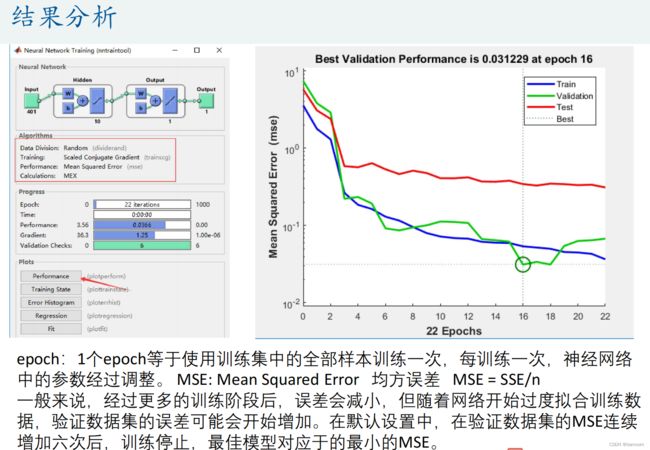
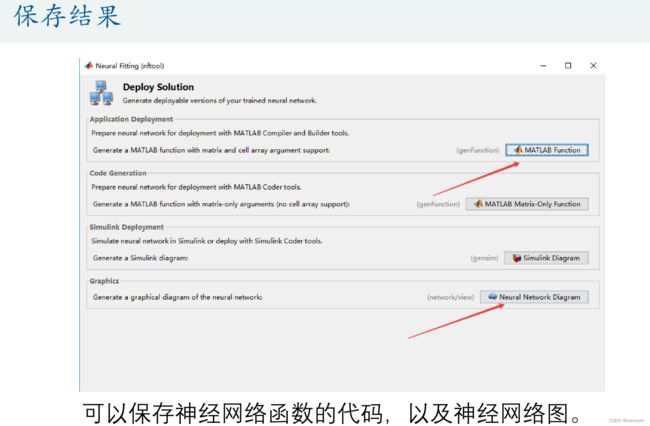
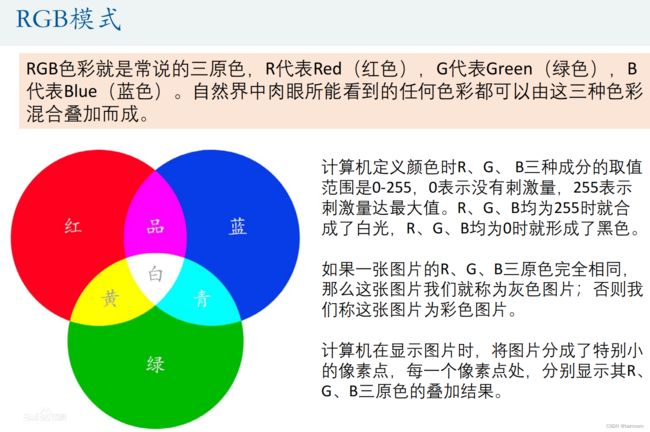
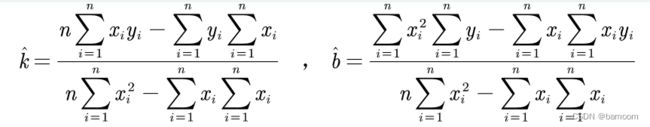数模艰辛之旅
2023.8.5更新
文章目录
- 1.层次分析法
-
- 评价类问题
-
- 一致性检验
- 计算权重
- 计算得分
- 总结
- 2.TOPSIS法(优劣解距离法)
-
-
- 统一指标类型(正向化)
- 标准化处理
-
- **标准化处理的计算公式**
- 计算得分
- 总结
-
- 3.插值算法
-
- 两种插值法的对比
- 艾尔米特插值
-
- 分段三次埃尔米特插值
- 三次样条插值
- n维数据的插值(了解)
- 4.拟合算法
-
- 最小二乘法的几何解释
-
- Matlab求解最小二乘
- 如何评价拟合的好坏
- 代码
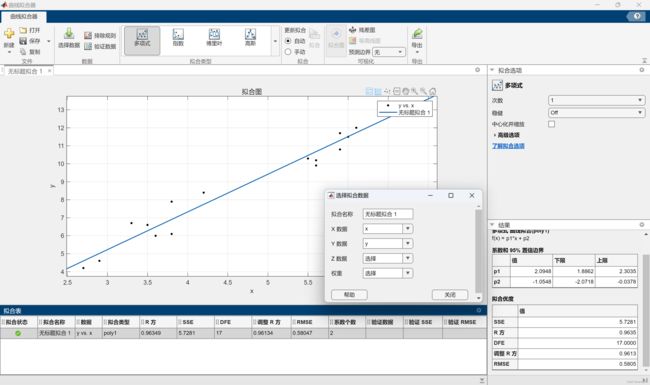
- 曲线拟合工具箱
- 5.相关系数
-
- 总体和样本
- 1.皮尔逊相关系数的计算以及数据的描述性统计
-
- 总体和样本皮尔逊Pearson相关系数
-
- 关于皮尔逊相关系数的一些理解误区
- 描述性统计
- 皮尔逊相关系数的计算
- 如何美化相关系数表
- 2.假设检验部分
-
- 对皮尔逊相关系数进行假设检验
-
- 总结
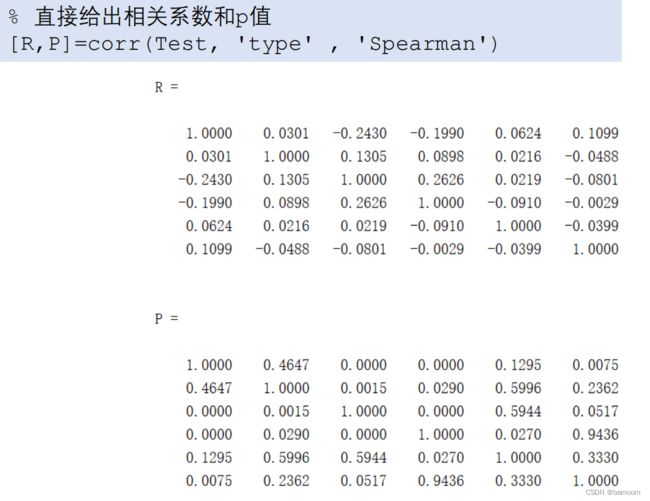
- 更好用的方法:p值判断法
- 3.皮尔逊相关系数假设检验
-
- 皮尔逊相关系数假设检验的条件
- 4.正态分布JB检验(大样本 n>30)
-
- 小样本3≤n≤50:Shapiro-wilk检验
- 小样本3≤n≤50:Q-Q图
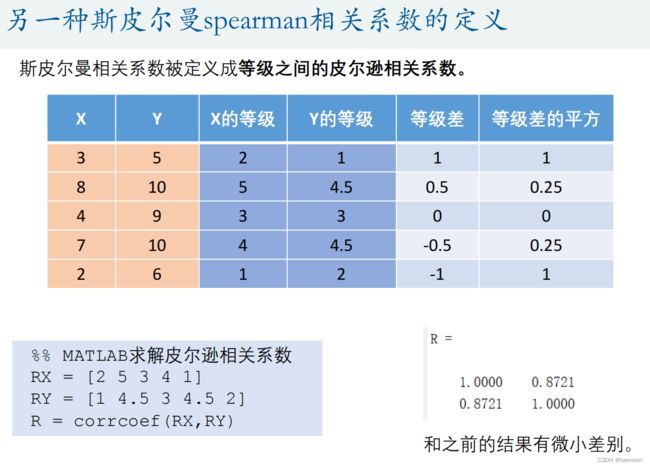
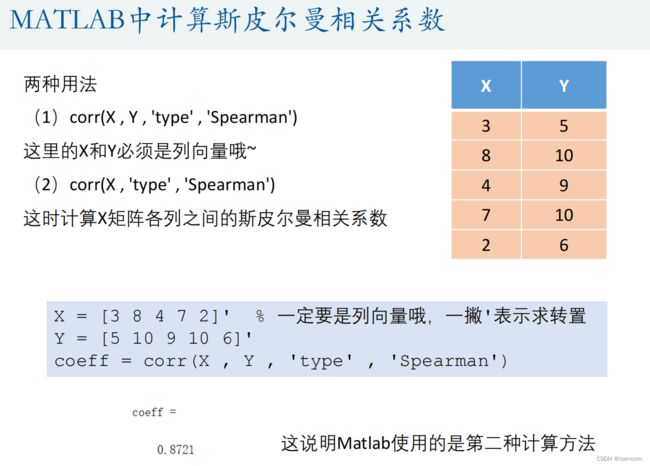
- 5.斯皮尔曼spearman相关系数
-
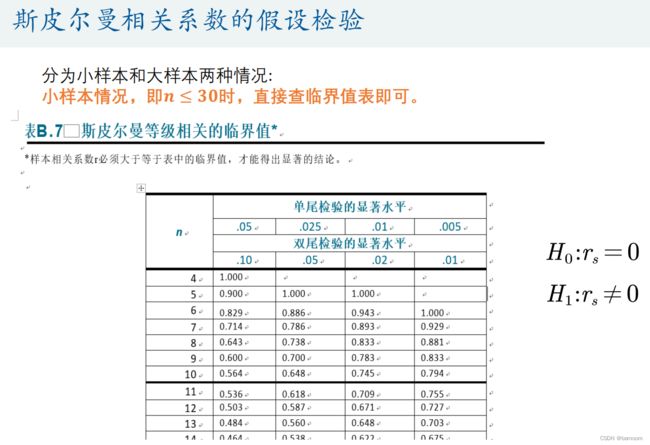
- 斯皮尔曼相关系数的假设检验
- 两个相关系数的比较:斯皮尔曼相关系数/皮尔逊相关系数:
- 6.典型相关分析
-
- 步骤
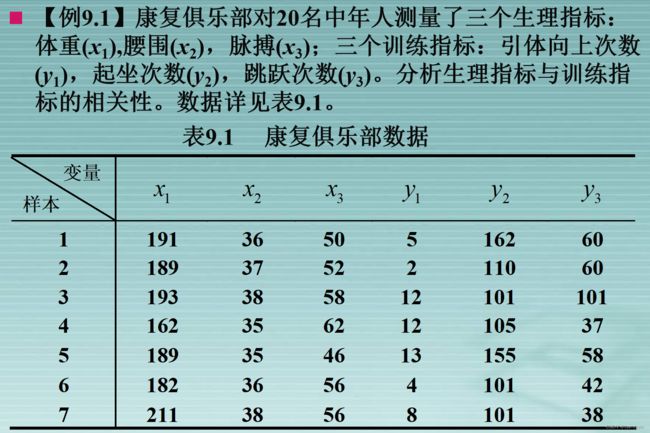
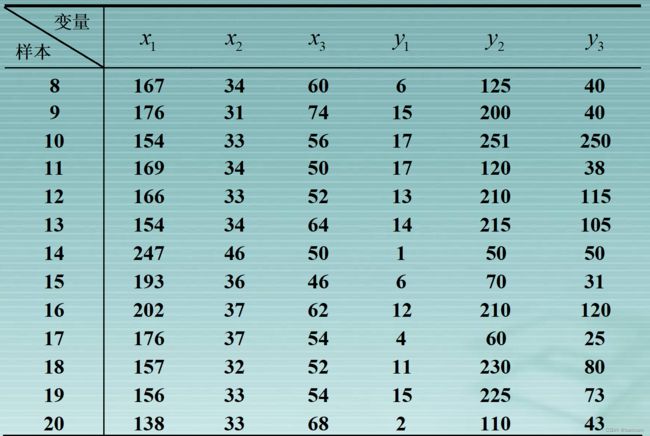
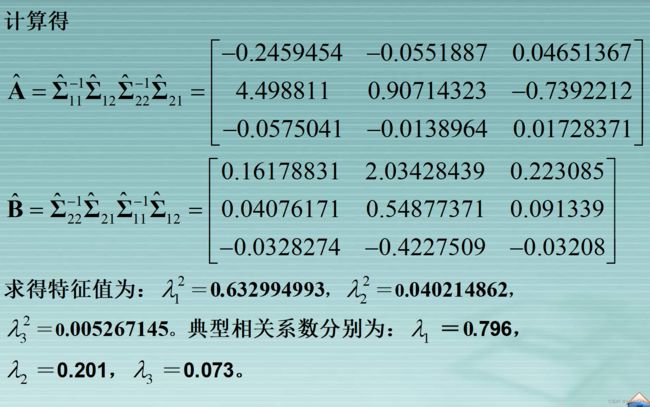
- 例题
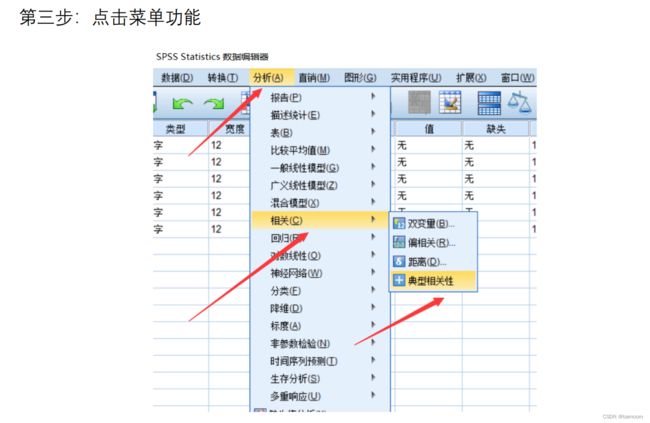
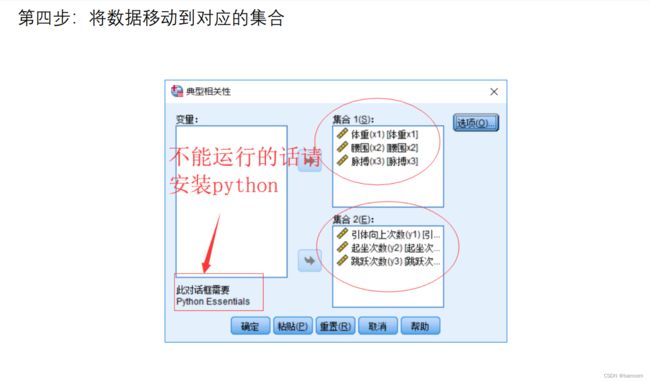
- spss软件操作
- 典型相关分析应用中的几个问题
-
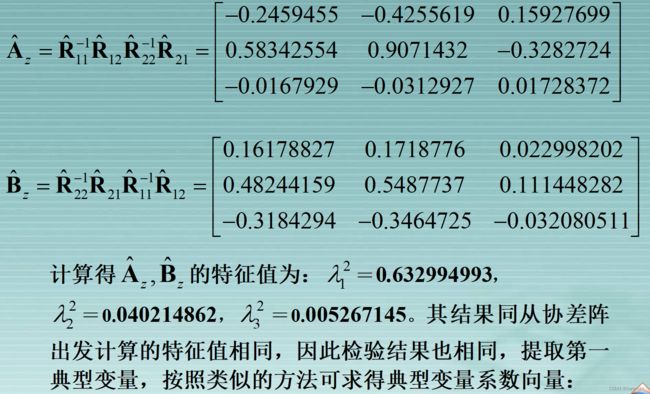
- 从相关矩阵出发计算典型相关
- 典型载荷分析
- 典型冗余分析
- 7.多元线性回归分析
-
- 1.回归分析的分类
- 2.数据
-
- 不同数据类型的处理方法
- 数据的收集
- 3.一元线性回归
-
- 回归系数的解释
- 内生性的蒙特卡罗模拟
- 4.四类模型回归系数的解释
- 5.特殊的自变量:虚拟变量X
-
- 多分类的虚拟变量设置
- 6.含有交互项的自变量
- 7.回归实例
-
- Stata软件
- 8.图论最短路径问题
-
- 作图
- 权重邻接矩阵
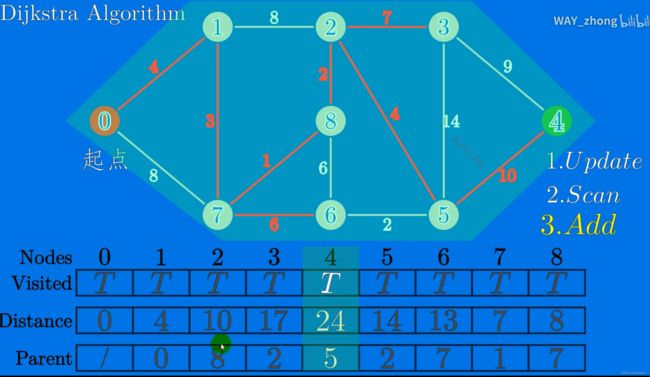
- 迪杰斯特拉算法
- Bellman‐Ford(贝尔曼‐福特)算法
- 负权回路
- Matlab计算最短路径
-
- ==返回任意两点的距离矩阵==
- ==找给定范围内所有的点==
- 9.分类模型
-
- 线性概率模型
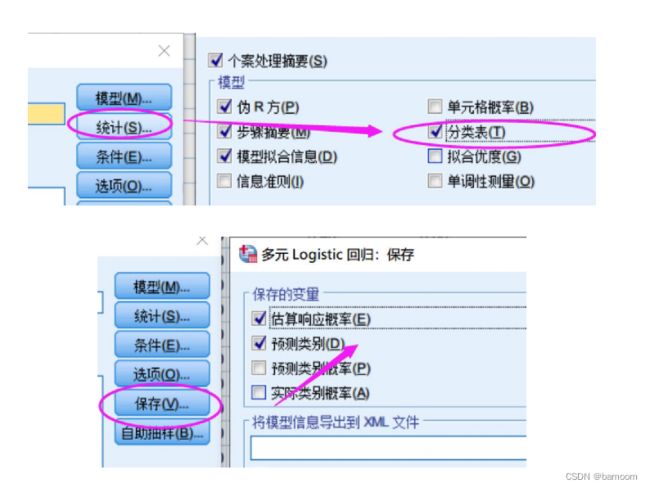
- Spss求解逻辑回归
-
- 过拟合现象
- 确定合适的模型——交叉验证
- Fisher线性判别分析
- 多分类问题
-
-
- Fisher判别分析
- Logistic回归
-
- 10.聚类模型
-
- K-means聚类算法
-
- Spss软件操作
- 系统(层次)聚类
-
- Spss软件操作
- 用图形估计聚类的数量
- DBSCAN算法
- 11.时间序列分析
-
- Spss处理时间序列中的缺失值
- SPSS中七种指数平滑方法的简单介绍
-
- Simple模型
- 线性趋势模型(linear trend)
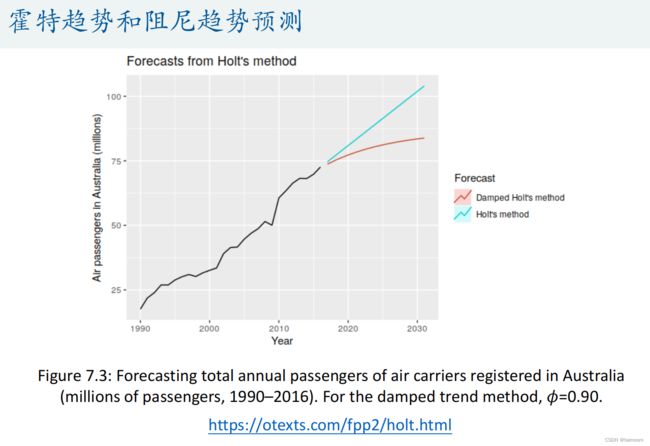
- 阻尼趋势模型(Damped trend)
- 简单季节性(Simple seasonal)
- 温特模型(Winters' additive)
- 一元时间序列分析的模型
-
- 时间序列的平稳性(stationary series)
- 差分方程
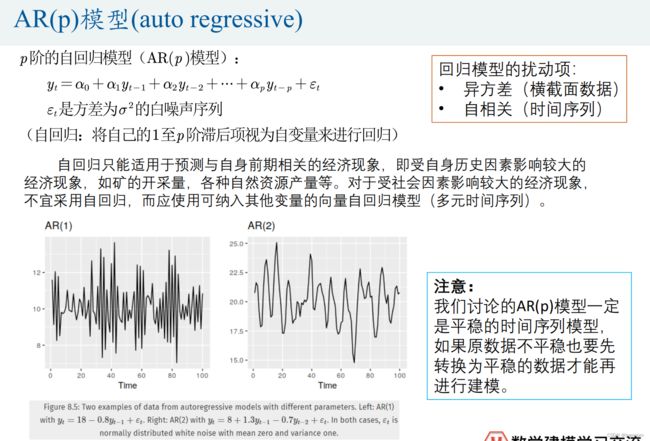
- AR(p )模型(auto regressive)
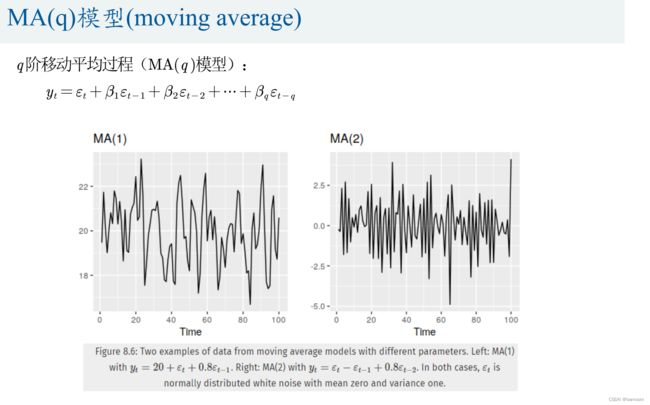
- MA(q)模型(moving average)
-
- MA模型和AR模型的关系
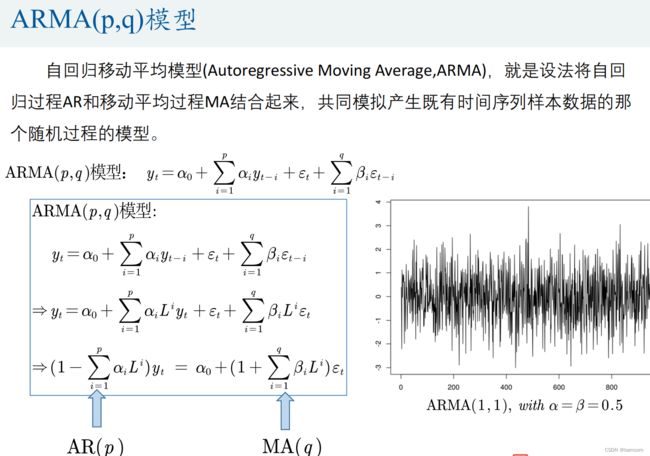
- ARMA(p,q)模型
- 模型选择:AIC和BIC准则(选小原则)
- Spss时间序列建模的思路
- 12.预测模型
-
- 灰色预测模型
-
- GM(1,1)模型: Grey(Gray) Model
- GM(1,1)模型的评价
- 灰色预测的例题
- BP神经网络预测
- 13.SVD和图形处理
-
- 奇异值分解
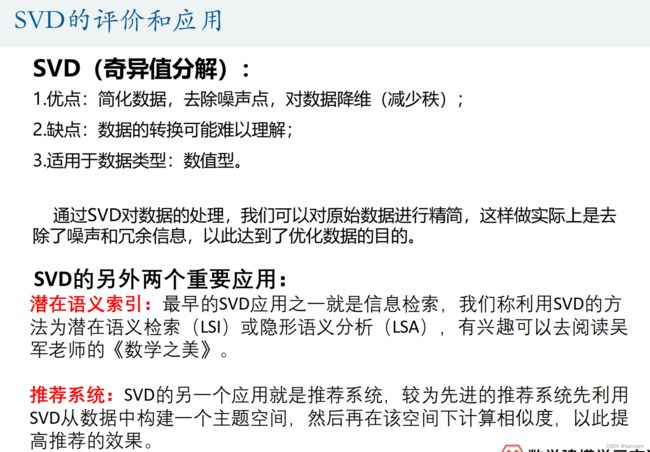
- SVD的评价和应用
- 14.主成分分析
-
- 数据降维
- 代码
- Spss聚类
1.层次分析法
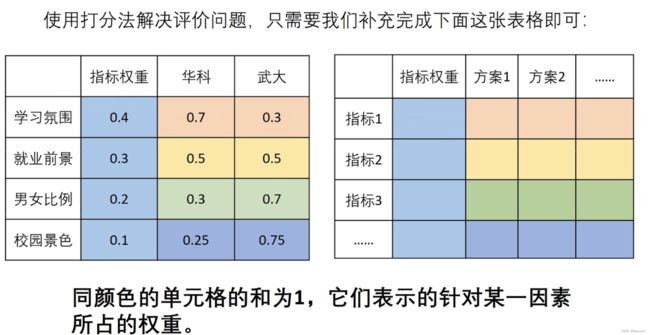
评价类问题
可以用打分解决
根据权重表格计算得分
如:高校对比,旅游选择
问题:请你确定评价指标、形成评价体系来为小明同学选择最佳的方案。
解决评价类问题,大家首先要想到以下三个问题:
-
①我们评价的目标是什么?
-
②我们为了达到这个目标有哪几种可选的方案?
-
③评价的准则或者说指标是什么?(我们根据什么东西来评价好坏)
-
- 去知网搜索论文
-
- 虫部落-快搜:https://search.chongbuluo.com/
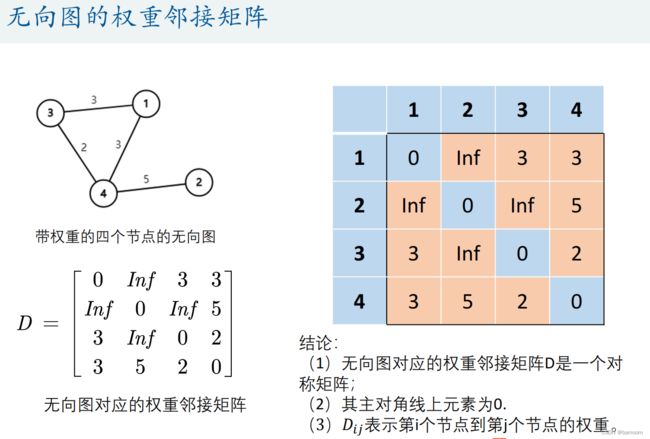
观察上面这两个矩阵的特点:各行(各列)之间成倍数关系
注意:在使用判断矩阵求权重之前,必须对其进行一致性检验。
一致性检验
- 原理:检验我们构造的判断矩阵和一致矩阵是否有太大的差别。
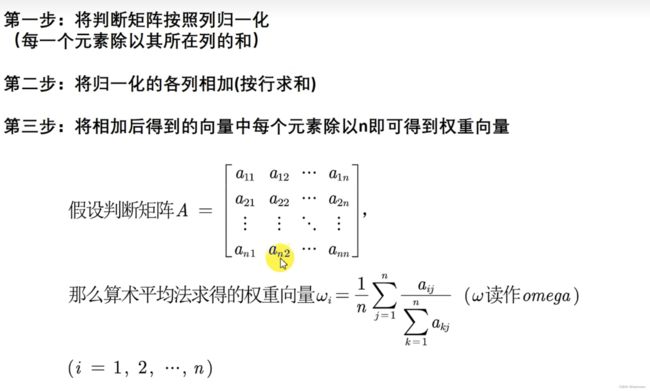
计算权重
一致矩阵怎么计算权重?
判断矩阵计算权重
计算得分
总结
使用ppt中smartart 作图
使用专业软件:亿图图示
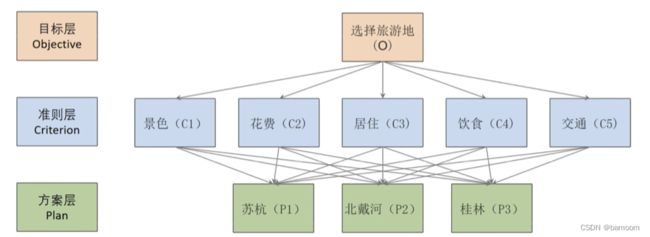
- 2.对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较,构造两两比较矩阵(判断矩阵)。(一般自己查资料给出)
- 3.由判断矩阵计算被比较元素对于该准则的相对权重并进行一致性检验(检验通过权重才能用).
三种方法计算权重:
(1)算术平均法(2)几何平均法(3)特征值法
强烈建议大家在比赛时三种方法都使用:
以往的论文利用层次分析法解决实际问题时,都是采用其中某一种方法求权重,而不同的计算方法可能会导致结果有所偏差。为了保证结果的稳健性,本文采用了三种方法分别求出了权重,再根据得到的权重矩阵计算各方案的得分,并进行排序和综合分析,这样避免了采用单一方法所产生的偏差,得出的结论将更全面、更有效
- 4.计算各层元素对系统目标的合成权重,并进行排序。
2.TOPSIS法(优劣解距离法)
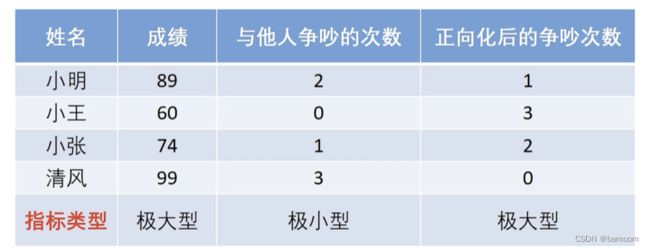
统一指标类型(正向化)
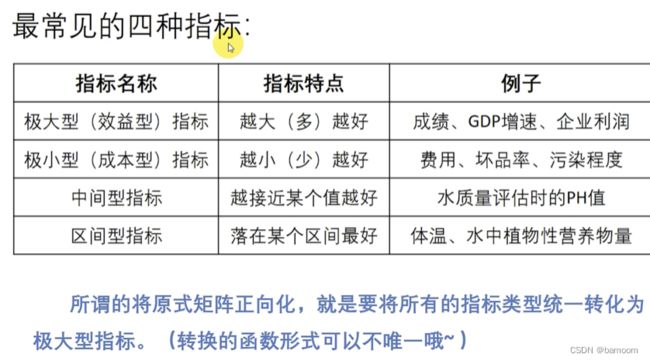
将所有的指标转化为极大型称为指标正向化(最常用)
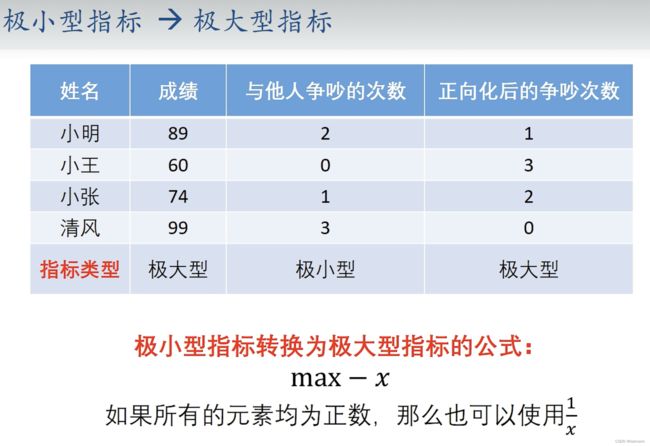
极小型指标转换为极大型指标的公式:max一x(推荐)。
如果所有的元素均为正数,那么也可以使用1/x。
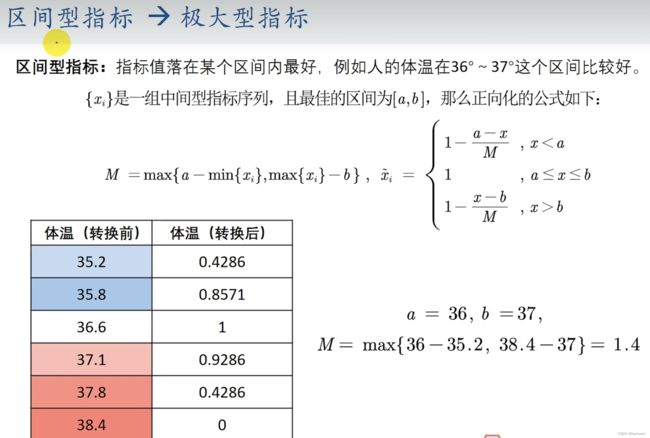
标准化处理
为了消去不同指标量纲的影响,需要对已经正向化的矩阵进行标准化处理

标准化处理的计算公式
/*标准化处理的计算公式*/
x=[89,1; 60,3; 74,2; 99, 0]
[n,m]=size (x)
x./repmat (sum (x. *x) .^ 0.5, n, 1)
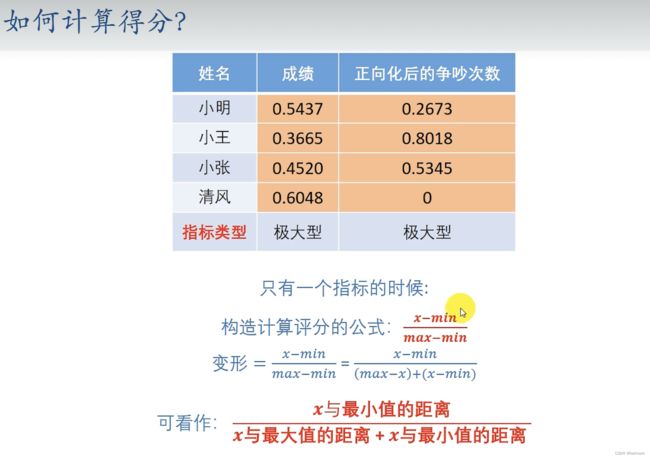
计算得分
总结
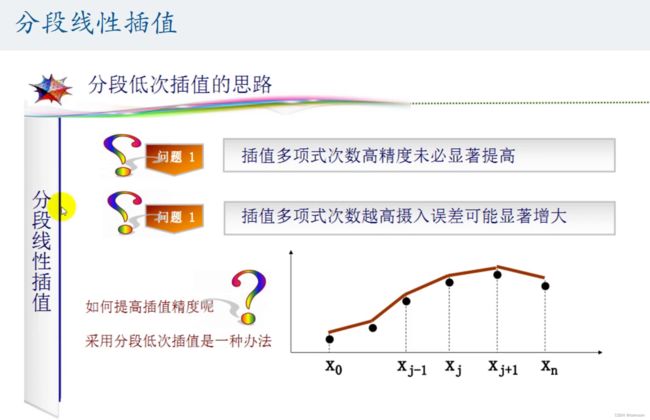
3.插值算法
数模比赛中,常常需要根据已知的函数点进行数据、模型的处理和分析,而有时候现有的数据是极少的,不足以支撑分析的进行,这时就需要使用一些数学的方法,“模拟产生”一些新的但又比较靠谱的值来满足需求,这就是插值的作用。
两种插值法的对比
-
缺点:与拉格朗日插值法相比,牛顿插值法的计算过程具有继承性。(牛顿插值法每次插值只和前n项的值有关,这样每次只要在原来的函数上添加新的项,就能够产生新的函数)但是牛顿插值也存在龙格现象的问题.
-
缺点:上面讲的两种插值仅仅要求插值多项式在插值节点处与被插函数有相等的函数值,而这种插值多项式却不能全面反映被插值函数的性态。然而在许多实际问题中,不仅要求插值函数与被插值函数在所有节点处有相同的函数值,它也需要在一个或全部节点上插值多项式与被插函数有相同的低阶甚至高阶的导数值。对于这些情况,拉格朗日插值和牛顿插值都不能满足。
龙格现象:
高次插值会产生龙格现象,即在两端处波动极大,产生明显的震荡。在不熟悉曲线
运动趋势的前提下,不要轻易使用高次插值
艾尔米特插值
不但要求在节点上的函数值相等,而且还要求对应的导数值也相等,甚至要求高阶导数也相等,满足这种要求的插值多项式就是埃尔米特插值多项式。

分段三次埃尔米特插值
直接使用Hermite插值得到的多项式次数较高,也存在着龙格现象,因此在实际应用中,往往使用分段三次 Hermite 插值多项式 (PCHIP)。
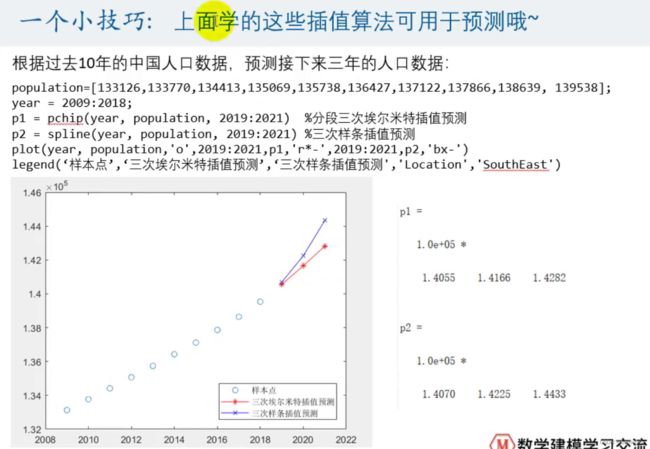
Matlab有内置的函数(实现过程已经帮我们封装好了,会调用就行了):p = pchip(x,y,new_x)
x是已知的样本点的横坐标;y是已知的样本点的纵坐标;new_x是要插入处对应的横坐标
% 分段三次埃尔米特插值
x = -pi:pi; y = sin(x);
new_x = -pi:0.1:pi;
p = pchip(x,y,new_x);
figure(1); % 在同一个脚本文件里面,要想画多个图,需要给每个图编号,否则只会显示最后一个图哦~
plot(x, y, 'o', new_x, p, 'r-')
% plot函数用法:
% plot(x1,y1,x2,y2)
% 线方式: - 实线 :点线 -. 虚点线 - - 波折线
% 点方式: . 圆点 +加号 * 星号 x x形 o 小圆
% 颜色: y黄; r红; g绿; b蓝; w白; k黑; m紫; c青
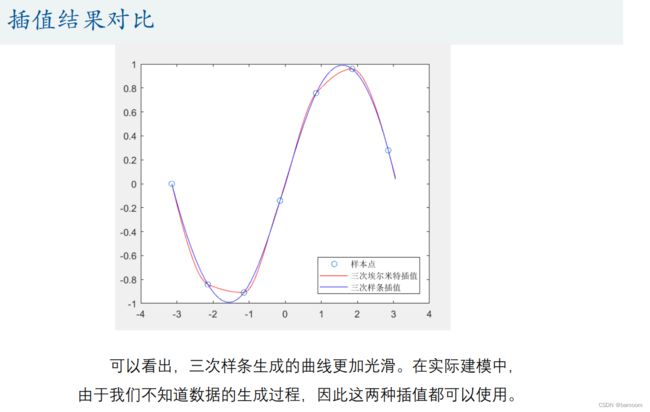
三次样条插值
Matlab有内置的函数:p = spline (x,y, new_x)
x是已知的样本点的横坐标;y是已知的样本点的纵坐标;new_x是要插入处对应的横坐标
% 三次样条插值和分段三次埃尔米特插值的对比
x = -pi:pi;
y = sin(x);
new_x = -pi:0.1:pi;
p1 = pchip(x,y,new_x); %分段三次埃尔米特插值
p2 = spline(x,y,new_x); %三次样条插值
figure(2);
plot(x,y,'o',new_x,p1,'r-',new_x,p2,'b-')
legend('样本点','三次埃尔米特插值','三次样条插值','Location','SouthEast') %标注显示在东南方向
% 说明:
% LEGEND(string1,string2,string3, …)
% 分别将字符串1、字符串2、字符串3……标注到图中,每个字符串对应的图标为画图时的图标。
% ‘Location’用来指定标注显示的位置
n维数据的插值(了解)
% n维数据的插值
x = -pi:pi; y = sin(x);
new_x = -pi:0.1:pi;
p = interpn (x, y, new_x, 'spline');
% 等价于 p = spline(x, y, new_x);
figure(3);
plot(x, y, 'o', new_x, p, 'r-')
4.拟合算法
插值和拟合的区别
- 插值算法:得到的多项式f(x)要经过所有样本点。但是如果样本点太多,那么这个多项式次数过高,会造成龙格现象。
- 在拟合问题:不需要曲线一定经过给定的点。拟合问题的目标是寻求一个函数(曲线),使得该曲线在某种准则下与所有的数据点最为接近,即曲线拟合的最好(最小化损失函数)。

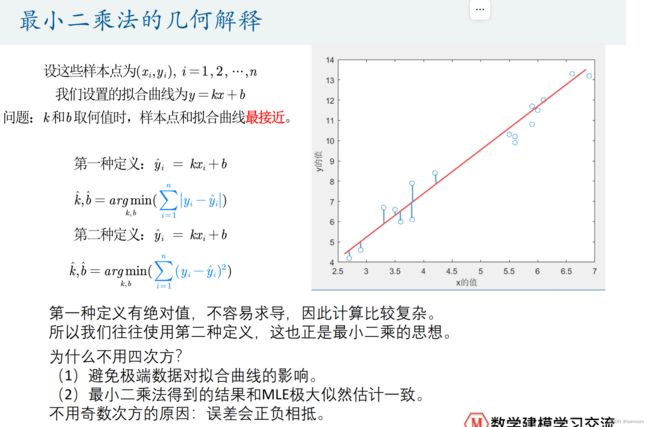
最小二乘法的几何解释
Matlab求解最小二乘
k = (n*sum(x.*y)-sum(x)sum(y))/(nsum(x.*x)-sum(x)*sum(x))
b = (sum(x.*x)*sum(y)-sum(x)*sum(x.y))/(nsum(x.*x)-sum(x)*sum(x))
如何评价拟合的好坏
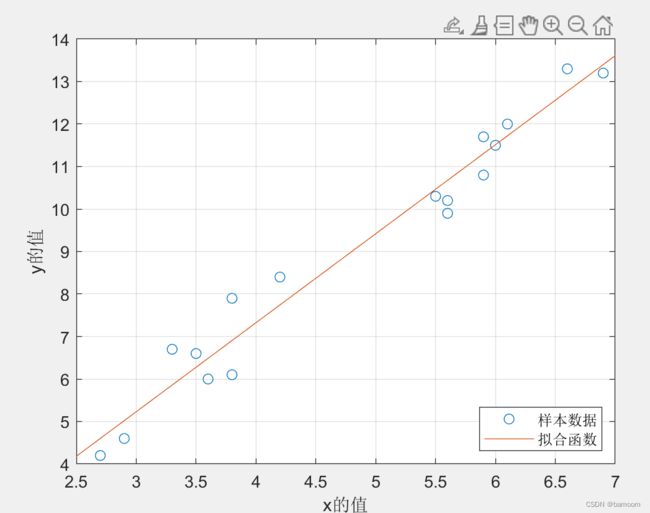
代码
clear;clc
load data1
plot(x,y,'o')
% 给x和y轴加上标签
xlabel('x的值')
ylabel('y的值')
n = size(x,1);
k = (n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x))
b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x))
hold on % 继续在之前的图形上来画图形
grid on % 显示网格线
% % 画出y=kx+b的函数图像 plot(x,y)
% % 传统的画法:模拟生成x和y的序列,比如要画出[0,5]上的图形
% xx = 2.5: 0.1 :7 % 间隔设置的越小画出来的图形越准确
% yy = k * xx + b % k和b都是已知值
% plot(xx,yy,'-')
% 匿名函数的基本用法。
% handle = @(arglist) anonymous_function
% 其中handle为调用匿名函数时使用的名字。
% arglist为匿名函数的输入参数,可以是一个,也可以是多个,用逗号分隔。
% anonymous_function为匿名函数的表达式。
% 举个小例子
% z=@(x,y) x^2+y^2;
% z(1,2)
% % ans = 5
% fplot函数可用于画出匿名一元函数的图形。
% fplot(f,xinterval) 将匿名函数f在指定区间xinterval绘图。xinterval = [xmin xmax] 表示定义域的范围
f=@(x) k*x+b;
fplot(f,[2.5,7]);
legend('样本数据','拟合函数','location','SouthEast')
y_hat = k*x+b; % y的拟合值
SSR = sum((y_hat-mean(y)).^2) % 回归平方和
SSE = sum((y_hat-y).^2) % 误差平方和
SST = sum((y-mean(y)).^2) % 总体平方和
SST-SSE-SSR % 5.6843e-14 = 5.6843*10^-14 matlab浮点数计算的一个误差
R_2 = SSR / SST
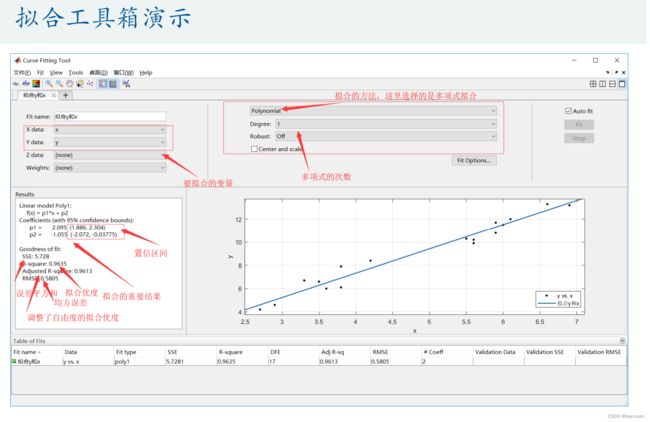
曲线拟合工具箱
5.相关系数
本讲我们将介绍两种最为常用的相关系数:皮尔逊pearson相关系数和斯皮尔曼spearman等级相关系数。它们可用来衡量两个变量之间的相关性的大小,根据数据满足的不同条件,我们要选择不同的相关系数进行计算和分析(建模论文中最容易用错的方法)。
总体和样本
- 总体——所要考察对象的全部个体叫做总体.我们总是希望得到总体数据的一些特征(例如均值方差等)
- 样本——从总体中所抽取的一部分个体叫做总体的一个样本.
计算这些抽取的样本的统计量来估计总体的统计量:
例如使用样本均值、样本标准差来估计总体的均值(平均水平)和总体的标准差(偏离程度)。
例子:
我国10年进行一次的人口普查得到的数据就是总体数据。
大家自己在QQ群发问卷叫同学帮忙填写得到的数据就是样本数据
1.皮尔逊相关系数的计算以及数据的描述性统计
总体和样本皮尔逊Pearson相关系数
关于皮尔逊相关系数的一些理解误区
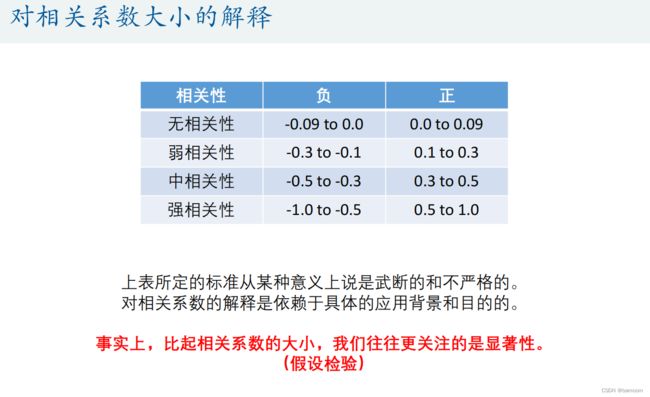
这里的相关系数只是用来衡量两个变量线性相关程度的指标;
也就是说,你必须先确认这两个变量是线性相关的,然后这个相关系数才能告诉你他俩相关程度如何。
小结
(1)如果两个变量本身就是线性的关系,那么皮尔逊相关系数绝对值大的就是相关性强,小的就是相关性弱;
(2)在不确定两个变量是什么关系的情况下,即使算出皮尔逊相关系数,发现很大,也不能说明那两个变量线性相关,甚至不能说他们相关,我们一定要先画出散点图来看才行。
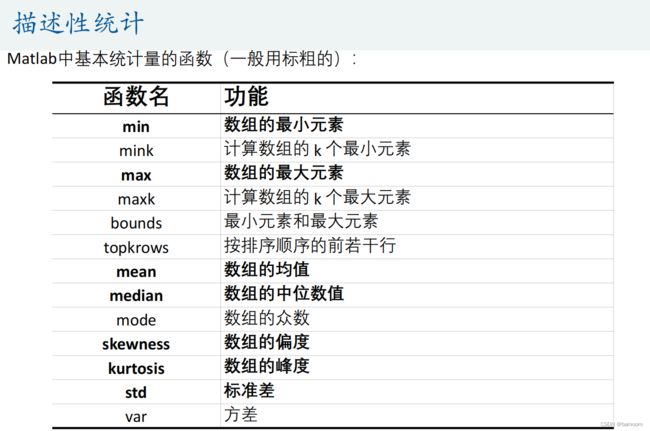
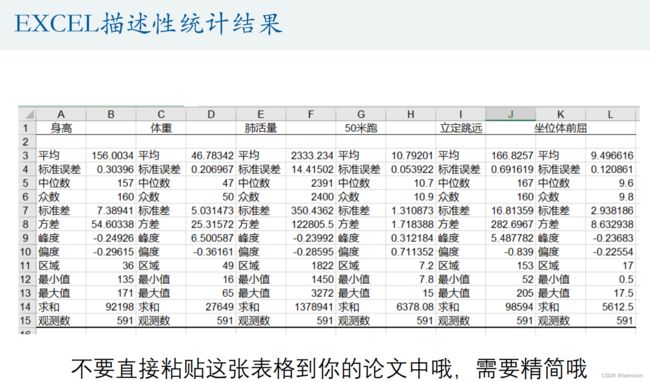
描述性统计
clear;clc
load 'physical fitness test.mat' %文件名如果有空格隔开,那么需要加引号
% https://ww2.mathworks.cn/help/matlab/ref/corrcoef.html
%% 统计描述
MIN = min(Test); % 每一列的最小值
MAX = max(Test); % 每一列的最大值
MEAN = mean(Test); % 每一列的均值
MEDIAN = median(Test); %每一列的中位数
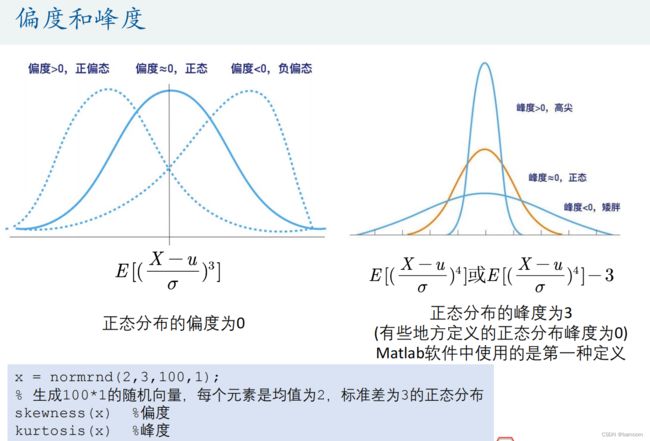
SKEWNESS = skewness(Test); %每一列的偏度
KURTOSIS = kurtosis(Test); %每一列的峰度
STD = std(Test); % 每一列的标准差
%将这些统计量放到一个矩阵中表示
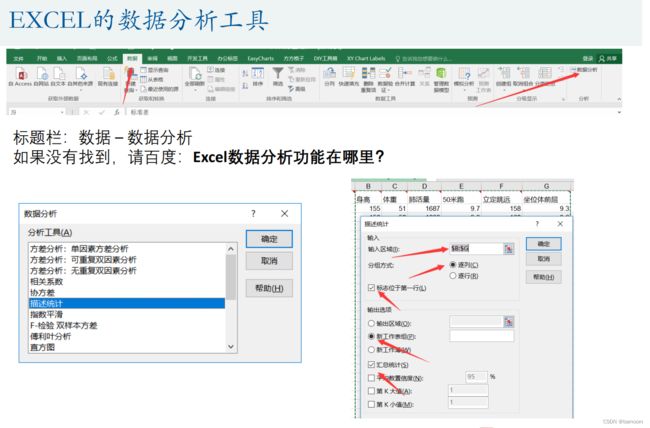
皮尔逊相关系数的计算
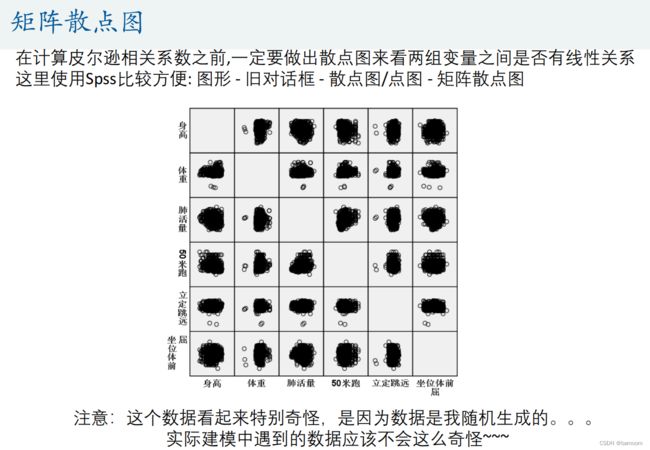
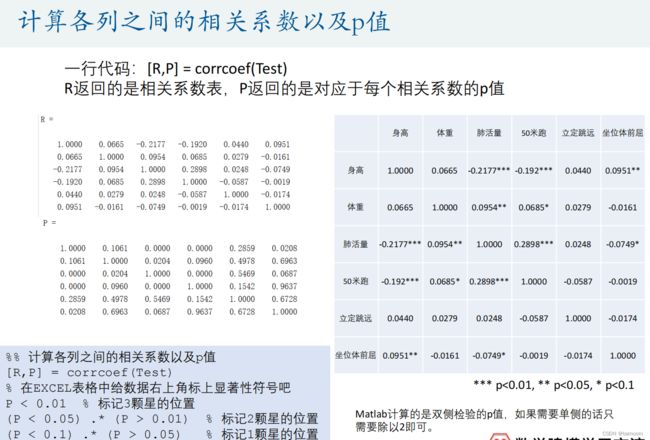
这里使用Spss比较方便: 图形 - 旧对话框 - 散点图/点图 - 矩阵散点图
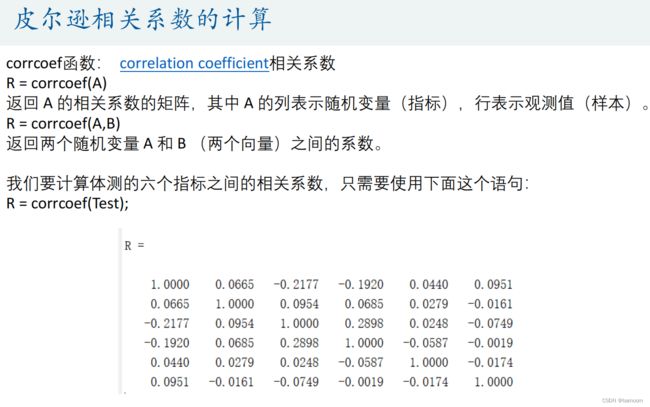
corrcoef函数: correlation coefficient相关系数
R = corrcoef(A)
%% 计算各列之间的相关系数
% 在计算皮尔逊相关系数之前,一定要做出散点图来看两组变量之间是否有线性关系
% 这里使用Spss比较方便: 图形 - 旧对话框 - 散点图/点图 - 矩阵散点图
R = corrcoef(Test) % correlation coefficient
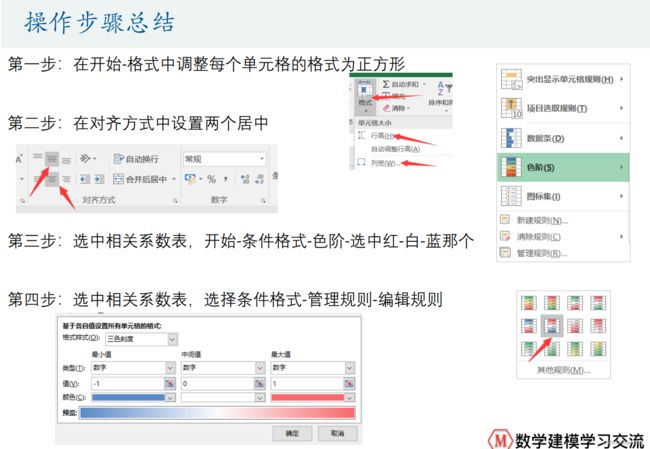
如何美化相关系数表
2.假设检验部分
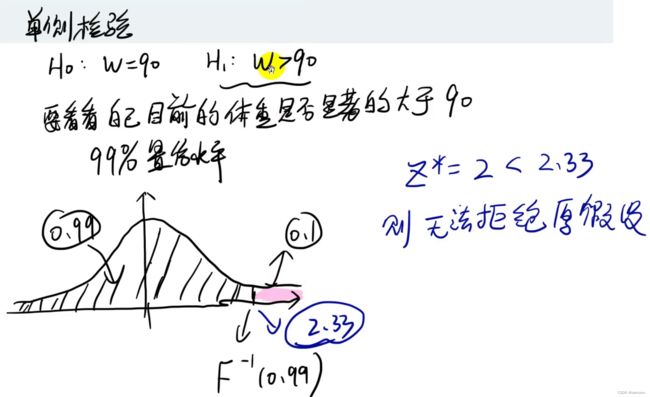
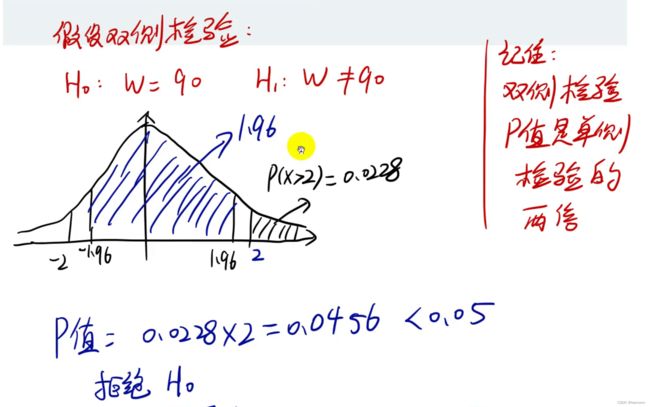
对皮尔逊相关系数进行假设检验
总结
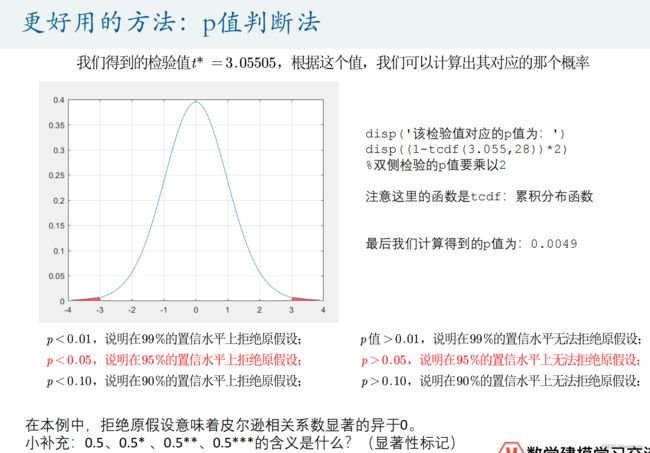
更好用的方法:p值判断法
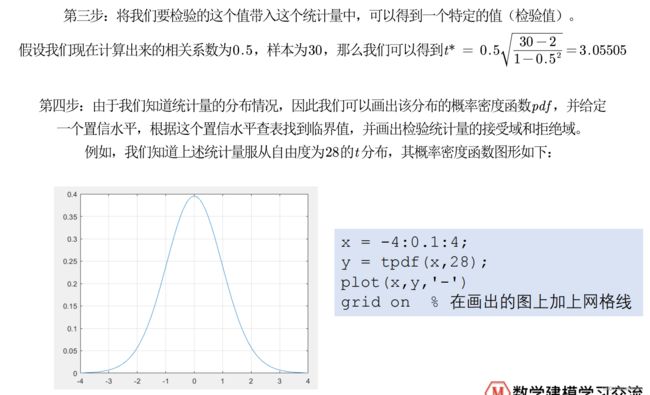
3.皮尔逊相关系数假设检验
t分布表:
https://wenku.baidu.com/view/d94dbd116bd97f192279e94a.html
皮尔逊相关系数假设检验的条件
- 第一, 实验数据通常假设是成对的来自于正态分布的总体。因为我们在求皮尔逊相关性系数以后,通常还会用t检验之类的方法来进行皮尔逊相关性系数检验,而t检验是基于数据呈正态分布的假设的。
- 第二, 实验数据之间的差距不能太大。皮尔逊相关性系数受异常值的影响比较大。
- 第三:每组样本之间是独立抽样的。构造t统计量时需要用到。
4.正态分布JB检验(大样本 n>30)
小样本3≤n≤50:Shapiro-wilk检验
小样本3≤n≤50:Q-Q图
在统计学中,Q‐Q图(Q代表分位数Quantile)是一种通过比较两个概率分布的分位数对这两个概率分布进行比较的概率图方法。首先选定分位数的对应概率区间集合,在此概率区间上,点(x,y)对应于第一个分布的一个分位数x和第二个分布在和x相同概率区间上相同的分位数。
这里,我们选择正态分布和要检验的随机变量,并对其做出QQ图,可想而知,如果要检验的随机变量是正态分布,那么QQ图就是一条直线。要利用Q‐Q图鉴别样本数据是否近似于正态分布,只需看Q‐Q图上的点是否近似地在一条直线附近。(要求数据量非常大)。

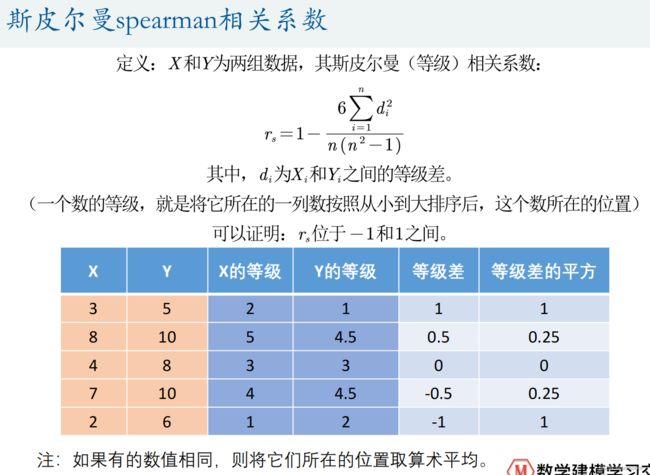
5.斯皮尔曼spearman相关系数
斯皮尔曼相关系数的假设检验
两个相关系数的比较:斯皮尔曼相关系数/皮尔逊相关系数:
6.典型相关分析
典型相关分析(Canonical Correlation analysis)
研究两组变量(每组变量中都可能有多个指标)之间相关关系的一种多元统计方法。它能够揭示出两组变量之间的内在联系。
温馨提示:这一讲涉及到多元统计的知识,如果对原理听不懂也没关系,等以后学完了主成分分析模型后再回过头来看比较合适。
- 典型相关分析的定义
- 典型相关分析由Hotelling提出,其基本思想和主成分分析非常相似。
- 首先在每组变量中找出变量的线性组合,使得两组的线性组合之间具有最大的相关系数;
- 然后选取和最初挑选的这对线性组合不相关的线性组合,使其配对,并选取相关系数最大的一对;
- 如此继续下去,直到两组变量之间的相关性被提取完毕为止。
- 被选出的线性组合配对称为典型变量,它们的相关系数称为典型相关系数。典型相关系数度量了这两组变量之间联系的强度。

步骤
(1)数据的分布有假设:两组数据服从联合正态分布。
![]() (2)首先要对两组变量的相关性进行检验(构造似然比统计量 )。
(2)首先要对两组变量的相关性进行检验(构造似然比统计量 )。
p值小于0.05(0.1)表示在95%(90%)的置信水平下拒绝原假设,即认为两组变量有关。

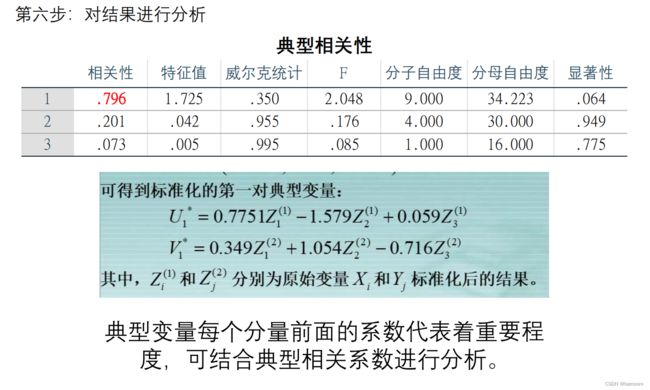
(3)确定典型相关变量的个数(直接看典型相关系数对应的P值即可)
 (4)利用标准化后的典型相关变量分析问题
(4)利用标准化后的典型相关变量分析问题
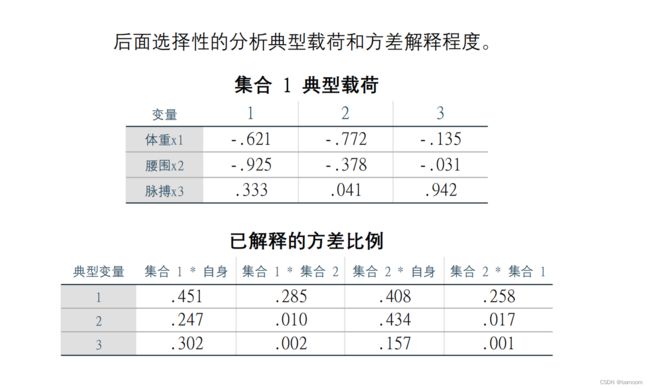
(5)进行典型载荷分析

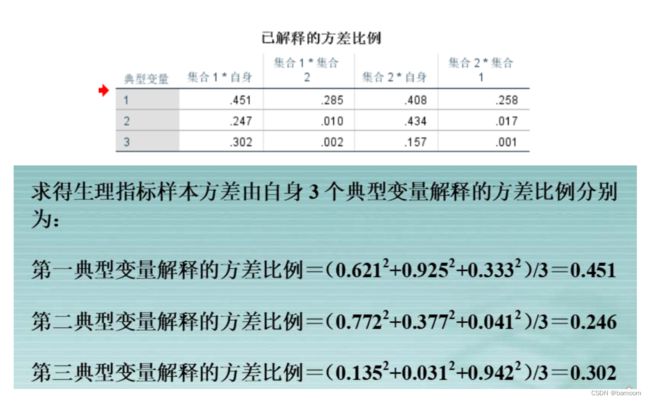
(6)计算前 r个典型变量对样本总方差的贡献
例题
spss软件操作
典型相关分析应用中的几个问题
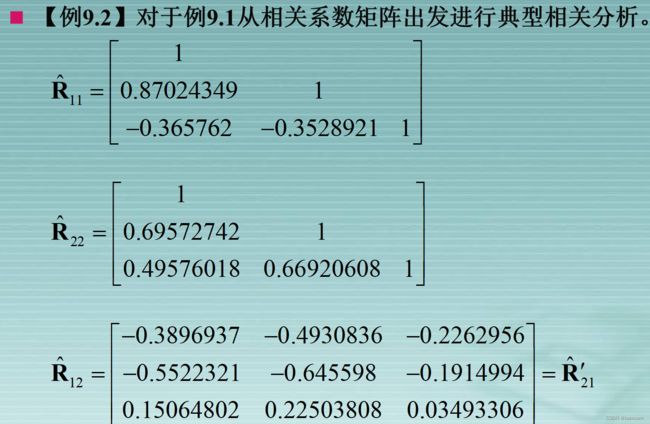
典型相关分析涉及多个变量,不同的变量往往具有不同的量纲及不同的数量级别。在进行典型相关分析时,由于典型变量是原始变量的线性组合,具有不同量纲变量的线性组合显然失去了实际意义。其次,不同的数量级别会导致“以大吃小”,即数量级别小的变量的影响会被忽略,从而影响了分析结果的合理性。因此,为了消除量纲和数量级别的影响,必须对数据先做标准化变换处理,然后再做典型相关分析.显然,经标准化变换之后的协差阵就是相关系数矩阵,因而,也即通常应从相关矩阵出发进行典型相关分析。
从相关矩阵出发计算典型相关
典型载荷分析
典型冗余分析
7.多元线性回归分析
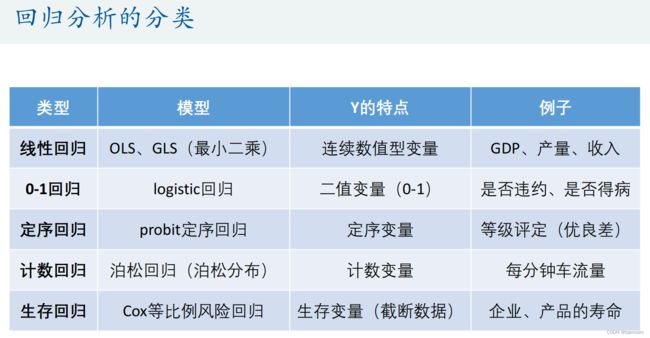
- 回归分析是数据分析中最基础也是最重要的分析工具,绝大多数的数据分析问题,都可以使用回归的思想来解决。回归分析的任务就是,通过研究自变量X和因变量Y的相关关系,尝试去解释Y的形成机制,进而达到通过X去预测Y的目的。
- 常见的回归分析有五类:线性回归、0‐1回归、定序回归、计数回归和生存回归,其划分的依据是因变量Y的类型。本讲我们主要学习线性回归。
回归分析:研究X和Y之间相关性的分析。
三个关键词
- 相关性
- Y
- X
1.相关性 ≠ 因果性
在绝大多数情况下,我们没有能力去探究严格的因果关系,所以只好退而求其次,改成通过回归分析,研究相关关系。
2.Y是什么?俗称因变量。
取义,因为别人的改变,而改变的变量。在实际应用中,Y常常是我们需要研究的那个核心变量。
(1)经济学家研究经济增长的决定因素,那么Y可以选取GDP增长率(连续数值型变量)。
(2)P2P公司要研究借款人是否能按时还款,那么Y可以设计成一个二值变量,Y=0时代表可以还款,Y=1时代表不能还款(0‐1型变量)。
(3)消费者调查得到的数据(1表示非常不喜欢,2表示有点不喜欢,3表示一般般,4表示有点喜欢,5表示非常喜欢)(定序变量)。
(4)管理学中RFM模型:F代表一定时间内,客户到访的次数,次数其实就是一个非负的整数。(计数变量)
(5)研究产品寿命、企业寿命甚至是人的寿命(这种数据往往不能精确的观测,例如现在要研究吸烟对于寿命的影响,如果选取的样本中老王60岁,现在还活的非常好,我们不可能等到他去世了再做研究,那怎么办呢?直接记他的寿命为60+,那这种数据就是截断的数据)(生存变量)
3.X是用来解释Y的相关变量,所以X被称为自变量。Y是因变量(因为别人的改变,而改变的变量)。
当然,另一套定义方法是:X为解释变量,Y为被解释变量。
回归分析的任务就是,通过研究X和Y的相关关系,尝试去解释Y的形成机制,进而达到通过X去预测Y的目的。
1.回归分析的分类
2.数据
不同数据类型的处理方法
1.横截面数据:在某一时点收集的不同对象的数据。
例如:
(1)我们自己发放问卷得到的数据
(2)全国各省份2018年GDP的数据
(3)大一新生今年体测的得到的数据
2.时间序列数据:对同一对象在不同时间连续观察所取得的数据。
例如:
(1)从出生到现在,你的体重的数据(每年生日称一次)。
(2)中国历年来GDP的数据。
(3)在某地方每隔一小时测得的温度数据。
3.面板数据:横截面数据与时间序列数据综合起来的一种数据资源。
例如:
2008‐2018年,我国各省份GDP的数据。

数据的收集
上面的数据多半都是宏观数据,微观数据市面上很少
大家可以在人大经济论坛搜索: https://bbs.pinggu.org/
另外也可以自己学习爬虫
(1)Python等软件爬取(需要编程基础,实际学习起来不困难)
网易云课堂:零基础21天搞定Python分布爬虫
(2)傻瓜式软件爬取(八爪鱼)
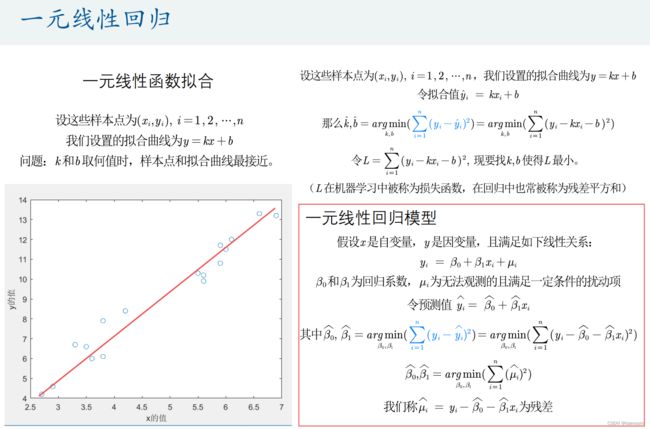
3.一元线性回归
回归系数的解释
1.包含了所有与y相关,但未添加到回归模型中的变量.如果这些变量和我们已经添加的自变量相关,则存在内生性
.
2.如果满足误差项μ和所有的自变量x均不相关,则称该回归模型具有外生性(如果相关,则存在内生性,内生性会导致回归系数估计的不准确:不满足无偏和一致性)
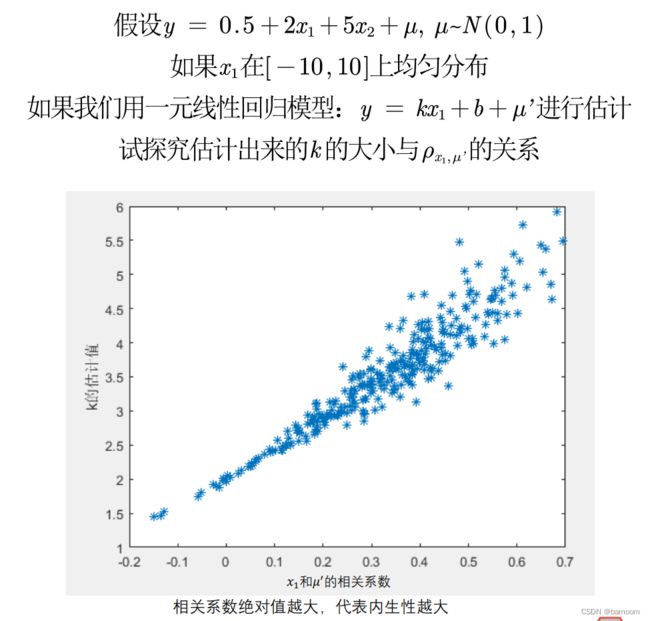
内生性的蒙特卡罗模拟
%% 蒙特卡洛模拟:内生性会造成回归系数的巨大误差
times = 300; % 蒙特卡洛的次数
R = zeros(times,1); % 用来储存扰动项u和x1的相关系数
K = zeros(times,1); % 用来储存遗漏了x2之后,只用y对x1回归得到的回归系数
for i = 1: times
n = 30; % 样本数据量为n
x1 = -10+rand(n,1)*20; % x1在-10和10上均匀分布,大小为30*1
u1 = normrnd(0,5,n,1) - rand(n,1); % 随机生成一组随机数
x2 = 0.3*x1 + u1; % x2与x1的相关性不确定, 因为我们设定了x2要加上u1这个随机数
% 这里的系数0.3我随便给的,没特殊的意义,你也可以改成其他的测试。
u = normrnd(0,1,n,1); % 扰动项u服从标准正态分布
y = 0.5 + 2 * x1 + 5 * x2 + u ; % 构造y
k = (n*sum(x1.*y)-sum(x1)*sum(y))/(n*sum(x1.*x1)-sum(x1)*sum(x1)); % y = k*x1+b 回归估计出来的k
K(i) = k;
u = 5 * x2 + u; % 因为我们回归中忽略了5*x2,所以扰动项要加上5*x2
r = corrcoef(x1,u); % 2*2的相关系数矩阵
R(i) = r(2,1);
end
plot(R,K,'*')
xlabel("x_1和u'的相关系数")
ylabel("k的估计值")
4.四类模型回归系数的解释
5.特殊的自变量:虚拟变量X
多分类的虚拟变量设置
6.含有交互项的自变量
7.回归实例
Stata软件
(1)定量数据
summarize 变量1 变量2 … 变量n
(2)定性数据
tabulate 变量名,gen(A)
返回对应的这个变量的频率分布表,并生成对应的虚拟变量(以A开头)
8.图论最短路径问题
本讲将简要介绍图论中的基本概念,并主要讲解图论中的最短路径问题。根据图的不同,我们将学习两种不同的算法:迪杰斯特拉Dijkstra算法和Bellman‐Ford(贝尔曼‐福特)算法。
作图
1.在线做图: https://csacademy.com/app/graph_editor/
2.Matlab作图

%% 注意:以下代码需要较新版本的matlab才能运行(最好是2016版本及以上哦)
% 如果运行出错请下载新版的matlab代码再运行
%% Matlab作无向图
% (1)无权重(每条边的权重默认为1)
% 函数graph(s,t):可在 s 和 t 中的对应节点之间创建边,并生成一个图
% s 和 t 都必须具有相同的元素数;这些节点必须都是从1开始的正整数,或都是字符串元胞数组。
s1 = [1,2,3,4];
t1 = [2,3,1,1];
G1 = graph(s1, t1);
plot(G1)
% 注意哦,编号最好是从1开始连续编号,不要自己随便定义编号
s1 = [1,2,3,4];
t1 = [2,3,1,1];
G1 = graph(s1, t1);
plot(G1)
% 注意字符串元胞数组是用大括号包起来的哦
s2 = {'学校','电影院','网吧','酒店'};
t2 = {'电影院','酒店','酒店','KTV'};
G2 = graph(s2, t2);
plot(G2, 'linewidth', 2) % 设置线的宽度
% 下面的命令是在画图后不显示坐标
set( gca, 'XTick', [], 'YTick', [] );
% (2)有权重
% 函数graph(s,t,w):可在 s 和 t 中的对应节点之间以w的权重创建边,并生成一个图
s = [1,2,3,4];
t = [2,3,1,1];
w = [3,8,9,2];
G = graph(s, t, w);
plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2)
set( gca, 'XTick', [], 'YTick', [] );
%% Matlab作有向图
% 无权图 digraph(s,t)
s = [1,2,3,4,1];
t = [2,3,1,1,4];
G = digraph(s, t);
plot(G)
set( gca, 'XTick', [], 'YTick', [] );
% 有权图 digraph(s,t,w)
s = [1,2,3,4];
t = [2,3,1,1];
w = [3,8,9,2];
G = digraph(s, t, w);
plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2)
set( gca, 'XTick', [], 'YTick', [] );
权重邻接矩阵
迪杰斯特拉算法
Bellman‐Ford(贝尔曼‐福特)算法
- 事实上,贝尔曼‐福特算法不再将节点区分为是否已访问的状态,因为贝尔曼‐福特模型是利用循环来进行更新权重的,且每循环一次,贝尔曼福特算法都会更新所有的节点的信息。
- 贝尔曼‐福特算法不支持含有负权回路的图。(视频中提到的Floyd(弗洛伊德)算法也不可以)
负权回路
Matlab计算最短路径
%% 注意:以下代码需要较新版本的matlab才能运行(最好是2016版本及以上哦)
% 如果运行出错请下载新版的matlab代码再运行
% 注意哦,Matlab中的图节点要从1开始编号,所以这里把0全部改为了9
% 编号最好是从1开始连续编号,不要自己随便定义编号
s = [9 9 1 1 2 2 2 7 7 6 6 5 5 4];
t = [1 7 7 2 8 3 5 8 6 8 5 3 4 3];
w = [4 8 3 8 2 7 4 1 6 6 2 14 10 9];
G = graph(s,t,w);
plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2)
set( gca, 'XTick', [], 'YTick', [] );
[P,d] = shortestpath(G, 9, 4) %注意:该函数matlab2015b之后才有哦
% 在图中高亮我们的最短路径
myplot = plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2); %首先将图赋给一个变量
highlight(myplot, P, 'EdgeColor', 'r') %对这个变量即我们刚刚绘制的图形进行高亮处理(给边加上r红色)
% 求出任意两点的最短路径矩阵
D = distances(G) %注意:该函数matlab2015b之后才有哦
D(1,2) % 1 -> 2的最短路径
D(9,4) % 9 -> 4的最短路径
% 找出给定范围内的所有点 nearest(G,s,d)
% 返回图形 G 中与节点 s 的距离在 d 之内的所有节点
[nodeIDs,dist] = nearest(G, 2, 10) %注意:该函数matlab2016a之后才有哦
返回任意两点的距离矩阵
找给定范围内所有的点
9.分类模型
本讲将介绍分类模型。对于二分类模型,我们将介绍逻辑回归(logistic regression)和Fisher线性判别分析两种分类算法;对于多分类模型,我们将简单介绍Spss中的多分类线性判别分析和多分类逻辑回归的操作步骤。


线性概率模型
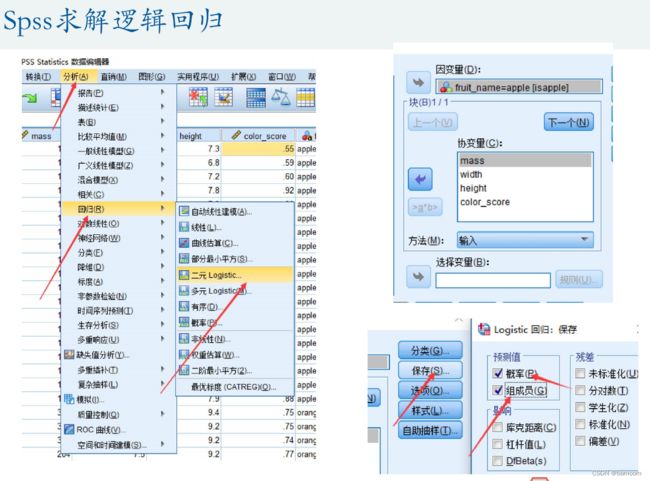
Spss求解逻辑回归
过拟合现象
确定合适的模型——交叉验证
Fisher线性判别分析
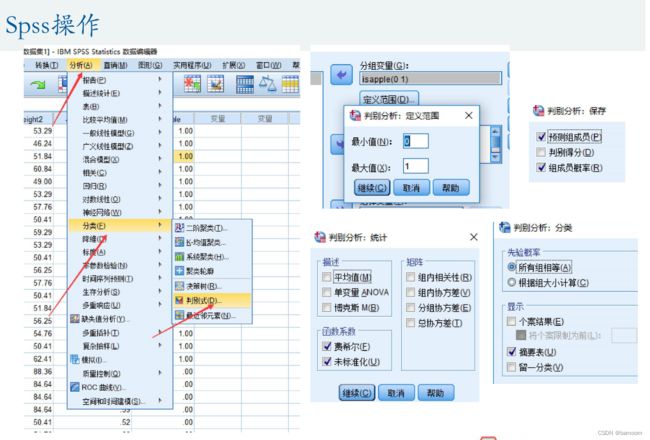
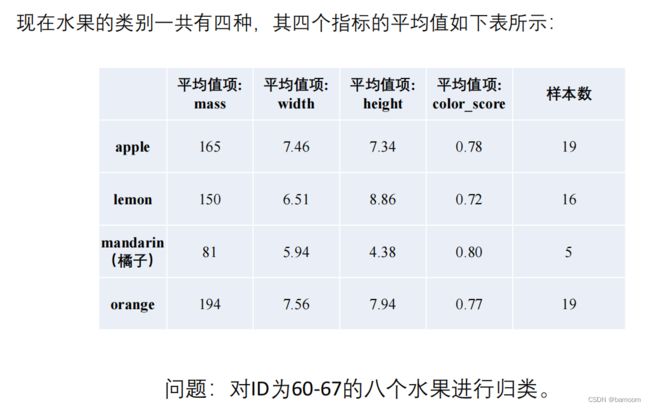
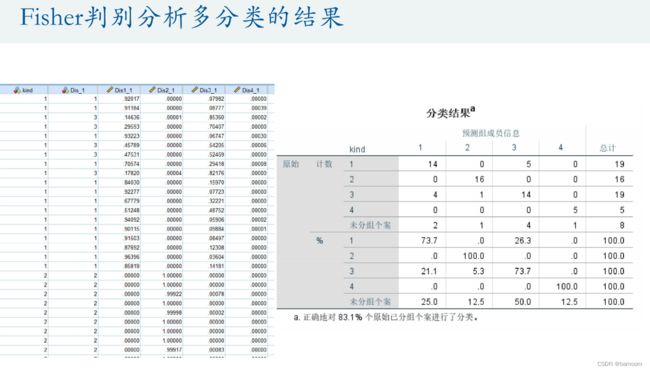
多分类问题
Fisher判别分析
Logistic回归
10.聚类模型
“物以类聚,人以群分”,所谓的聚类,就是将样本划分为由类似的对象组成的多个类的过程。聚类后,我们可以更加准确的在每个类中单独使用统计模型进行估计、分析或预测;也可以探究不同类之间的相关性和主要差异。
聚类和上一讲分类的区别:分类是已知类别的,聚类未知。
K-means聚类算法
K-means聚类的算法流程:
一、指定需要划分的簇[cù]的个数K值(类的个数);
二、随机地选择K个数据对象作为初始的聚类中心(不一定要是我们的样本点);
三、计算其余的各个数据对象到这K个初始聚类中心的距离,把数据对象划归到距离它最近的那个中心所处在的簇类中;
四、调整新类并且重新计算出新类的中心;
五、循环步骤三和四,看中心是否收敛(不变),如
果收敛或达到迭代次数则停止循环;
六、结束。
K-means算法的评价
优点:
(1)算法简单、快速。
(2)对处理大数据集,该算法是相对高效率的。
缺点:
(1)要求用户必须事先给出要生成的簇的数目K。
(2)对初值敏感。
(3)对于孤立点数据敏感。
Spss软件操作
先描述性统计,进行标准化
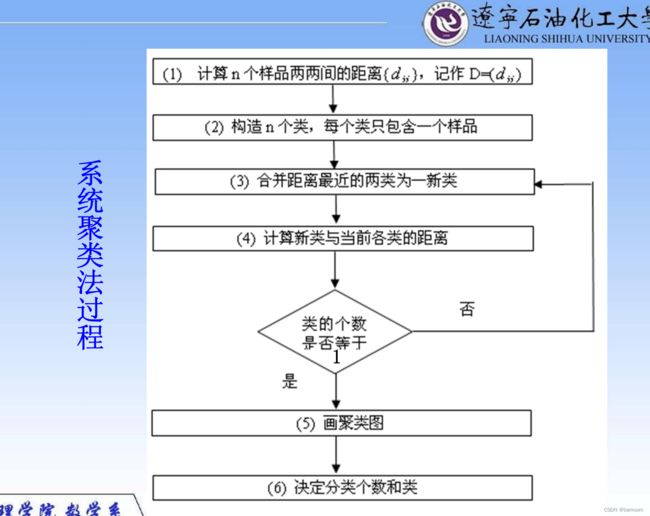
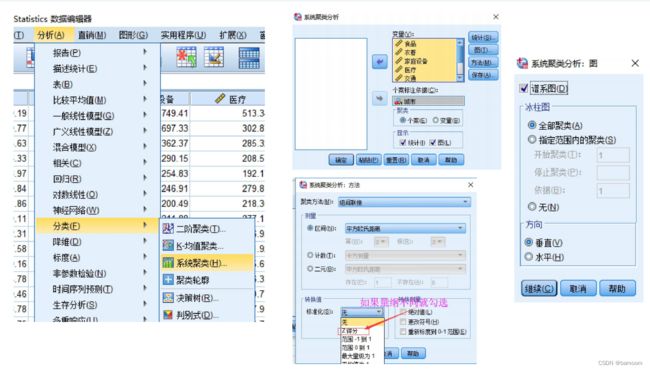
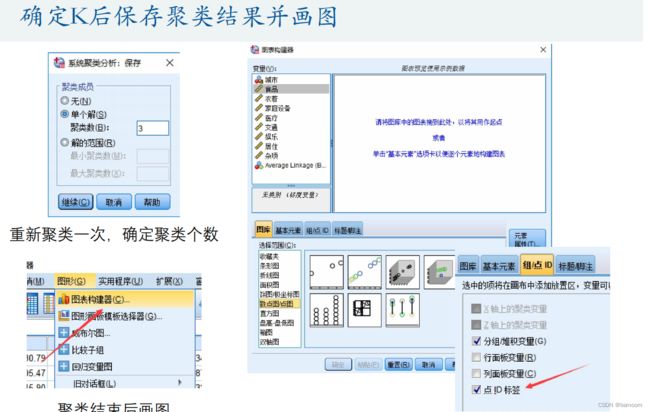
系统(层次)聚类
系统聚类的合并算法通过计算两类数据点间的距离,对最为接近的两类数据点进行组合,并反复迭代这一过程,直到将所有数据点合成一类,并生成聚类谱系图
系统(层次)聚类的算法流程:
一、将每个对象看作一类,计算两两之间的最小距离;
二、将距离最小的两个类合并成一个新类;
三、重新计算新类与所有类之间的距离;
四、重复二三两步,直到所有类最后合并成一类;
五、结束。
聚类分析需要注意的问题
1.对于一个实际问题要根据分类的目的来选取指标,指标选取的不同分类结果一般也不同。
2.样品间距离定义方式的不同,聚类结果一般也不同。
3.聚类方法的不同,聚类结果一般也不同(尤其是样品特别多的时候)。最好能通过各种方法找出其中的共性。
4.要注意指标的量纲,量纲差别太大会导致聚类结果不合理。
5.聚类分析的结果可能不令人满意,因为我们所做的是一个数学的处理,对于结果我们要找到一个合理的解释.
Spss软件操作
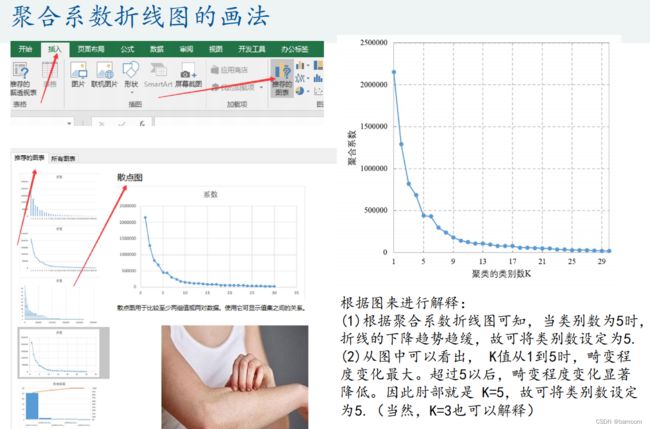
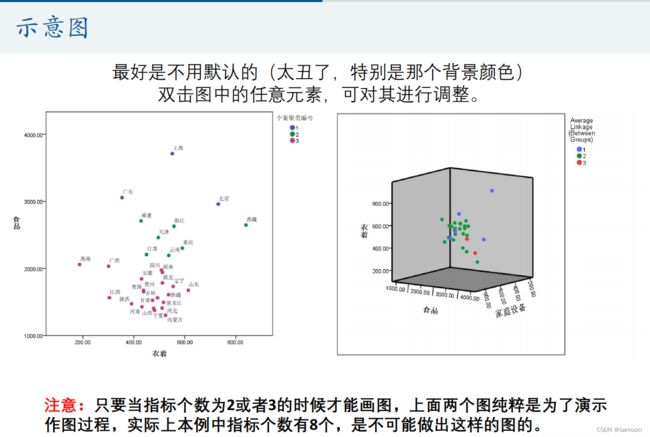
用图形估计聚类的数量
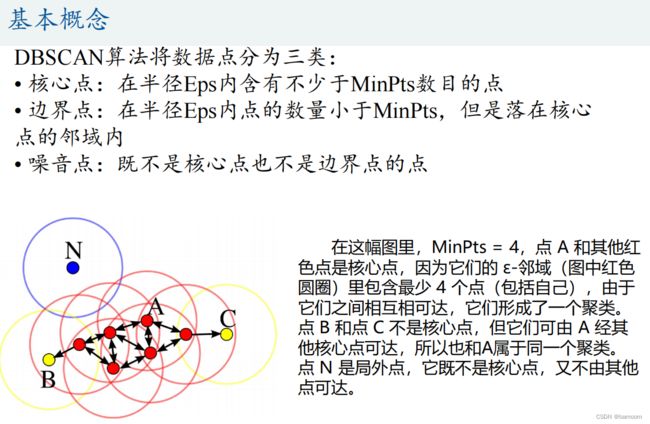
DBSCAN算法
该算法利用基于密度的聚类的概念,即要求聚类空间中的一定区域内所包含对象(点或其他空间对象)的数目不小于某一给定阈值。
该方法能在具有噪声的空间数据库中发现任意形状的簇,可将密度足够大的相邻区域连接,能有效处理异常数据。
DBSCAN算法可视化
https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/
11.时间序列分析
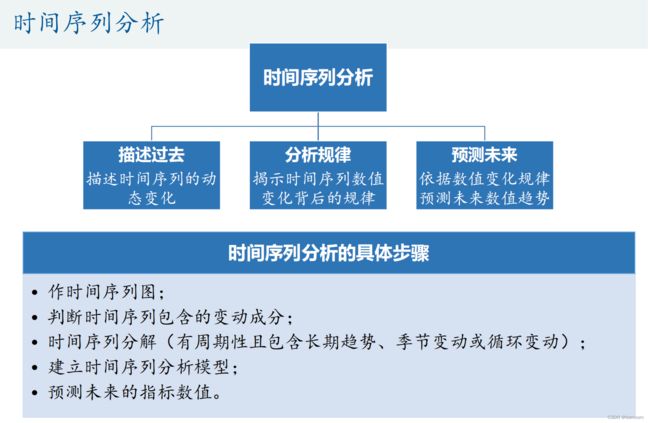
时间序列也称动态序列,是指将某种现象的指标数值按照时间顺序排列而成的数值序列。时间序列分析大致可分成三大部分,分别是描述过去、分析规律和预测未来,本讲主要介绍时间序列分析中常用的三种模型:季节分解、指数平滑方法和ARIMA模型,并将结合Spss软件对时间序列数据进行建模。


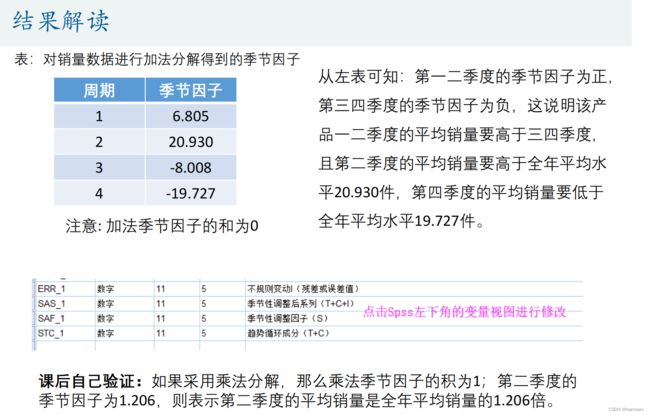
时间序列分解
-
长期趋势:T
- 例如,随着国家经济的发展,人均收入将逐渐提升;随着医学
水平的提高,新生儿死亡率在不断下降。
- 例如,随着国家经济的发展,人均收入将逐渐提升;随着医学
-
季节趋势:S
- 百度指数:http://index.baidu.com/v2/index.html#/
-
循环变动:C
- 这种周期变动的特征表现为增加和减少交替出现,但是并不具严格规则的周期性连续变动。最典型的周期案例就是市场经济的商业周期和的整个国家的经济周期。
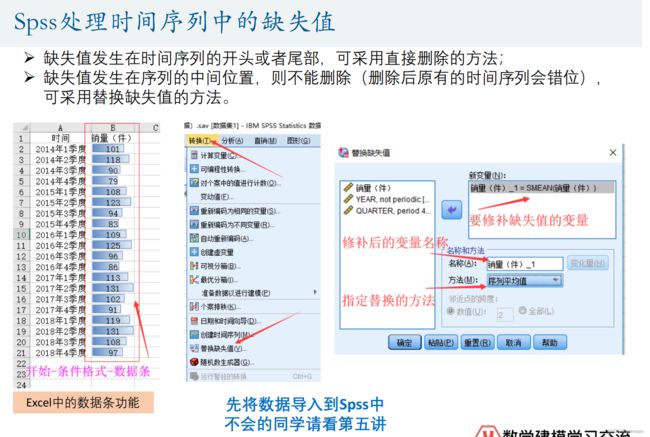
Spss处理时间序列中的缺失值
SPSS中七种指数平滑方法的简单介绍
Simple模型
线性趋势模型(linear trend)
阻尼趋势模型(Damped trend)
简单季节性(Simple seasonal)
温特模型(Winters’ additive)
一元时间序列分析的模型
时间序列的平稳性(stationary series)
差分方程
AR(p )模型(auto regressive)
MA(q)模型(moving average)
MA模型和AR模型的关系
ARMA(p,q)模型
模型选择:AIC和BIC准则(选小原则)
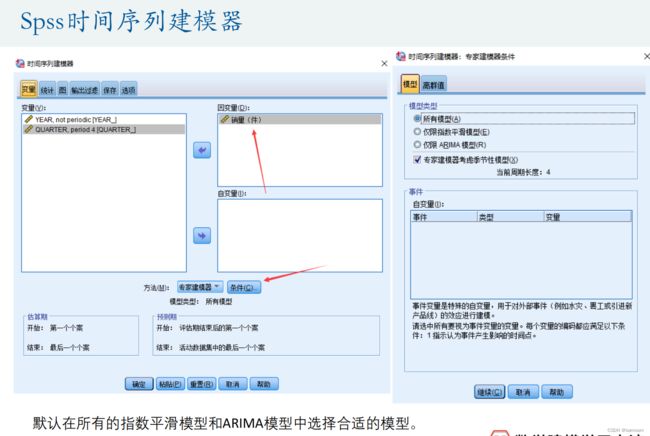
Spss时间序列建模的思路
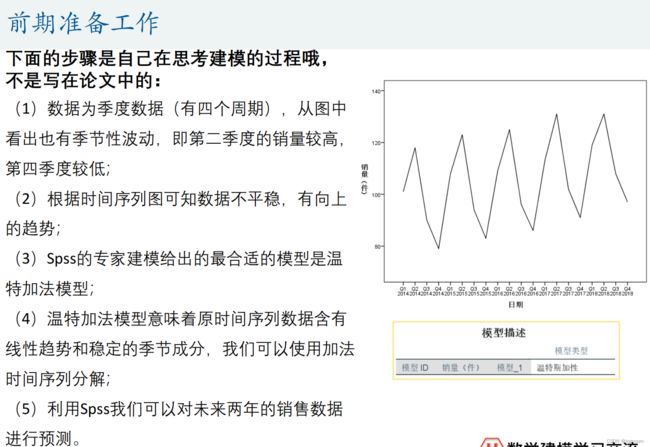
下面的步骤是自己在思考建模的过程哦,不是写在论文中的:
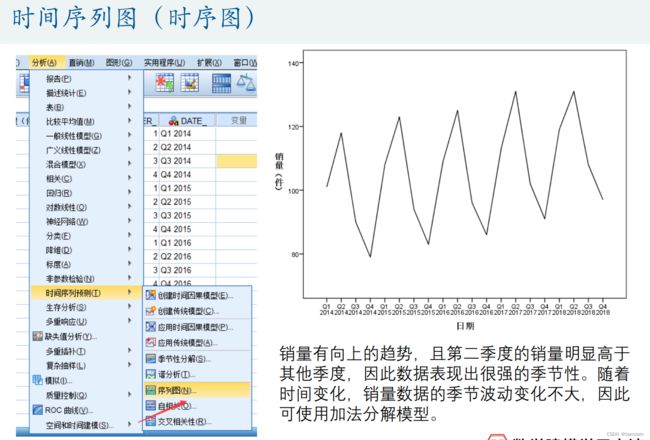
- (1)处理数据的缺失值问题、生成时间变量并画出时间序列图;
- (2)数据是否为季度数据或者月份数据(至少有两个完整的周期,即两年),如果是的话则要观察图形中是否存在季节性波动。
- (3)根据时间序列图大致判断数据是否为平稳序列(数据围绕着均值上下波动,无趋势和季节性)
- (4)打开Spss,分析‐‐时间序列预测—创建传统模型(高版本的Spss可能才有这个功能哦,我用的是24版本,安装包可以在第5讲的课件压缩包里面下载),看看Spss专家建模器得出的最优的模型类型。
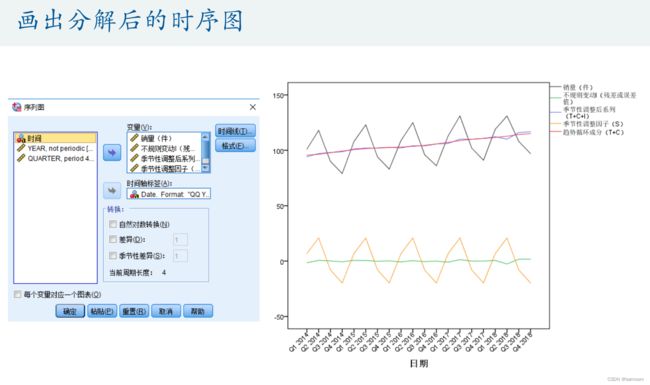
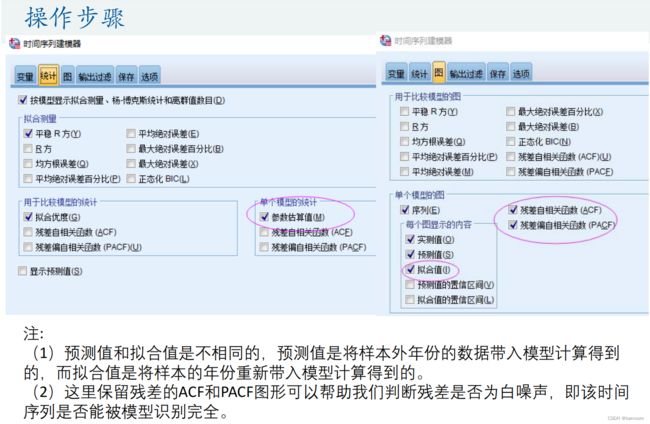
- (5)如果最后的结果是ARIMA(p,0,q)模型,那么我们就可以画出时间序列的样本ACF和PACF图形进行分析;如果得到的是ARIMA(p,1,q)模型,我们可以先对数据进行1阶差分后再用ACF和PACF图形分析;如果得到的结果与季节性相关,那么我们可以考虑使用时间序列分解。
12.预测模型
本讲首先将介绍灰色预测模型,然后将简要介绍神经网络在数据预测中的应用,在本讲的最后,我将谈谈我个人对于数据预测的一些看法。
灰色预测模型
- 白色系统——系统的信息是完全明确的。
- 灰色系统——系统的部分信息已知,部分信息未知。
- 黑色系统——系统的内部信息是未知的。
灰色预测是对既含有已知信息又含有不确定信息的系统进行预测,就是对在一定范围内变化的、与时间有关的灰色过程进行预测。
灰色预测对原始数据进行生成处理来寻找系统变动的规律,并生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。
GM(1,1)模型: Grey(Gray) Model
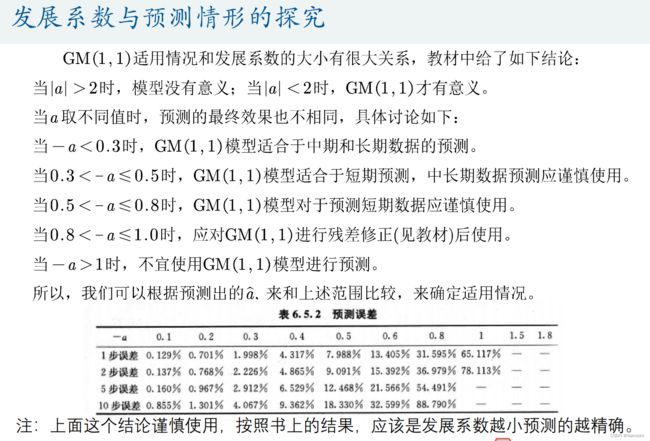
GM(1,1)模型的评价
下面是我自己的看法,使用哪种模型进行预测是仁者见仁智者见智的事情:
(1)数据是以年份度量的非负数据(如果是月份或者季度数据一定要用我们上一讲学过的时间序列模型);
(2)数据能经过准指数规律的检验(除了前两期外,后面至少90%的期数的光滑比要低于0.5);
(3)数据的期数较短且和其他数据之间的关联性不强(小于等于10,也不能太短了,比如只有3期数据),要是数据期数较长,一般用传统的时间序列模型比较合适
灰色预测的例题
预测的题目的一些小套路
(1)看到数据后先画时间序列图并简单的分析下趋势(例如:我们上一讲学过的时间序列分解);
(2)将数据分为训练组和试验组,尝试使用不同的模型对训练组进行建模,并利用试验组的数据判断哪种模型的预测效果最好(比如我们可以使用SSE这个指标来挑选模型,常见的模型有指数平滑、ARIMA、灰色预测、神经网络等)。
(3)选择上一步骤中得到的预测误差最小的那个模型,并利用全部数据来重新建模,并对未来的数据进行预测。
(4)画出预测后的数据和原来数据的时序图,看看预测的未来趋势是否合理
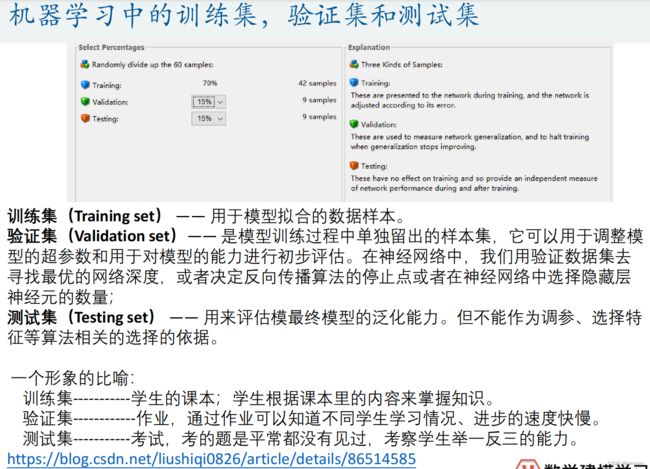
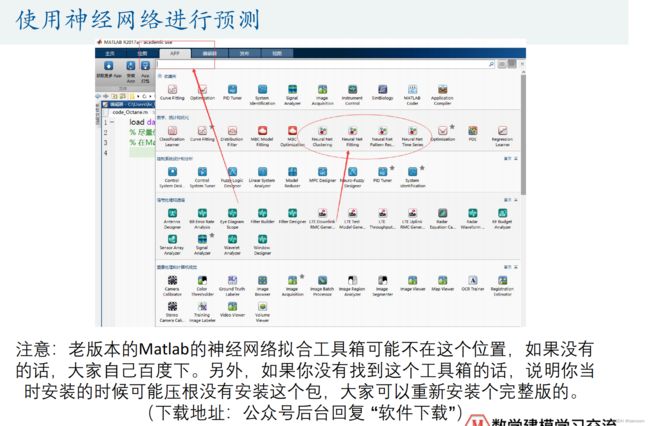
BP神经网络预测
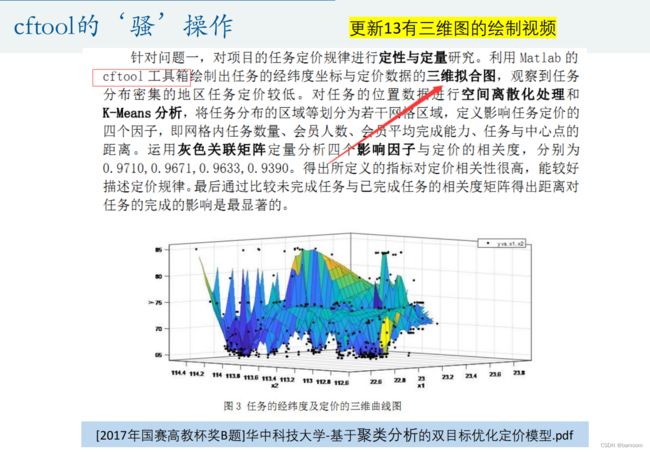
13.SVD和图形处理
奇异值分解(Singular Value Decomposition)是线性代数中一种重要的矩阵分解,其在图形学、统计学、推荐系统、信号处理等领域有重要应用。本讲我们将介绍奇异值分解在图形压缩中的运用,并将简单介绍下Matlab对于图形和视频的处理。
奇异值分解
SVD的评价和应用
14.主成分分析
本讲将介绍主成分分析(Principal Component Analysis,PCA),主成分分析是一种降维算法,它能将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息。一般来说,当研究的问题涉及到多变量且变量之间存在很强的相关性时,我们可考虑使用主成分分析的方法来对数据进行简化。
数据降维
- 降维是将高维度的数据(指标太多)保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的。
- 在实际的生产和应用中,降维在一定的信息损失范围内,可以为我们节省大量的时间和成本。降维也成为应用非常广泛的数据预处理方法。
降维具有如下一些优点:
1.使得数据集更易使用;
2.降低算法的计算开销;
3.去除噪声;
4.使得结果容易理解。