【力扣刷题总结】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 1、找到数组的中间位置
- 2、杨辉三角 II
- 3、三数之和
- 4、验证回文串
- 5、最长公共前缀
- 6、反转字符串中的单词 III
- 7、找出字符串中第一个匹配的下标
- 8、整数反转
- 9、盛最多水的容器
- 10、删除有序数组中的重复项 II
- 11、在排序数组中查找元素的第一个和最后一个位置
- 12、两数之和 II - 输入有序数组
- 13、排列硬币
- 14、找不同
- 15、判断子序列
- 16、字符串中的单词数
- 17、长按键入
- 18、IP 地址无效化
- 19、连续字符
- 20、删除有序数组中的重复项
- 21、有效的括号
- 22、 反转字符串中的单词
- 23、有效的字母异位词
- 24、左旋转字符串
- 25、买卖股票的最佳时机
- 26、一逗到底
- 27、旋转图像
- 28、轮转数组
- 29、最大子数组和
- 29、判断一个数字是否可以表示成三的幂的和
- 30、 打家劫舍
- 总结
前言
从笔者进入大学开始到4月1日,刷了一些算法题,因为后面将会开始学习OC以及备战蓝桥杯,所以特此对之前刷过的力扣题做一个全面的总结。

1、找到数组的中间位置
代码:
int findMiddleIndex(int* nums, int numsSize) {
int total = 0;
for (int i = 0; i < numsSize; ++i) {
total += nums[i];
}
int sum = 0;
for (int i = 0; i < numsSize; ++i) {
if (2 * sum + nums[i] == total) {
return i;
}
sum += nums[i];
}
return -1;
}
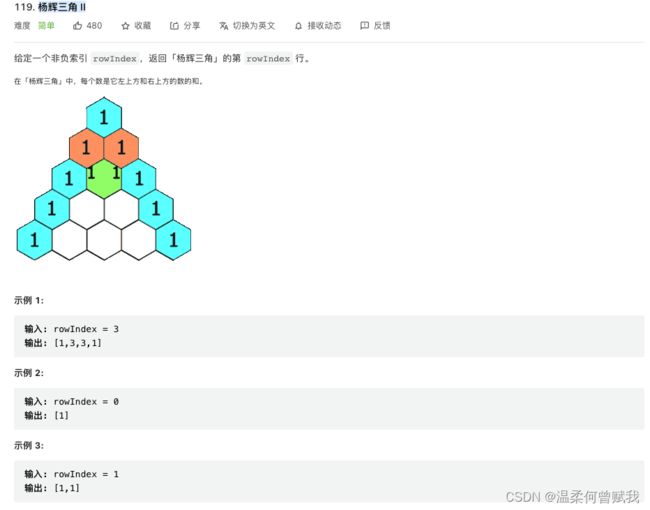
2、杨辉三角 II
思路:
- 首先我们可以明白每一行的第一个与最后一个元素的结果一定是1
- 上一行的第i-1与第i个元素想加就是当前行的第i个元素的值。
- 然后我们构造一个二维数组来存储杨辉三角
代码:
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* getRow(int rowIndex, int* returnSize){
*returnSize = rowIndex + 1;
int * num = malloc(sizeof(int)*(rowIndex+1));
for(int i=0; i<=rowIndex; ++i)
{
for(int j=i; j>=0; j--)
{
if(j==0 || j==i)
{
num[j]=1;
}
else
{
num[j] = num[j]+num[j-1];
}
}
}
return num;
}
3、三数之和
思路: 因为数组在力扣的AC格式十分特殊,所以这道题的AC代码显得格外麻烦,实际上这题并不难,但是我们需要分析的情况特别多
- 首先我们需要对这个乱序数组进行排序,然后判断首元素是否大于0,若大于0则直接返回空数组
- 然后从0开始遍历三个元素中的第一个元素,将第二个元素放在第一个元素的下一个下标位置,然后将第三个元素放到数组末尾,注意此时的判断条件是mid
< right。如果符合条件则进入数组- 然后对mid++,right–。因为第一个元素会变大,那么对于其他两个元素只有这一种符合条件,如果两个都减则不知道不符合条件是该调整哪一个元素
- 因为我们的数组中肯定有相同的元素,所以每录入一种情况我们都需要进行去重
代码:
int cmp(const void *a,const void *b)
{
return *(int*)a - *(int*)b;
}
int** threeSum(int* nums, int numsSize, int* returnSize, int** returnColumnSizes)
{
*returnSize = 0;
if(numsSize < 3)
return NULL;
qsort(nums,numsSize,sizeof(int),cmp);
int **ans = (int **)malloc(sizeof(int *) * numsSize *numsSize);
*returnColumnSizes = (int *)malloc(sizeof(int) * numsSize * numsSize);
int i,j,k,sum;
int indexLeft = 0;
int indexMiddle = 0;
int indexRight = 0;
//快排过后,使用三指针 遍历
//左边遍历到倒数第三位即可
for(indexLeft = 0; indexLeft< numsSize - 2; indexLeft++)
{
if(nums[indexLeft] > 0)
{
//因为是快排的结果,所以如果出现大零的
//后面的值都是大于0的
return ans;
}
//如果值相同 则不需要遍历
if(indexLeft > 0 && nums[indexLeft] == nums[indexLeft-1])
continue;
indexMiddle = indexLeft + 1;
indexRight = numsSize - 1;
//双指遍历 找到所有的可能
while(indexMiddle < indexRight)
{
sum = nums[indexLeft] + nums[indexMiddle] + nums[indexRight];
if(sum == 0)
{
ans[*returnSize] = (int*)malloc(sizeof(int)*3);
(*returnColumnSizes)[*returnSize] = 3;
ans[*returnSize][0] = nums[indexLeft];
ans[*returnSize][1] = nums[indexMiddle];
ans[*returnSize][2] = nums[indexRight];
*returnSize += 1;
//过滤相等的值
while(indexMiddle < indexRight && nums[indexMiddle] == nums[++indexMiddle]);
while(indexMiddle < indexRight && nums[indexRight] == nums[--indexRight]);
}
else if(sum > 0)
{
//左边递减
indexRight--;
}
else
{
//右边递增
indexMiddle++;
}
}
}
return ans;
}
4、验证回文串
思路: 此题用i来维护原字符串,用j来维护新字符串。
代码:
bool isPalindrome(char * s){
int i = 0,j = 0;
while(s[i]){
if(s[i] >= 48 && s[i] <= 57)
{ s[j] = s[i];
j++;
}
else if(s[i] >= 65 && s[i] <= 90){
s[i] += 32;
s[j]= s[i];
j++;
}
else if(s[i] >= 97 && s[i] <= 122)
s[j++] = s[i];
i++;
}
int left = 0,right = j - 1;
while(left < right){
if(s[left] != s[right])
return false;
left++;
right--;
}
return true;
}
5、最长公共前缀
思路: 通过垂直扫描,逐步遍历每一个元素的相同位数的下标,当全都符合时则录入输出的字符串,否则返回字符串
代码:
char* longestCommonPrefix(char** strs, int strsSize) {
if(strsSize == 1) return strs[0];
int minLen = strlen(strs[0]);
for (int i = 1; i < strsSize; ++i) if(minLen > strs[i]) minLen = strlen(strs[i]);
char* arr = (char*)malloc(sizeof(char) * (minLen + 1));
//arr = NULL;
for (int i = 0; i < minLen; ++i) {
char c = strs[0][i];
for (int j = 1; j < strsSize; ++j) {
if(strs[j][i] != c) {
arr[i] = '\0';
return arr;
} else {
arr[i] = c;
}
}
}
arr[minLen] = '\0';
return arr;
}
6、反转字符串中的单词 III
思路:
逐步反转每个单词,但保留空格,这就需要我们每次在开始时确定left与right指针的位置,然后让单词反转,当遍历到空格时直接跳过,因为我们是在原字符串中修改得到结果
char * reverseWords(char * s){
int len = strlen(s);
int i=0;
while(i<len)
{
int start = i;//使用多次双指针需要在开头提前设置一个变量来确定下一次读取开始的位置
while(s[i]!=' ' && i<len)
{
++i;
}
int left = start;
int right = i-1;
while(left<right)
{
char ch = s[left];
s[left] = s[right];
s[right] = ch;
++left;
--right;
}
while(s[i]==' ' && i<len)
{
++i;
}
}
return s;
}
7、找出字符串中第一个匹配的下标
思路: 利用选择排序的思想,用i维护长字符串,j维护短字符串。
代码:
int strStr(char * haystack, char * needle){
int i=0;
int j=0;
int len_1 = strlen(haystack);
int len_2 = strlen(needle);
int count = 0;
int fcount;
for(i=0; i+len_2<=len_1; ++i)
{
bool t = true;
for(j=0; j<len_2; ++j)
{
if(haystack[i+j]!=needle[j])
{
t = false;
break;
}
}
if(t)
{
return i;
}
}
return -1;
}
8、整数反转
思路: 不断得到整数的最后一位,位于第几位就乘几次10,每次更新记得加上其当前位置取模的值
代码:
int reverse(int x){
long t = 0;
while(x!=0)
{
t = t*10 + x%10;
x = x/10;
}
if((int)t != t)
return 0;
return (int)t;
}
9、盛最多水的容器
思路: 这题我们用left维护容器左边,right维护容器右边。每次更新都会用fmax更新能承的体积的最大值。
宽度为right-left。高度是两边所对应的高度的较短的那一边 如果height[left]=height[right],则高度为height[right],若height[right] < height[left],则高度为height[left], 如果右边高就++left,左边高就–right;
代码:
int maxArea(int* height, int heightSize){
int left = 0;
int right = heightSize-1;
int fcount = 0;;
int s = 0;
int h;
bool t;
while(left<right)
{
if(height[left]<=height[right])
{
h = height[left];
t = 1;
}
if(height[right]<height[left])
{
h = height[right];
t = 0;
}
s = h*(right-left);
fcount = fmax(fcount, s);
if(t==1)
++left;
if(t==0)
--right;
}
return fcount;
}
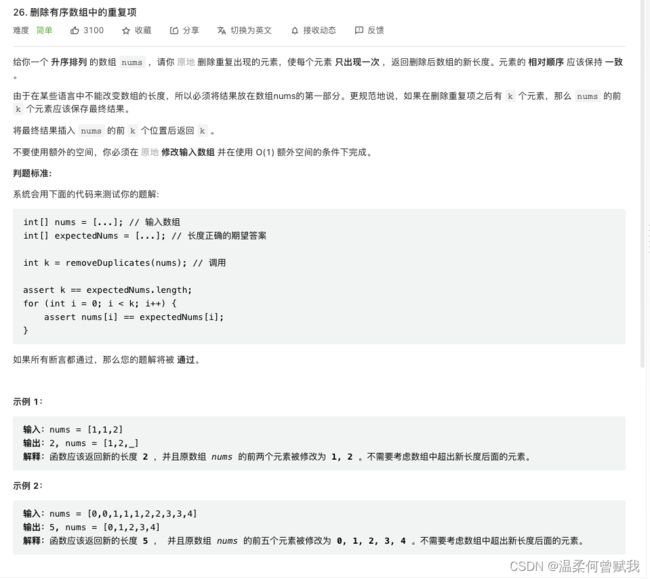
10、删除有序数组中的重复项 II
思路: 同样用left与right维护数组,因为一个元素只能出现两次所以当 nums[right] != nums[left - 2],
nums[left] = nums[right];
代码:
int removeDuplicates(int* nums, int numsSize){
if(numsSize<=2)
return numsSize;
int left = 2;
int right = 2;
while(right<numsSize)
{
if(nums[right] != nums[left - 2])
{
nums[left] = nums[right];
++left;
}
++right;
}
return left;
}
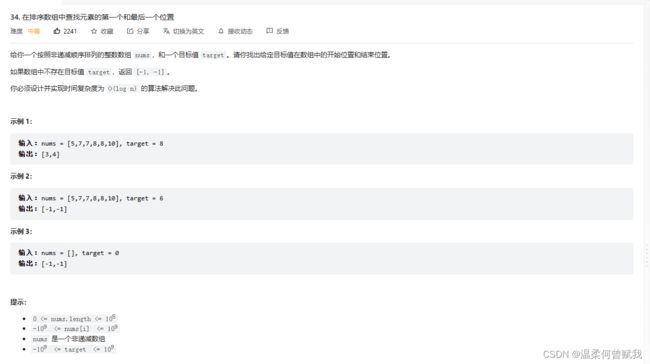
11、在排序数组中查找元素的第一个和最后一个位置
思路; 设立左指针与右指针,从左边遍历查找第一个元素,右边遍历查找第二个元素
代码:
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* searchRange(int* nums, int numsSize, int target, int* returnSize){
int *arr = malloc(sizeof(int)*2);
arr[0] = arr[1] = -1;
int left = 0;
int right = numsSize - 1;
for(left=0; left<=right; ++left)
{
if(target == nums[left])
{
arr[0] = left;
break;
}
}
for( ; right>=left; --right)
{
if(target == nums[right])
{
arr[1] = right;
break;
}
}
*returnSize = 2;
return arr;
}
12、两数之和 II - 输入有序数组
思路: 也是使用左右指针,若左右指针相加大于target则–right,小于则++left
代码:
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* twoSum(int* numbers, int numbersSize, int target, int* returnSize){
int left = 0;
int right = numbersSize - 1;
int *arr;
arr = (int*)malloc(sizeof(int)*2);
*returnSize = 2;
while(left<right)
{
if(target == numbers[left] + numbers[right])
{
arr[0] = left+1;
arr[1] = right+1;
return arr;
}
if(target < numbers[left] + numbers[right])
{
right--;
}
if(target > numbers[left] + numbers[right])
{
left++;
}
}
return arr;
}
13、排列硬币
代码:
int arrangeCoins(int n){
int low = 1, high = n, mid; //初始化
while(low <= high){ //二分查找
mid = low + (high - low) / 2;
if((long)(mid + 1) * mid / 2 > n) //防止溢出
high = mid - 1;
else if((long)(mid + 1) * mid / 2 < n - mid)
low = mid + 1;
else
return mid;
}
return mid;
}
14、找不同
思路: 看到找不同类型的题首先应该想到位运算
代码:
int cmp(const void *a, const void *b)
{
return *(char*)a - *(char*)b;
}
char findTheDifference(char * s, char * t){
int len1 = strlen(s);
int len2 = strlen(t);
char returnchar = 0;
for(int i=0; i<len1; ++i)
{
returnchar ^=s[i];
}
for(int i=0; i<len2; ++i)
{
returnchar^= t[i];
}
return returnchar;
}
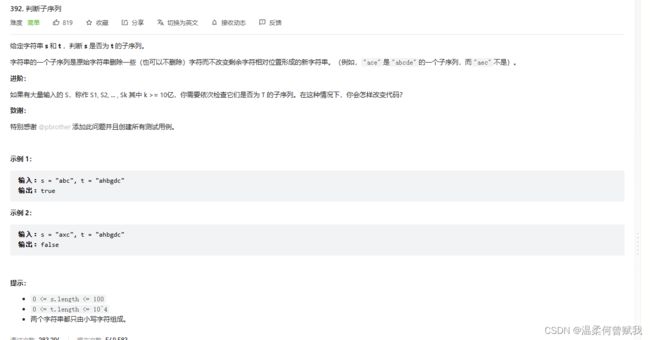
15、判断子序列
思路: 不断遍历,如果有相同字母就++left,如果最后left==数组长度则为真
代码:
bool isSubsequence(char * s, char * t){
int len1 = strlen(s);
int len2 = strlen(t);
int right = 0;
int left = 0;
while(right<len2 &&left<len1)
{
if(s[left] == t[right])
{
++left;
}
++right;
}
return left == len1;
}
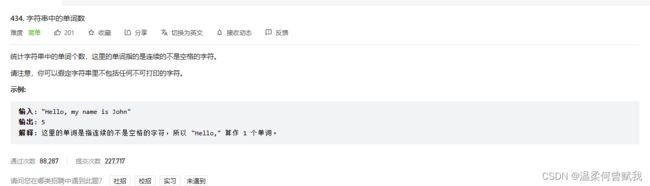
16、字符串中的单词数
思路: 当为0以及当当前下标对应的不为空,前一个下标对应的为空,则cnt++
代码:
int countSegments(char * s)
{
int cnt = 0;
int len = strlen(s);
for(int i=0; i<len; ++i)
{
if((i==0|| s[i-1]==' ')&& s[i]!=' ')
cnt++;
}
return cnt;
}
17、长按键入
思路: 用name字符串来匹配typed字符串若匹配成功则移动到下一个字符,若当前两字符串字符不相等则返回false
代码:
bool isLongPressedName(char* name, char* typed) {
int n = strlen(name), m = strlen(typed);
int i = 0, j = 0;
while (j < m) {
if (i < n && name[i] == typed[j]) {
i++;
j++;
} else if (j > 0 && typed[j] == typed[j - 1]) {
j++;
} else {
return false;
}
}
return i == n;
}
18、IP 地址无效化
思路:创造一个新字符串来存储修改后的字符串
思路:
char * defangIPaddr(char * address){
int length=strlen(address);
char* str = (char*)malloc(length + 6 + 1);
int j=0;
for(int i=0;i<length;i++){
if(address[i]=='.'){
str[j]='[';
str[j+1]='.';
str[j+2]=']';
j=j+3;
}
else{
str[j]=address[i];
j++;
}
}
str[j]='\0';
return str;
}
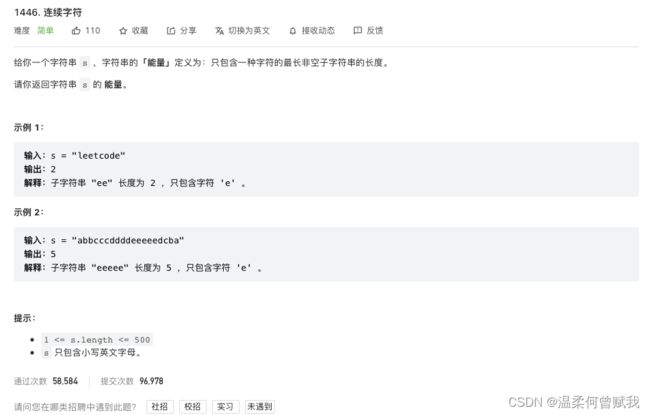
19、连续字符
思路: 设立两个指针,然后不断更新最大值
代码:
int maxPower(char * s){
int len = strlen(s);
int left = 0;
int right = 0;
int i=1;
int fm = 0;
int f=1;
while(right<len)
{
while(s[left]==s[right])
{
++right;
}
f = right-left;
left = right;
fm = fmax(f, fm);
}
return fm;
}
20、删除有序数组中的重复项
思路: 此题的关键是保证没有出现两个相同的元素
int removeDuplicates(int* nums, int numsSize){
if(numsSize == 0)
return 0;
int left = 1;
int right = 1;
while(right<numsSize)
{
if(nums[right] != nums[right-1])//保证没有出现两个相同的元素
{
nums[left] = nums[right];
++left;
}
++right;
}
return left;
}
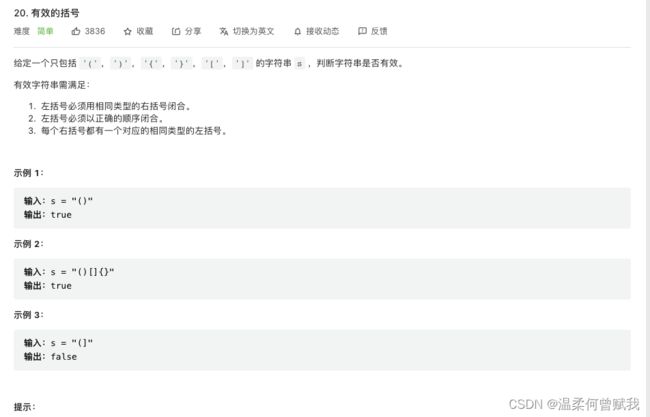
21、有效的括号
思路: 以两个为一对一一匹配。如果匹配则继续遍历,匹配不成功就返回false。
代码:
char pair(char a)
{
if(a == '(')
{
return ')';
}
if(a == '{')
{
return '}';
}
if(a == '[')
{
return ']';
}
return 0;
}
bool isValid(char * s){
int len = strlen(s);
if(len % 2 == 1)
{
return false;//有效括号匹配一定是偶数,不可能是奇数
}
char ch;
int stack[len+1];
int top = 0;
for(int i=0; i<len; i++)
{
char ch = pair(s[i]);
if(ch)
{
stack[top++] = ch;
}
else
{
if(top == 0 || stack[top-1] != s[i])
{
return false;
}
top--;
}
}
return top==0;
}
22、 反转字符串中的单词
思路:
移除多余空格 将整个字符串反转 将每个单词反转
代码:
void fanzhuan(char* s,int left, int right)
{
int temp;
while(left<right)
{
temp = s[left];
s[left] = s[right];
s[right] = temp;
++left;
--right;
}
}
char * reverseWords(char * s){
int left = 0;
int right = 0;
int len1 = strlen(s);
while(right<len1)
{
if(left==0&&s[right] == ' ' || (left!=0&&s[left-1]==' '&&s[right]==' '))
{
right++;
}
else
{
s[left++] = s[right++];
}
}
if(s[left-1] == ' ')
{
s[left-1] = '\0';
}
else
{
s[left] = '\0';
}
int len2 = strlen(s);
fanzhuan(s, 0, len2-1);
int left1 = 0;
int right1 = 0;
int i=0;
while(i<len2)
{
left1 = i;
while(s[i]!=' ' && i<len2)
{
i++;
}
right1 = i-1;
fanzhuan(s, left1, right1);
i++;
}
return s;
}
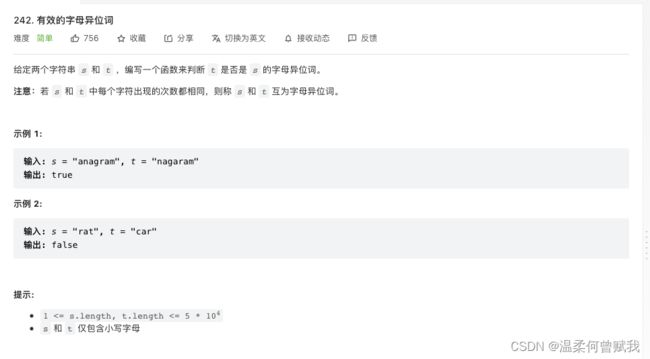
23、有效的字母异位词
思路:利用哈希表存储字母,有对应的字母对于s字符串就加1,t就-1。
代码:
bool isAnagram(char * s, char * t){
int len_s = strlen(s), len_t = strlen(t);
if (len_s != len_t) {
return false;
}
int a[26] = {0};
for(int i=0; i<len_s; i++)
{
a[s[i]-'a']++;
}
for(int i=0; i<len_t; i++)
{
a[t[i] - 'a']--;
}
for(int i = 0; i<26; i++)
{
if(a[i] < 0) {
return false;
}
}
return true;
}
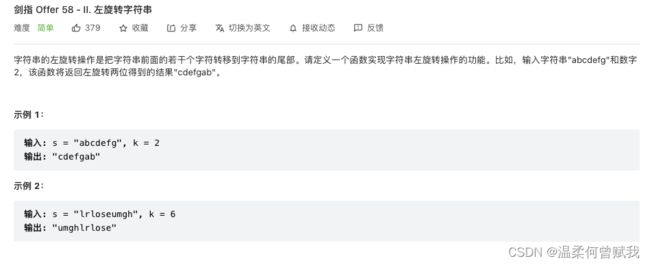
24、左旋转字符串
思路: 反转部分字符串然后整体反转
代码:
char* reverse(char* s, int left, int right) {
while(left < right) {
char temp = s[left];
s[left] = s[right];
s[right] = temp;
left++;
right--;
}
return s;
}
char* reverseLeftWords(char* s, int n) {
int len = strlen(s);
s = reverse(s, 0, n-1);
s = reverse(s, n, len-1);
s = reverse(s, 0, len-1);
return s;
}
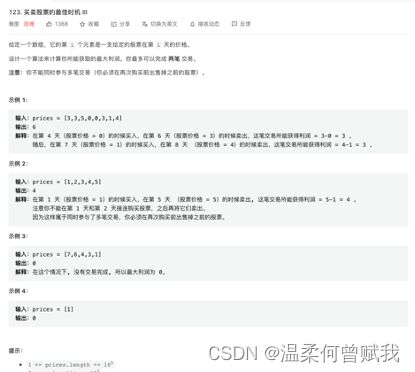
25、买卖股票的最佳时机
思路:
- 首先我们可以从买卖股票12中得知,我们解决此题需要弄清我们买卖股票时会有几个状态,对于买卖股票1,我们因为只进行一次买卖,所以我们只需要有两种状态:当前手上有股票与当前手上没有股票的状态。
- 为什么我们需要用这两种状态呢,因为这两种状态恰好可以包括我们在买卖股票时所有状态。我们要着重理解这两种状态。当前手上有股票的状态并不代表着股票就是今天买的,很有可能股票时前几天买的,我们只需要将购买今天股票后手上所剩的钱与昨天已经买股票后所剩下的现金进行对比取最大值。同样的,当前手上没股票的状态也不意味着一定没有买股票,可能是今天刚好把股票卖出去了,
- 那么我们现在来看这道题,因为我们可以买卖两次,所以我们需要用四种状态来表示。分别是第一次买卖时持有与不持有股票,第二次买卖时持有与不持有股票。
- 另外我们在学习动态规划时我们要搞清楚我们的做题步骤。 做题步骤分为五部分
- 确定dp数组以及下标含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推倒dp数组; 其中我觉得第一与第二步是动态规划中比较重要的一步。我们做题也最好按照这个步骤来做。
代码:
int maxProfit(int* prices, int pricesSize){
int dp[pricesSize][5];
dp[0][1] = 0;//这是第一次不持有股票的状态
dp[0][2] = -prices[0];//这是第一次持有股票的状态
dp[0][3] = 0;//第二次不持有
dp[0][4] = -prices[0];//第二次之后持有
for(int i=1; i<pricesSize; i++){
dp[i][1] = fmax(dp[i-1][1], dp[i-1][2]+prices[i]);//对前一天的对比与前一天持有时今天卖出的对比。
dp[i][2] = fmax(dp[i-1][2], 0-prices[i]);//第一次持有股票后手上的钱的对比就是对昨天持有与当天买股票后手上所剩下的钱的对比
dp[i][3] = fmax(dp[i-1][3], dp[i-1][4]+prices[i]);// 第二次对前一天的对比与前一天持有时今天卖出的对比。
dp[i][4] = fmax(dp[i-1][4], dp[i-1][1]-prices[i]);// 第一次持有股票后手上的钱的对比就是对昨天持有与当天买股票后手上所剩下的钱的对比
}
return dp[pricesSize-1][3];//返回最终手上所剩下的钱
}
26、一逗到底
思路: 首先我们要明白我们题意是删除两个及两个以上的逗号,如果只有一个则将其保存。
- 我们先创建一个新的字符串来存储我们修改后的字符串
- 我们要搞清楚我们正常替换时需要的判断的条件,即当前下标所对应的元素不是逗号或者是逗号但是下一个不是逗号。
- 否则就进入另一种情况,即当前与下一个元素下标所对应的都是逗号,那么就先将一个逗号存进新字符串,然后不断用i维护旧字符串直至当前元素不为逗号
代码:
#include 27、旋转图像
思路 : 模拟一个数组,先将原数组存进模拟数组,然后旋转后的数组的最后一列就是原数组的第一行,倒数第二列就是原数组第二行。
注意在这里我们需要用模拟后的数组对原数组的值进行修改,然后返回原数组
代码:
void rotate(int** matrix, int matrixSize, int* matrixColSize) {
int Newmarix[matrixSize][matrixSize];
for (int i = 0; i < matrixSize; i++) {
for (int j = 0; j < matrixSize; j++) {
Newmarix[i][j] = matrix[i][j];
}
}
for (int i = 0; i < matrixSize; i++) {
for (int j = 0; j < matrixSize; j++) {
matrix[i][j] = Newmarix[j][matrixSize - i - 1];
}
}
28、轮转数组
思路1: 看到这题很容易想到之前做的一道链表题—旋转链表,都是将元素与向右移动k个位置。
- 我们首先用一个新数组来存储移动后的数组的值,这就需要我们将新数组的每个值的位置对应每个移动数组的正确位置。
- 然后我们就开始思考怎样得到新数组。我的思想将原数组的第一个下标元素与新数组的同样的元素的下标对应,例如移动2个位置,那么新数组的[2]就对应着原数组的第一个元素,这样我们就可以联想到Newnum[(k+i]
% numssize] = nums[i];- 然后我们将新数组的值赋给原数组然后返回原数组
代码:
void rotate(int* nums, int numsSize, int k){
int Newnums[numsSize];
for (int i = 0; i < numsSize; i++) {
Newnums[(k + i) % numsSize] = nums[i];
}
for (int i = 0; i < numsSize; i++) {
nums[i] = Newnums[i];
}
}
思路2 :
思路2就是要看了题解才能想到的方法。先将整个数组反转,然后反转下标为0-k-1的元素,再反转k - numssize – 1的元素
代码:
void swap(int* a, int* b) {
int t = *a;
*a = *b;
*b = t;
}
void lunhuan(int* nums, int left, int right) {
while (left < right) {
swap(&nums[left], &nums[right]);
left++;
right--;
}
}
void rotate(int* nums, int numsSize, int k) {
k%=numsSize;
lunhuan(nums, 0, numsSize-1);
lunhuan(nums, 0, k-1);
lunhuan(nums, k, numsSize-1);
return nums;
}
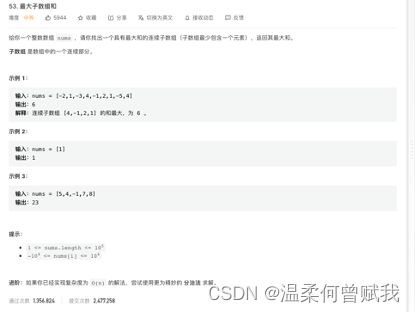
29、最大子数组和
思路: 首先按照我们的动态规划五部曲可以知道我们首先需要确定dp数组及其下标的含义。
这道题的dp数组的含义是以第i个元素结尾的字数组的最大值。 dp[i] = fmax(pre, dp[i] + pre);
首先我们可以知道我们的dp[i]一定是以第i个元素结尾的,要么就是将第i-1结尾的dp加上第i个元素作为dp[i],
要么就是以第i个元素作为dp[I], 无论是这两种情况中的哪一种,我们都能得到连续的子数组。 然后不断更新maxsum来得到最大子数组和
代码:
int maxSubArray(int* nums, int numsSize) {
int maxsum = nums[0];
int pre = 0;
for (int i = 0; i < numsSize; ++i) {
pre = fmax(pre + nums[i], nums[i]);
maxsum = fmax(pre, maxsum);
}
return maxsum;
}
29、判断一个数字是否可以表示成三的幂的和
思路: 将十进制转换为三进制。如果三进制有任意一位为2,则返回flase。
另外这里我的方法是将三进制用数组的方式来存储,当然也可以直接判断每次取模是否有2。对一个数取模得到的其实就是某一位对应进制的数。
代码:
bool checkPowersOfThree(int n){
int len = 0;
int num[1000] = {0};
while (n) {
num[len++] = n%3;
n /= 3;
}
for (int i = 0; i < len; i++) {
if (num[i] == 2) {
return false;
}
}
return true;
}
//将整数转换为二进制来做
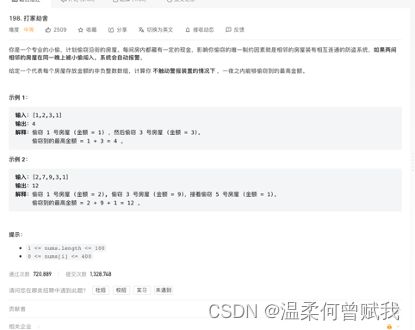
30、 打家劫舍
思路: 首先此题是一道很经典的动态规划题目
在这里我们需要明白题意,我们既可以偷隔着一间房子的两家,也可以偷隔着两间房子的两家,主要是需要保证我们能偷到最多的钱在这里我们的dp数组的含义便是在下标为i处时我们所能得到的最大金额。 dp[i] = fmax(dp[i - 2] + nums[i],
dp[i - 1]); 在这里我们需要明白为什么这样设置我们的递推公式。因为我们下标为i-1时我们没有办法偷i,
下标为i-2时我们就一定要偷来保证我们能得到最大的钱 然后我们初始化dp数组。
因为dp数组的含义是在第i间房屋时我们能得到的最大钱,所以dp[0] = nums[0]; dp[1] = fmax(nums[0],
nums[1]); 最后我们返回return dp[numsSize - 1];,就是在第i间房屋时的最大值
代码:
int rob(int* nums, int numsSize){
if (numsSize == 1) {
return *nums;
}
int maxsum = 0;
int dp[numsSize];
dp[0] = nums[0];
dp[1] = fmax(nums[0], nums[1]);
for (int i = 2; I < numsSize; i++) {
dp[i] = fmax(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[numsSize - 1];
}
总结
总结了一部分力扣题,但还没总结完,后面会加以补充、