力扣刷题笔记
206.反转链表
题目
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
思路
双指针
首先定义一个cur指针,指向头结点,再定义一个pre指针,初始化为null。
然后就要开始反转了,首先要把 cur->next 节点用tmp指针保存一下,也就是保存一下这个节点。
为什么要保存一下这个节点呢,因为接下来要改变 cur.next 的指向了,将cur.next 指向pre ,此时已经反转了第一个节点了。
接下来,就是循环走如下代码逻辑了,继续移动pre和cur指针。
最后,cur 指针已经指向了null,循环结束,链表也反转完毕了。 此时我们return pre指针就可以了,pre指针就指向了新的头结点。
注意,需要定义临时节点temp指向cur的下一个。
代码如下:
class Solution {
public ListNode reverseList(ListNode head) {
ListNode cur=head;
ListNode pre=null;
ListNode temp;
while(cur!=null){
temp=cur.next;
cur.next=pre;
pre=cur;
cur=temp;
}
return pre;
}
}
递归
递归三部曲
1.确定函数的返回类型及参数:ListNode reverse(ListNode cur,ListNode pre);
2.确定递归的终止条件:如果cur为空,则返回pre
3.确定递归体:记录下一节点;cur指向pre;递归,注意这里调用递归函数中的参数应该为(temp,cur)。理由是下一次调用应该将cur和pre向后移,而cur向后移是temp,pre向后移是cur。
代码如下:
class Solution {
public ListNode reverseList(ListNode head) {
return reverse(head,null);
}
public ListNode reverse(ListNode cur,ListNode pre){
if(cur==null) return pre;
ListNode temp=cur.next;
cur.next=pre;
return reverse(temp,cur);
}
}
24.两两交换链表中的节点
题目
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
思路
建议使用虚拟头结点,这样会方便很多,要不然每次针对头结点(没有前一个指针指向头结点),还要单独处理。
初始时,cur指向虚拟头结点,然后进行如下三步:

操作之后,链表如下:
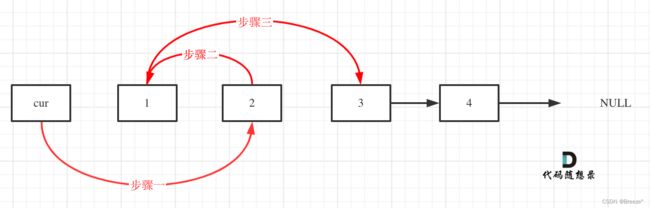
看这个可能就更直观一些了:
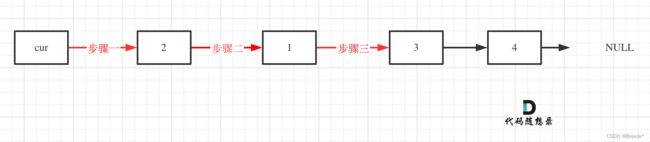
代码如下:
class Solution {
public ListNode swapPairs(ListNode head) {
ListNode dummy=new ListNode(0);
dummy.next=head;
ListNode cur=dummy;
ListNode temp1;
ListNode temp2;
while(cur.next!=null&&cur.next.next!=null){
temp1=cur.next;
temp2=temp1.next.next;
cur.next=cur.next.next;
temp1.next=temp2;
cur.next.next=temp1;
cur=temp1;
}
return dummy.next;
}
}
404.左叶子之和
题目
给定二叉树的根节点 root ,返回所有左叶子之和。
自己思路
前序遍历 构造方法传入节点、result、和类别。
终止条件:如果节点空,返回result;如果为叶子节点,则判断类别。若为左叶子节点,则返回result+val;否则返回result。
迭代体:传入左节点,result,1;传入右节点,result,2;
注意:经过尝试发现如果只有一个根节点,那么不算左叶子节点。
代码如下(通过,执行时间0ms,超过100%,内存消耗39.2mb,超过78.72%):
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
int result=0;
result=sumLeftChild(root,result,2);
return result;
}
public int sumLeftChild(TreeNode root,int result,int flag){
if(root==null) return result;
if(root.left==null&&root.right==null){
if(flag==1) return result+root.val;
else return result;
}else{
result=sumLeftChild(root.left,result,1);
result=sumLeftChild(root.right,result,2);
}
return result;
}
}
代码随想录笔记
左叶子节点明确定义:节点A的左孩子不为空,且左孩子的左右孩子都为空(说明是叶子节点),那么A节点的左孩子为左叶子节点。
判断当前节点是不是左叶子是无法判断的,必须要通过节点的父节点来判断其左孩子是不是左叶子。
如果该节点的左节点不为空,该节点的左节点的左节点为空,该节点的左节点的右节点为空,则找到了一个左叶子
递归
递归的遍历顺序为后序遍历(左右中),是因为要通过递归函数的返回值来累加求取左叶子数值之和。
1.确定函数的参数和返回值
判断一个树的左叶子节点之和,那么一定要传入树的根节点,递归函数的返回值为数值之和,所以为int使用题目中给出的函数就可以了。
2.确定终止条件
如果遍历到空节点,那么左叶子值一定是0
if (root == NULL) return 0;
如果当前遍历的节点是叶子节点,那其左叶子也必定是0
if (root == NULL) return 0;
if (root.left == NULL && root.right== NULL) return 0; //其实这个也可以不写,如果不写不影响结果,但就会让递归多进行了一层。
3.确定单层递归的逻辑
当遇到左叶子节点的时候,记录数值,然后通过递归求取左子树左叶子之和,和 右子树左叶子之和,相加便是整个树的左叶子之和。
int leftValue = sumOfLeftLeaves(root.left); // 左
if (root.left && !root.left.left && !root.left.right) {
leftValue = root.left.val;
}
int rightValue = sumOfLeftLeaves(root.right); // 右
int sum = leftValue + rightValue; // 中
return sum;
总体代码为
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
if (root == null) return 0;
int leftValue = sumOfLeftLeaves(root.left); // 左
int rightValue = sumOfLeftLeaves(root.right); // 右
int midValue = 0;
if (root.left != null && root.left.left == null && root.left.right == null) {
midValue = root.left.val;
}
int sum = midValue + leftValue + rightValue; // 中
return sum;
}
}
总结
首先,左叶子节点的准确定义不明确,因此自己做时按照自己的理解,现在看来有些取巧。
其次,每次写递归都用不上题目给的方法,总想自己新构造方法按自己的逻辑来设置参数。
《代码随想录》的方法可以这样理解:对于当前root节点,leftValue已经算好左子树中的左叶子节点之和;rightValue已经算好右子树中的左叶子节点之和。那么只要相加即可。而如何判断一个左叶子节点就是后面的写法了。
513.找树左下角的值
题目
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
自己思路
思路一:前面做过二叉树的右视图,这里考虑二叉树的左视图得到的list取最后一个就行了。
我的评价是毫无问题啊,代码如下(执行结果:
通过,执行用时:2 ms超过15.96%;内存消耗42.8 MB超过7.92%):
class Solution {
public int findBottomLeftValue(TreeNode root) {
List<Integer> result=new ArrayList<>();
if(root==null) return 0;
Deque<TreeNode> deque=new LinkedList<>();
deque.addFirst(root);
while(!deque.isEmpty()){
int size=deque.size();
Deque<Integer> temp=new LinkedList<>();
for(;size!=0;size--){
TreeNode node=deque.removeLast();
temp.addFirst(node.val);
if(node.left!=null){
deque.addFirst(node.left);
}
if(node.right!=null){
deque.addFirst(node.right);
}
}
result.add(temp.removeLast());
}
return result.get(result.size()-1);
}
}
思路二:上述显然取巧了,而且不好。事实上可以对上述方法进行改进。即层序遍历,但是只保存最后一层的第一个元素即可,可以设置一个变量res,每次迭代只保存每层的第一个元素。
代码如下:
class Solution {
public int findBottomLeftValue(TreeNode root) {
Deque<TreeNode> deque=new LinkedList<>();
int res=0;
deque.addFirst(root);
while(!deque.isEmpty()){
int size=deque.size();
for(int i=0;i<size;i++){
TreeNode node=deque.removeLast();
if(i==0) res=node.val;
if(node.left!=null) deque.addFirst(node.left);
if(node.right!=null) deque.addFirst(node.right);
}
}
return res;
}
}
代码随想录笔记
代码随想录中迭代法即上述思路二。下面主要学习递归法,本题递归法比较难。
112路经总和
题目
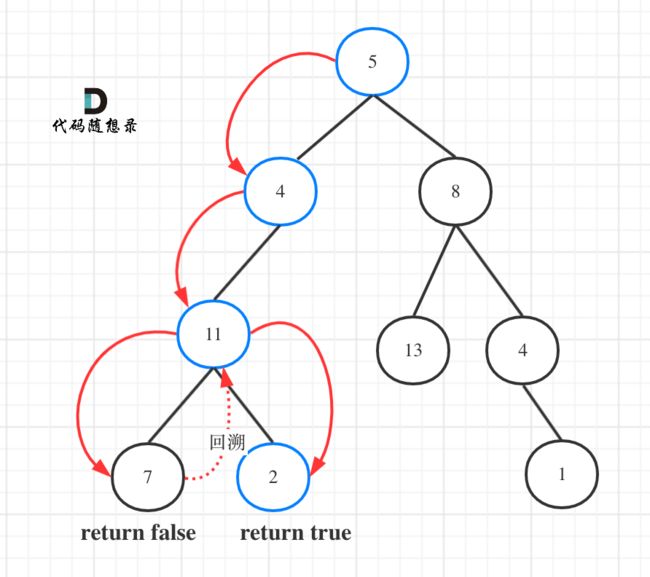
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
自己思路
这题首先想到257题的二叉树所有路径,所以按照那个方法把所有路径都放到map里再比较就好了。
代码如下:
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if(root==null) return false;
Map<Integer,Integer> map=new HashMap<>();
List<Integer> paths=new ArrayList<>();
traversal(root,paths,map);
if(map.containsKey(targetSum)) return true;
else return false;
}
private void traversal(TreeNode root,List<Integer> paths,Map<Integer,Integer> map){
paths.add(root.val);
if(root.left==null&&root.right==null){
int sum = paths.stream().reduce(Integer::sum).orElse(0);
map.put(sum,0);
}
//递归和回溯是同时进行,所以要放在同一个花括号里
if(root.left!=null){
traversal(root.left,paths,map);
paths.remove(paths.size()-1);
}
if (root.right != null) { // 右
traversal(root.right,paths,map);
paths.remove(paths.size() - 1);// 回溯
}
}
}
代码随想录笔记
递归:
1.确定返回值类型
如果要搜索其中一条符合条件的路径,那么递归一定需要返回值,因为遇到符合条件的路径了就要及时返回。
2.确定终止条件
让计数器count初始为目标值,每次减去节点数值,如果最后count==0,那么返回true。
3.确定单层递归的逻辑
代码如下:
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if(root==null) return false;
return traversal(root, targetSum-root.val);
}
public boolean traversal(TreeNode root, int count){
//叶子节点且count为0
if(root.left==null&&root.right==null&&count==0) return true;
//否则遇到叶子节点但count不为0
if(root.left==null&&root.right==null) return false;
if(root.left!=null){
count-=root.left.val;
if(traversal(root.left,count)) return true;
count+=root.left.val;//回溯
}
if(root.right!=null){
count-=root.right.val;
if(traversal(root.right,count)) return true;
count+=root.right.val;//回溯
}
return false;
}
}
113. 路径总和 II
题目
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
思路
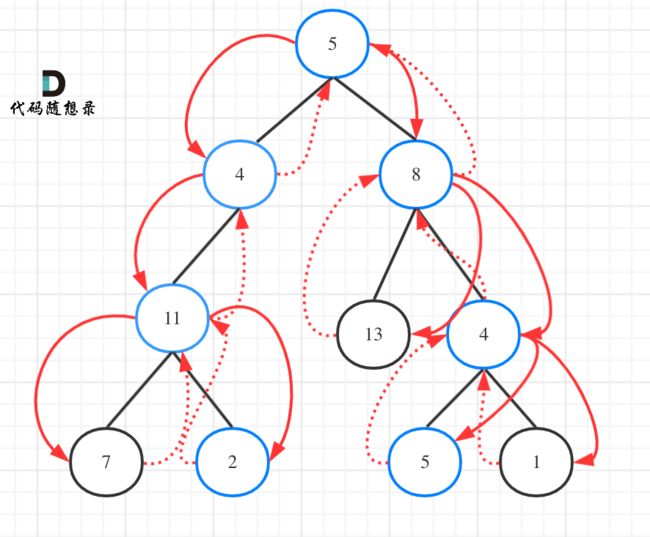
要遍历整个树,找到所有路径,所以递归函数不要返回值!
代码如下
class Solution {
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> result=new ArrayList<>();
if(root==null) return result;
List<Integer> paths=new LinkedList<>();
findpath(root,targetSum-root.val,paths,result);
return result;
}
public void findpath(TreeNode root,int targetSum,List<Integer> paths,List<List<Integer>> result){
paths.add(root.val);
//叶子节点且满足
if(root.left==null&&root.right==null&&targetSum==0){
result.add(new ArrayList<>(paths));
return;
}
//叶子节点但不满足
if(root.left==null&&root.right==null){
return;
}
if(root.left!=null){
targetSum-=root.left.val;
findpath(root.left,targetSum,paths,result);
targetSum+=root.left.val;
paths.remove(paths.size()-1);
}
if(root.right!=null){
targetSum-=root.right.val;
findpath(root.right,targetSum,paths,result);
targetSum+=root.right.val;
paths.remove(paths.size()-1);
}
return;
}
}
106.从中序与后序遍历序列构造二叉树
题目
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
思路
以 后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来再切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。

第一步:如果数组大小为零的话,说明是空节点了。
第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
第五步:切割后序数组,切成后序左数组和后序右数组
第六步:递归处理左区间和右区间
写起来不叫复杂,慢慢按步骤来,代码如下(比较菜,运行时间11ms,你就说通没通过吧):
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
//中序遍历 左中右
//后序遍历 左右中
//前序遍历 中左右
//后序遍历的最后一个为根节点
if(inorder.length==0||postorder.length==0) return null;
int rootValue=postorder[postorder.length-1];//后序遍历的最后一个节点
TreeNode root=new TreeNode(rootValue);
//如果叶子节点
if(postorder.length==1) return root;
int index;
for(index=0;index<inorder.length-1;index++){
if(inorder[index]==rootValue) break;
}
//分割中序遍历数组
int[] left_inorder=new int[index];
int[] right_inorder=new int[inorder.length-index-1];
for(int i=0;i<left_inorder.length;i++) left_inorder[i]=inorder[i];
for(int i=0;i<right_inorder.length;i++) right_inorder[i]=inorder[i+index+1];
//然后如何分割后序遍历数组,显然分割的后序遍历数组的左右数组大小与分割的中序遍历数组相同
int[] left_postorder=new int[index];
int[] right_postorder=new int[inorder.length-index-1];
for(int i=0;i<left_postorder.length;i++) left_postorder[i]=postorder[i];
for(int i=0;i<right_postorder.length;i++) right_postorder[i]=postorder[i+left_postorder.length];
root.left=buildTree(left_inorder,left_postorder);
root.right=buildTree(right_inorder,right_postorder);
return root;
}
}
105.从前序与中序遍历序列构造二叉树
题目
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
思路
与106题思路一致,通过前序遍历确定根节点,然后在中序遍历中划分左右树,再由中序遍历左右树划分前序遍历的数组,进行迭代。
步骤如下:
第一步 如果前序遍历数组大小为零,则根节点为空;
第二步 找到前序遍历数组的第一个作为节点;
第三步 找到节点元素在中序遍历中的位置;
第四步 切分中序遍历数组;
第五步 切分前序遍历数组;
第六步 迭代左右数组;
代码如下:
class Solution {
Map<Integer,Integer> map;
public TreeNode buildTree(int[] preorder, int[] inorder) {
map=new HashMap<>();
for(int i=0;i<inorder.length;i++){
map.put(inorder[i],i);
}
return generateTree(inorder,0,inorder.length,preorder,0,preorder.length);
}
public TreeNode generateTree(int[] inorder,int inBegin,int inEnd,int[] preorder,int preBegin,int preEnd){
if(inBegin>=inEnd||preBegin>=preEnd) return null;
int rootValue=map.get(preorder[preBegin]);
TreeNode node=new TreeNode(inorder[rootValue]);
int lenofleft=rootValue-inBegin;
node.left=generateTree(inorder,inBegin,rootValue,preorder,preBegin+1,preBegin+lenofleft+1);
node.right=generateTree(inorder,rootValue+1,inEnd,preorder,preBegin+lenofleft+1,preEnd);
return node;
}
}
654.最大二叉树
题目
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
创建一个根节点,其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
思路
第一步,如果数组大小为0,则返回空;
第二步,选取nums中最大值,maxIndex;
第三步,以最大值maxIndex为界划分为左右数组;
第四步,创建节点,nums[maxIndex];
第五步,递归执行左数组;
第六步,递归执行右数组;
第七步,返回节点;
代码如下:
class Solution {
public TreeNode constructMaximumBinaryTree(int[] nums) {
if(nums.length==0) return null;
int maxIndex=0;
for(int i=0;i<nums.length;i++){
if(nums[i]>=nums[maxIndex]){
maxIndex=i;
}
}
TreeNode root=new TreeNode(nums[maxIndex]);
int lenofright=nums.length-maxIndex-1;
int[] leftnum=new int[maxIndex];
int[] rightnum=new int[lenofright];
for(int i=0;i<nums.length;i++){
if(i<maxIndex) leftnum[i]=nums[i];
if(i>maxIndex) rightnum[i-maxIndex-1]=nums[i];
}
root.left=constructMaximumBinaryTree(leftnum);
root.right=constructMaximumBinaryTree(rightnum);
return root;
}
}
代码随想录笔记
构造树一般采用的是前序遍历,因为先构造中间节点,然后递归构造左子树和右子树。
递归三部曲:
1.确定递归函数的参数和返回值
参数传入的是存放元素的数组,返回该数组构造的二叉树的头结点,返回类型是指向节点的指针。
2.确定终止条件
题目中说了输入的数组大小一定是大于等于1的,所以我们不用考虑小于1的情况,那么当递归遍历的时候,如果传入的数组大小为1,说明遍历到了叶子节点了。
3.确定单层递归逻辑
先要找到数组中最大的值和对应的下标, 最大的值构造根节点,下标用来下一步分割数组;
最大值所在的下标左区间 构造左子树;
最大值所在的下标右区间 构造右子树;
代码如下:
class Solution {
public TreeNode constructMaximumBinaryTree(int[] nums) {
return constructMaximumBinaryTree1(nums, 0, nums.length);
}
public TreeNode constructMaximumBinaryTree1(int[] nums, int leftIndex, int rightIndex) {
if (rightIndex - leftIndex < 1) {// 没有元素了
return null;
}
if (rightIndex - leftIndex == 1) {// 只有一个元素
return new TreeNode(nums[leftIndex]);
}
int maxIndex = leftIndex;// 最大值所在位置
int maxVal = nums[maxIndex];// 最大值
for (int i = leftIndex + 1; i < rightIndex; i++) {
if (nums[i] > maxVal){
maxVal = nums[i];
maxIndex = i;
}
}
TreeNode root = new TreeNode(maxVal);
// 根据maxIndex划分左右子树
root.left = constructMaximumBinaryTree1(nums, leftIndex, maxIndex);
root.right = constructMaximumBinaryTree1(nums, maxIndex + 1, rightIndex);
return root;
}
}
617.合并二叉树
题目
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
思路
递归三部曲
1.确定返回值和参数:这里返回值设置为新创建的节点node,参数为root1,root2。
2.确定终止条件:都为空,返回null;有不空,返回node。
3.确定单层递归逻辑:root1非空,node=root1;root2非空,node=root2;都非空,node=new TreeNode(root1.val+root2.val);然后node.left递归,node.right递归。
代码如下:
class Solution {
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
if (root1 == null && root2 == null) return null;
TreeNode node;
if (root1 != null && root2 == null) {
node = new TreeNode(root1.val);
node.left = mergeTrees(root1.left, null);
node.right = mergeTrees(root1.right, null);
} else if (root1 == null && root2 != null) {
node = new TreeNode(root2.val);
node.left = mergeTrees(null, root2.left);
node.right = mergeTrees(null, root2.right);
} else {
node = new TreeNode(root1.val + root2.val);
node.left = mergeTrees(root1.left, root2.left);
node.right = mergeTrees(root1.right, root2.right);
}
return node;
}
}
700.二叉搜索树中的搜索
题目
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
思路
递归三部曲:
1.确定返回值和参数:返回节点;参数为节点、输入值。
2.确定终止条件:节点为空,返回空;节点值等于输入值,返回节点。
3.确定递归体:定义左节点、右节点。得到左节点非空则返回左节点;右节点非空则返回右节点;否则返回空。
代码如下:
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
if(root==null) return null;
if(root.val==val) return root;
TreeNode left_node=searchBST(root.left,val);
TreeNode right_node=searchBST(root.right,val);
if(left_node!=null) return left_node;
else if(right_node!=null) return right_node;
else return null;
}
}
代码随想录笔记
二叉树是有序的。。。
递归法
1.确定递归函数的参数和返回值
递归函数的参数传入的就是根节点和要搜索的数值,返回的就是以这个搜索数值所在的节点。
2.确定终止条件
如果root为空,或者找到这个数值了,就返回root节点。
3.确定单层递归的逻辑
看看二叉搜索树的单层递归逻辑有何不同。
因为二叉搜索树的节点是有序的,所以可以有方向的去搜索。
如果root.val > val,搜索左子树,如果root.val < val,就搜索右子树,最后如果都没有搜索到,就返回NULL。
代码如下:
class Solution {
// 递归,利用二叉搜索树特点,优化
public TreeNode searchBST(TreeNode root, int val) {
if (root == null || root.val == val) {
return root;
}
if (val < root.val) {
return searchBST(root.left, val);
} else {
return searchBST(root.right, val);
}
}
}
98.验证二叉搜索树
题目
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
思路
判断中序遍历结果是否是递增的,如果是返回true;如果不是,返回false。
代码如下:
class Solution {
List<Integer> list=new ArrayList<>();
public boolean isValidBST(TreeNode root) {
if(root==null) return true;
traversal(root);
for(int i=1;i<list.size();i++){
if(list.get(i)<=list.get(i-1)) return false;
}
return true;
}
private void traversal(TreeNode root){
if(root.left!=null) traversal(root.left);
list.add(root.val);
if(root.right!=null) traversal(root.right);
return;
}
}
代码随想录笔记
这道题目比较容易陷入两个陷阱:
陷阱1
不能单纯的比较左节点小于中间节点,右节点大于中间节点就完事了。
我们要比较的是 左子树所有节点小于中间节点,右子树所有节点大于中间节点。
陷阱2
样例中最小节点 可能是int的最小值,如果这样使用最小的int来比较也是不行的。
此时可以初始化比较元素为longlong的最小值。
问题可以进一步演进:如果样例中根节点的val 可能是longlong的最小值 又要怎么办呢?
递归三部曲:
1.确定递归函数,返回值以及参数
我们在寻找一个不符合条件的节点,如果没有找到这个节点就遍历了整个树,如果找到不符合的节点了,立刻返回。
2.确定终止条件
如果是空节点 是不是二叉搜索树呢?
是的,二叉搜索树也可以为空!
3.确定单层递归的逻辑
中序遍历,一直更新maxVal,一旦发现maxVal >= root.val,就返回false,注意元素相同时候也要返回false。
class Solution {
// 递归
TreeNode max;
public boolean isValidBST(TreeNode root) {
if (root == null) {
return true;
}
// 左
boolean left = isValidBST(root.left);
if (!left) {
return false;
}
// 中
if (max != null && root.val <= max.val) {
return false;
}
max = root;
// 右
boolean right = isValidBST(root.right);
return right;
}
}
// 简洁实现·递归解法
class Solution {
public boolean isValidBST(TreeNode root) {
return validBST(Long.MIN_VALUE, Long.MAX_VALUE, root);
}
boolean validBST(long lower, long upper, TreeNode root) {
if (root == null) return true;
if (root.val <= lower || root.val >= upper) return false;
return validBST(lower, root.val, root.left) && validBST(root.val, upper, root.right);
}
}
// 简洁实现·中序遍历
class Solution {
private long prev = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root) {
if (root == null) {
return true;
}
if (!isValidBST(root.left)) {
return false;
}
if (root.val <= prev) { // 不满足二叉搜索树条件
return false;
}
prev = root.val;
return isValidBST(root.right);
}
}
530.二叉搜索树的最小绝对差
题目
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。
思路
二叉搜索树的中序遍历为有序的,因此最小差值必为某两个相邻之差。
代码如下:
class Solution {
List<Integer> list=new ArrayList<>();
public int getMinimumDifference(TreeNode root) {
if(root==null) return 0;
traversal(root);
int min=list.get(list.size()-1);
for(int i=1;i<list.size();i++){
if(min>=list.get(i)-list.get(i-1)) min=list.get(i)-list.get(i-1);
}
return min;
}
private void traversal(TreeNode root){
if(root.left!=null) traversal(root.left);
list.add(root.val);
if(root.right!=null) traversal(root.right);
}
}
代码随想录笔记
class Solution {
TreeNode pre;// 记录上一个遍历的结点
int result = Integer.MAX_VALUE;
public int getMinimumDifference(TreeNode root) {
if(root==null)return 0;
traversal(root);
return result;
}
public void traversal(TreeNode root){
if(root==null)return;
//左
traversal(root.left);
//中
if(pre!=null){
result = Math.min(result,root.val-pre.val);
}
pre = root;
//右
traversal(root.right);
}
}
边递归边比较。
501.二叉搜索树的众数
题目
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树
思路
思路一:将BST的节点以及值出现次数存入map中,然后从map中根据value选取key。
代码如下:
class Solution {
public int[] findMode(TreeNode root) {
Map<Integer, Integer> map = new HashMap<>();
List<Integer> list = new ArrayList<>();
if (root == null) return list.stream().mapToInt(Integer::intValue).toArray();
// 获得频率 Map
searchBST(root, map);
List<Map.Entry<Integer, Integer>> mapList = map.entrySet().stream()
.sorted((c1, c2) -> c2.getValue().compareTo(c1.getValue()))
.collect(Collectors.toList());
list.add(mapList.get(0).getKey());
// 把频率最高的加入 list
for (int i = 1; i < mapList.size(); i++) {
if (mapList.get(i).getValue() == mapList.get(i - 1).getValue()) {
list.add(mapList.get(i).getKey());
} else {
break;
}
}
return list.stream().mapToInt(Integer::intValue).toArray();
}
void searchBST(TreeNode curr, Map<Integer, Integer> map) {
if (curr == null) return;
map.put(curr.val, map.getOrDefault(curr.val, 0) + 1);
searchBST(curr.left, map);
searchBST(curr.right, map);
}
}
步骤为:
创建一个空的哈希映射 map,用于存储节点值和它们出现的频率。
创建一个空的整数列表 list,用于存储出现频率最高的节点值。
如果根节点 root 为空,直接返回空列表。
调用 searchBST 方法来遍历二叉树,计算每个节点值的频率,并将结果存储在 map 中。
将 map 的键值对转换为列表 mapList,按照值的降序排序。
将 mapList 中频率最高的节点值加入到 list 中。
遍历剩余的 mapList,如果当前节点值的频率与前一个节点值的频率相同,则将其加入 list,否则结束循环。
将 list 转换为整数数组并返回。
函数 searchBST 的作用是在二叉树中进行深度优先搜索。对于当前节点 curr,将其值与 map 中对应键的值进行更新,如果键不存在则默认为0。然后递归地调用 searchBST 来处理当前节点的左子树和右子树。
思路二:中序遍历时是有序的,边遍历边比较当前节点值与前一节点值是否相同,相同则次数count+1。比较cout与countmax的大小,如果等于,则加入;大于则清空list。
代码如下:
class Solution {
int count;//当前节点值出现的次数
int maxcount;//出现最多的次数
List<Integer> list=new ArrayList<>();//用来存储出现次数最多的节点的值
TreeNode pre;//用来存储前一节点
public int[] findMode(TreeNode root) {
count=0;
maxcount=0;
pre=null;
traversal(root);
int[] res = new int[list.size()];
for (int i = 0; i < list.size(); i++) {
res[i] = list.get(i);
}
return res;
}
public void traversal(TreeNode root){
if(root==null) return;
traversal(root.left);
if(pre==null||root.val!=pre.val) count=0;
else count++;
if(count>maxcount){
list.clear();
list.add(root.val);
maxcount=count;
}else if(count==maxcount){
list.add(root.val);
}
pre=root;
traversal(root.right);
return;
}
}
236.二叉树的最近公共祖先
题目
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
思路

递归三部曲:
1.确定递归函数返回值以及参数
需要递归函数返回值,来告诉我们是否找到节点q或者p
2.确定终止条件
遇到空的话,因为树都是空了,所以返回空。
如果 rootq或者rootp,说明找到 q p ,则将其返回,这个返回值,后面在中节点的处理过程中会用到。
3.确定单层递归逻辑
值得注意的是 本题函数有返回值,是因为回溯的过程需要递归函数的返回值做判断,但本题我们依然要遍历树的所有节点。
如果left 和 right都不为空,说明此时root就是最近公共节点。这个比较好理解
如果left和right都为空,则返回left或者right都是可以的,也就是返回空。
如果left为空,right不为空,就返回right,说明目标节点是通过right返回的,反之依然。
代码如下:
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
return traversal(root,p,q);
}
public TreeNode traversal(TreeNode root,TreeNode p,TreeNode q){
//终止条件
if(root==null||root==p||root==q) return root;
//后序遍历
TreeNode left=traversal(root.left,p,q);
TreeNode right=traversal(root.right,p,q);
//判断左右子节点的返回值
if(left!=null&&right!=null) return root;//说明本身就是最近的公共祖先
else if(left!=null&&right==null) return left;//说明左节点找到p或者q
else if(left==null&&right!=null) return right;
else return null;
}
}
总结
1.求最小公共祖先,需要从底向上遍历,那么二叉树,只能通过后序遍历(即:回溯)实现从底向上的遍历方式。
2.在回溯的过程中,必然要遍历整棵二叉树,即使已经找到结果了,依然要把其他节点遍历完,因为要使用递归函数的返回值(也就是代码中的left和right)做逻辑判断。
3.要理解如果返回值left为空,right不为空为什么要返回right,为什么可以用返回right传给上一层结果。
235.二叉搜索树的最近公共祖先
题目
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
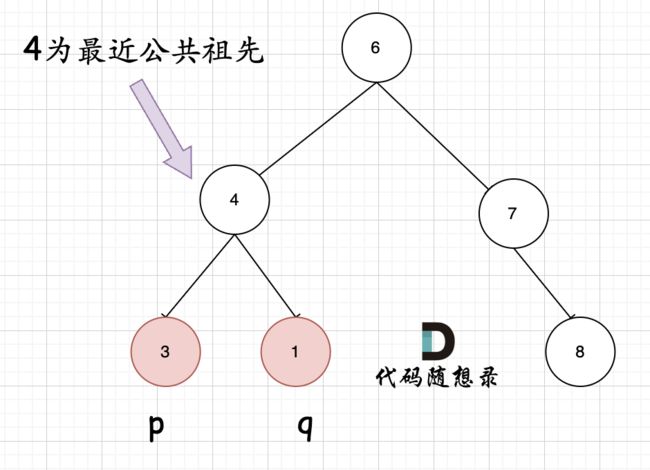
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
思路
二叉搜索树的中序遍历是有序的。传入当前root,比较p,q,root.val,如果p
1.确定递归函数的返回值和传入参数:返回值为TreeNode型,传入参数为root,p,q
2.确定递归函数的终止条件:如果root为空,返回null;如果p
代码如下:
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null) return null;
if((p.val<=root.val&&q.val>=root.val)||(q.val<=root.val&&p.val>=root.val)) return root;
else if((p.val<q.val&&q.val<root.val)||(q.val<p.val&&p.val<root.val)) return lowestCommonAncestor(root.left,p,q);
else return lowestCommonAncestor(root.right,p,q);
}
}
代码随想录笔记
因为是有序树,所有 如果 中间节点是 q 和 p 的公共祖先,那么 中节点的数组 一定是在 [p, q]区间的。即 中节点 > p && 中节点 < q 或者 中节点 > q && 中节点 < p。
那么只要从上到下去遍历,遇到 cur节点是数值在[p, q]区间中则一定可以说明该节点cur就是q 和 p的公共祖先。 那问题来了,一定是最近公共祖先吗?
当我们从上向下去递归遍历,第一次遇到 cur节点是数值在[p, q]区间中,那么cur就是 p和q的最近公共祖先。
递归三部曲如下:
1.确定递归函数返回值以及参数
参数就是当前节点,以及两个结点 p、q。返回值是要返回最近公共祖先,所以是TreeNode。
2.确定终止条件
遇到空返回就可以了,其实都不需要这个终止条件,因为题目中说了p、q 为不同节点且均存在于给定的二叉搜索树中。也就是说一定会找到公共祖先的,所以并不存在遇到空的情况。
3.确定单层递归的逻辑
需要注意的是此时不知道p和q谁大,所以两个都要判断
精简代码如下:
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left, p, q);
if (root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right, p, q);
return root;
}
}
701.二叉搜索树中的插入操作
题目
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
思路
给定val,与root.val比较,如果root.val大于val,则将root.left和val进行递归;反之将root.right和val进行递归。
递归三部曲如下:
1.确定递归函数的返回值和参数类型:返回TreeNode,参数类型为TreenNode和int
2.确定递归函数的终止条件:如果root为空,则返回构造一个节点,值为val;
3.确定递归体:如果root.val大于val,则将root.left和val进行递归;反之将root.right和val进行递归。最后返回root。
代码如下:
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
if(root==null) return new TreeNode(val);
if(root.val>val) root.left=insertIntoBST(root.left,val);
if(root.val<val) root.right=insertIntoBST(root.right,val);
return root;
}
}
450.删除二叉搜索树中的节点
题目
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点;
如果找到了,删除它。
代码随想录思路
递归三部曲:
1.确定递归函数参数以及返回值
2.确定终止条件
遇到空返回,其实这也说明没找到删除的节点,遍历到空节点直接返回了
3.确定单层递归的逻辑
这里就把二叉搜索树中删除节点遇到的情况都搞清楚。
有以下五种情况:
第一种情况:没找到删除的节点,遍历到空节点直接返回了
找到删除的节点:
第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
第三种情况:删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点
第四种情况:删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
第五种情况:左右孩子节点都不为空,则将删除节点的左子树头结点(左孩子)放到删除节点的右子树的最左面节点的左孩子上,返回删除节点右孩子为新的根节点。
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if(root==null) return null;
if(root.val>key) root.left=deleteNode(root.left,key);
else if(root.val<key) root.right=deleteNode(root.right,key);
else if(root.val==key){
if(root.left==null&&root.right==null) return null;
else if(root.left==null) return root.right;
else if(root.right==null) return root.left;
else{
TreeNode left=root.left;
TreeNode right=root.right;
while(right.left!=null){
right=right.left;
}
right.left=left;
return root.right;
}
}
return root;
}
}
669.修剪二叉搜索树
题目
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
思路
递归三部曲
1.确定递归函数的返回值类型和参数
2.确定递归函数的终止条件:如果为空,则返回空
3.确定递归体:如果root.val
代码如下:
class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
if(root==null) return null;
if(root.val<low){
return trimBST(root.right,low,high);
} else if(root.val>high){
return trimBST(root.left,low,high);
}else{
root.left=trimBST(root.left,low,high);
root.right=trimBST(root.right,low,high);
}
return root;
}
}
这里需要注意的点是当root.val
108.将有序数组转换为二叉搜索树
题目
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
思路
本题思路很容易想到,即每次选取给定数组的中间那个元素作为根节点,该节点的左子树为递归数组中间元素左边部分的结果,右子树为递归数组中间元素右边的结果。注意coding时传入数组起始点、终止点的数值,很容易出现错误。
代码如下:
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
if (nums.length == 0) return null;
TreeNode root = new TreeNode(nums[nums.length / 2]);
root.left = traversal(nums, 0, nums.length / 2 - 1);
root.right = traversal(nums, nums.length / 2 + 1, nums.length - 1);
return root;
}
public TreeNode traversal(int[] nums, int begin, int end) {
if (begin > end) return null;
int middle = (begin + end) / 2;
TreeNode root = new TreeNode(nums[middle]);
root.left = traversal(nums, begin, middle - 1);
root.right = traversal(nums, middle + 1, end);
return root;
}
}
代码随想录笔记
注意区间是左闭右闭还是左闭右开
代码如下:
递归: 左闭右开 [left,right)
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return sortedArrayToBST(nums, 0, nums.length);
}
public TreeNode sortedArrayToBST(int[] nums, int left, int right) {
if (left >= right) {
return null;
}
if (right - left == 1) {
return new TreeNode(nums[left]);
}
int mid = left + (right - left) / 2;
TreeNode root = new TreeNode(nums[mid]);
root.left = sortedArrayToBST(nums, left, mid);
root.right = sortedArrayToBST(nums, mid + 1, right);
return root;
}
}
递归: 左闭右闭 [left,right]
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
TreeNode root = traversal(nums, 0, nums.length - 1);
return root;
}
// 左闭右闭区间[left, right]
private TreeNode traversal(int[] nums, int left, int right) {
if (left > right) return null;
int mid = left + ((right - left) >> 1);
TreeNode root = new TreeNode(nums[mid]);
root.left = traversal(nums, left, mid - 1);
root.right = traversal(nums, mid + 1, right);
return root;
}
}
538.把二叉搜索树转换为累加树
题目
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。
代码随想录笔记
没思路,直接看答案。
本题依然需要一个pre指针记录当前遍历节点cur的前一个节点,这样才方便做累加。
1.递归函数参数以及返回值
这里很明确了,不需要递归函数的返回值做什么操作了,要遍历整棵树。
同时需要定义一个全局变量pre,用来保存cur节点的前一个节点的数值,定义为int型就可以了。
2.确定终止条件
遇空就终止。
3.确定单层递归的逻辑
注意要右中左来遍历二叉树, 中节点的处理逻辑就是让cur的数值加上前一个节点的数值。
代码如下:
class Solution {
int pre;
public TreeNode convertBST(TreeNode root) {
pre=0;
traversal(root);
return root;
}
public void traversal(TreeNode root){
if(root==null) return;
//右中左
traversal(root.right);
root.val=pre+root.val;
pre=root.val;
traversal(root.left);
}
}
注意
首先确定遍历顺序为右中左,然后需要设置一个变量保存上一个节点的值,最后这里直接修改节点数值即可。
77.组合
题目
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
代码随想录思路
第一次做回溯,想了半天连终止条件都想不出来,直接看答案。
回溯三部曲:
1.递归函数的返回值以及参数
在这里要定义两个全局变量,一个用来存放符合条件单一结果,一个用来存放符合条件结果的集合。
函数里一定有两个参数,既然是集合n里面取k个数,那么n和k是两个int型的参数。
然后还需要一个参数,为int型变量startIndex,这个参数用来记录本层递归的中,集合从哪里开始遍历
2.回溯函数终止条件
path这个数组的大小如果达到k,说明我们找到了一个子集大小为k的组合了,在图中path存的就是根节点到叶子节点的路径。
3.单层搜索的过程
for循环每次从startIndex开始遍历,然后用path保存取到的节点i。
可以看出backtracking(递归函数)通过不断调用自己一直往深处遍历,总会遇到叶子节点,遇到了叶子节点就要返回。
backtracking的下面部分就是回溯的操作了,撤销本次处理的结果。
代码如下:
class Solution {
List<Integer> path=new ArrayList<>();
List<List<Integer>> result=new ArrayList<>();
public List<List<Integer>> combine(int n, int k) {
backtracking(n,k,1);
return result;
}
public void backtracking(int n,int k,int startIndex){
//终止条件
if(path.size()==k){
result.add(new ArrayList(path));
return;
}
//回溯体
for(int i=startIndex;i<=n;i++){
path.add(i);
backtracking(n,k,i+1);
//回溯
path.remove(path.size()-1);
}
return;
}
}
216.组合总和Ⅲ
题目
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
只使用数字1到9
每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
思路
比如n=9,k=3。首先进1,然后进2,然后进3,不行,回溯,进4,不行,回溯。。。进6,行,存入list,return。然后进3,然后进4,不行,回溯。。。。
回溯三部曲:
1.递归函数的参数及返回值
参数:需要n,k,index以及target。其中index是刚才加入的数值,target用来判断是否满足要求。没有返回值。
2.回溯函数的终止条件
当list的长度等于k则终止,且target=index,则将list加入result。
3.单层搜索的过程
for从index+1开始,list保存节点,递归,回溯。
代码如下:
class Solution {
List<Integer> list=new ArrayList<>();
List<List<Integer>> result=new ArrayList<>();
public List<List<Integer>> combinationSum3(int k, int n) {
backtracking(k,n,0,n);
return result;
}
public void backtracking(int k,int n,int x,int target){
//终止条件
if(list.size()==k){
if(target==x) result.add(new ArrayList(list));
return;
}
//递归体
for(int i=x+1;i<=9;i++){
list.add(i);
backtracking(k,n,i,target-x);
list.remove(list.size()-1);
}
return;
}
}
代码随想录代码:
class Solution {
List<Integer> list=new ArrayList<>();
List<List<Integer>> result=new ArrayList<>();
public List<List<Integer>> combinationSum3(int k, int n) {
backtracking(k,n,0,n);
return result;
}
public void backtracking(int k,int n,int x,int target){
//终止条件
if(list.size()==k){
if(target==x) result.add(new ArrayList(list));
return;
}
//递归体
for(int i=x+1;i<=9;i++){
list.add(i);
backtracking(k,n,i,target-x);
list.remove(list.size()-1);
}
return;
}
}
17.电话号码的字母组合
题目
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
思路
本题思路很简单。首先定义一个map
回溯三部曲:
1.确定回溯函数参数
首先需要一个字符串s来收集叶子节点的结果,然后用一个字符串数组result保存起来,这两个变量我依然定义为全局。
再来看参数,参数指定是有题目中给的string digits,然后还要有一个参数就是int型的index。
这个index是记录遍历第几个数字了,就是用来遍历digits的(题目中给出数字字符串),同时index也表示树的深度。
2.确定终止条件
那么终止条件就是如果index 等于 输入的数字个数(digits.size)了(本来index就是用来遍历digits的)。
然后收集结果,结束本层递归。
3.确定单层遍历逻辑
首先要取index指向的数字,并找到对应的字符集(手机键盘的字符集)。
然后for循环来处理这个字符集。
代码如下:
class Solution {
//设置全局列表存储最后的结果
List<String> list = new ArrayList<>();
public List<String> letterCombinations(String digits) {
if (digits == null || digits.length() == 0) {
return list;
}
//初始对应所有的数字,为了直接对应2-9,新增了两个无效的字符串""
String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
//迭代处理
backTracking(digits, numString, 0);
return list;
}
//每次迭代获取一个字符串,所以会设计大量的字符串拼接,所以这里选择更为高效的 StringBuild
StringBuilder temp = new StringBuilder();
//比如digits如果为"23",num 为0,则str表示2对应的 abc
public void backTracking(String digits, String[] numString, int num) {
//遍历全部一次记录一次得到的字符串
if (num == digits.length()) {
list.add(temp.toString());
return;
}
//str 表示当前num对应的字符串
String str = numString[digits.charAt(num) - '0'];
for (int i = 0; i < str.length(); i++) {
temp.append(str.charAt(i));
//c
backTracking(digits, numString, num + 1);
//剔除末尾的继续尝试
temp.deleteCharAt(temp.length() - 1);
}
}
}
自己代码用map写的,代码如下:
class Solution {
StringBuilder path = new StringBuilder();
Map<Character, String> map;
List<String> result;
public List<String> letterCombinations(String digits) {
map = new HashMap<>();
map.put('2', "abc");
map.put('3', "def");
map.put('4', "ghi");
map.put('5', "jkl");
map.put('6', "mno");
map.put('7', "pqrs");
map.put('8', "tuv");
map.put('9', "wxyz");
result = new ArrayList<>();
if (digits.length() == 0)
return result;
backtracking(digits, 0);
return result;
}
public void backtracking(String digits, int index) {
if (index == digits.length()) {
result.add(path.toString());
return;
}
String s = map.get(digits.charAt(index));
for (int i = 0; i < s.length(); i++) {
path.append(s.charAt(i));
backtracking(digits, index + 1);
path.deleteCharAt(path.length() - 1);
}
}
}
本题的问题在于怎么存数据,然后怎么回溯。做的时候并没有学String、StringBuilder、StringBuffer,因此没想到。补充如下:
添加链接描述
StringBuilder和StringBuffer能对字符串进行修改。
由于 StringBuilder 相较于 StringBuffer 有速度优势,多数情况下建议使用 StringBuilder类。然而在应用程序要求线程安全的情况下,则必须使用 StringBuffer 类。
39.组合总和
题目
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
思路
本题是从一个数组中选取,因此在递归中需要引入startIndex。注意本题数组中的每个元素都可以多次选取,而且没有0,因此for循环每次都要从startIndex开始。
1.确定递归函数的返回类型和参数。返回类型为void,参数为candidates,target,startIndex,sum。
2.确定递归函数的终止条件。如果sum==target,则将list加入result,然后返回;如果sum>target,则返回。
3.确定递归函数的递归体。从startIndex开始,加入list,sum增加,递归;回溯。
代码如下:
class Solution {
List<Integer> list=new ArrayList<>();
List<List<Integer>> result=new ArrayList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
if(candidates.length==0) return result;
backtracking(candidates,target,0,0);
return result;
}
public void backtracking(int[] candidates, int target, int startIndex,int sum){
//终止条件
if(sum==target){
result.add(new ArrayList(list));
return;
}else if(sum>target){
return;
}
//递归体
for(int i=startIndex;i<candidates.length;i++){
list.add(candidates[i]);
sum=sum+candidates[i];
backtracking(candidates,target,i,sum);
//回溯
sum=sum-candidates[i];
list.remove(list.size()-1);
}
return;
}
}
代码随想录参考代码:
// 剪枝优化
class Solution {
public List<List<Integer>> combinationSum(int[] candidates, int target) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(candidates); // 先进行排序
backtracking(res, new ArrayList<>(), candidates, target, 0, 0);
return res;
}
public void backtracking(List<List<Integer>> res, List<Integer> path, int[] candidates, int target, int sum, int idx) {
// 找到了数字和为 target 的组合
if (sum == target) {
res.add(new ArrayList<>(path));
return;
}
for (int i = idx; i < candidates.length; i++) {
// 如果 sum + candidates[i] > target 就终止遍历
if (sum + candidates[i] > target) break;
path.add(candidates[i]);
backtracking(res, path, candidates, target, sum + candidates[i], i);
path.remove(path.size() - 1); // 回溯,移除路径 path 最后一个元素
}
}
}
40.组合总和Ⅱ
题目
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
思路
本题主要难点在于如何在回溯中区分树层去重和树枝去重。因为纵向数字重复是合法的,但是横向数字重复是我们需要避免的。这里用used数组来标记每个元素是否被使用。首先对元素进行排序,然后定义used数字来标记数字,使用了就为1,没使用就是0.当当前取的元素与前一个相同,且前一个没有使用,则是数层去重,我们要避免。将这一步描述为if(i>=1&&candidates[i-1]==candidates[i]&&used[i-1]==false) continue;
因此代码如下:
class Solution {
List<Integer> path=new ArrayList<>();
List<List<Integer>> result=new ArrayList<>();
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates);
boolean[] used=new boolean[candidates.length];
backtracking(candidates,target,used,0,0);
return result;
}
public void backtracking(int[] candidates, int target, boolean[] used, int startIndex, int sum){
if(sum>target) return;
else if(sum==target){
result.add(new ArrayList(path));
return;
}
for(int i=startIndex;i<candidates.length;i++){
if(i>=1&&candidates[i-1]==candidates[i]&&used[i-1]==false) continue;
path.add(candidates[i]);
sum=sum+candidates[i];
used[i]=true;
backtracking(candidates,target,used,i+1,sum);
used[i]=false;
sum=sum-candidates[i];
path.remove(path.size()-1);
}
return;
}
}
376.摆动序列
题目
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
例如, [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ,因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
相反,[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
思路
贪心算法:挑选局部最优,最终达到全局最优。
所以关键就是想什么是局部最优,感觉很难。
本题如图

可以明显看到,局部最优就是每次删除单调坡度上的节点。
然后,本题具体需要考虑三种情况:
情况一:上下坡中有平坡
情况二:数组首尾两端
情况三:单调坡度有平坡
完整代码为:
class Solution {
public int wiggleMaxLength(int[] nums) {
if (nums.length <= 1) {
return nums.length;
}
//当前差值
int curDiff = 0;
//上一个差值
int preDiff = 0;
int count = 1;
for (int i = 1; i < nums.length; i++) {
//得到当前差值
curDiff = nums[i] - nums[i - 1];
//如果当前差值和上一个差值为一正一负
//等于0的情况表示初始时的preDiff
if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {
count++;
preDiff = curDiff;
}
}
return count;
}
}
55.跳跃游戏
题目
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
思路
这道题目关键点在于:不用拘泥于每次究竟跳几步,而是看覆盖范围,覆盖范围内一定是可以跳过来的,不用管是怎么跳的。
只要保证:当前在覆盖范围内,且最大覆盖范围能够达到最后一个位置,那么就是true。
代码如下:
class Solution {
public boolean canJump(int[] nums) {
int maxindex=0;
for(int i=0;i<nums.length;i++){
if(maxindex>=nums.length-1) return true;
if(i<=maxindex){
int nowindex=i+nums[i];
if(nowindex>maxindex) maxindex=nowindex;
}else return false;
}
return false;
}
}
45.跳跃游戏
题目
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]
i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
思路
本题看完代码随想录后依然没有理解,经过思考后理解如下:
贪心的思路是使用尽可能小的步数来获得尽可能大的覆盖范围。
首先,问题是每次具体跳到哪才是最小,代码随想录中的方法是设置当前的最大覆盖范围,然后我们一个一个走,一个一个判断他的最大覆盖范围,选择最大的最大覆盖范围即可。但是对应到代码就很难实现,这是我没理解的点。下面根据代码反推思路:
我们需要记录步数result,最大覆盖范围maxcover和当前往下跳一步的最大覆盖范围nextcover。
然后每次i,更新目前的最大覆盖范围maxcover,如果maxcover能到终点,意味着从当前出发再跳一步即可。
然后考察这个当前的i,我们从0位置开始有一个nextcover,按照前面的思路需要去遍历0到nextcover的每一个位置的最大覆盖范围,因此我们可以认为这个当前的i就是我们的遍历步骤。如果当前的i就是nextcover,意味着我们遍历完了,但是依然没有走到终点,所以我们需要再走一步来扩大最大覆盖范围,且nextcover=maxcover(这里最难理解,实际就是刚才我们的整个遍历过程中最大的覆盖范围就是从上一步跳下一步的那个点)。如果当前i不是nextcover,意味着我们需要继续遍历,那么开始i++进行下一次遍历即可。
代码如下:
class Solution {
public int jump(int[] nums) {
if (nums == null || nums.length == 0 || nums.length == 1) {
return 0;
}
int maxcover=0;
int result=0;
int nextcover=0;
for(int i=0;i<nums.length;i++){
maxcover=Math.max(maxcover,i+nums[i]);
if(maxcover>=nums.length-1){
result++;
break;
}
if(i==nextcover){
nextcover=maxcover;
result++;
}
}
return result;
}
}
135.分发糖果
题目
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
你需要按照以下要求,给这些孩子分发糖果:
每个孩子至少分配到 1 个糖果。
相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
思路
分两个阶段
1、起点下标1 从左往右,只要 右边 比 左边 大,右边的糖果=左边 + 1
2、起点下标 ratings.length - 2 从右往左, 只要左边 比 右边 大,此时 左边的糖果应该 取本身的糖果数(符合比它左边大) 和 右边糖果数 + 1 二者的最大值,这样才符合 它比它左边的大,也比它右边大
注:两边兼顾则很可能会混乱
代码如下:
class Solution {
public int candy(int[] ratings) {
int[] sum=new int[ratings.length];
for(int i=0;i<ratings.length;i++){
if(i>0&&ratings[i]>ratings[i-1]){
sum[i]=sum[i-1]+1;
}else{
sum[i]=1;
}
}
for(int j=ratings.length-1;j>=0;j--){
if(j<ratings.length-1&&ratings[j]>ratings[j+1]&&sum[j]<=sum[j+1]){
sum[j]=sum[j+1]+1;
}
}
return Arrays.stream(sum).sum();
}
}
406.根据身高重建队列
题目
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
思路
本题与135题类似,先确定一个维度,再确定另一个维度。步骤如下:
Step1:根据身高h从大到小排序,这样people[i]前面的人一定身高大于等于自身
Step2:根据k逐个插值到队列中,如people[i]=[5,2]则将其插入索引为2的位置上
class Solution {
public int[][] reconstructQueue(int[][] people) {
Arrays.sort(people,(e1,e2)->{
if(e1[0]==e2[0]) return e1[1]-e2[1];
else return e2[0]-e1[0];
});
List<int[]> queue=new ArrayList<>();
for(int i=0;i<people.length;i++){
queue.add(people[i][1],people[i]);
}
return queue.toArray(new int[people.length][]);
}
}
452.用最少数量的箭引爆气球
题目
有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ,其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。
一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后,可以无限地前进。
给你一个数组 points ,返回引爆所有气球所必须射出的 最小 弓箭数 。
思路
本题思路比较简单,即按xend排序,然后重叠的用一支箭射,但是代码实现比较复杂。
1.排序中不能之间简单返回e1[1]-e2[1],因为会出现溢出,如输入[[-2147483646,-2147483645],[2147483646,2147483647]]
2.需要不断记录当前这支箭最大x位置(即重叠气球中最小的xend)
代码如下:
class Solution {
public int findMinArrowShots(int[][] points) {
if (points == null || points.length == 0) {
return 0;
}
Arrays.sort(points, (e1, e2) -> Integer.compare(e1[1], e2[1]));
int arrowCount = 1;
int arrowLimit = points[0][1];
for (int i = 1; i < points.length; i++) {
if (points[i][0] > arrowLimit) {
arrowCount++;
arrowLimit = points[i][1];
}
}
return arrowCount;
}
}
763.划分字母区间
题目
给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。
注意,划分结果需要满足:将所有划分结果按顺序连接,得到的字符串仍然是 s 。
返回一个表示每个字符串片段的长度的列表。
思路
可以分为如下两步:
统计每一个字符最后出现的位置
从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点

代码如下:
class Solution {
public List<Integer> partitionLabels(String s) {
List<Integer> result=new ArrayList<>();
int[] flag=new int[27];
for(int i=0;i<s.length();i++){
flag[s.charAt(i)-'a']=i;
}
int left=0;int right=0;
for(int i=0;i<s.length();i++){
right=Math.max(right,flag[s.charAt(i)-'a']);
if(i==right){
result.add(right-left+1);
left=i+1;
}
}
return result;
}
}
505.斐波那契数列
题目
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
思路
《代码随想录》动态规划五部曲:
1.确定dp[i]含义 dp[i]:第i个斐波那契数值为dp[i]
2.递推公式 dp(n) = dp(n - 1) + dp(n - 2),其中 n > 1
3.db数组如何初始化 dp(0) = 0,dp(1) = 1
4.遍历顺序
5.打印数组
70.爬楼梯
题目
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
思路
由于刚开始学习,因此思路并不一定完全正确,只是当前的总结。
动态规划类题目通常当前结果依赖于之前的结果,因此思路从这里开始,可以思考的出递推公式
本题:n阶可以由n-1阶跨1步加上n-2阶跨2步得到,因此n阶方法等于n-1阶方法加上n-2阶方法。
96.不同地二叉搜索树
题目
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
思路
以n=3为例,二叉搜索树个数=以1为头节点的二叉搜索树个数+以2为头节点的二叉搜索树个数+以3为头节点的二叉搜索树个数
以1为头节点的二叉搜索树个数=左子树节点个数为0的二叉搜索树个数×右子树节点个数为2的二叉搜索树个数
以2为头节点的二叉搜索树个数=左子树节点个数为1的二叉搜索树个数×右子树节点个数为1的二叉搜索树个数
以3为头节点的二叉搜索树个数=左子树节点个数为2的二叉搜索树个数×右子树节点个数为0的二叉搜索树个数
而节点个数为0的二叉搜索树个数,节点个数为1的二叉搜索树个数,节点个数为2的二叉搜索树个数不就是dp[0],dp[1],dp[2]嘛!
所以递推式就呼之欲出了!