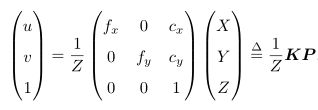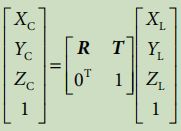【传感器标定】路侧激光雷达和相机的标定(1)

1.前言

        这里要描叙的场景比较简单，就是在路口矗立着路杆，杆子上面安装了多路摄像机,激光雷达和毫米波雷达。其中，摄像机用来提供目标的语义信息(如:行人,车辆等)，激光雷达可以提供目标的位置和形状(三维)信息，而毫米波雷达可以比较准确地测量目标的速度。因此，采用以上多传感器融合，可以全方位地掌握路口目标的状态。在设计具体的融合算法之前要先进行传感器之间的联合标定。最近实验只需要用到激光雷达和摄像头，这里暂且值谈论激光雷达和相机的联合标定，更确切地说就是讨论激光雷达到图像的转换关系。这里的转换关系既涉及到激光雷达坐标系(三维)到相机坐标坐标系(三维)的转化，同时还设计到相机坐标系(三维)到图像(像素坐标系,二维)的转换。前一个转化我们说是激光雷达到相机的外参的标定，后一个转化是相机的内参的标定。通常认为相机的内参在出场之后是固定的，不会在使用过程中发生变化。

2. 坐标系转换

1). 相机坐标系到图像坐标系的转换        

        相机坐标系用来描叙物体相对相机的位置，相机固定以后相机坐标系的原点也就确定了，相机坐标系的原点为相机光心O点，相机坐标系中的坐标为(Xc,Yc,Zc)。图像坐标系是为了方便描叙成像过程中物体由相机坐标系(三维)到图像坐标系(二维)的投影投射关系而引入，而且可以方便进一步计算得到像素坐标系下的坐标，图像坐标系的单位同相机坐标系都为m。我们先引出小孔成像模型来描叙物体的成像过程。设为相机坐标系，按右手法则，习惯上让轴指向相机前方，向右，向下。为摄像机的光心，也是针孔模型中的针孔。现实世界的空间点，经过小孔投影之后，落在物理成像平面上，成像点为 。设的坐标为，为，并且设物理成像平面到小孔的距离为（焦距）。根据三角形相似关系

其中负号表示成的像是倒立的，为了让模型更符合实际(实际相机得到的像当然不是倒立的)，可以等价地把成像平面对称地放置在相机的前方，这样可以把负号去掉。

这里借用了一种数学模型的方式来描叙相机坐标系中的点与成像平面投影位置之间的关系。

2).图像坐标系到像素坐标系的转换

        在相机中，我们最终获得的是一个个的像素，而成像平面仍然是一个物理平面(单位为m)，所以我们还需要在成像平面上对像进行采样和量化。为了描叙传感器将感受到的光线转换到图像像素的过程，设在物理成像平面上固定着一个像素平面 o−u−v。在像素平面得到了 P ′ 的像素坐标：[u,v] T 。其中像素坐标系 x 的定义方式是：原点 o ′ 位于图像的左上角，u 轴向右与 x 轴平行，v轴向下与 y 轴平行。像素坐标系与成像平面之间，相差了一个缩放和一个原点的平移。设像素坐标在 u 轴上缩放了 α 倍，在 v 上缩放了 β 倍。同时，原点平移了 [c x ,c y ] T 。那么，P ′ 的坐标与像素坐标 [u,v] T 的关系为

将上面两个式子合并

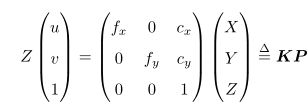
其中，f 的单位为米，α,β 的单位为像素每米，所以 f x ,f y 的单位为像素。利用齐次坐标，将上式写成简洁的矩阵形式

或者

其中的K称之为相机的内参数矩阵，通常借助于"张氏标定法"来计算相机的内参。

void LoadCoordMap(std::string calibrationFile, cv::Size image_size, cv::OutputArray mapx, cv::OutputArray &mapy)
{
    cv::FileStorage fs1(calibrationFile, cv::FileStorage::READ);
    cv::Mat intrinsic = cv::Mat(3, 3, CV_32FC1);
    cv::Mat distCoeffs;
    fs1["intrinsic"] >> intrinsic;
    fs1["distCoeffs"] >> distCoeffs;

    double rate = 1;
    cv::Size outputSize(image_size.width * rate, image_size.height * rate);
    //cout << image_size << endl;
    //cout << outputSize << endl;

    cv::Mat R = cv::Mat::eye(3, 3, CV_32FC1);

    //cout << files.size() << "," << image_Seq.size() << endl;
    //assert(files.size() == image_Seq.size());

    cv::Mat intrinsic_mat(intrinsic), new_intrinsic_mat;
    intrinsic_mat.copyTo(new_intrinsic_mat);
    float p1 = 0.993;
    new_intrinsic_mat.at(0, 0) *= p1;
    new_intrinsic_mat.at(1, 1) *= p1;

    //new_intrinsic_mat.at(0, 2) = 0.5 * image_size.width;
    //new_intrinsic_mat.at(1, 2) = 0.5 * image_size.height;
    cv::initUndistortRectifyMap(intrinsic, distCoeffs, R,
                                getOptimalNewCameraMatrix(new_intrinsic_mat, distCoeffs, image_size, 1, outputSize, 0),
                                outputSize, CV_32FC1, mapx, mapy);
}

void CorrectPicturesDir(const std::string &calibParamsFile, const std::string &inputDir, const std::string &outputDir, cv::Size inputSize) {
	std::vector files;
	cv::glob(inputDir, files);

	// Size image_size = imread(files[0]).size();
	cv::Size image_size = inputSize;
	cv::Mat mapx = cv::Mat(image_size, CV_32FC1);
	cv::Mat mapy = cv::Mat(image_size, CV_32FC1);

	LoadCoordMap(calibParamsFile, image_size, mapx, mapy);
	//initUndistortRectifyMap();
	for (int i = 0; i < files.size(); i++)
	{
		cv::Mat dst;
		cv::Mat image = cv::imread(files[i]);
		cv::resize(image,image,image_size);
		//undistort(image, dst, intrinsic1, distCoeffs1);

		//cv::initUndistortRectifyMap();
		cv::remap(image, dst, mapx, mapy, cv::INTER_LINEAR, cv::BORDER_CONSTANT);

		char buf[256] = {0};
		sprintf(buf,"%d_u.jpg",i);
		std::string dstImgName = buf;
		cv::imwrite(outputDir + "/" + dstImgName, dst);
		//waitKey(1000);
	}
}

int Calibration(std::string calibPicPath,
                cv::Size chessBoardSize,
                std::string calibParamsFile,
                cv::Size inputSize) {
	// load image files
	std::vector files;
	cv::glob(calibPicPath, files);

    std::vector obj;
	int numCornersHor = chessBoardSize.width - 1;
	int numCornersVer = chessBoardSize.height - 1;
	int numSquares = (numCornersHor-1)*(numCornersVer-1);
	for (int i = 0; i < numCornersHor; i++) {
		for (int j = 0; j < numCornersVer; j++) {
		    //world coordinate??
			obj.push_back(cv::Point3f((float)j * numSquares, (float)i * numSquares, 0));
        }
    }

    std::vector> imagePoints;
    std::vector> objectPoints;
    cv::TermCriteria criteria = cv::TermCriteria(cv::TermCriteria::EPS + cv::TermCriteria::MAX_ITER, 30, 0.001);
	for (int i = 0; i < files.size(); i++) {
		printf("image file : %s \n", files[i].c_str());
		cv::Mat image = cv::imread(files[i]);
		cv::resize(image,image,inputSize);
		cv::Mat gray;
		cv::cvtColor(image, gray, cv::COLOR_BGR2GRAY);
		std::vector corners;
		//detect the corners of the chessboard
		bool ret = cv::findChessboardCorners(gray,
                             cv::Size(numCornersVer,numCornersHor), //cv::Size(cols,rows)
                             corners,
                             cv::CALIB_CB_ADAPTIVE_THRESH | cv::CALIB_CB_FILTER_QUADS);
		if (ret) {
			cv::cornerSubPix(gray, corners, cv::Size(11, 11), cv::Size(-1, -1), criteria);
			cv::drawChessboardCorners(image, cv::Size(numCornersVer, numCornersHor), corners, ret); //draw corners in the picture
			imagePoints.push_back(corners);
			objectPoints.push_back(obj);
			
			std::string imageFileName;
			std::stringstream strStm;
			strStm << "./tmp";
			strStm << i + 1;
			strStm >> imageFileName;
			imageFileName += "_corns.jpg";
			cv::imwrite(imageFileName.c_str(),image);
			cv::imshow("calibration-demo", image);
			if (cv::waitKey(-1) > 0) {
			    continue;
			};
		}
		else
			printf("ret:%d;findChessboardCorners fail !!! \n",ret);
	}
	if (0 == imagePoints.size()) {
		std::cout << "no picture can find chessboard coners ... " << std::endl;
		return -1;
	}

	//https://nodyoung.blog.csdn.net/article/details/52287829
	cv::InputArrayOfArrays IMGPOINT = imagePoints;
	printf("%d \n", (int)IMGPOINT.total());
	cv::InputArrayOfArrays OBJPOINT = objectPoints;
	printf("%d \n", (int)OBJPOINT.total());

	for (int i = 0; i < 3; ++i) {
		printf("%d \n", OBJPOINT.getMat(i).checkVector(3, CV_32F));
		printf("%d \n", IMGPOINT.getMat(i).checkVector(2, CV_32F));
	}

	printf("%d pass\n",__LINE__);

    cv::Mat distCoeffs;
	cv::Mat intrinsic = cv::Mat(3, 3, CV_32FC1);
	std::vector rvecs; //rotation vector
	std::vector tvecs; //offset vector
	intrinsic.ptr(0)[0] = 1;
	intrinsic.ptr(1)[1] = 1;
	cv::calibrateCamera(objectPoints, imagePoints, inputSize, intrinsic, distCoeffs, rvecs, tvecs);
	cv::FileStorage fs(calibParamsFile, cv::FileStorage::WRITE);
	fs << "distCoeffs" << distCoeffs;
	fs << "intrinsic" << intrinsic;
	fs << "inputSize" << inputSize;
	fs.release();

	return 0;
}

int main() {
	cv::Size chessBoardSize(8, 7);
	cv::Size inputSize(1920,1080);
    std::string calibParamsFile = "../hikvision_6mm/params/hikvision_6mm.xml";
    std::string calibPicPath = "../hikvision_6mm/pictures"; //
    if (0 == Calibration(calibPicPath, chessBoardSize,calibParamsFile,inputSize)) {
        CorrectPicturesDir(calibParamsFile, calibPicPath, "./tmp", inputSize);
    } else {
        std::cout << "calibration error!!!" << std::endl;
    }
	return 0;
}

角点检测效果图：

3). 雷达坐标系到相机坐标系的转换

        雷达坐标系和相机坐标系都处于三维空间下，但是他们的坐标原点和各个坐标轴的方向不同(这个对于写代码很重要)，所以进行刚体变换就可以了。所谓刚体变换是指在三维空间中，当物体不发生形变时，对一个几何物体做旋转，平移运动。我所用的激光雷达和摄像机坐标系都是右手坐标系(大拇指指向轴线的方向，四指的方向为旋转的正方向)，可以通过刚体变换的方式将激光雷达坐标系转换到相机坐标系。下图为激光雷达坐标系到相机坐标系刚体变换的数学表达式，R表示3x3的旋转矩阵，T表示3x1的平移矩阵。

上面用了齐次坐标的表达方式，拆开来看如下。

直接摆出旋转矩阵R并不直观，很难想象出这个旋转矩阵究竟是什么样子。当他们变换时也不知道物体是在向那个方向转动。借助于欧拉角可以让问题变得更加直观，它使用3个分离的转角来描叙旋转，把一个旋转分解成3次绕不同轴的转动。最终的R就是这3次转动叠加之后的效果，用数学表达时表示就是3个旋转矩阵的乘积。例如，激光雷达坐标系分别绕X轴旋转角度roll(翻滚角)，绕Y轴旋转角度pitch(俯仰角)，绕z轴旋转角度yaw(偏航角)。如此三个维度的旋转矩阵分别是：

而R=RxRyRz：

旋转之后的激光雷达坐标系与相机坐标系同向，但是坐标原点的位置并没有变，所以还要再加上一个平移T。这里的旋转矩阵和平移向量的求解即我们要做的由激光雷达到相机的外参标定。怎么标呢?网上提供了不少的思路。比较常见的比如使用Autoware标定工具,使用solvePnp求解等。这里为了理解标定的具体原理采用手动标定的方式，通过按键移动激光雷达坐标系的位置以及旋转的角度来对齐激光雷达和相机坐标系下的参照物。这种方式虽然存在一定的误差，而且相对比较依赖经验，但是在标定的过程中比较有参与感，对于理解标定原理很有意义。

【参考文献】

https://blog.csdn.net/floatinglong/article/details/116175325

https://blog.csdn.net/learning_tortosie/article/details/82347694 #激光雷达和相机的联合标定

https://blog.csdn.net/qq_29462849/article/details/88748028#commentBox #激光雷达和相机的联合标定的实现

https://blog.csdn.net/fireflychh/article/details/82352710 #坐标轴旋转

https://d3cw3dd2w32x2b.cloudfront.net/wp-content/uploads/2012/07/euler-angles1.pdf #计算欧拉角