高阶数据结构学习 —— 图（2）

---

1、BFS

广度优先。确定从哪个点开始，然后用队列来完成遍历。拿出一个点就把和这个点相连的其它点放进去，但是这样前面放进过队列的也有可能被再次放入，所以需要做好标记。一个队列，一个标记容器。在邻接矩阵里写。

		void BFS(const V& src)
		{
			size_t srci = GetVertexIndex(src);
			//队列和标记数组
			queue<int> q;
			vector<bool> visited(_vertexs.size(), false);
			q.push(srci);
			visited[srci] = true;
			size_t n = _vertexs.size();
			while (!q.empty())
			{
				int front = q.front();
				q.pop();
				cout << front << ":" << _vertexs[front] << endl;
				//把front点的邻接顶点放进队列
				for (size_t i = 0; i < n; ++i)
				{
					if (_matrix[front][i] != MAX_W && !visited[i])
					{
						q.push(i);
						visited[i] = true;
					}
				}
			}
			cout << endl;
		}

测试代码

	void TestGraphBDFS()
	{
		string a[] = { "张三", "李四", "王五", "赵六", "周七" };
		Graph<string, int> g1(a, sizeof(a) / sizeof(string));
		g1.AddEdge("张三", "李四", 100);
		g1.AddEdge("张三", "王五", 200);
		g1.AddEdge("王五", "赵六", 30);
		g1.AddEdge("王五", "周七", 30);
		g1.BFS("张三");
	}

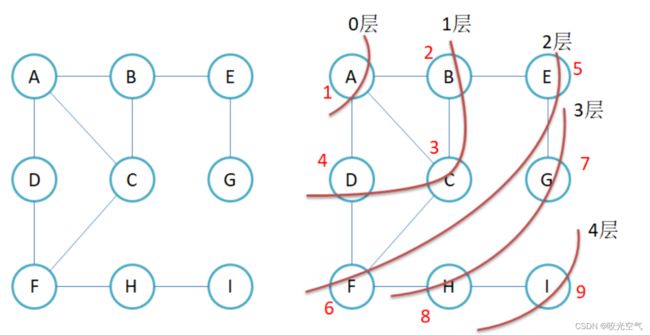
我们加入别的功能，现在要记录走了几层。比如对于A来说，连接B，B连接C，B是A的第一层节点，C是A的第二层节点。

		void BFS(const V& src)
		{
			size_t srci = GetVertexIndex(src);
			//队列和标记数组
			queue<int> q;
			vector<bool> visited(_vertexs.size(), false);
			q.push(srci);
			visited[srci] = true;
			int levelSize = 1;
			size_t n = _vertexs.size();
			while (!q.empty())
			{
				for (int i = 0; i < levelSize; ++i)
				{
					int front = q.front();
					q.pop();
					cout << front << ":" << _vertexs[front] << " ";
					//把front点的邻接顶点放进队列
					for (size_t i = 0; i < n; ++i)
					{
						if (_matrix[front][i] != MAX_W && !visited[i])
						{
							q.push(i);
							visited[i] = true;
						}
					} 
				}
			}
			cout << endl;
			levelSize = q.size();
		}

测试代码

	void TestGraphFS()
	{
		string a[] = { "张三", "李四", "王五", "赵六", "周七" };
		Graph<string, int> g1(a, sizeof(a) / sizeof(string));
		g1.AddEdge("张三", "李四", 100);
		g1.AddEdge("张三", "王五", 200);
		g1.AddEdge("王五", "赵六", 30);
		g1.AddEdge("王五", "周七", 30);
		g1.BFS("张三");
	}

1、DFS

深度优先。

不是从起始点开始走，从连接起始点的一个点开始走，上图的顺序就是A，BCFD，D不能到A，就返回到F，F还有边没走，于是HI，然后I没有可走的，回到H，H也没有可走的了，一直回到B，B还有E可走，然后BEG，再从G返回到。深度的话就是走递归，但因为是图，比较复杂，层数多的话就不要深度了。

		void _DFS(size_t srci, vector<bool>& visited)
		{
			cout << srci << ":" << _vertexs[srci] << endl;
			visited[srci] = true;
			//找一个srci相邻的没有访问过的点
			for (size_t i = 0; i < _vertexs.size(); ++i)
			{
				if (_matrix[srci][i] != MAX_W && visited[i] == false)
				{
					_DFS(i, visited);
				}
			}
		}

		void DFS(const V& src)
		{
			size_t srci = GetVertexIndex(src);
			vector<bool> visited(_vertexs.size(), false);
			_DFS(srci, visited);
		}

测试代码

	void TestGraphFS()
	{
		string a[] = { "张三", "李四", "王五", "赵六", "周七" };
		Graph<string, int> g1(a, sizeof(a) / sizeof(string));
		g1.AddEdge("张三", "李四", 100);
		g1.AddEdge("张三", "王五", 200);
		g1.AddEdge("王五", "赵六", 30);
		g1.AddEdge("王五", "周七", 30);
		g1.DFS("张三");
	}

用邻接矩阵的话，如果是稠密图还好，稀疏图就得循环更多没有值的地方。

---

如果图不是连通图，那么两个搜索其实都会受影响，会出现到了某个位置遍历断掉了。如何保证遍历所有的顶点？解决办法就是遍历一次后，再找后面有false的点，以这个点作为起点再次开始循环，就可以了。

本篇gitee

下一篇写最小生成树问题。

结束。