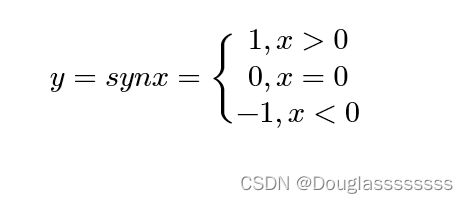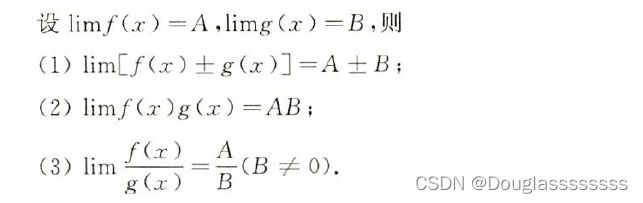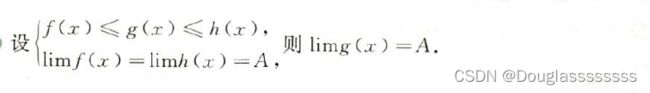【考研数学】高等数学第一模块——函数、极限、连续
目录
- 前言
- 基本概念
-
- 一、函数
-
- 性质
- 复合函数
- 反函数
- 初等函数
- 特殊函数
- 二、极限
-
- 定义
- 一般性质
- 运算性质
- 存在性质
- 无穷小量
- 两个重要极限
- 三、连续与间断
-
- 概念
- 闭区间上性质
- 题型思路
-
- 关于极限的概念性质
- 极限的计算
- 写在最后
前言
写这一类的文章,还是比较吃力不讨好的。一是已经有非常多优秀的博主在写了,质量都很高。另一是很多数学公式要表达,比较费时间。还有就是本身我是非数学类的,有很多的理解都只是浅显的。因此希望大家见谅,有任何不规范的地方,都欢迎大家指正。
我考的是数一,内容很多,有点担心会影响自己的复习进度。写这一系列文章,主要是帮自己巩固一遍,希望能坚持下去。
我跟着的是汤神,比较喜欢。老汤说要“通俗而又深刻”,希望自己也能往这方面靠。
基本概念
其实这一部分的概念应该大家都再熟悉不过了,但是也正是这样,很多人都忽视掉了。静下来再好好看看一些相关的定义和定理,相信能让基础更加扎实些。
一、函数
定义:设 x , y x,y x,y 是两个变量, D D D是一个给定的非空数集,如果对于每个数 x ∈ D x \in D x∈D,按照某个对应法则 f f f,变量 y y y 都有唯一确定的数值和它对应,则称变量 y y y 是变量 x x x的函数。
可以说有了函数,一个数集就可以映射到另一个数集。
性质
- 有界性:设 y = f ( x ) ( x ∈ D ) y=f(x)(x \in D) y=f(x)(x∈D),若存在 M > 0 M>0 M>0,对任意的 x ∈ D x \in D x∈D,总有 ∣ f ( x ) ∣ ≤ M |f(x)| \leq M ∣f(x)∣≤M,称函数 f ( x ) f(x) f(x) 在D上有界。
注意,有一个绝对值,同时有上下界才叫有界。
- 单调性:设 y = f ( x ) y=f(x) y=f(x) 在区间 I I I 上有定义,如果 ∀ x 1 , x 2 ∈ I \forall x_1,x_2\in I ∀x1,x2∈I,当 x 1 < x 2 x_1 < x_2 x1<x2 时,恒有 f ( x 1 ) ≤ f ( x 2 ) f(x_1) \leq f(x_2) f(x1)≤f(x2) 或 f ( x 1 ) ≥ f ( x 2 ) f(x_1) \geq f(x_2) f(x1)≥f(x2) ,则称 y = f ( x ) y=f(x) y=f(x) 在区间 I I I 上单调递增(单调递减)。
大于等于号不是严格的,把等号去掉是严格递增。
- 周期性: ∃ T \exist T ∃T( T T T 为常数,且 T ≠ 0 T \neq 0 T=0,有 f ( x ± T ) = f ( x ) f(x \pm T)=f(x) f(x±T)=f(x),称 f ( x ) f(x) f(x) 为周期函数,最小正数 T T T为 f ( x ) f(x) f(x)的周期。
注意下最小正周期,也就是说如果找不到最小的,那就没有周期。比如后面要说的狄利克雷函数就没有周期,常数函数也没有周期。
- 奇偶性:这个就不详细说了,大家高中就学过,用的也多。
复合函数
这里主要说一下,怎么求复合函数的定义域的问题。
- 已知 f ( x ) f(x) f(x)的定义域为 [ a , b ] [a,b] [a,b],求 f [ g ( x ) ] f_{[g(x)]} f[g(x)]的定义域。则令 g ( x ) ∈ [ a , b ] g(x) \in [a,b] g(x)∈[a,b]即可求得。
- 已知 f [ g ( x ) ] f_[g(x)] f[g(x)]定义域为 [ a , b ] [a,b] [a,b],求 f ( x ) f(x) f(x)的定义域,则应计算 g ( x ) g(x) g(x)在 [ a , b ] [a,b] [a,b]上的值域,即为 f ( x ) f(x) f(x)的定义域。
反函数
高中我们把x和y换位置,写成 y = f ( x ) y=f(x) y=f(x)的样子,比如 y = 2 x y=2x y=2x的反函数是 y = 1 2 x y=\frac{1}{2}x y=21x。但现在我们不能把他们调换位置, y = 2 x y=2x y=2x的反函数就是 x = 1 2 y x=\frac{1}{2}y x=21y ,记为 x = f − 1 ( y ) x=f^{-1}(y) x=f−1(y) 。
反函数的定义域即原函数的值域,反函数的值域即原函数的定义域。
反函数和原函数的复合函数为 x x x 。设原函数为 y = f ( x ) y=f(x) y=f(x) ,则反函数为 x = f − 1 ( y ) x=f^{-1}(y) x=f−1(y) 。那么有 f − 1 ( f ( x ) ) = f − 1 ( y ) = x f^{-1}(f(x))=f^{-1}(y)=x f−1(f(x))=f−1(y)=x 。
注意,原函数在定义域内严格单调才有反函数,比如 y = x 2 y=x^2 y=x2就没有反函数。
初等函数
初等函数是由基本初等函数经过有限次的有理运算(加、减、乘、除、有限次乘方、有限次开方)及有限次函数复合所产生。基本初等函数包括幂函数、指数函数、对数函数和三角函数。
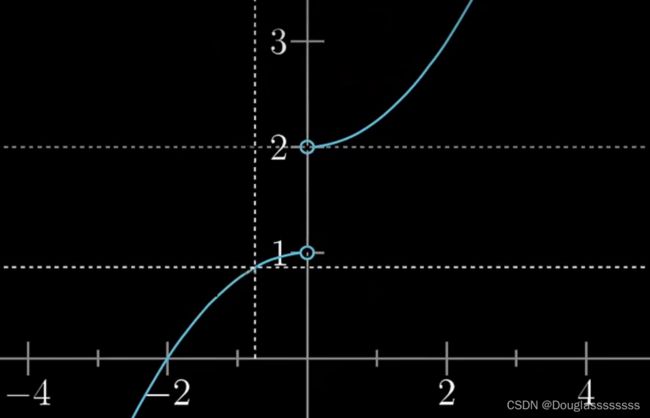
这些函数的图像需要去知道大概是什么样的,我们经常忘记的可能就是一些三角函数。
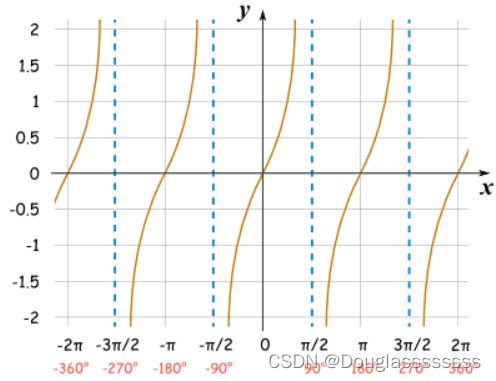
正切函数(上图), π 2 \frac{\pi}{2} 2π是渐近线。
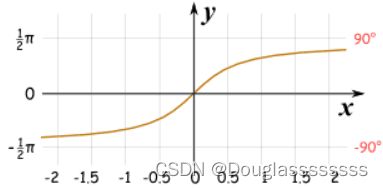
反正切( x ∈ R , y ∈ ( − π 2 , π 2 ) x \in R,y \in (-\frac{\pi}{2},\frac{\pi}{2}) x∈R,y∈(−2π,2π))。注意 π 2 \frac{\pi}{2} 2π是取不到的,可以和下图的反正弦对比一下。
反正弦( x ∈ [ − 1 , 1 ] , y ∈ [ − π 2 , π 2 ] x \in [-1,1],y \in [-\frac{\pi}{2},\frac{\pi}{2}] x∈[−1,1],y∈[−2π,2π])
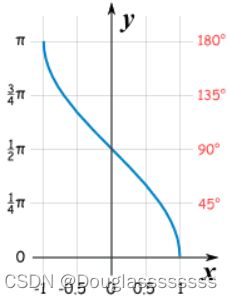
反余弦( x ∈ [ − 1 , 1 ] , y ∈ [ − π , π ] x \in [-1,1],y \in [-\pi,\pi] x∈[−1,1],y∈[−π,π])
特殊函数
这个狄利克雷函数有点像bug,好像存在就是为了推翻某些绝对的特例,就比如说它处处间断。很多时候某个结论不确定,可以考虑它,或者这种取有理数无理数的,不一定是取1,0。
取整函数: y = [ x ] y=[x] y=[x]
这个有点恶心的函数,我们需要记住一个不等式 x − 1 ≤ [ x ] ≤ x x-1 \leq [x] \leq x x−1≤[x]≤x。
二、极限
定义
- 数列极限:若对任意的 ϵ > 0 , ∃ N > 0 \epsilon > 0 , \exist N>0 ϵ>0,∃N>0,当 n > N n>N n>N时,有 ∣ a n − A ∣ < ϵ |a_n -A|< \epsilon ∣an−A∣<ϵ称 A A A为数列{ a n a_n an}的极限,记为: lim n → ∞ a n = A \lim_{n \to \infty} a_n=A n→∞liman=A
- 函数极限(趋于某点): ∀ ϵ > 0 , ∃ δ > 0 \forall \epsilon>0,\exist \delta>0 ∀ϵ>0,∃δ>0,当 0 < ∣ x − a ∣ < δ 0<|x-a|<\delta 0<∣x−a∣<δ时,有 ∣ f ( x ) − A ∣ < ϵ |f(x)-A|<\epsilon ∣f(x)−A∣<ϵ,称 A A A为 f ( x ) f(x) f(x)当 x → a x\to a x→a时的极限,记为: lim x → a f ( x ) = A \lim_{x\to a}f(x)=A x→alimf(x)=A
函数极限还有趋于无穷的情况我就不详细说了。
其实定义对于求一些极限是发挥不上作用的,常用于一些证明题,很管用。但是由于晦涩的数学表达,缺乏直观感受,就算让我们知道要用定义,也还是下不了手。
因此我认为应该首先真正弄明白这样数学表达的直观感受,不会对它产生恐惧心理。可以去看看3B1B的一些视频。
拿函数区域某点的极限为例,可以直观上理解为:当x从某一个数附近向该值靠拢时,对应的y也从某一个数附近向一个值靠拢。
如果x在向某一点靠拢时,y并没有趋于某一个值,那极限就不存在。
函数的极限后面用的也多,数列极限倒是让人很头疼,我这里就写一个用数列极限定义证明的例题吧,帮助大家理解。其实就是找到一个N,满足极限定义的条件即可。中括号是向下取整的意思。
一般性质
数列极限和函数极限的性质有点子不一样哈,需要注意。
- 唯一性:极限存在即唯一。
这个性质两者相同,这个大家都知道。
这里需要特别说明,数列极限是整个定义域内都有界,而函数极限是叫作局部有界,也就是在那个 δ \delta δ去心邻域内才有界。证明过程还算巧妙,可以去了解了解。
- 保号性:设 lim x → a f ( x ) = A > 0 \lim_{x \to a}f(x)=A>0 x→alimf(x)=A>0则 ∃ δ > 0 \exists \delta>0 ∃δ>0,当 0 < ∣ x − a ∣ < δ 0<|x-a|<\delta 0<∣x−a∣<δ时,有 f ( x ) > 0 f(x)>0 f(x)>0.
和有界性一样,数列是保号性,而函数极限是局部保号。
老汤讲啦,这个非常重要,虽然我不是很觉得哈哈哈哈。这块我就写详细些。
首先是证明过程:
不妨设 A > 0 A>0 A>0,取 ϵ = A 2 > 0 \epsilon=\frac{A}{2}>0 ϵ=2A>0,有极限等于A,根据定义, ∃ δ > 0 \exists \delta >0 ∃δ>0,当 0 < ∣ x − a ∣ < δ 0<|x-a|<\delta 0<∣x−a∣<δ时, ∣ f ( x ) − A ∣ < A 2 → − A 2 < f ( x ) − A < A 2 , |f(x)-A|<\frac{A}{2}\to -\frac{A}{2}
其实就是取了 ϵ = A 2 \epsilon=\frac{A}{2} ϵ=2A,按照定义推了一遍。
其次是一些推论:
也就是函数正负同样可以推得极限正负,函数不负,极限不负,函数不正,极限不正。
但是若函数条件仅为 f ( x ) > 0 f(x)>0 f(x)>0,无法得到极限也大于0。因为对于 x → ∞ x\to \infty x→∞的极限,即使函数或数列通项大于0,极限也可能等于0.如 f ( x ) = 1 x 2 + 1 , a n = 2 − n . f(x)= {1\over x^2+1},a_n=2^{-n}. f(x)=x2+11,an=2−n.
综上,对于自变量趋于某点的极限,保号性没什么限制,可以自由去极限和互相推出。但是对于自变量趋于无穷的函数极限和数列极限,即使函数或通项大于0,极限也可能为0。因此解题时需对极限为0进行判断取舍。
这个碰到的少,对于x型的极限,考虑子列,对于n型的极限,则考虑列。
补充一点就是,如果子列凑起来是完整的列,也可以说明列极限存在。如奇子列和偶子列极限都存在且相等,可以说明原极限存在。
运算性质
这个没有什么多说的,注意能运算的前提是两个极限都存在,才可以拆开或合并。
存在性质
这个大家应该用的很多了,尤其是对于求一些数列极限,我这里补充一下证明过程,可以看一看,扩展思路。
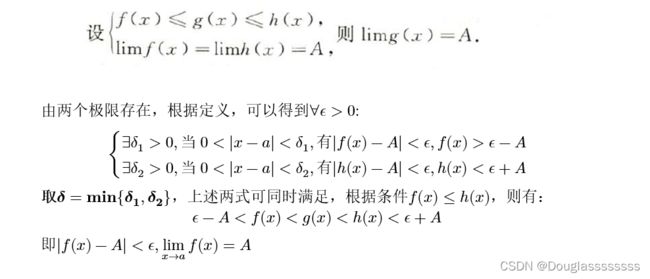
这样取两者大或小的思想在保号性证明里也用了。
补充一个常用的结论: a , b , c > 0 , lim n → ∞ ( a n + b n + c n ) 1 n = m a x ( a , b , c ) a,b,c>0, \lim_{n\to \infty}(a^n+b^n+c^n)^{\frac{1}{n}}=max(a,b,c) a,b,c>0,n→∞lim(an+bn+cn)n1=max(a,b,c)
2.数列单调有界收敛准则
这个最常见的题型就是让你根据一个递推关系或者其他条件,证明一个数列极限存在,然后让你求它。一般难的是前者,后者只要两边同时取极限很好求,有的时候前面实在证明不出,可以先求出极限反推一下。
我这里就说说单调性的一些常见证明方法吧。
- 作差法
- 基本不等式
这里顺带提一下这个基本不等式,个人感觉很基础,但是又不能忽视。
常用不等式如下:
- ∣ ∣ a ∣ − ∣ b ∣ ∣ ≤ ∣ a ± b ∣ ≤ ∣ a ∣ + ∣ b ∣ ||a|-|b||\leq|a\pm b|\leq|a|+|b| ∣∣a∣−∣b∣∣≤∣a±b∣≤∣a∣+∣b∣
- s i n x ≤ x ≤ t a n x , x ∈ [ 0 , π 2 ) sinx\leq x\leq tanx,x\in[0,\frac{\pi}{2}) sinx≤x≤tanx,x∈[0,2π)
- e x ≥ x + 1 e^x\geq x+1 ex≥x+1
- 调和平均值<=几何平均值<=算术平均值<=方均根
- 归纳法
这个是高中基础了,三步走,可以自己总结一下模板。
- 拉格朗日定理
这个严格来说也算作差法,反正看到两个函数值的差,下意识就要去想拉格朗日,这个太重要啦。
无穷小量
这个我也不多提,用的太多啦,不过提醒一下别忘了K阶无穷小是什么意思。还有就是无穷小的运算法则,有时候用泰勒的时候能用上。
t × ο ( t ) = ο ( t 2 ) , ο ( t 2 ) + ο ( t 3 ) = ο ( t 2 ) t\times\omicron(t)=\omicron(t^2),\omicron(t^2)+\omicron(t^3)=\omicron(t^2) t×ο(t)=ο(t2),ο(t2)+ο(t3)=ο(t2) ο ( t 2 ) × ο ( t 3 ) = ο ( t 5 ) , ο ( t 2 ) × 3 = ο ( t 2 ) \omicron(t^2) \times \omicron(t^3)=\omicron(t^5),\omicron(t^2)\times3=\omicron(t^2) ο(t2)×ο(t3)=ο(t5),ο(t2)×3=ο(t2)
两个重要极限
用的也很多,我要补充的是第二个极限,括号里要是(1+无穷小)的形式。
三、连续与间断
概念
连续是针对某点的性质,函数在某点处连续,在这点的邻域内都不一定连续。比如说下面这个狄利克雷形式的函数: y = { 0 x 为有理数 x 2 x 为无理数 y=\begin{cases} 0 & x为有理数 \\ x^2 & x为无理数 \\ \end{cases} y={0x2x为有理数x为无理数
- 在区间连续:两个条件,一是在开区间处处连续,这个只要有定义就能做到。二是左端点右连续,右端点左连续。可记作 f ( x ) ∈ C [ a , b ] f(x)\in C[a,b] f(x)∈C[a,b],C是 " C o n t i n u o u s " "Continuous" "Continuous".
- 间断点分类:

注意,前提是函数值不等于左右极限值,不然就连续了。
闭区间上性质
这个很重要,在证明题里经常能用上,需要注意的是这些性质的条件一定是在闭区间上连续的。
题型思路
有了上面这些基础打底后,再做一些习题去加强记忆和理解,最后不会的听汤老师讲解,效果好的一塌糊涂啊。
关于极限的概念性质
这种选择题见的多,给一个极限存在或者其他条件,判断各个选项正确与否。我个人感觉比较难,要现场去证明做不到,大多是举反例和凭感觉。
比如下面这个题,我觉得我肯定想不到举这些例子。
极限的计算
对于数列极限计算,常用的思路有:
- 夹挤定理(常配合放缩)
- 转为函数极限(令 x = 1 n x= {1\over n} x=n1)
- 用裂项公式,求和就剩首尾两项
- 定积分定义
对于函数极限计算,常用的思路有:
- 无穷小替换
- 洛必达法则
- 泰勒展开
- 拉格朗日中值定理(出现同形式函数值作差时)
- 取对数
- x → ∞ x\to \infty x→∞时化为分母形式或令 t = 1 x t={1 \over x} t=x1
- 三角函数替换
- 提取公因式凑1,方便利用无穷小替换
对于指数函数如 e x e^x ex和根号函数,趋于无穷时要考虑下正负无穷。
写在最后
要想比较完整的包含极限这一部分的所有内容,是比较困的。题目类型有很多,需要大量的练习。不过这些练习都是值得的,因为后面的内容,很多都是在极限的基础上进行的。
文章主要起查漏补缺的作用吧,希望能 H e l p f u l . Helpful. Helpful.