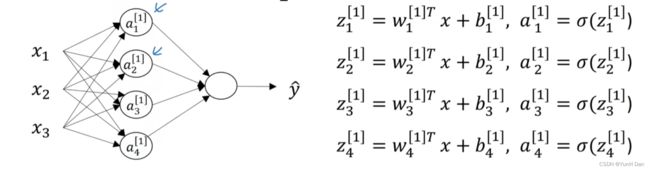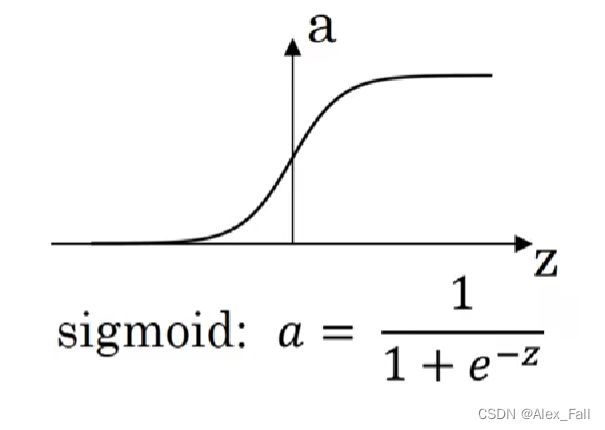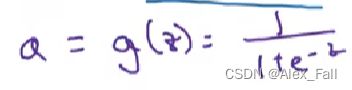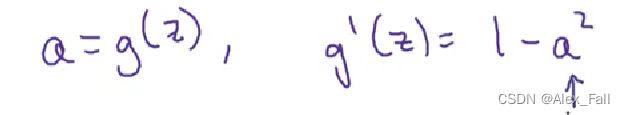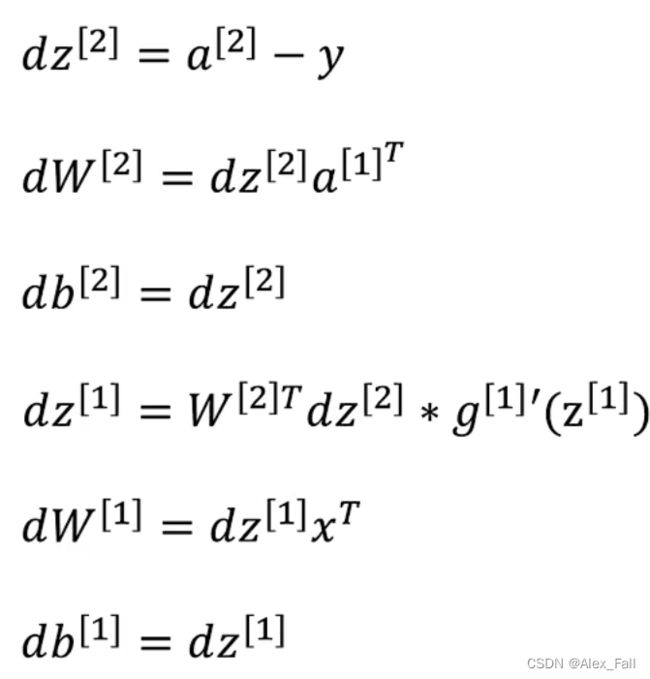单隐层神经网络

这是单隐层神经网络的一些知识，那么话不多说，开始学习~

单隐层神经网络与Logistic回归：

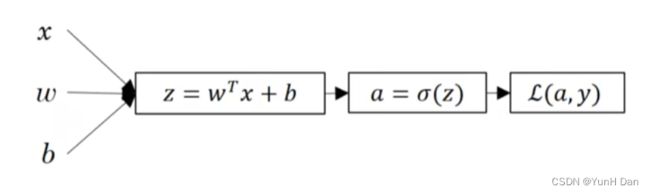
        让我们来回顾一下Logistic回归的流程图：

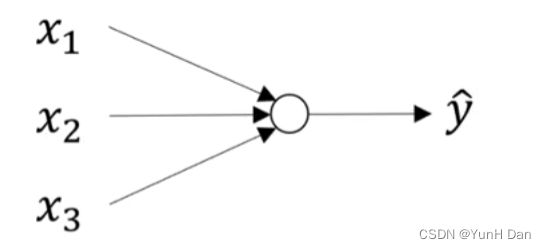
这是样本集的一次Logistic回归计算，这其实可以被抽象为一个神经元接收样本集x，然后输出预测集y帽的过程：

 但是对于这样的一次样本集迭代，我们完全可以一次性执行多次Logistic回归计算。通过将多个这样的神经元堆叠起来，然后用一个输出神经元来接收这些神经元的结果作为输入x，又进行一次Logistic回归计算，然后输出最终结果，我们就建立了一个单隐层的神经网络：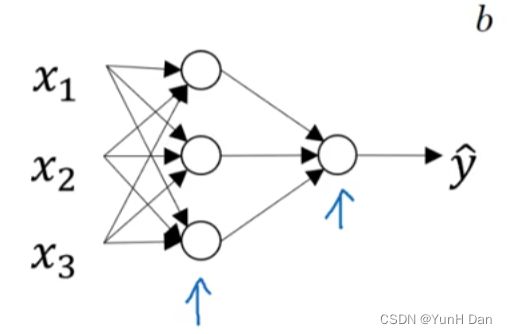

         事实上，隐层可以堆叠任意个神经元，一般而言，堆叠个数越多，学习的效率越高。

        我们其实观察可以发现，单隐层神经网络实际上是一个双层神经网络，所以，通过类比推测，我们可以知道，如果有n个隐层，总层数就是n+1，+1是加上了最后的输出层。通过第二周的笔记我们知道，输入层是不被考虑在层数内的。

一个神经元在干什么？：

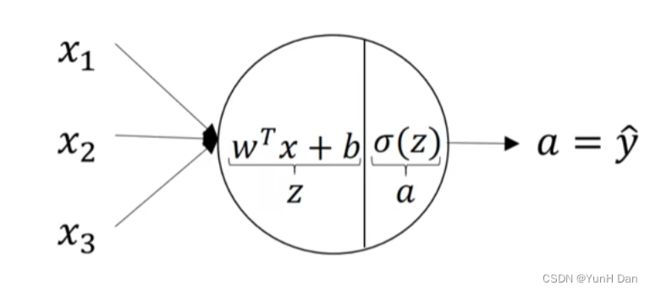
我们知道一个神经元在计算一次Logistic回归计算，我们来深入看一下其内部细节：

 输入进来的样本x，首先会运用wT·x+b计算出缓存z，然后通过激活函数sigmoid得到激活值a，这个激活值a也就是最后的输出y帽。所以，一个神经元进行了两个步骤。

符号约定：

1.通常，我们用上标方括号来表示第几层，比如x1，x2，x3那一列，一般设为第0层，也就是[1]，然后，第一个隐层，就是[1]，只有一个神经元的输出层是[2]。

2.然后，上标用圆括号表示第几个样本，如果对这个单隐层神经网络输入第一个样本，那么就是(1)，第二个样本为(2)，以此类推，第i个样本被称为(i)。

3.用下标i表示该层内第i个神经元。

确保弄懂了这些符号，示例：

 向量化单隐层神经网络：

        我们可以看到，在代码实现的时候，如果要用4次for循环，每次for循环代表一个神经元对一个样本集的迭代计算，那么效率会非常的低，同样，我们可以考虑使用向量化，将隐层的所有z，a，w，b堆叠起来，形成矩阵：Z， A， W， b。事实证明，他们都可以被看作是行向量形式的分块矩阵：

        

 以Z为例，z1，z2，z3，z4都是列向量，向量的元素个数与输入样本：向量x的元素个数相同，也就是说，如果x是3*1的向量，那么z1，z2，z3，z4也是3*1的向量，W，A，b也是如此。

不得不说明一下，由于每次Logistic回归计算的b是一个实数，因此一个隐层堆叠起来后，得到的b实际上只是一个向量，如果隐层有n个神经元，那么b就是n*1维。计算Z如下：

 不难发现，我们是将W进行转置后与x进行矩阵乘法的，每个列向量w都变成了行向量wT。这里是一个样本的情况，所以最后得到的矩阵Z实际上列数只有1列，这时候Z对应上面的行向量形式其实就是[z1]。如果有三个样本，那么Z毋庸置疑为[z1 z2 z3]，分别为对每个样本计算得到的缓存z。

        这样就得到了向量化版本的单隐层神经网络，而且是一个样本的情况：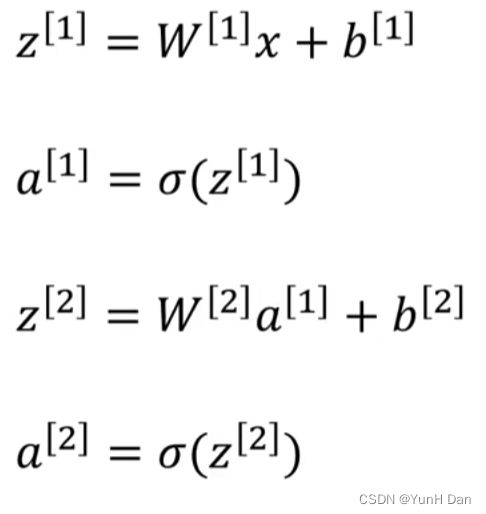

 这里z没有大写没有关系。但是，留心发现，W与x矩阵乘法没有转置，这是因为大写的W实际上是对原w矩阵进行转置得到的矩阵W，也就是wT = W。

通过自己的手动推导，a[1]实际上是一个行向量形式的矩阵。而由于输出层只是一个神经元，因此，在计算W与a[1]时，为保证矩阵乘法的合法性，将输出层神经元的w直接与a[1]进行矩阵乘法。如果输出层不是只有一个神经元，那么操作同隐层，将w矩阵事先转置为W，然后与a[1]进行矩阵乘法。

        附上自己的推导过程，这里是一个样本集的情况，有三个样本，每个样本维数为2*1，而且隐层的隐藏神经单元个数为3个：

（感觉貌似是给我看的hhh，当然还是自己推导一遍比较好）

激活函数的选择：

从Z到A，实际上经过了一次激活，比如用sigmoid计算A，就是把Z激活成A的过程。其实激活函数不只是sigmoid，还有双曲正切函数tanh，修正线性单元ReLU——绪论有提到。那么它们什么时候用呢？

sigmoid函数：

函数曲线和表达式如下：

 我们可以观察到，sigmoid的值域在0-1之间，所以对反应概率方面十分合适。但是它有个弊病，就是不能取到负数，这无助于将数据平均于0，也就是对数据中心化无帮助。因此sigmoid常常只用在以概率作为区分方法的二分分类神经网络的输出层里。

导数为：

                        

tanh双曲正切函数：

函数曲线和表达式如下：

导数为：

 在数学上，tanh实际是sigmoid函数向下平移后得到的结果，也就是其值域是（-1， 1）。因此，它可以将数据中心化，提高神经网络的效率。所以它常常用在单隐层神经网络里。

ReLU修正线性单元：

函数曲线和表达式如下：

导数为：

 从函数表达式看出，函数值是0和自变量z之间取最大值，所以可以看到，在z为负数时，函数值为0，在z为非负数时，函数值呈正比增长，看出其导数永远不变，为一恒定值，因此在学习的过程中，常常能保持学习效率，所以常被用在深层的神经网络里以保证学习效率。

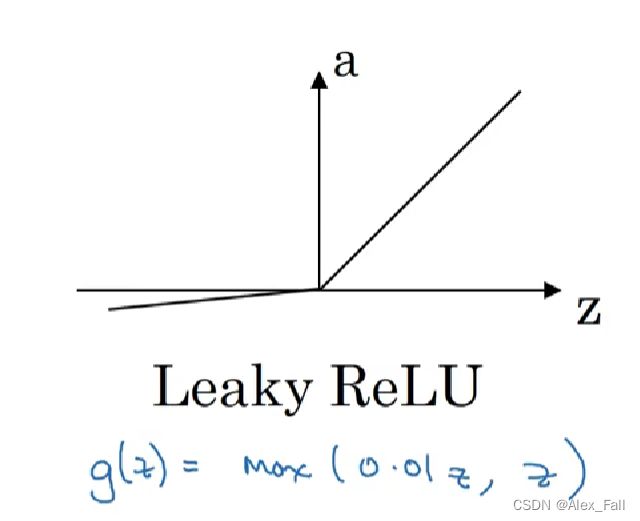
带缺陷的修正线性单元ReLU：

 导数为：

 有时候这个函数作为激活函数会发挥挺不错的作用。

为什么选择非线性激活函数？

假设我们在隐藏层内使用呈线性正比的函数（统称为线性函数），在输出层依旧保持sigmoid函数，那么会发生什么？最简单的例子，假设激活函数就是y = x，那么隐藏层就有：A1 = Z1 = W1.T·X + b1，在输出层再一次出现：A2 = sigmoid（Z2） = sigmoid（W2.T·A1 + b2）= sigmoid【W2.T · （W1.T · X + b1） + b2】 = sigmoid（W2.T · W1.T · X + W2.T · b1 + b2）

假如把W2.T·W1.T 看作一个整体：W*， 把W2.T · b1 + b2看作一个整体：b*，那么A2 = sigmoid（Z2） = sigmoid（W* ·X + b*），这说明了什么？

如果这不是一个单隐层的神经网络，而是深层的神经网络，那么可以想象，我们经过多次的隐层之后，最终得到的还是类似上面形式的结果，那么我们还不如不设置这么深层的网络，直接提前用W1， W2......Wn和b1， b2......bn计算好W*和b*，然后用一个神经元就可以解决了。

这就说明，如果激活函数是线性的，那么神经网络的隐藏层就相当于摆设，发挥不了作用，因此我们才需要非线性激活函数。

反向传播中的导数公式：

推导可以自行推导，比较简单。

随机初始化：

先上结论：一般对W进行随机初始化，而偏向量b一般可以设置为0。

也就是说在隐层里面有若干个单元，我们要让这些单元的w向量都不相同，如果相同的话，那么其实这个隐层这么多单元，都将会被看成一个单元，因为权重w才是更重要的。保证了权重的不同，就保证了函数式的不同，也就保证了每个单元的z是不一样的。

让w都相同的初始化被称为完全对称，在深层神经网络中，该层神经元的w都相同将会导致下一层也出现完全对称，使得下一层的输入x向量的每个元素都是相同的，那么如果下一层的w也是相同的，那么下一层的输出z又是相同的了！这样反反复复，既然每一层的每个单元的输出都是相同的，那么为什么每一层还要设置那么多神经元呢？直接每一层一个神经元不就可以了吗？

所以这就是为什么要随机初始化的原因。