Go-Python-Java-C-LeetCode高分解法-第十二周合集

前言

本题解Go语言部分基于 LeetCode-Go
其他部分基于本人实践学习
个人题解GitHub连接：LeetCode-Go-Python-Java-C
欢迎订阅CSDN专栏，每日一题，和博主一起进步
LeetCode专栏
我搜集到了50道精选题，适合速成概览大部分常用算法
突破算法迷宫：精选50道-算法刷题指南

文章目录

前言
[78. Subsets](https://leetcode.com/problems/subsets/)
- 题目
- 题目大意
- 解题思路
- 代码
- Go
- Python
- Java
- Cpp
[79. Word Search](https://leetcode.com/problems/word-search/)
- 题目
- 题目大意
- 解题思路
- 代码
- Go
- Python
- Java
- Cpp
[80. Remove Duplicates from Sorted Array II](https://leetcode.com/problems/remove-duplicates-from-sorted-array-ii/)
- 题目
- 题目大意
- 解题思路
- 代码
- Go
- Python
- Java
- Cpp
[81. Search in Rotated Sorted Array II](https://leetcode.com/problems/search-in-rotated-sorted-array-ii/)
- 题目
- 题目大意
- 解题思路
- 代码
- Go
- Python
- Java
- Cpp
[82. Remove Duplicates from Sorted List II](https://leetcode.com/problems/remove-duplicates-from-sorted-list-ii/)
- 题目
- 题目大意
- 解题思路
- 代码
- Go
- Python
- Java
- Cpp
[83. Remove Duplicates from Sorted List](https://leetcode.com/problems/remove-duplicates-from-sorted-list/)
- 题目
- 题目大意
- 解题思路
- 代码
- Go
- Python
- Java
- Cpp
[84. Largest Rectangle in Histogram](https://leetcode.com/problems/largest-rectangle-in-histogram/)
- 题目
- 题目大意
- 解题思路
- 代码
- Go
- Python
- Java
- Cpp

78. Subsets

题目

Given a set of distinct integers, nums, return all possible subsets (the power set).

Note: The solution set must not contain duplicate subsets.

Example:

Input: nums = [1,2,3]
Output:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

题目大意

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。说明：解集不能包含重复的子集。

解题思路

找出一个集合中的所有子集，空集也算是子集。且数组中的数字不会出现重复。用 DFS 暴力枚举即可。
这一题和第 90 题，第 491 题类似，可以一起解答和复习。
让我们分别介绍每个版本的解题思路：

Go 版本：

subsets 函数初始化一个空切片 c 用于存储当前生成的子集，以及一个空切片 res 用于存储最终的结果。
使用一个循环来遍历不同大小的子集，从空集合开始到包含所有元素的集合。
在每个循环中，调用 generateSubsets 函数来生成当前大小 k 的子集，并将其添加到 res 中。
generateSubsets 函数是一个递归函数，用于生成指定大小 k 的子集。它从 start 索引开始，依次将元素添加到 c 中，然后递归生成子集。
当 c 中的元素数量达到 k 时，表示一个子集生成完成，将其添加到 res 中。
在 generateSubsets 函数中，使用回溯操作来移除最后一个元素，以便尝试下一个元素。

Python 版本：

与 Go 版本类似，Python 版本使用递归和循环来生成子集。
subsets 函数初始化一个空列表 res 用于存储最终的结果。
使用一个循环来遍历不同大小的子集，从空集合开始到包含所有元素的集合。
在每个循环中，调用 generateSubsets 函数来生成当前大小 k 的子集，并将其添加到 res 中。
generateSubsets 函数是一个递归函数，用于生成指定大小 k 的子集。它从 start 索引开始，依次将元素添加到 c 中，然后递归生成子集。
当 c 中的元素数量达到 k 时，表示一个子集生成完成，将其添加到 res 中。
在 generateSubsets 函数中，使用回溯操作来移除最后一个元素，以便尝试下一个元素。

Java 版本：

Java 版本同样使用递归和回溯来生成子集。
subsets 函数初始化一个空的 ArrayList 对象 res 用于存储最终的结果。
在 subsets 函数中，调用辅助函数 generateSubsets 来生成子集。
generateSubsets 函数是一个递归函数，用于生成子集。它将当前子集 subset 加入到 res 中，然后从 start 索引开始逐个添加元素，递归生成子集。
当 subset 达到目标大小时，将其加入到 res 中，然后进行回溯操作，移除最后一个元素，以便尝试下一个元素。

C++ 版本：

C++ 版本与其他版本类似，使用递归和回溯来生成子集。
subsets 函数初始化一个空的向量 res 用于存储最终的结果。
在 subsets 函数中，调用辅助函数 generateSubsets 来生成子集。
generateSubsets 函数是一个递归函数，用于生成子集。它将当前子集 subset 加入到 res 中，然后从 start 索引开始逐个添加元素，递归生成子集。
当 subset 达到目标大小时，将其加入到 res 中，然后进行回溯操作，移除最后一个元素，以便尝试下一个元素。

总的来说，不论使用哪种编程语言，解题思路都是使用递归和回溯技术来生成不同大小的子集，然后将这些子集添加到结果集中。递归的基本思想是生成一个子集，然后递归生成下一个子集，直到达到目标大小。回溯操作用于维护和移除生成子集的元素，以便尝试其他可能性。这种方法能够生成所有可能的子集，包括空集。

代码

Go

// 定义一个函数 subsets，它接受一个整数数组 nums，返回这个数组的所有子集。
func subsets(nums []int) [][]int {
    // c 用于暂时存储正在生成的子集，res 用于存储所有生成的子集。
    c, res := []int{}, [][]int{}
    
    // 通过循环生成不同大小的子集，从空集合到包含全部元素的集合。
    for k := 0; k <= len(nums); k++ {
        // 调用 generateSubsets 函数来生成当前大小 k 的子集，并将其加入 res 中。
        generateSubsets(nums, k, 0, c, &res)
    }
    
    // 返回所有生成的子集。
    return res
}

// 定义一个辅助函数 generateSubsets，用于生成指定大小的子集。
func generateSubsets(nums []int, k, start int, c []int, res *[][]int) {
    // 如果 c 中的元素数量达到了 k，表示一个子集生成完成。
    if len(c) == k {
        // 创建一个新的切片 b，将 c 的内容复制到 b 中，然后将 b 加入到结果集 res 中。
        b := make([]int, len(c))
        copy(b, c)
        *res = append(*res, b)
        return
    }
    
    // 在数组 nums 中，从索引 start 开始，依次将元素加入 c 中，然后递归生成子集。
    // i 最多会到达 len(nums) - (k - len(c)) + 1
    for i := start; i < len(nums) - (k - len(c)) + 1; i++ {
        c = append(c, nums[i]) // 将 nums[i] 加入 c 中
        generateSubsets(nums, k, i+1, c, res) // 递归生成子集，下一轮的起始索引为 i+1
        c = c[:len(c)-1] // 回溯操作，将最后一个元素从 c 中移除，以便尝试下一个元素。
    }
    return
}

Python

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        def generate_subsets(nums, k, start, c, res):
            if len(c) == k:
                res.append(c[:])
                return
            for i in range(start, len(nums) - (k - len(c)) + 1):
                c.append(nums[i])
                generate_subsets(nums, k, i + 1, c, res)
                c.pop()
        
        res = []
        for k in range(len(nums) + 1):
            generate_subsets(nums, k, 0, [], res)
        return res

Java

class Solution {
    public List> subsets(int[] nums) {
        List> res = new ArrayList<>();
        
        // 辅助函数用于递归生成子集
        generateSubsets(nums, 0, new ArrayList(), res);
        
        return res;
    }
    
    private void generateSubsets(int[] nums, int start, List subset, List> res) {
        res.add(new ArrayList<>(subset)); // 将当前子集加入结果集
        
        for (int i = start; i < nums.length; i++) {
            subset.add(nums[i]);
            generateSubsets(nums, i + 1, subset, res); // 递归生成子集，下一轮的起始索引为 i+1
            subset.remove(subset.size() - 1); // 回溯操作，将最后一个元素移除
        }
    }
}

Cpp

class Solution {
public:
    vector> subsets(vector& nums) {
        vector> res;
        vector subset;
        
        // 辅助函数用于递归生成子集
        generateSubsets(nums, 0, subset, res);
        
        return res;
    }
    
    void generateSubsets(vector& nums, int start, vector& subset, vector>& res) {
        res.push_back(subset); // 将当前子集加入结果集
        
        for (int i = start; i < nums.size(); i++) {
            subset.push_back(nums[i]);
            generateSubsets(nums, i + 1, subset, res); // 递归生成子集，下一轮的起始索引为 i+1
            subset.pop_back(); // 回溯操作，将最后一个元素移除
        }
    }
};

理解并解释每个版本的代码需要掌握的基础知识：

Go 版本：
- 切片（Slices）：Go 中的切片是动态数组，用于存储元素的有序集合。在该版本的代码中，切片用于存储当前生成的子集 c 和最终的结果集 res。
- 递归（Recursion）：这个解决方案使用递归来生成子集。理解递归的工作原理和如何处理递归堆栈很重要。
- 循环（Loops）：在 subsets 函数中使用了循环，以便生成不同大小的子集。
Python 版本：
- 递归（Recursion）：与 Go 版本一样，Python 版本也使用递归生成子集。
- 列表（Lists）：Python 中的列表用于存储元素的有序集合，类似于 Go 中的切片。在该版本的代码中，列表用于存储当前生成的子集 c 和最终的结果集 res。
Java 版本：
- 递归（Recursion）：Java 版本使用递归来生成子集。
- 列表（Lists）：Java 中使用 List 接口和 ArrayList 类来表示集合。在该版本的代码中，列表用于存储当前生成的子集 subset 和最终的结果集 res。
- 回溯（Backtracking）：这个解决方案使用回溯技术来处理生成子集的过程。了解如何回溯和维护状态是关键。
C++ 版本：
- 递归（Recursion）：与其他版本一样，C++ 版本也使用递归生成子集。
- 向量（Vectors）：C++ 中的向量（vector）类似于动态数组，用于存储元素的有序集合。在该版本的代码中，向量用于存储当前生成的子集 subset 和最终的结果集 res。
- 回溯（Backtracking）：与 Java 版本一样，这个解决方案使用回溯技术来处理生成子集的过程。

总的来说，要理解这些版本的代码，需要熟悉所用编程语言的基本语法和数据结构，特别是与列表或切片相关的概念。此外，理解递归和回溯的概念对于理解这些解决方案非常重要，因为它们是用于生成子集的关键技术。

79. Word Search

题目

Given a 2D board and a word, find if the word exists in the grid.

The word can be constructed from letters of sequentially adjacent cell, where “adjacent” cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once.

Example:

board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

Given word = "ABCCED", return true.
Given word = "SEE", return true.
Given word = "ABCB", return false.

题目大意

给定一个二维网格和一个单词，找出该单词是否存在于网格中。单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

以下是每个版本的代码的解题思路：

Go 版本解题思路

获取字符矩阵的行数和列数（m 和 n），以及目标单词的长度（l）。
创建一个映射表 bcnts 用于统计字符矩阵中每个字符的出现次数。遍历字符矩阵，将每个字符的出现次数记录在 bcnts 中。
创建一个映射表 wcnts 用于统计目标单词中每个字符的出现次数。遍历目标单词，将每个字符的出现次数记录在 wcnts 中。
检查字符矩阵中的字符是否足够组成目标单词。对于每个字符在 wcnts 中，检查是否存在于 bcnts 中，且其出现次数不小于目标单词中的出现次数。
定义递归函数 f 来搜索目标单词的起始位置。该函数接受当前位置 (x, y)、目标单词的索引 idx 作为参数。
在 f 函数中，首先检查是否已经找到了目标单词，即 idx 是否等于目标单词的长度 l。
然后，检查当前位置 (x, y) 是否越界或已经访问过，以及当前字符是否匹配目标单词的当前字符。
如果当前字符匹配目标单词的字符，将当前字符标记为已访问，然后递归搜索上、下、左、右四个方向。
如果在任何方向上找到了目标单词的路径，返回 true，否则，将当前字符的标记恢复到原始值，返回 false。
在字符矩阵中查找目标单词的起始位置。遍历字符矩阵的每个位置，以该位置为起点调用 f 函数。
如果任何搜索路径找到目标单词，返回 true，否则返回 false，表示未找到目标单词。

Python 版本解题思路

Python 版本的解题思路与 Go 版本基本相同，采用深度优先搜索和递归的方式来查找目标单词。以下是 Python 版本的解题思路：

获取字符矩阵的行数和列数（m 和 n），以及目标单词的长度（l）。
创建一个字典 bcnts 用于统计字符矩阵中每个字符的出现次数。遍历字符矩阵，将每个字符的出现次数记录在 bcnts 中。
创建一个字典 wcnts 用于统计目标单词中每个字符的出现次数。遍历目标单词，将每个字符的出现次数记录在 wcnts 中。
检查字符矩阵中的字符是否足够组成目标单词。对于每个字符在 wcnts 中，检查是否存在于 bcnts 中，且其出现次数不小于目标单词中的出现次数。
定义递归函数 dfs 来搜索目标单词的起始位置。该函数接受当前位置 (x, y)、目标单词的索引 idx 作为参数。
在 dfs 函数中，首先检查是否已经找到了目标单词，即 idx 是否等于目标单词的长度 l。
然后，检查当前位置 (x, y) 是否越界或已经访问过，以及当前字符是否匹配目标单词的当前字符。
如果当前字符匹配目标单词的字符，将当前字符标记为已访问，然后递归搜索上、下、左、右四个方向。
如果在任何方向上找到了目标单词的路径，返回 True，否则，将当前字符的标记恢复到原始值，返回 False。
在字符矩阵中查找目标单词的起始位置。遍历字符矩阵的每个位置，以该位置为起点调用 dfs 函数。
如果任何搜索路径找到目标单词，返回 True，否则返回 False，表示未找到目标单词。

Java 版本解题思路

Java 版本的解题思路与前两个版本相似，同样采用深度优先搜索和递归的方式来查找目标单词。以下是 Java 版本的解题思路：

获取字符矩阵的行数和列数（m 和 n），以及目标单词的长度（l）。
创建一个映射 bcnts 用于统计字符矩阵中每个字符的出现次数。遍历字符矩阵，将每个字符的出现次数记录在 bcnts 中。
创建一个映射 wcnts 用于统计目标单词中每个字符的出现次数。遍历目标单词，将每个字符的出现次数记录在 wcnts 中。
检查字符矩阵中的字符是否足够组成目标单词。对于每个字符在 wcnts 中，检查是否存在于 bcnts 中，且其出现次数不小于目标单词中的出现次数。
创建一个二维布尔数组 visited 用于标记字符矩阵中的字符是否已经被访问过。
定义递归函数 dfs 来搜索目标单词的起始位置。该函数接受当前位置 (x, y)、目标单词的索引 idx 和字符矩阵的可能移动方向 directions 作为参数。
在 dfs 函数中，首先检查是否已经找到了目标单词，即 idx 是否等于目标单词的长度 l。
然后，检查当前位置 (x, y) 是否越界或已经访问过，以及当前字符是否匹配目标单词的当前字符。
如果当前字符匹配目标单词的字符，将当前字符标记为已访问，然后递归搜索可能的移动方向，包括上、下、左、右四个方向。
如果在任何方向上找到了目标单词的路径，返回 true，否则，将当前字符的标记恢复到未访问状态，返回 false。
在字符矩阵中查找目标单词的起始位置。遍历字符矩阵的每个位置，以该位置为起点调用 dfs 函数。
如果任何搜索路径找到目标单词，返回 true，否则返回 false，表示未找到目标单词。

C++ 版本解题思路

C++ 版本的解题思路与前面的版本相似，同样采用深度优先搜索和递归的方式来查找目标单词。以下是 C++ 版本的解题思路：

获取字符矩阵的行数和列数（m 和 n），以及目标单词的长度（l）。
创建一个映射 bcnts 用于统计字符矩阵中每个字符的出现次数。遍历字符矩阵，将每个字符的出现次数记录在 bcnts 中。
创建一个映射 wcnts 用于统计目标单词中每个字符的出现次数。遍历目标单词，将每个字符的出现次数记录在 wcnts 中。
检查字符矩阵中的字符是否足够组成目标单词。对于每个字符在 wcnts 中，检查是否存在于 bcnts 中，且其出现次数不小于目标单词中的出现次数。
创建一个二维布尔数组 visited 用于标记字符矩阵中的字符是否已经被访问过。
定义递归函数 dfs 来搜索目标单词的起始位置。该函数接受当前位置 (x, y)、目标单词的索引 idx 和字符矩阵的可能移动方向 directions 作为参数。
在 dfs 函数中，首先检查是否已经找到了目标单词，即 idx 是否等于目标单词的长度 l。
然后，检查当前位置 (x, y) 是否越界或已经访问过，以及当前字符是否匹配目标单词的当前字符。
如果当前字符匹配目标单词的字符，将当前字符标记为已访问，然后递归搜索可能的移动方向，包括上、下、左、右四个方向。
如果在任何方向上找到了目标单词的路径，返回 true，否则，将当前字符的标记恢复到未访问状态，返回 false。
在字符矩阵中查找目标单词的起始位置。遍历字符矩阵的每个位置，以该位置为起点调用 dfs 函数。
如果任何搜索路径找到目标单词，返回 true，否则返回 false，表示未找到目标单词。

解题思路

在地图上的任意一个起点开始，向 4 个方向分别 DFS 搜索，直到所有的单词字母都找到了就输出 true，否则输出 false。

代码

Go

func exist(board [][]byte, word string) bool {
    // 获取字符矩阵的行数和列数
    m := len(board)
    n := len(board[0])
    // 获取目标单词的长度
    l := len(word)

    // 创建一个映射表，用于统计字符矩阵中每个字符的出现次数
    bcnts := make(map[byte]int)
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            ch := board[i][j]
            _, exists := bcnts[ch]
            if !exists {
                bcnts[ch] = 0
            }
            bcnts[ch] += 1
        }
    }

    // 创建一个映射表，用于统计目标单词中每个字符的出现次数
    wcnts := make(map[byte]int)
    for i := 0; i < l; i++ {
        _, exists := wcnts[word[i]]
        if !exists {
            wcnts[word[i]] = 0
        }
        wcnts[word[i]] += 1
    }

    // 检查字符矩阵中的字符是否足够组成目标单词
    for ch, wcnt := range wcnts {
        bcnt, exists := bcnts[ch]
        if !exists || bcnt < wcnt {
            return false
        }
    }

    // 定义递归函数来搜索目标单词
    var f func(int, int, int) bool
    f = func(x, y int, idx int) bool {
        if idx == l {
            return true  // 已经找到目标单词
        }

        if x < 0 || x >= m || y < 0 || y >= n {
            return false  // 超出字符矩阵边界
        }

        if board[x][y] == '*' {
            return false  // 已经访问过的字符
        }

        if board[x][y] == word[idx] {
            origin := board[x][y]
            board[x][y] = '*'  // 将字符标记为已访问
            if f(x, y-1, idx+1) || f(x, y+1, idx+1) || f(x-1, y, idx+1) || f(x+1, y, idx+1) {
                return true
            }
            board[x][y] = origin  // 恢复字符原始值
        }
        return false
    }

    // 在字符矩阵中查找目标单词的起始位置
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if f(i, j, 0) {
                return true
            }
        }
    }
    return false  // 未找到目标单词
}

Python

class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
        m = len(board)
        n = len(board[0])
        l = len(word)

        bcnts = collections.defaultdict(int)
        for i in range(m):
            for j in range(n):
                ch = board[i][j]
                bcnts[ch] += 1

        wcnts = collections.defaultdict(int)
        for i in range(l):
            wcnts[word[i]] += 1

        for ch, wcnt in wcnts.items():
            if ch not in bcnts or bcnts[ch] < wcnt:
                return False

        def dfs(x, y, idx):
            if idx == l:
                return True

            if x < 0 or x >= m or y < 0 or y >= n:
                return False

            if board[x][y] == '*':
                return False

            if board[x][y] == word[idx]:
                origin = board[x][y]
                board[x][y] = '*'
                if (dfs(x, y - 1, idx + 1) or dfs(x, y + 1, idx + 1) or
                    dfs(x - 1, y, idx + 1) or dfs(x + 1, y, idx + 1)):
                    return True
                board[x][y] = origin

            return False

        for i in range(m):
            for j in range(n):
                if dfs(i, j, 0):
                    return True

        return False

Java

class Solution {
    public boolean exist(char[][] board, String word) {
        int m = board.length;
        int n = board[0].length;
        int l = word.length();

        Map bcnts = new HashMap<>();
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                char ch = board[i][j];
                bcnts.put(ch, bcnts.getOrDefault(ch, 0) + 1);
            }
        }

        Map wcnts = new HashMap<>();
        for (int i = 0; i < l; i++) {
            char ch = word.charAt(i);
            wcnts.put(ch, wcnts.getOrDefault(ch, 0) + 1);
        }

        for (Map.Entry entry : wcnts.entrySet()) {
            char ch = entry.getKey();
            int wcnt = entry.getValue();
            if (!bcnts.containsKey(ch) || bcnts.get(ch) < wcnt) {
                return false;
            }
        }

        boolean[][] visited = new boolean[m][n];

        int[][] directions = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}};

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (dfs(board, word, i, j, 0, visited, directions)) {
                    return true;
                }
            }
        }

        return false;
    }

    private boolean dfs(char[][] board, String word, int x, int y, int idx, boolean[][] visited, int[][] directions) {
        int m = board.length;
        int n = board[0].length;
        int l = word.length();

        if (idx == l) {
            return true;
        }

        if (x < 0 || x >= m || y < 0 || y >= n) {
            return false;
        }

        if (visited[x][y] || board[x][y] != word.charAt(idx)) {
            return false;
        }

        visited[x][y] = true;

        for (int[] direction : directions) {
            int newX = x + direction[0];
            int newY = y + direction[1];
            if (dfs(board, word, newX, newY, idx + 1, visited, directions)) {
                visited[x][y] = false;
                return true;
            }
        }

        visited[x][y] = false;

        return false;
    }
}

Cpp

class Solution {
public:
    bool exist(vector>& board, string word) {
        int m = board.size();
        int n = board[0].size();
        int l = word.length();

        unordered_map bcnts;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                char ch = board[i][j];
                bcnts[ch]++;
            }
        }

        unordered_map wcnts;
        for (int i = 0; i < l; i++) {
            char ch = word[i];
            wcnts[ch]++;
        }

        for (const auto& entry : wcnts) {
            char ch = entry.first;
            int wcnt = entry.second;
            if (bcnts.find(ch) == bcnts.end() || bcnts[ch] < wcnt) {
                return false;
            }
        }

        vector> visited(m, vector(n, false));

        vector> directions = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}};

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (dfs(board, word, i, j, 0, visited, directions)) {
                    return true;
                }
            }
        }

        return false;
    }

private:
    bool dfs(vector>& board, string word, int x, int y, int idx, vector>& visited, vector>& directions) {
        int m = board.size();
        int n = board[0].size();
        int l = word.length();

        if (idx == l) {
            return true;
        }

        if (x < 0 || x >= m || y < 0 || y >= n) {
            return false;
        }

        if (visited[x][y] || board[x][y] != word[idx]) {
            return false;
        }

        visited[x][y] = true;

        for (const vector& direction : directions) {
            int newX = x + direction[0];
            int newY = y + direction[1];
            if (dfs(board, word, newX, newY, idx + 1, visited, directions)) {
                visited[x][y] = false;
                return true;
            }
        }

        visited[x][y] = false;

        return false;
    }
};

当分开介绍每个版本的代码时，我将重点介绍所需的基础知识和概念，以便理解和修改代码。以下是每个版本的详细介绍：

Go 版本

所需基础知识：

基本语法和数据结构：了解 Go 编程语言的基本语法，如变量、循环、条件语句和数据结构（如切片和映射）。
递归和深度优先搜索 (DFS)：了解递归的概念和如何使用递归来实现深度优先搜索（DFS）。
数组切片：了解如何使用数组切片来操作多维数组，以及如何在切片中进行元素的增加和修改。
条件语句：了解条件语句（如 if 语句）的用法，以进行条件检查。

代码解释：

Go 版本的代码使用递归和深度优先搜索来查找目标单词。它使用了两个映射表（bcnts 和 wcnts）来统计字符矩阵和目标单词中每个字符的出现次数。然后，它使用嵌套的递归函数 f 来搜索目标单词的起始位置，并在搜索过程中标记已访问的字符。如果找到目标单词的路径，返回 true，否则返回 false。

Python 版本

所需基础知识：

基本语法和数据结构：了解 Python 编程语言的基本语法，如变量、循环、条件语句和数据结构（如列表和字典）。
递归和深度优先搜索 (DFS)：了解递归的概念和如何使用递归来实现深度优先搜索（DFS）。
列表和字典：了解如何使用列表和字典来存储和操作数据。
类和对象（可选）：理解如何创建和使用类和对象，以便组织代码。

代码解释：

Python 版本的代码与 Go 版本相似，使用递归和深度优先搜索来查找目标单词。它使用字典（collections.defaultdict）来统计字符矩阵和目标单词中每个字符的出现次数。然后，它使用递归函数 dfs 来搜索目标单词的起始位置，标记已访问的字符。如果找到目标单词的路径，返回 true，否则返回 false。

Java 版本

所需基础知识：

基本语法和数据结构：了解 Java 编程语言的基本语法，如变量、循环、条件语句和数据结构（如数组和集合）。
递归和深度优先搜索 (DFS)：了解递归的概念和如何使用递归来实现深度优先搜索（DFS）。
集合框架：了解 Java 的集合框架，如 Map 和 List，以便操作数据集合。
二维数组：了解如何操作二维数组，包括访问元素和遍历。

代码解释：

Java 版本的代码与前两个版本相似，也使用递归和深度优先搜索来查找目标单词。它使用 Map 来统计字符矩阵和目标单词中每个字符的出现次数。然后，它使用递归函数 dfs 来搜索目标单词的起始位置，标记已访问的字符。如果找到目标单词的路径，返回 true，否则返回 false。

C++ 版本

所需基础知识：

基本语法和数据结构：了解 C++ 编程语言的基本语法，如变量、循环、条件语句和数据结构（如向量和映射）。
递归和深度优先搜索 (DFS)：了解递归的概念和如何使用递归来实现深度优先搜索（DFS）。
STL（标准模板库）：了解 C++ 中的标准模板库，包括容器和算法，以便操作数据集合。
多维数组：了解如何操作多维数组，包括访问元素和遍历。

代码解释：

C++ 版本的代码与前面的版本相似，同样使用递归和深度优先搜索来查找目标单词。它使用映射（unordered_map）来统计字符矩阵和目标单词中每个字符的出现次数。然后，它使用递归函数 dfs 来搜索目标单词的起始位置，标记已访问的字符。如果找到目标单词的路径，返回 true，否则返回 false。

需要注意的是，不同版本的代码在语法和数据结构上有一些差异，但它们共同使用深度优先搜索和递归来解决相同的问题。您可以选择其中一个版本，根据您熟悉的编程语言来学习和修改代码。

80. Remove Duplicates from Sorted Array II

题目

Given a sorted array nums, remove the duplicates in-place such that duplicates appeared at most twice and return the new length.

Do not allocate extra space for another array, you must do this by modifying the input array in-place with O(1) extra memory.

Example 1:

Given nums = [1,1,1,2,2,3],

Your function should return length = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.

It doesn't matter what you leave beyond the returned length.

Example 2:

Given nums = [0,0,1,1,1,1,2,3,3],

Your function should return length = 7, with the first seven elements of nums being modified to 0, 0, 1, 1, 2, 3 and 3 respectively.

It doesn't matter what values are set beyond the returned length.

Clarification:

Confused why the returned value is an integer but your answer is an array?

Note that the input array is passed in by reference, which means modification to the input array will be known to the caller as well.

Internally you can think of this:

// nums is passed in by reference. (i.e., without making a copy)
int len = removeElement(nums, val);

// any modification to nums in your function would be known by the caller.
// using the length returned by your function, it prints the first len elements.
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

题目大意

给定一个有序数组 nums，对数组中的元素进行去重，使得原数组中的每个元素最多暴露 2 个。最后返回去重以后数组的长度值。

解题思路

问题提示有序数组，一般最容易想到使用双指针的解法，双指针的关键点：移动两个指针的条件。
在该题中移动的条件：快指针从头遍历数组，慢指针指向修改后的数组的末端，当慢指针指向倒数第二个数与快指针指向的数不相等时，才移动慢指针，同时赋值慢指针。
处理边界条件：当数组小于两个元素时，不做处理。
以下是每个版本的解题思路：

Go 版本解题思路

在Go版本中，我们使用两个指针：slow和fast。slow指针用于跟踪非重复元素的位置，而fast指针用于遍历整个数组。
我们使用for循环和range关键字来遍历数组。在每次迭代中，我们检查两个条件：
- 如果fast小于2（即前两个元素），我们确保这些元素包括在修改后的数组中。
- 如果nums[slow-2]与nums[fast]不相等，我们检查当前元素是否与慢指针指向的位置的前两个元素不同，以确保不超过两个重复元素。
如果上述条件成立，我们将当前元素复制到slow指针的位置，并将slow指针向前移动一个位置。
最后，返回slow指针的值，这个值表示修改后的数组的长度，重复元素已经被移除。

Python 版本解题思路

在Python版本中，我们同样使用两个指针：slow和fast，以及enumerate函数来遍历数组。
我们使用for循环和enumerate函数来遍历数组元素，同时获取元素的索引和值。
在每次迭代中，我们检查两个条件：
- 如果fast小于2（即前两个元素），我们确保这些元素包括在修改后的数组中。
- 如果nums[slow-2]与nums[fast]不相等，我们检查当前元素是否与慢指针指向的位置的前两个元素不同，以确保不超过两个重复元素。
如果上述条件成立，我们将当前元素复制到slow指针的位置，并将slow指针向前移动一个位置。
最后，返回slow指针的值，这个值表示修改后的数组的长度，重复元素已经被移除。

Java 版本解题思路

在Java版本中，我们同样使用两个指针：slow和fast。
使用for循环遍历整个数组。在每次迭代中，检查两个条件：
- 如果fast小于2（即前两个元素），确保这些元素包括在修改后的数组中。
- 如果nums[slow-2]与nums[fast]不相等，检查当前元素是否与慢指针指向的位置的前两个元素不同，以确保不超过两个重复元素。
如果上述条件成立，将当前元素复制到slow指针的位置，并将slow指针向前移动一个位置。
最后，返回slow指针的值，表示修改后的数组的长度，重复元素已被移除。

C++ 版本解题思路

在C++版本中，同样使用两个指针：slow和fast。
使用for循环遍历整个数组。在每次迭代中，检查两个条件：
- 如果fast小于2（即前两个元素），确保这些元素包括在修改后的数组中。
- 如果nums[slow-2]与nums[fast]不相等，检查当前元素是否与慢指针指向的位置的前两个元素不同，以确保不超过两个重复元素。
如果上述条件成立，将当前元素复制到slow指针的位置，并将slow指针向前移动一个位置。
最后，返回slow指针的值，表示修改后的数组的长度，重复元素已被移除。

这些解题思路都基于双指针的概念，遍历有序数组并进行去重操作，确保重复元素最多出现两次。在满足条件的情况下，通过适当地移动指针和复制元素，最终返回修改后的数组的长度。

代码

Go

func removeDuplicates(nums []int) int {
    slow := 0  // 定义慢指针，用于跟踪非重复元素的位置
    for fast, v := range nums {  // 使用快指针遍历整个数组
        if fast < 2 || nums[slow-2] != v {  // 如果快指针小于2（前两个元素），或者慢指针指向的元素与当前元素不相同
            nums[slow] = v  // 将当前元素复制到慢指针位置
            slow++  // 移动慢指针，指向下一个位置
        }
    }
    return slow  // 返回去重后数组的长度
}

Python

from typing import List

class Solution:
    def removeDuplicates(self, nums: List[int]) -> int:
        slow = 0  # 定义慢指针，用于跟踪非重复元素的位置
        for fast, v in enumerate(nums):  # 使用快指针遍历整个数组
            if fast < 2 or nums[slow - 2] != v:  # 如果快指针小于2（前两个元素），或者慢指针指向的元素与当前元素不相同
                nums[slow] = v  # 将当前元素复制到慢指针位置
                slow += 1  # 移动慢指针，指向下一个位置
        return slow  # 返回去重后数组的长度

Java

class Solution {
    public int removeDuplicates(int[] nums) {
        int slow = 0; // 定义慢指针，用于跟踪非重复元素的位置
        for (int fast = 0; fast < nums.length; fast++) { // 使用快指针遍历整个数组
            if (fast < 2 || nums[slow - 2] != nums[fast]) { // 如果快指针小于2（前两个元素），或者慢指针指向的元素与当前元素不相同
                nums[slow] = nums[fast]; // 将当前元素复制到慢指针位置
                slow++; // 移动慢指针，指向下一个位置
            }
        }
        return slow; // 返回去重后数组的长度
    }
}

Cpp

class Solution {
public:
    int removeDuplicates(vector& nums) {
        int slow = 0; // 定义慢指针，用于跟踪非重复元素的位置
        for (int fast = 0; fast < nums.size(); fast++) { // 使用快指针遍历整个数组
            if (fast < 2 || nums[slow - 2] != nums[fast]) { // 如果快指针小于2（前两个元素），或者慢指针指向的元素与当前元素不相同
                nums[slow] = nums[fast]; // 将当前元素复制到慢指针位置
                slow++; // 移动慢指针，指向下一个位置
            }
        }
        return slow; // 返回去重后数组的长度
    }
};

理解和实现这个题目的解法需要掌握以下基础知识：

Go 版本

切片（Slices）： 了解如何使用切片来操作数组，包括创建、切片、遍历切片等。在Go中，切片是动态数组，经常用于解决数组长度不确定的情况。
for-range 循环： 了解如何使用 for 循环和 range 关键字来遍历数组的元素。

Python 版本

列表（Lists）： 了解如何使用列表来操作数组，包括创建、切片、遍历列表等。在Python中，列表是一种灵活的数据结构，用于存储序列数据。
enumerate 函数： 了解如何使用 enumerate 函数来同时获取元素的索引和值，这对于在循环中处理数组元素非常有用。
类和方法： 了解如何定义类和方法，尤其是在实现类似面向对象的解决方案时。

Java 版本

数组： 了解如何声明和初始化数组，以及如何使用数组的索引来访问元素。
for 循环： 了解如何使用 for 循环来遍历数组，以及如何在循环中处理数组元素。

C++ 版本

数组： 了解如何声明和初始化数组，以及如何使用数组的索引来访问元素。
for 循环： 了解如何使用 for 循环来遍历数组，以及如何在循环中处理数组元素。
类和方法： 了解如何定义类和方法，尤其是在实现类似面向对象的解决方案时。

这些基础知识是理解和实现题目解法的关键，无论选择哪种编程语言版本，都需要熟练掌握这些概念。另外，对于特定语言的版本，还需要了解相关语言的语法和特性，如切片、列表、类和方法等。

81. Search in Rotated Sorted Array II

题目

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e., [0,0,1,2,2,5,6] might become [2,5,6,0,0,1,2]).

You are given a target value to search. If found in the array return true, otherwise return false.

Example 1:

Input: nums = [2,5,6,0,0,1,2], target = 0
Output: true

Example 2:

Input: nums = [2,5,6,0,0,1,2], target = 3
Output: false

Follow up:

This is a follow up problem to Search in Rotated Sorted Array, where nums may contain duplicates.
Would this affect the run-time complexity? How and why?

题目大意

假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如，数组 [0,0,1,2,2,5,6] 可能变为 [2,5,6,0,0,1,2] )。

编写一个函数来判断给定的目标值是否存在于数组中。若存在返回 true，否则返回 false。

进阶:

这是搜索旋转排序数组的延伸题目，本题中的 nums 可能包含重复元素。
这会影响到程序的时间复杂度吗？会有怎样的影响，为什么？

解题思路

给出一个数组，数组中本来是从小到大排列的，并且数组中有重复数字。但是现在把后面随机一段有序的放到数组前面，这样形成了前后两端有序的子序列。在这样的一个数组里面查找一个数，设计一个 O(log n) 的算法。如果找到就输出 true，如果没有找到，就输出 false 。
这一题是第 33 题的加强版，实现代码完全一样，只不过输出变了。这一题输出 true 和 false 了。具体思路见第 33 题。

以下是每个版本的解题思路：

Go 版本：

初始化指针： 首先，初始化两个指针 low 和 high，分别指向数组的第一个元素和最后一个元素。
进入循环： 使用循环，直到 low 大于 high 为止。
计算中间索引： 计算中间索引 mid，通过 (low + (high - low) >> 1) 来避免整数溢出。
检查中间元素： 检查中间元素是否等于目标元素，如果是，返回 true，因为找到了目标。
处理两部分情况： 如果中间元素不等于目标，需要根据数组的性质将搜索范围缩小到左半部分或右半部分。

a. 如果 nums[mid] > nums[low]，说明左半部分是有序的。在这种情况下，检查目标是否在 low 和 mid 之间，如果是，将 high 更新为 mid - 1，否则将 low 更新为 mid + 1。

b. 如果 nums[mid] < nums[high]，说明右半部分是有序的。在这种情况下，检查目标是否在 mid 和 high 之间，如果是，将 low 更新为 mid + 1，否则将 high 更新为 mid - 1。

c. 处理重复的情况：如果 nums[low] 等于 nums[mid]，将 low 指针向右移动一位；如果 nums[high] 等于 nums[mid]，将 high 指针向左移动一位。
返回结果： 如果循循环结束后仍未找到目标元素，返回 false，因为目标不在数组中。

Python 版本：

初始化指针和处理边界情况： 首先，初始化指针 start 和 end 分别指向数组的第一个元素和最后一个元素。还需要处理特殊情况，例如数组为空或只包含一个元素。
进入循环： 使用循环，直到 start 大于 end 为止。
计算中间索引： 计算中间索引 half，通过 (start + end) // 2 来找到中间元素的索引。
检查中间元素： 检查中间元素是否等于目标元素，如果是，返回 True，因为找到了目标。
处理两部分情况： 如果中间元素不等于目标，需要根据数组的性质将搜索范围缩小到左半部分或右半部分。

a. 如果 nums[start] 等于 nums[half] 且 nums[half] 等于 nums[end]，这表示存在重复元素。在这种情况下，将 start 向右移动一位，将 end 向左移动一位。

b. 如果 nums[start] 小于等于 nums[half]，说明左半部分是有序的。检查目标是否在这个有序部分内。如果是，将 end 更新为 half - 1，否则将 start 更新为 half + 1。

c. 如果 nums[half] 小于 nums[end]，说明右半部分是有序的。检查目标是否在这个有序部分内。如果是，将 start 更新为 half + 1，否则将 end 更新为 half - 1。
返回结果： 如果循环结束后仍未找到目标元素，返回 False，因为目标不在数组中。

Java 版本：

初始化指针和处理边界情况： 首先，初始化指针 low 和 high 分别指向数组的第一个元素和最后一个元素。还需要处理特殊情况，例如数组为空或只包含一个元素。
进入循环： 使用循环，直到 low 大于 high 为止。
计算中间索引： 计算中间索引 mid，通过 (low + (high - low) / 2) 来找到中间元素的索引。
检查中间元素： 检查中间元素是否等于目标元素，如果是，返回 true，因为找到了目标。
处理两部分情况： 如果中间元素不等于目标，需要根据数组的性质将搜索范围缩小到左半部分或右半部分。

a. 如果 nums[mid] > nums[low]，说明左半部分是有序的。在这种情况下，检查目标是否在 low 和 mid 之间，如果是，将 high 更新为 mid - 1，否则将 low 更新为 mid + 1。

b. 如果 nums[mid] < nums[high]，说明右半部分是有序的。在这种情况下，检查目标是否在 mid 和 high 之间，如果是，将 low 更新为 mid + 1，否则将 high 更新为 mid - 1。

c. 处理重复的情况：如果 nums[low] 等于 nums[mid]，将 low 指针向右移动一位；如果 nums[high] 等于 nums[mid]，将 high 指针向左移动一位。
返回结果： 如果循环结束后仍未找到目标元素，返回 false，因为目标不在数组中。

C++ 版本：

初始化指针和处理边界情况： 首先，初始化指针 low 和 high 分别指向数组的第一个元素和最后一个元素。还需要处理特殊情况，例如数组为空或只包含一个元素。
进入循环： 使用循环，直到 low 大于 high 为止。
计算中间索引： 计算中间索引 mid，通过 (low + (high - low) / 2) 来找到中间元素的索引。
检查中间元素： 检查中间元素是否等于目标元素，如果是，返回 true，因为找到了目标。
处理两部分情况： 如果中间元素不等于目标，需要根据数组的性质将搜索范围缩小到左半部分或右半部分。

a. 如果 nums[mid] > nums[low]，说明左半部分是有序的。在这种情况下，检查目标是否在 low 和 mid 之间，如果是，将 high 更新为 mid - 1，否则将 low 更新为 mid + 1。

b. 如果 nums[mid] < nums[high]，说明右半部分是有序的。在这种情况下，检查目标是否在 mid 和 high 之间，如果是，将 low 更新为 mid + 1，否则将 high 更新为 mid - 1。

c. 处理重复的情况：如果 nums[low] 等于 nums[mid]，将 low 指针向右移动一位；如果 nums[high] 等于 nums[mid]，将 high 指针向左移动一位。
返回结果： 如果循环结束后仍未找到目标元素，返回 false，因为目标不在数组中。

总的来说，这些解题思路都涉及初始化指针，使用二分查找的思想，适应不同编程语言的语法和数据结构，以解决旋转有序数组中的目标查找问题。处理重复元素和边界情况是解题的关键点，同时需要理解二分查找算法的核心思想。

代码

Go

func search(nums []int, target int) bool {
	if len(nums) == 0 {
		return false
	}
	// 初始化两个指针，low指向数组的第一个元素，high指向数组的最后一个元素
	low, high := 0, len(nums)-1
	// 进入循环，直到low大于high时结束
	for low <= high {
		// 计算中间索引
		mid := low + (high-low)>>1
		// 如果中间元素等于目标元素，则返回true
		if nums[mid] == target {
			return true
		} else if nums[mid] > nums[low] { // 在数值大的一部分区间里
			// 如果目标元素在low和mid之间，缩小搜索范围为low到mid-1
			if nums[low] <= target && target < nums[mid] {
				high = mid - 1
			} else {
				// 否则，缩小搜索范围为mid+1到high
				low = mid + 1
			}
		} else if nums[mid] < nums[high] { // 在数值小的一部分区间里
			// 如果目标元素在mid和high之间，缩小搜索范围为mid+1到high
			if nums[mid] < target && target <= nums[high] {
				low = mid + 1
			} else {
				// 否则，缩小搜索范围为low到mid-1
				high = mid - 1
			}
		} else {
			// 处理重复的情况
			// 如果nums[low]等于nums[mid]，将low指针向右移动一位
			if nums[low] == nums[mid] {
				low++
			}
			// 如果nums[high]等于nums[mid]，将high指针向左移动一位
			if nums[high] == nums[mid] {
				high--
			}
		}
	}
	// 如果循环结束仍未找到目标元素，返回false
	return false
}

Python

class Solution:
    def search(self, nums: List[int], target: int) -> bool:
        start = 0
        end = len(nums) - 1

        if len(nums) == 0:
            return False

        if len(nums) == 1:
            return nums[0] == target

        while(start <= end):
            half = (start + end) // 2
            if nums[half] == target:
                return True

            if nums[start] == nums[half] and nums[half] == nums[end]:
                # 处理重复元素的情况
                start += 1
                end -= 1
            elif nums[start] <= nums[half]:
                if nums[start] <= target and nums[half] > target:
                    # 目标值在有序部分
                    end = half - 1
                else:
                    # 目标值在旋转部分
                    start = half + 1
            else:
                if nums[half] < target and nums[end] >= target:
                    # 目标值在有序部分
                    start = half + 1
                else:
                    # 目标值在旋转部分
                    end = half - 1

        return False

Java

class Solution {
    public boolean search(int[] nums, int target) {
        if (nums.length == 0) {
            return false;
        }
        int low = 0, high = nums.length - 1;
        while (low <= high) {
            int mid = low + (high - low) / 2;
            if (nums[mid] == target) {
                return true;
            } else if (nums[mid] > nums[low]) {
                if (nums[low] <= target && target < nums[mid]) {
                    high = mid - 1;
                } else {
                    low = mid + 1;
                }
            } else if (nums[mid] < nums[high]) {
                if (nums[mid] < target && target <= nums[high]) {
                    low = mid + 1;
                } else {
                    high = mid - 1;
                }
            } else {
                if (nums[low] == nums[mid]) {
                    low++;
                }
                if (nums[high] == nums[mid]) {
                    high--;
                }
            }
        }
        return false;
    }
}

Cpp

class Solution {
public:
    bool search(vector& nums, int target) {
        if (nums.empty()) {
            return false;
        }
        int low = 0, high = nums.size() - 1;
        while (low <= high) {
            int mid = low + (high - low) / 2;
            if (nums[mid] == target) {
                return true;
            } else if (nums[mid] > nums[low]) {
                if (nums[low] <= target && target < nums[mid]) {
                    high = mid - 1;
                } else {
                    low = mid + 1;
                }
            } else if (nums[mid] < nums[high]) {
                if (nums[mid] < target && target <= nums[high]) {
                    low = mid + 1;
                } else {
                    high = mid - 1;
                }
            } else {
                if (nums[low] == nums[mid]) {
                    low++;
                }
                if (nums[high] == nums[mid]) {
                    high--;
                }
            }
        }
        return false;
    }
};

当使用不同的编程语言来解决算法问题时，需要了解各个语言的基本语法和数据结构。以下是每个版本的需要掌握的基础知识：

Go 版本：

数组和切片： 在 Go 中，数组是固定长度的数据结构，切片则是动态长度的。你需要理解如何声明、初始化和操作数组和切片，因为算法问题通常需要对数据结构进行操作。
循环和条件语句： 了解 Go 中的 for 循环和 if 条件语句的用法，因为它们在算法实现中经常用到。
函数： 熟悉如何定义和调用函数。算法通常被封装为函数，因此需要了解如何传递参数和返回值。
二分查找： 了解二分查找算法的工作原理，因为这是该问题的关键部分。

Python 版本：

列表： Python 中的列表是动态数组，因此需要知道如何声明、初始化和操作列表。
循环和条件语句： 了解 Python 中的 for 循环和 if 条件语句的使用方法，因为它们在算法实现中经常用到。
类和对象： Python 是一门面向对象的编程语言，了解如何定义类和对象是很有用的，尤其是对于面向对象的编程问题。
二分查找： 理解二分查找算法的工作原理，因为这是解决问题的核心算法。

Java 版本：

数组和列表： Java 中有数组和 ArrayList 这两种数据结构，需要了解如何声明、初始化和操作它们。
循环和条件语句： 了解 Java 中的 for 循环和 if 条件语句的用法，因为它们在算法实现中经常用到。
类和对象： Java 是一门面向对象的编程语言，需要了解如何定义类和对象，尤其是对于面向对象的编程问题。
二分查找： 了解二分查找算法的工作原理，因为这是解决问题的核心算法。

C++ 版本：

数组和向量： C++ 中有数组和 vector 这两种数据结构，需要了解如何声明、初始化和操作它们。
循环和条件语句： 了解 C++ 中的 for 循环和 if 条件语句的用法，因为它们在算法实现中经常用到。
类和对象： C++ 是一门支持面向对象编程的语言，需要了解如何定义类和对象，尤其是对于面向对象的编程问题。
二分查找： 了解二分查找算法的工作原理，因为这是解决问题的核心算法。

总的来说，了解基本的编程概念，掌握循环、条件语句和数据结构的使用，以及理解特定算法的工作原理对解决算法问题非常重要。无论使用哪种编程语言，这些基本知识都是通用的。

82. Remove Duplicates from Sorted List II

题目

Given a sorted linked list, delete all nodes that have duplicate numbers, leaving only distinct numbers from the original list.

Example 1:

Input: 1->2->3->3->4->4->5
Output: 1->2->5

Example 2:

Input: 1->1->1->2->3
Output: 2->3

题目大意

删除链表中重复的结点，只要是有重复过的结点，全部删除。

解题思路

以下是每个版本的解题思路的详细介绍：

Go版本解题思路：

创建一个新的头节点 newHead，并将其指向原始链表的头节点 head。这样可以简化处理边界情况。
使用指针 cur 指向当前处理的节点，指针 last 指向当前节点的前一个节点，以及指针 front 用于遍历链表。
遍历链表，直到 front 到达链表末尾。
在遍历过程中，检查当前节点的值是否与前一个节点的值相同，以确定是否有重复节点。
如果当前节点的值与前一个节点的值相同，继续遍历到下一个节点，跳过重复节点。
如果当前节点的值与前一个节点的值不同，根据情况更新指针和连接。如果当前节点与前一个节点之间存在重复节点，将 last 指向当前不重复的节点，并更新 cur 指向当前节点。如果没有重复节点，正常移动三个指针。
处理链表末尾可能存在的重复节点，确保正确的连接关系。
最后，返回处理后的链表，即 newHead.Next。

Python版本解题思路：

创建一个虚拟节点 dummy，将其 next 指向原始链表的头节点 head。
遍历链表，同时维护指针 cur 指向当前处理的节点。
在循环中，检查当前节点和下一个节点是否有相同的值。
如果有相同的值，继续向下移动，直到找到不同的值。
如果值不同，更新指针 cur 到下一个节点，继续遍历。
最后，返回虚拟节点 dummy 的下一个节点，这是去除重复元素后的链表。

Java版本解题思路：

创建一个新的头节点 newHead，并将其指向原始链表的头节点 head。这样可以简化处理边界情况。
使用指针 cur 指向当前处理的节点，指针 last 指向当前节点的前一个节点，以及指针 front 用于遍历链表。
遍历链表，直到 front 到达链表末尾。
在遍历过程中，检查当前节点的值是否与前一个节点的值相同，以确定是否有重复节点。
如果当前节点的值与前一个节点的值相同，继续遍历到下一个节点，跳过重复节点。
如果当前节点的值与前一个节点的值不同，根据情况更新指针和连接。如果当前节点与前一个节点之间存在重复节点，将 last.next 指向当前不重复的节点，并更新 cur 指向当前节点。如果没有重复节点，正常移动三个指针。
处理链表末尾可能存在的重复节点，确保正确的连接关系。
最后，返回处理后的链表，即 newHead.next。

C++版本解题思路：

创建一个新的头节点 newHead，并将其指向原始链表的头节点 head。这样可以简化处理边界情况。
使用指针 cur 指向当前处理的节点，指针 last 指向当前节点的前一个节点，以及指针 front 用于遍历链表。
遍历链表，直到 front 到达链表末尾。
在遍历过程中，检查当前节点的值是否与前一个节点的值相同，以确定是否有重复节点。
如果当前节点的值与前一个节点的值相同，继续遍历到下一个节点，跳过重复节点。
如果当前节点的值与前一个节点的值不同，根据情况更新指针和连接。如果当前节点与前一个节点之间存在重复节点，将 last->next 指向当前不重复的节点，并更新 cur 指向当前节点。如果没有重复节点，正常移动三个指针。
处理链表末尾可能存在的重复节点，确保正确的连接关系。
最后，返回处理后的链表，即 newHead->next。

每个版本的解题思路都涉及创建新头节点、维护多个指针来处理重复节点，以及正确连接不重复节点的关键逻辑。此外，还需要理解链表的基本概念和相应编程语言的语法特性。

代码

Go

func deleteDuplicates1(head *ListNode) *ListNode {
	if head == nil {
		return nil
	}
	if head.Next == nil {
		return head
	}
	newHead := &ListNode{Next: head, Val: -999999} // 创建一个新的头节点，值设置为一个不可能出现在链表中的值，以简化边界情况处理
	cur := newHead // cur 指向当前处理的节点
	last := newHead // last 指向当前节点的前一个节点
	front := head // front 用于遍历链表

for front.Next != nil { // 遍历链表直到 front 到达链表末尾
		if front.Val == cur.Val { // 如果当前节点的值与前一个节点的值相同，表示有重复节点
			front = front.Next // 移动到下一个节点
			continue
		} else { // 如果当前节点的值与前一个节点的值不同
			if cur.Next != front { // 如果当前节点与前一个节点之间有重复节点
				last.Next = front // 跳过重复节点，将上一个节点指向当前不重复的节点
				if front.Next != nil && front.Next.Val != front.Val {
					last = front // 更新 last 指针，因为当前节点可能是下一个不同值节点的前一个节点
				}
				cur = front // 更新 cur 指针到当前不重复的节点
				front = front.Next // 移动到下一个节点
			} else { // 常规情况，没有重复节点
				last = cur // 更新 last 指针
				cur = cur.Next // 更新 cur 指针到下一个节点
				front = front.Next // 移动到下一个节点
			}
		}
	}
	if front.Val == cur.Val { // 处理链表末尾可能存在的重复节点
		last.Next = nil // 移除重复节点
	} else {
		if cur.Next != front { // 处理链表末尾的不同值节点
			last.Next = front // 将 last 指向末尾不同值节点
		}
	}
	return newHead.Next // 返回处理后的链表
}

Python

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next

class Solution:
    def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:
        # 创建一个虚拟节点 dummy，其 next 指向原始链表的头节点 head
        dummy = cur = ListNode(next = head)

        # 遍历链表
        while cur.next and cur.next.next:
            val = cur.next.val

            # 如果当前节点的值与下一个节点的值相同
            if cur.next.val == cur.next.next.val:
                # 移动 cur.next 直到找到不同的值
                while cur.next and cur.next.val == val:
                    cur.next = cur.next.next
            else:
                # 如果当前节点的值与下一个节点的值不同，继续遍历链表
                cur = cur.next

        # 返回虚拟节点的下一个节点，即去除重复元素后的链表
        return dummy.next

Java

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        if (head == null) {
            return null;
        }
        if (head.next == null) {
            return head;
        }
        ListNode newHead = new ListNode(-999999);
        newHead.next = head;
        ListNode cur = newHead;
        ListNode last = newHead;
        ListNode front = head;
        while (front.next != null) {
            if (front.val == cur.val) {
                front = front.next;
                continue;
            } else {
                if (cur.next != front) {
                    last.next = front;
                    if (front.next != null && front.next.val != front.val) {
                        last = front;
                    }
                    cur = front;
                    front = front.next;
                } else {
                    last = cur;
                    cur = cur.next;
                    front = front.next;
                }
            }
        }
        if (front.val == cur.val) {
            last.next = null;
        } else {
            if (cur.next != front) {
                last.next = front;
            }
        }
        return newHead.next;
    }
}

Cpp

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode* next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode* next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        if (!head) {
            return nullptr;
        }
        if (!head->next) {
            return head;
        }
        ListNode* newHead = new ListNode(-999999);
        newHead->next = head;
        ListNode* cur = newHead;
        ListNode* last = newHead;
        ListNode* front = head;
        while (front->next) {
            if (front->val == cur->val) {
                front = front->next;
                continue;
            } else {
                if (cur->next != front) {
                    last->next = front;
                    if (front->next && front->next->val != front->val) {
                        last = front;
                    }
                    cur = front;
                    front = front->next;
                } else {
                    last = cur;
                    cur = cur->next;
                    front = front->next;
                }
            }
        }
        if (front->val == cur->val) {
            last->next = nullptr;
        } else {
            if (cur->next != front) {
                last->next = front;
            }
        }
        return newHead->next;
    }
};

理解每个版本的代码所需的基础知识可以有所不同，以下是每个版本的详细介绍：

Go版本：

基本Go语法：了解Go的基本语法，如变量声明、条件语句、循环、函数定义、指针、结构体等。
链表：理解链表的概念，包括单链表和节点的结构。了解如何创建、访问和遍历链表。
指针：了解Go中的指针操作，包括如何创建指针、访问结构体字段等。
循环：理解for循环以及如何在循环中遍历链表。

Python版本：

Python基础语法：了解Python的基本语法，包括变量、条件语句、循环、类和对象、列表等。
链表：理解链表的概念，包括单链表和节点的结构。了解如何创建、访问和遍历链表。
类和对象：了解Python中如何创建类和对象，以及如何定义类的方法。
循环：理解while循环和for循环，以及如何在循环中遍历链表。

Java版本：

Java基础语法：了解Java的基本语法，包括类、方法、变量、条件语句、循环、对象等。
链表：理解链表的概念，包括单链表和节点的结构。了解如何创建、访问和遍历链表。
类和对象：了解如何创建类和对象，以及如何定义类的构造函数和方法。
链表操作：理解Java中如何操作链表，包括创建新节点、更改节点的指针等。

C++版本：

C++基础语法：了解C++的基本语法，包括类、方法、变量、条件语句、循环、指针等。
链表：理解链表的概念，包括单链表和节点的结构。了解如何创建、访问和遍历链表。
类和对象：了解C++中如何创建类和对象，以及如何定义类的构造函数和方法。
指针：了解C++中的指针操作，包括如何创建指针、访问结构体字段等。
动态内存分配：了解如何使用new和delete来进行动态内存分配和释放，以确保内存管理。

每个版本的代码都涉及链表数据结构的操作，以及相应编程语言的语法和特性。因此，理解链表的基本概念以及编程语言的基础知识对于理解和实现这些版本的代码都是必要的。

83. Remove Duplicates from Sorted List

题目

Given a sorted linked list, delete all duplicates such that each element appear only once.

Example 1:

Input: 1->1->2
Output: 1->2

Example 2:

Input: 1->1->2->3->3
Output: 1->2->3

题目大意

删除链表中重复的结点，以保障每个结点只出现一次。

解题思路

当然可以，接下来我将为您分别介绍每个版本的解题思路。

解题思路:
1. 首先检查链表是否为空或只有一个节点，如果是，则直接返回原链表，因为没有重复值需要删除。
2. 递归地对当前节点的下一个节点调用deleteDuplicates函数，这样可以确保从当前节点开始的所有后续节点都不包含重复值。
3. 在递归返回后，比较当前节点与其下一个节点的值。如果它们的值相同，则将当前节点的next指针设置为下一个节点的next指针，从而跳过下一个节点。
4. 返回处理后的链表头节点。

Python

解题思路:
1. 首先检查链表是否为空，如果是，则直接返回。
2. 用entry变量引用当前节点的下一个节点。
3. 如果entry不为None，那么比较当前节点和entry的值。
4. 如果它们的值相同，则将当前节点的next指向entry的next，从而跳过entry节点。
5. 递归地对当前节点调用deleteDuplicates函数，这样可以确保从当前节点开始的所有节点都不包含重复值。
6. 如果当前节点和entry的值不同，则递归地对entry调用deleteDuplicates函数。

Java

解题思路:
1. 首先检查链表是否为空或只有一个节点，如果是，则直接返回原链表。
2. 递归地对当前节点的下一个节点调用deleteDuplicates函数。
3. 在递归返回后，比较当前节点与其下一个节点的值。如果它们的值相同，则将当前节点的next指针设置为下一个节点的next指针。
4. 返回处理后的链表头节点。

解题思路:
1. 首先检查链表是否为空或只有一个节点，如果是，则直接返回原链表。
2. 递归地对当前节点的下一个节点调用deleteDuplicates函数。
3. 在递归返回后，比较当前节点与其下一个节点的值。如果它们的值相同，则将当前节点的next指针设置为下一个节点的next指针。
4. 返回处理后的链表头节点。

对于这四种语言版本，解题思路基本是相同的，主要的区别在于语言语法和具体实现细节。

代码

Go

/**
 * 链表节点的定义
 * type ListNode struct {
 *     Val int           // 节点的值
 *     Next *ListNode    // 指向下一个节点的指针
 * }
 */
func deleteDuplicates(head *ListNode) *ListNode {
    // 如果链表为空或者只有一个节点，直接返回原链表
    if head == nil || head.Next == nil {
        return head
    }
    
    // 递归调用，删除链表中从第二个节点开始的重复元素
    head.Next = deleteDuplicates(head.Next)
    
    // 如果当前节点的值与下一个节点的值相同，删除当前节点
    if head.Val == head.Next.Val {
        head = head.Next
    }
    
    return head
}

Python

class Solution:
    def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:
        # 如果链表为空，直接返回
        if not head:
            return head

        # entry是当前节点的下一个节点
        entry = head.next

        # 如果有下一个节点
        if entry:
            # 如果当前节点的值与下一个节点的值相同
            if head.val == entry.val:
                # 跳过下一个节点，将当前节点的next指向下一个节点的下一个节点
                head.next = entry.next
                # 递归调用，继续处理当前节点，因为它可能还有重复元素
                self.deleteDuplicates(head)
            else:
                # 如果当前节点的值与下一个节点的值不同，递归调用处理下一个节点
                self.deleteDuplicates(entry)
        
        # 返回处理后的链表头节点
        return head

Java

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        // 如果链表为空或者只有一个节点，直接返回原链表
        if (head == null || head.next == null) {
            return head;
        }
        
        // 递归调用，删除链表中从第二个节点开始的重复元素
        head.next = deleteDuplicates(head.next);
        
        // 如果当前节点的值与下一个节点的值相同，删除当前节点
        if (head.val == head.next.val) {
            head = head.next;
        }
        
        return head;
    }
}

Cpp

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        // 如果链表为空或者只有一个节点，直接返回原链表
        if (head == nullptr || head->next == nullptr) {
            return head;
        }
        
        // 递归调用，删除链表中从第二个节点开始的重复元素
        head->next = deleteDuplicates(head->next);
        
        // 如果当前节点的值与下一个节点的值相同，删除当前节点
        if (head->val == head->next->val) {
            head = head->next;
        }
        
        return head;
    }
};

好的，接下来我会分别为Go、Python、Java和Cpp版本的代码解释所需掌握的基础知识。

1. Go

基础知识:
- Go语言的基本语法，包括数据类型、变量、条件语句和循环。
- Go语言中的指针概念。在这个题目中，链表节点是通过指针进行连接的。
- Go语言的结构体。ListNode是一个结构体，用于表示链表节点。
- Go语言的递归函数。deleteDuplicates函数是递归的。

2. Python

基础知识:
- Python的基本语法，包括数据类型、变量、条件语句和循环。
- Python中的类和对象。在这个题目中，ListNode是一个类，用于表示链表节点。
- Python中的self关键字。它用于引用对象的当前实例。
- Python的递归函数。deleteDuplicates方法是递归的。

3. Java

基础知识:
- Java的基本语法，包括数据类型、变量、条件语句和循环。
- Java中的类和对象。ListNode和Solution都是类。
- Java中的访问修饰符，如public。
- Java中的构造方法。ListNode类中有多个构造方法。
- Java的递归函数。deleteDuplicates方法是递归的。

4. Cpp

基础知识:
- C++的基本语法，包括数据类型、变量、条件语句和循环。
- C++中的指针和引用。在这个题目中，链表节点是通过指针进行连接的。
- C++中的类和对象。ListNode和Solution都是类。
- C++中的构造函数和析构函数。ListNode类中有多个构造函数。
- C++的递归函数。deleteDuplicates方法是递归的。

对于每种语言，如果想深入理解和掌握这个题目和代码，你还需要对数据结构中的链表有所了解，包括链表的基本操作（如插入、删除节点）和常见的链表问题。

84. Largest Rectangle in Histogram

题目

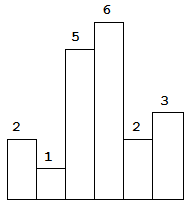
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

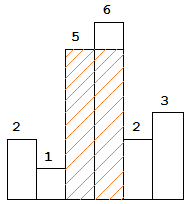
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

The largest rectangle is shown in the shaded area, which has area = 10 unit.

Example:

Input: [2,1,5,6,2,3]
Output: 10

题目大意

给出每个直方图的高度，要求在这些直方图之中找到面积最大的矩形，输出矩形的面积。

解题思路

用单调栈依次保存直方图的高度下标，一旦出现高度比栈顶元素小的情况就取出栈顶元素，单独计算一下这个栈顶元素的矩形的高度。然后停在这里(外层循环中的 i–，再 ++，就相当于停在这里了)，继续取出当前最大栈顶的前一个元素，即连续弹出 2 个最大的，以稍小的一个作为矩形的边，宽就是 2 计算面积…………如果停在这里的下标代表的高度一直比栈里面的元素小，就一直弹出，取出最后一个比当前下标大的高度作为矩形的边。宽就是最后一个比当前下标大的高度和当前下标 i 的差值。计算出面积以后不断的更新 maxArea 即可。

代码

Go

func largestRectangleArea(heights []int) int {
	maxArea := 0  // 初始化最大矩形面积为0
	n := len(heights) + 2  // 计算直方图的长度，并在两端各添加一个哨兵节点
	// 添加一个函数getHeight，用于获取某个位置的高度，如果是哨兵节点则返回0
	getHeight := func(i int) int {
		if i == 0 || n-1 == i {
			return 0
		}
		return heights[i-1]
	}
	st := make([]int, 0, n/2)  // 创建一个用于保存直方图高度索引的栈
	for i := 0; i < n; i++ {
		for len(st) > 0 && getHeight(st[len(st)-1]) > getHeight(i) {
			// 如果栈不为空且栈顶高度大于当前高度，则出栈
			idx := st[len(st)-1]  // 获取栈顶索引
			st = st[:len(st)-1]  // 出栈
			maxArea = max(maxArea, getHeight(idx)*(i-st[len(st)-1]-1))  // 计算矩形面积并更新最大面积
		}
		// 将当前索引入栈
		st = append(st, i)
	}
	return maxArea  // 返回最大矩形面积
}

func max(a int, b int) int {
	if a > b {
		return a
	}
	return b
}

Python

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        max_h=max(heights)
        min_h=min(heights)
        if max_h==min_h:
            return max_h*len(heights)
        stack = [-1]
        heights.append(0)
        mxarea = 0
        for i, v in enumerate(heights):
            while heights[stack[-1]] > v:
                mid = stack.pop()
                area = heights[mid] * (i - 1 - stack[-1])
                if area > mxarea: mxarea = area
            stack.append(i)
        return mxarea

Java

class Solution {
    public int largestRectangleArea(int[] heights) {
        //也很经典
        int n = heights.length;
        int[] stack = new int[n + 1];
        int top = 0;
        int res = 0;
        for (int i = 0; i < n; i++) {
            while (top > 0 && heights[i] <= heights[stack[top]]) {
                int temp = stack[top--];
                res = Math.max(res, (i - (top == 0 ? -1 : stack[top]) - 1)  * heights[temp]);
            }
            stack[++top] = i;
        }
        while (top > 0) {
            int temp = stack[top--];
            res = Math.max(res, (n - (top == 0 ? -1 : stack[top]) - 1) * heights[temp]);
        }
        return res;
    }
}

Cpp

#define let     const auto
int pos[100005];

class Solution {
public:
    int largestRectangleArea(vector& heights) {
        heights.push_back(0);
        const int n = heights.size();
        int sp = -1;
        int ans = 0;
        for(int i = 0; i < n; ++i) {
            let t = heights[i];
            for(; sp >= 0; --sp) {
                let h = heights[ pos[sp] ];
                if(h < t) {
                    break;
                }
                let b = sp ? pos[sp - 1] : -1;
                ans = max(ans, h * (i - 1 - b));
            }
            ++sp;
            pos[sp] = i;
        }
        return ans;
    }
};

struct IoBooster {
    IoBooster() {
        ios::sync_with_stdio(0);
        cin.tie(0);
    }
}iob;

理解不同编程语言版本的解决方案需要一些基础知识。以下是针对不同版本的详细介绍：

Go 版本：

Slice（切片）：Go 中的切片是动态数组，类似于其他语言中的数组或列表。了解如何声明、初始化和操作切片是编写 Go 代码的基本要求。
栈（Stack）：Go 版本使用一个切片来模拟栈的数据结构，实现了单调栈的功能。了解栈的基本操作，如入栈、出栈以及栈的初始化和访问方式。
闭包（Closure）：Go 版本使用了匿名函数（闭包）来定义一个用于获取某个位置的高度的函数。了解如何创建和使用闭包在这个解决方案中非常有帮助。
哨兵节点（Sentinel Node）：了解在算法中使用哨兵节点的目的，以及如何在 Go 中将哨兵节点添加到切片中。
循环：理解 Go 中的 for 循环，以及如何使用循环迭代数组和切片中的元素。
条件语句和算术运算符：理解 Go 中的条件语句（如 if）和算术运算符（如 +、-、* 等），以便计算矩形的面积。

Python 版本：

列表（List）：Python 中的列表类似于动态数组，用于存储一系列的元素。了解如何创建、操作和访问列表。
栈（Stack）：Python 版本使用一个列表来模拟栈的数据结构，实现了单调栈的功能。了解栈的基本操作，如入栈、出栈以及栈的初始化和访问方式。
条件语句和算术运算符：理解 Python 中的条件语句（如 if）和算术运算符（如 +、-、* 等），以便计算矩形的面积。
类和方法：Python 版本使用了类和方法，包括 __init__ 初始化方法和 largestRectangleArea 方法。了解如何定义和使用类及其方法。
列表迭代：了解如何使用 for 循环迭代列表中的元素，以及如何获取元素的索引和值。
条件表达式（List Comprehension）：Python 版本使用列表推导来计算最大面积。了解列表推导的基本语法。

Java 版本：

数组（Array）：Java 中的数组用于存储一系列的元素。了解如何声明、初始化和操作数组是 Java 编程的基础知识。
栈（Stack）：Java 版本使用数组来模拟栈的数据结构，实现了单调栈的功能。了解栈的基本操作，如入栈、出栈以及栈的初始化和访问方式。
循环：理解 Java 中的 for 循环，以及如何使用循环迭代数组和数组中的元素。
条件语句和算术运算符：理解 Java 中的条件语句（如 if）和算术运算符（如 +、-、* 等），以便计算矩形的面积。
类和方法：Java 版本使用了类和方法，包括 largestRectangleArea 方法。了解如何定义和使用类及其方法。
数组索引和长度：了解如何访问数组元素的索引和获取数组的长度。

C++ 版本：

数组（Array）：C++ 中的数组用于存储一系列的元素。了解如何声明、初始化和操作数组是 C++ 编程的基础知识。
栈（Stack）：C++ 版本使用数组来模拟栈的数据结构，实现了单调栈的功能。了解栈的基本操作，如入栈、出栈以及栈的初始化和访问方式。
条件语句和算术运算符：理解 C++ 中的条件语句（如 if）和算术运算符（如 +、-、* 等），以便计算矩形的面积。
数组索引和长度：了解如何访问数组元素的索引和获取数组的长度。
类和方法：C++ 版本使用了类和方法，包括 largestRectangleArea 方法。了解如何定义和使用类及其方法。
算法设计：理解如何设计算法来解决问题，包括使用栈数据结构来查找最大矩形的面积。

Go-Python-Java-C-LeetCode高分解法-第十二周合集

前言

文章目录

78. Subsets

题目

题目大意

解题思路

代码

Go

Python

Java

Cpp

79. Word Search

题目

题目大意

解题思路

代码

Go

Python

Java

Cpp

80. Remove Duplicates from Sorted Array II

题目

题目大意

解题思路

代码

Go

Python

Java

Cpp

81. Search in Rotated Sorted Array II

题目

题目大意

解题思路

代码

Go

Python

Java

Cpp

82. Remove Duplicates from Sorted List II

题目

题目大意

解题思路

代码

Go

Python

Java

Cpp

83. Remove Duplicates from Sorted List

题目

题目大意

解题思路

代码

Go

Python

Java

Cpp

84. Largest Rectangle in Histogram

题目

题目大意

解题思路

代码

Go

Python

Java

Cpp

你可能感兴趣的:(LeetCode,golang,python,java,c++,leetcode)