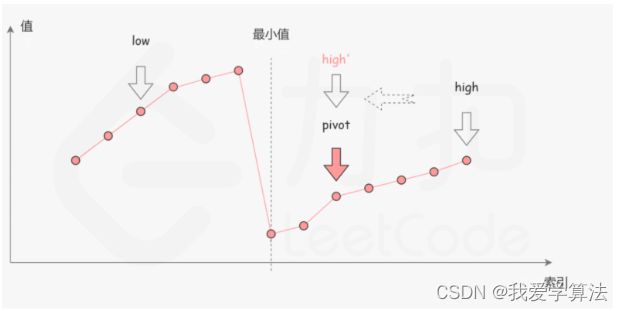
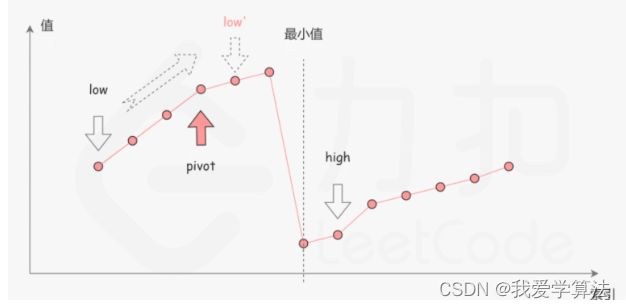
- 机器学习中的梯度到底是什么?(chat-gpt问答)
湫怿
机器学习gpt人工智能梯度
1、梯度是对损失函数求导吗?是的,梯度是对损失函数(或目标函数)求导数值化后的结果。梯度告诉我们目标函数在某个点上的方向性和变化率,这些信息是优化算法推进参数评估和更新的重要指标。在机器学习中,我们通过不断调整参数,使目标函数达到最小值,从而实现模型的训练和学习。2、为什么梯度要求偏导来求解?梯度是一个向量,它的方向指向函数值增加最快的方向,其大小表示函数值的变化率。为了确定梯度的方向和大小,需要
- 计算机视觉算法实战——驾驶员玩手机检测(主页有源码)
喵了个AI
计算机视觉实战项目计算机视觉算法智能手机
✨个人主页欢迎您的访问✨期待您的三连✨✨个人主页欢迎您的访问✨期待您的三连✨✨个人主页欢迎您的访问✨期待您的三连✨1.领域简介:玩手机检测的重要性与技术挑战驾驶员玩手机检测是智能交通安全领域的核心课题。根据NHTSA数据,美国每年因手机使用导致的交通事故超过3000起,中国公安部的统计显示开车使用手机的事故率是正常驾驶的23倍。该技术通过实时监测驾驶员手部动作和视线方向,识别非法使用手机行为,在以
- 深入解析 React Diff 算法:原理、优化与实践
赵大仁
前端技术jsreact.js前端前端框架
深入解析ReactDiff算法:原理、优化与实践1.引言React作为前端领域的标杆框架,采用虚拟DOM(VirtualDOM)来提升UI更新性能。React的Diff算法(Reconciliation)是虚拟DOM运行机制的核心,它决定了如何高效地对比新旧DOM并执行最少的操作来更新UI。本篇文章将深入探讨ReactDiff算法的原理、优化策略,并通过生动的示例解析其工作方式,让你能够更直观地理
- Java基础编程 找素数
是盈盈啊
笔记
说明:除了1和它本身以外,不能被其他正整数整除,就叫素数。方法是否需要接收数据进行处理?需要接收101以及200,以便找该区间中的素数。方法是否需要返回数据?需要返回找到的素数个数。方法内部的实现逻辑:使用for循环来产生如101到200之间的每个数;每拿到一个数,判断该数是否是素数;判断规则是:从2开始遍历到该数的一半的数据,看是否有数据可以整除它,有则不是素数,没有则是素数;根据判
- 深入浅出C++ STL:统领STL全局
有梦想的电信狗
《C++语法精粹》——c++stl数据结构算法开发语言idevisualstudio
深入浅出C++STL:统领STL全局深入浅出C++STL:统领STL全局github主页地址前言一、STL的前世今生1.1什么是STL?1.2STL版本演进二、STL六大核心组件详解2.1容器(Containers)容器性能对照表2.2算法(Algorithms)2.3迭代器(Iterators)2.4仿函数(Functors)2.5适配器(Adapters)2.6空间配置器(Allocators
- 静态顺序表
有梦想的电信狗
《数据结构与算法》数据结构c语言c++链表
顺序表顺序表和链表都是线性表的一种,此处介绍顺序表数据的存储结构有分为逻辑存储结构和物理存储结构。顺序表和链表(之后的文章会详解)实际上都是线性表,是因为他们的逻辑存储关系都是线性的,只是因为在计算机内存中存储的方式(物理存储结构)不同。两种物理存储结构各有优劣,作为开发者,在不同的场景需要灵活选用相应的数据结构来存储数据,来促使我们的程序更高效的运行。静态顺序表静态顺序表,顾名思义,即为顺序表的
- 机器学习中的梯度下降是什么意思?
yuanpan
机器学习人工智能
梯度下降(GradientDescent)是机器学习中一种常用的优化算法,用于最小化损失函数(LossFunction)。通过迭代调整模型参数,梯度下降帮助模型逐步逼近最优解,从而提升模型的性能。1.核心思想梯度下降的核心思想是利用损失函数的梯度(即导数)来指导参数的更新方向。具体来说:梯度:梯度是损失函数对模型参数的偏导数,表示损失函数在当前参数点上的变化率。下降:通过沿着梯度的反方向(即损失函
- c++模板初阶
晚安,cheems
c++开发语言
1.泛型编程泛型编程是一种编程范式,它允许程序员在编写代码时定义算法和数据结构时可以处理不同类型的数据,而不必为每种数据类型编写特定的代码。泛型编程的主要目的是提高代码的复用性、灵活性和可维护性。以下是一些关于泛型编程的基本概念:泛型的优点代码复用:同一套代码可以用于不同的数据类型。类型安全:在编译时就能检查出错误,而不是在运行时。性能:由于不需要进行类型转换,可以生成更高效的代码。泛型编程的例子
- CIR-DFENet:结合跨模态图像表示和双流特征增强网络进行活动识别
是Dream呀
神经网络计算机视觉人工智能神经网络深度学习
前言:零基础学Python:Python从0到100最新最全教程。想做这件事情很久了,这次我更新了自己所写过的所有博客,汇集成了Python从0到100,共一百节课,帮助大家一个月时间里从零基础到学习Python基础语法、Python爬虫、Web开发、计算机视觉、机器学习、神经网络以及人工智能相关知识,成为学业升学和求职工作的先行者!【优惠信息】•新专栏订阅前200名享9.9元优惠•订阅量破200
- JAVA面试_进阶部分_正确使用 Volatile 变量
茂茂在长安
JAVAjava面试开发语言
Java语言中的volatile变量可以被看作是一种“程度较轻的synchronized”;与synchronized块相比,volatile变量所需的编码较少,并且运行时开销也较少,但是它所能实现的功能也仅是synchronized的一部分。本文介绍了几种有效使用volatile变量的模式,并强调了几种不适合使用volatile变量的情形。锁提供了两种主要特性:互斥(mutualexclusio
- JAVA面试_进阶部分_混杂(1)
茂茂在长安
JAVAjava面试开发语言
1、说说线程安全问题,什么是线程安全,如何实现线程安全;线程安全-如果线程执行过程中不会产生共享资源的冲突,则线程安全。线程不安全-如果有多个线程同时在操作主内存中的变量,则线程不安全实现线程安全的三种方式1)互斥同步临界区:syncronized、ReentrantLock信号量semaphore互斥量mutex2)非阻塞同步CAS(CompareAndSwap)3)无同步方案可重入代码使用Th
- JAVA面试常见题_基础部分_springboot面试题
茂茂在长安
JAVAjava面试springboot
问题一什么是SpringBoot?多年来,随着新功能的增加,spring变得越来越复杂。只需访问https://spring.io/projects页面,我们就会看到可以在我们的应用程序中使用的所有Spring项目的不同功能。如果必须启动一个新的Spring项目,我们必须添加构建路径或添加Maven依赖关系,配置应用程序服务器,添加spring配置。因此,开始一个新的spring项目需要很多努力,
- 动态路由RIP的总结
nihuhui666
网络智能路由器RIP
动态路由所有路由器运行相同的路由协议,之后通过路由器之间的沟通,协商计算到达未知网段的路由信息静态路由优点:1.选路由管理员选择,更好掌控2.路由器资源占用更少3.静态路由相对动态路由更加安全缺点:1.配置量大2.静态路由无法根据网络拓扑结构的变化而变化—收敛动态路由:缺点:1.通过单一算法计算出来的路径,可能出现选路不佳2.资源占用多3.没有静态路由安全优点:1.配置量少2.动态路由可以根据网络
- OSPF总结
nihuhui666
网络ospf网络协议
OSPF–开放式最短路径优先协议1.选路–应为ospf是链路状态协议,收集拓扑信息之后将图形结构通过SPF算法转化为树形结构,计算出的路径不会有环路,并且以带宽作为开销的评判标准,所以OSPF选路优于rip2.收敛–因为OSPF的计数器短与rip,所以收敛快3.占用资源–从单一数据包角度来说,因为rip传递的是路由信息,所以资源占用不大而ospf传递拓扑信息,从单个数据包角度说,大于rip.但是o
- Java全栈开发学习路线:从基础到实战,掌握前后端与数据库,成为全栈软件工程师
软件职业规划
javajava
1.Java基础Java语法:变量、数据类型、运算符、控制流程(if、switch、循环等)面向对象编程(OOP):类与对象、继承、多态、封装、抽象类、接口异常处理:try-catch-finally、自定义异常集合框架:List、Set、Map、ArrayList、LinkedList、HashMap等泛型:泛型类、泛型方法、泛型接口IO流:文件读写、字节流、字符流多线程:线程创建、同步、锁、线
- 算法在各领域的广泛应用:100 个实例全解析
软件职业规划
AI&模型算法
一、互联网与信息技术领域搜索引擎算法:如谷歌的PageRank算法,用于根据网页的重要性和相关性对搜索结果进行排序,帮助用户快速找到所需信息。推荐系统算法:例如亚马逊和Netflix使用的协同过滤算法。根据用户的历史行为(购买、观看记录等)和其他相似用户的偏好,为用户推荐可能感兴趣的产品或内容。社交网络分析算法:用于分析社交网络中的用户关系,如Facebook通过算法发现用户的好友推荐、社区划分等
- 从零基础开始实现一个Spring Boot + Vue 项目的详细步骤指南
软件职业规划
springspringbootvue.js后端
一、准备工作1.开发环境搭建安装JDK(JavaDevelopmentKit):前往Oracle官网(https://www.oracle.com/java/technologies/javase-jdk11-downloads.html,以JDK11为例)下载适合你操作系统的JDK安装包,按照安装向导完成安装。安装完成后,配置系统环境变量,确保在命令行中能通过java-version命令查看到正
- 后端Web开发框架(Java)
测试人子期
软件测试测试开发java前端spring
SpringBoot是由Pivotal团队提供的全新框架,其设计目的是用来简化新Spring应用的初始搭建以及开发过程。该框架使用了特定的方式来进行配置,从而使开发人员不再需要定义样板化的配置。讲的通俗一点就是SpringBoot并不是一个新的框架,它只是整合和默认实现了很多框架的配置方式。通过SpringBoot,可以轻松地创建独立的、基于生产级别的基于Spring的应用程序。为什么使用Spri
- 不多 bb,直接来看Java 全栈面试进阶宝典,保底拿下offer
Java程序V
Javajava面试jvm
大家都知道,现在的Java面试是越来越难了!主要原因无非是两个:随着Java这个行业的兴起,不管是在家待业的、对自己现在工作不满意的、大学选错专业的、缺钱的、想自己学的等等这些人绝大部分都是选择了去学习Java!大量人才涌入,导致岗位竞争越来越大,面试也就越来越难!另外一个就是这两年的疫情影响,很多公司都宣布倒闭、裁员。加上互联网行业内卷的推动,面试造火箭工作拧螺丝已经是一个很常见的现象了!最近也
- 算法训练-拓扑排序2
往往歌咏理想
算法深度优先
洛谷P1807最长路https://www.luogu.com.cn/problem/P1807本题数据范围过大盲目使用dfs容易超时爆栈题目要求中提到i#defineintlonglong#defineendl'\n'/*===\\================//\\===================//\\============//\\==========//=========\\=
- 代码随想录算法训练营DAY05之栈和队列
失序空间
跟着代码随想录学算法算法c++
题目和链接232.用栈实现队列225.用队列实现栈20.有效的括号1047.删除字符串中的所有相邻重复项150.逆波兰表达式求值239.滑动窗口最大值347.前k个高频元素232.用栈实现队列题意:请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):实现MyQueue类:voidpush(intx)将元素x推到队列的末尾intpop()从
- Maven中的依赖管理: <dependencies>与<dependencyManagement>的区别
Fhoro
mavenjavaspringboot后端
在Java项目的构建过程中,依赖管理是一个至关重要的部分,特别是当使用Maven作为构建工具时。Maven提供了多种方式来管理项目的依赖,而和是最常用的两个概念。本文将详细探讨这两者的区别及其应用场景。什么是?dependencies是Maven项目中直接声明所需依赖的方式。在pom.xml文件中,我们可以通过标签列出项目所需的所有库和组件。每个依赖项都包括groupId、artifactId和v
- 2024前端Webpack面试题
司宁
前端面试题前端webpack
1、谈谈你对Webpack的理解Webpack是一个模块打包工具,可以使用它管理项目中的模块依赖,并编译输出模块所需的静态文件。它可以很好地管理、打包开发中所用到的HTML,CSS,JavaScript和静态文件(图片,字体)等,让开发更高效。对于不同类型的依赖,Webpack有对应的模块加载器,而且会分析模块间的依赖关系,最后合并生成优化的静态资源。2、Webpack的基本功能代码转换:Type
- 用Python打造智能家居安防系统,让科技守护你的家
Echo_Wish
Python笔记Python算法python智能家居科技
友友们好!我是Echo_Wish,我的的新专栏《Python进阶》以及《Python!实战!》正式启动啦!这是专为那些渴望提升Python技能的朋友们量身打造的专栏,无论你是已经有一定基础的开发者,还是希望深入挖掘Python潜力的爱好者,这里都将是你不可错过的宝藏。在这个专栏中,你将会找到:●深入解析:每一篇文章都将深入剖析Python的高级概念和应用,包括但不限于数据分析、机器学习、Web开发
- Java Spring Boot 常用技术及核心注解
微笑的曙光(StevenLi)
JAVAjavaspringboot开发语言
一、常用技术自动配置(Auto-Configuration)SpringBoot根据类路径中的依赖自动配置应用程序。例如,引入spring-boot-starter-web会自动配置内嵌Tomcat和SpringMVC。@EnableAutoConfiguration//启用自动配置起步依赖(StarterDependencies)通过预定义的依赖集合(如spring-boot-starter-d
- 《Operating System Concepts》阅读笔记:p309-p330
操作系统
《OperatingSystemConcepts》学习第29天,p309-p330总结,总计22页。一、技术总结1.Python中的并发编程(1)semaphoreclassthreading.Semaphore(value=1)。(2)conditionvariableclassthreading.Condition(lock=None)书上使用的是Java,因本人在开发工作中使用的是Pytho
- fetch java_拦截Java语言中的Fetch()API响应和请求
就大概是这样
fetchjava
我想拦截Javascript中的提取API请求和响应。例如:在发送请求之前,要拦截请求URL,一旦获得响应,就要拦截响应。以下代码用于拦截所有XMLHTTPRequest的响应。(function(open){XMLHttpRequest.prototype.open=function(XMLHttpRequest){varself=this;this.addEventListener("read
- XMLHttpRequest、Fetch、Axios和AJAX的关系
冰镇屎壳郎
前端#JavaScriptajax前端javascript
一、基于http协议用于前后端通信的工具1、XMLHttpRequest(原生JS对象)XMLHttpRequest(XHR)是原生JavaScript对象。通过XMLHttpRequest可以在不刷新页面的情况下请求特定URL,获取数据。特性:浏览器广泛支持功能丰富:可以跟踪请求的状态、支持进度事件、文件上传、同步请求等可同步可异步不支持PromiseAPI2、Fetch(浏览器原生API)(1
- JVM汇总篇
xk_一步一步来
JVMJVM汇总篇
转自:https://blog.csdn.net/wolf_love666/article/details/85712922书中内容来自于深入理解java虚拟机,作者周志明。会融合自己的知识和理解来记录下来,为了赚钱而奋斗!DayDayUp!!!前期准备:准备篇(一)内存管理内存如何划分、内存溢出的原因----点击这里内存分配和垃圾回收-----点击这里(二)虚拟机如何执行数据存储和访问(类文件结
- 通过覆盖原型属性拦截 XMLHttpRequest 响应
@大迁世界
服务器运维
在JavaScript中有两种发起HTTP请求的API-现代的fetch()和传统的XMLHttpRequest。它们功能完全相同,只是语法不同。XMLHttpRequest使用回调处理响应,而fetch()返回更方便使用的Promise。XMLHttpRequest是发起HTTP请求的主流API。在新项目中使用传统的XMLHttpRequest是没有意义的。另一方面,将现有可运行的基于XMLHt
- eclipse maven
IXHONG
eclipse
eclipse中使用maven插件的时候,运行run as maven build的时候报错
-Dmaven.multiModuleProjectDirectory system propery is not set. Check $M2_HOME environment variable and mvn script match.
可以设一个环境变量M2_HOME指
- timer cancel方法的一个小实例
alleni123
多线程timer
package com.lj.timer;
import java.util.Date;
import java.util.Timer;
import java.util.TimerTask;
public class MyTimer extends TimerTask
{
private int a;
private Timer timer;
pub
- MySQL数据库在Linux下的安装
ducklsl
mysql
1.建好一个专门放置MySQL的目录
/mysql/db数据库目录
/mysql/data数据库数据文件目录
2.配置用户,添加专门的MySQL管理用户
>groupadd mysql ----添加用户组
>useradd -g mysql mysql ----在mysql用户组中添加一个mysql用户
3.配置,生成并安装MySQL
>cmake -D
- spring------>>cvc-elt.1: Cannot find the declaration of element
Array_06
springbean
将--------
<?xml version="1.0" encoding="UTF-8"?>
<beans xmlns="http://www.springframework.org/schema/beans"
xmlns:xsi="http://www.w3
- maven发布第三方jar的一些问题
cugfy
maven
maven中发布 第三方jar到nexus仓库使用的是 deploy:deploy-file命令
有许多参数,具体可查看
http://maven.apache.org/plugins/maven-deploy-plugin/deploy-file-mojo.html
以下是一个例子:
mvn deploy:deploy-file -DgroupId=xpp3
- MYSQL下载及安装
357029540
mysql
好久没有去安装过MYSQL,今天自己在安装完MYSQL过后用navicat for mysql去厕测试链接的时候出现了10061的问题,因为的的MYSQL是最新版本为5.6.24,所以下载的文件夹里没有my.ini文件,所以在网上找了很多方法还是没有找到怎么解决问题,最后看到了一篇百度经验里有这个的介绍,按照其步骤也完成了安装,在这里给大家分享下这个链接的地址
- ios TableView cell的布局
张亚雄
tableview
cell.imageView.image = [UIImage imageNamed:[imageArray objectAtIndex:[indexPath row]]];
CGSize itemSize = CGSizeMake(60, 50);
&nbs
- Java编码转义
adminjun
java编码转义
import java.io.UnsupportedEncodingException;
/**
* 转换字符串的编码
*/
public class ChangeCharset {
/** 7位ASCII字符,也叫作ISO646-US、Unicode字符集的基本拉丁块 */
public static final Strin
- Tomcat 配置和spring
aijuans
spring
简介
Tomcat启动时,先找系统变量CATALINA_BASE,如果没有,则找CATALINA_HOME。然后找这个变量所指的目录下的conf文件夹,从中读取配置文件。最重要的配置文件:server.xml 。要配置tomcat,基本上了解server.xml,context.xml和web.xml。
Server.xml -- tomcat主
- Java打印当前目录下的所有子目录和文件
ayaoxinchao
递归File
其实这个没啥技术含量,大湿们不要操笑哦,只是做一个简单的记录,简单用了一下递归算法。
import java.io.File;
/**
* @author Perlin
* @date 2014-6-30
*/
public class PrintDirectory {
public static void printDirectory(File f
- linux安装mysql出现libs报冲突解决
BigBird2012
linux
linux安装mysql出现libs报冲突解决
安装mysql出现
file /usr/share/mysql/ukrainian/errmsg.sys from install of MySQL-server-5.5.33-1.linux2.6.i386 conflicts with file from package mysql-libs-5.1.61-4.el6.i686
- jedis连接池使用实例
bijian1013
redisjedis连接池jedis
实例代码:
package com.bijian.study;
import java.util.ArrayList;
import java.util.List;
import redis.clients.jedis.Jedis;
import redis.clients.jedis.JedisPool;
import redis.clients.jedis.JedisPoo
- 关于朋友
bingyingao
朋友兴趣爱好维持
成为朋友的必要条件:
志相同,道不合,可以成为朋友。譬如马云、周星驰一个是商人,一个是影星,可谓道不同,但都很有梦想,都要在各自领域里做到最好,当他们遇到一起,互相欣赏,可以畅谈两个小时。
志不同,道相合,也可以成为朋友。譬如有时候看到两个一个成绩很好每次考试争做第一,一个成绩很差的同学是好朋友。他们志向不相同,但他
- 【Spark七十九】Spark RDD API一
bit1129
spark
aggregate
package spark.examples.rddapi
import org.apache.spark.{SparkConf, SparkContext}
//测试RDD的aggregate方法
object AggregateTest {
def main(args: Array[String]) {
val conf = new Spar
- ktap 0.1 released
bookjovi
kerneltracing
Dear,
I'm pleased to announce that ktap release v0.1, this is the first official
release of ktap project, it is expected that this release is not fully
functional or very stable and we welcome bu
- 能保存Properties文件注释的Properties工具类
BrokenDreams
properties
今天遇到一个小需求:由于java.util.Properties读取属性文件时会忽略注释,当写回去的时候,注释都没了。恰好一个项目中的配置文件会在部署后被某个Java程序修改一下,但修改了之后注释全没了,可能会给以后的参数调整带来困难。所以要解决这个问题。
&nb
- 读《研磨设计模式》-代码笔记-外观模式-Facade
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
/*
* 百度百科的定义:
* Facade(外观)模式为子系统中的各类(或结构与方法)提供一个简明一致的界面,
* 隐藏子系统的复杂性,使子系统更加容易使用。他是为子系统中的一组接口所提供的一个一致的界面
*
* 可简单地
- After Effects教程收集
cherishLC
After Effects
1、中文入门
http://study.163.com/course/courseMain.htm?courseId=730009
2、videocopilot英文入门教程(中文字幕)
http://www.youku.com/playlist_show/id_17893193.html
英文原址:
http://www.videocopilot.net/basic/
素
- Linux Apache 安装过程
crabdave
apache
Linux Apache 安装过程
下载新版本:
apr-1.4.2.tar.gz(下载网站:http://apr.apache.org/download.cgi)
apr-util-1.3.9.tar.gz(下载网站:http://apr.apache.org/download.cgi)
httpd-2.2.15.tar.gz(下载网站:http://httpd.apac
- Shell学习 之 变量赋值和引用
daizj
shell变量引用赋值
本文转自:http://www.cnblogs.com/papam/articles/1548679.html
Shell编程中,使用变量无需事先声明,同时变量名的命名须遵循如下规则:
首个字符必须为字母(a-z,A-Z)
中间不能有空格,可以使用下划线(_)
不能使用标点符号
不能使用bash里的关键字(可用help命令查看保留关键字)
需要给变量赋值时,可以这么写:
- Java SE 第一讲(Java SE入门、JDK的下载与安装、第一个Java程序、Java程序的编译与执行)
dcj3sjt126com
javajdk
Java SE 第一讲:
Java SE:Java Standard Edition
Java ME: Java Mobile Edition
Java EE:Java Enterprise Edition
Java是由Sun公司推出的(今年初被Oracle公司收购)。
收购价格:74亿美金
J2SE、J2ME、J2EE
JDK:Java Development
- YII给用户登录加上验证码
dcj3sjt126com
yii
1、在SiteController中添加如下代码:
/**
* Declares class-based actions.
*/
public function actions() {
return array(
// captcha action renders the CAPTCHA image displ
- Lucene使用说明
dyy_gusi
Lucenesearch分词器
Lucene使用说明
1、lucene简介
1.1、什么是lucene
Lucene是一个全文搜索框架,而不是应用产品。因此它并不像baidu或者googleDesktop那种拿来就能用,它只是提供了一种工具让你能实现这些产品和功能。
1.2、lucene能做什么
要回答这个问题,先要了解lucene的本质。实际
- 学习编程并不难,做到以下几点即可!
gcq511120594
数据结构编程算法
不论你是想自己设计游戏,还是开发iPhone或安卓手机上的应用,还是仅仅为了娱乐,学习编程语言都是一条必经之路。编程语言种类繁多,用途各 异,然而一旦掌握其中之一,其他的也就迎刃而解。作为初学者,你可能要先从Java或HTML开始学,一旦掌握了一门编程语言,你就发挥无穷的想象,开发 各种神奇的软件啦。
1、确定目标
学习编程语言既充满乐趣,又充满挑战。有些花费多年时间学习一门编程语言的大学生到
- Java面试十问之三:Java与C++内存回收机制的差别
HNUlanwei
javaC++finalize()堆栈内存回收
大家知道, Java 除了那 8 种基本类型以外,其他都是对象类型(又称为引用类型)的数据。 JVM 会把程序创建的对象存放在堆空间中,那什么又是堆空间呢?其实,堆( Heap)是一个运行时的数据存储区,从它可以分配大小各异的空间。一般,运行时的数据存储区有堆( Heap)和堆栈( Stack),所以要先看它们里面可以分配哪些类型的对象实体,然后才知道如何均衡使用这两种存储区。一般来说,栈中存放的
- 第二章 Nginx+Lua开发入门
jinnianshilongnian
nginxlua
Nginx入门
本文目的是学习Nginx+Lua开发,对于Nginx基本知识可以参考如下文章:
nginx启动、关闭、重启
http://www.cnblogs.com/derekchen/archive/2011/02/17/1957209.html
agentzh 的 Nginx 教程
http://openresty.org/download/agentzh-nginx-tutor
- MongoDB windows安装 基本命令
liyonghui160com
windows安装
安装目录:
D:\MongoDB\
新建目录
D:\MongoDB\data\db
4.启动进城:
cd D:\MongoDB\bin
mongod -dbpath D:\MongoDB\data\db
&n
- Linux下通过源码编译安装程序
pda158
linux
一、程序的组成部分 Linux下程序大都是由以下几部分组成: 二进制文件:也就是可以运行的程序文件 库文件:就是通常我们见到的lib目录下的文件 配置文件:这个不必多说,都知道 帮助文档:通常是我们在linux下用man命令查看的命令的文档
二、linux下程序的存放目录 linux程序的存放目录大致有三个地方: /etc, /b
- WEB开发编程的职业生涯4个阶段
shw3588
编程Web工作生活
觉得自己什么都会
2007年从学校毕业,凭借自己原创的ASP毕业设计,以为自己很厉害似的,信心满满去东莞找工作,找面试成功率确实很高,只是工资不高,但依旧无法磨灭那过分的自信,那时候什么考勤系统、什么OA系统、什么ERP,什么都觉得有信心,这样的生涯大概持续了约一年。
根本不是自己想的那样
2008年开始接触很多工作相关的东西,发现太多东西自己根本不会,都需要去学,不管是asp还是js,
- 遭遇jsonp同域下变作post请求的坑
vb2005xu
jsonp同域post
今天迁移一个站点时遇到一个坑爹问题,同一个jsonp接口在跨域时都能调用成功,但是在同域下调用虽然成功,但是数据却有问题. 此处贴出我的后端代码片段
$mi_id = htmlspecialchars(trim($_GET['mi_id ']));
$mi_cv = htmlspecialchars(trim($_GET['mi_cv ']));
贴出我前端代码片段:
$.aj