CSAPP - CacheLab
CSAPP - CacheLab
- 本实验上学期花了一周的时间才做完，也算是CSAPP中做的最认真的一个了
- 相比于PhaseA，PhaseB更加的阴间和耗时
- 在做实验的过程中参考了知乎大佬和CSDN上的代码，并融入了自己的idea，希望能帮助到计软的同学（笑）
PhaseA
实验要求
- 实现一个cache模拟器，运行时输入s,b,E，要求统计命中，未命中和驱逐的次数，cache忽略块偏移量，且采用LRU策略进行驱逐
实验过程
- traces文件中包含I，L，S，M四种模式：I需要忽略，而经过分析可知S（Store）和L（Load）模式本质上相同（缓存中已存在直接命中，缓存中未存在则未命中，如果缓存已满则需要驱逐），而M模式则是先进行L再进行S模式
声明cache_line结构体
struct cache_line
{
int tag; //标记位
int LRU_counter; //最后访问时间
};
- cache_line中包含tag标记位和LRU_counter用于记录最后访问时间便于驱逐（Valid_bit有效位省略而采用另一种方法）
建立全局变量
struct cache_line **cache;
int hit_count, miss_count, eviction_count;
int *cache_index;
int s, E, b, S;
int count = 0; //时间刻
- cache结构体二级指针用于建立二维数组
- hit_count，miss_count，eviction_count用于记录命中，未命中和驱逐的次数
- cache_index以及指针用于建立一维数组来维护组有效行的个数
- s，E，b接收传入参数，S便于开辟内存
- count作为时间刻
接收传入s，E，b参数
int opt;
char *trace_name; //trace文件地址
//命令行读入
while ((opt = getopt(argc, argv, "s:E:b:t:")) != -1)
{
switch (opt)
{
case 's':
s = atoi(optarg); //读入s
break;
case 'E':
E = atoi(optarg); //读入E
break;
case 'b':
b = atoi(optarg); //读入b
break;
case 't':
trace_name = optarg; //读入地址
default:
break;
}
}
- 使用getopt函数将参数传入s，E，b中，同时创建trace_name字符串用于记录trace文件的地址便于之后文件的读入
初始化数组
//初始化
S = pow(2, s); //计算S=2^s
cache = (struct cache_line **)malloc(sizeof(struct cache_line *) * S);
for (int i = 0; i < S; i++)
cache[i] = (struct cache_line *)malloc(sizeof(struct cache_line *) * E); //cache开辟内存
for (int i = 0; i < S; i++)
for (int j = 0; j < E; j++)
cache[i][j].tag = cache[i][j].LRU_counter = 0; //cache初始化
cache_index = (int *)malloc(sizeof(int) * S); //cache_index开辟内存
memset(cache_index, 0, sizeof(int) * S); //cache_index初始化
- 使用malloc函数对cache_line和cache_index开辟内存，建立cache_line[S][E]和cache[S]，同时初始化为0
（cache_line[x][y]表示第x组第y行所存内容，cache[x]表示第x组最后的有效块所在行数）
文件读入
//文件读入
FILE *pFile = fopen(trace_name, "r"); //打开文件
char identifier;
unsigned address;
int size;
- 使用fopen函数和之前读入的trace_name文件的地址读入*pFile中，并创建identifier，address，size用于存储文件中读入的内容
读入后数据处理
while (fscanf(pFile, " %c %x,%d", &identifier, &address, &size) > 0) //按行读入
{
if (identifier == 'I') //忽略I模式
continue;
int t_address = address / ((int)pow(2, s + b)); //计算标记位
int s_address = address / ((int)pow(2, b)) % (int)(pow(2, s)); //计算索引位
if (identifier == 'M') //M模式两次solve
{
Solve(t_address, s_address);
Solve(t_address, s_address);
}
else //S模式或L模式
Solve(t_address, s_address);
}
- 使用fscanf函数按行读取trace文件的内容，模式读入identifier中，地址读入address中，操作范围读入size中
- 由于忽略I模式，所以identifier==’I’后直接continue
- 由于忽略块偏移量，所以无需记录地址中的块偏移部分而只需统计索引部分（s_address）和标记部分（t_address）
- 根据读入的s和计算并分割出这两部分（t_address=⌊address / 2^(s+b) ⌋，
s_address=⌊address/ 2^b ⌋mod 2^s） - 由于L模式和S模式操作方式相同，而M模式是L模式+S模式，所以可以只写一个solve函数，对于M模式执行两次，而对于L和S模式都只执行一次
结束阶段
//结束
free(cache);
free(cache_index); //释放内存
fclose(pFile); //关闭文件
printSummary(hit_count, miss_count, eviction_count); //输出
- 释放开辟的内存并关闭文件
- 调用printSummary输出命中，未命中和驱逐的个数
solve函数
前提：同一个组内，有效块按访问时间顺序依次顺序存储（组未满状态下），且使用cache_index来记录该组最后的有效块所在行数
- 不论Store还是Load都存在两种状态：缓存中已存在——命中，缓存中不存在——未命中
- 1.命中状态（find_flag=1）
- 基本思想：在cache_index[组数]下标的范围内（该组所有有效块）寻找，如果找到则命中，并更新最后访问时间
int find_flag = 0; //寻找哨兵
for (int i = 0; i < cache_index[s_address]; i++)
{
if (cache[s_address][i].tag == t_address) //找到
{
++hit_count;
cache[s_address][i].LRU_counter = count;
find_flag = 1;
break;
}
}
-
- 不命中状态（find_flag=0）
- 基本思想：在该组所有有效行中都寻找不到，则未命中。此时分两种情况：
- 2.1. 组未满：
- 无需驱逐，仅需在cache[组数][]中向后插入该有效块，并更新最后访问时间和该组cache_line[]
if (cache_index[s_address] != E) //组未满 { ++miss_count; //未命中 cache[s_address][cache_index[s_address]].tag = t_address; //更新缓存 cache[s_address][cache_index[s_address]++].LRU_counter = count; //更新最后访问时间 }- 2.2. 组已满：
- 需要驱逐，此时在该组中寻找访问时间最小的有效块（LRU），驱逐替换该块，并更新该块最后访问时间
else //组已满，需要LRU { ++eviction_count; //驱逐 ++miss_count; //未命中 int min_count = cache[s_address][0].LRU_counter; //最后访问时间最远块访问时间 int min_count_index = 0; //最后访问时间最远块下标 for (int i = 1; i < E; i++) if (cache[s_address][i].LRU_counter < min_count) { min_count = cache[s_address][i].LRU_counter; //更新最后访问时间最远块访问时间 min_count_index = i; //更新最后访问时间最远块下标 } cache[s_address][min_count_index].tag = t_address; //更新缓存 cache[s_address][min_count_index].LRU_counter = count; //更新最后访问时间 } - 在solve函数结束后更新count时间刻，以便于下次使用更新访问时间
++count; //更新时间刻
完整代码
#include "cachelab.h"
#include PhaseB
实验要求
- 优化转置矩阵的代码，使其未命中率尽可能低
- 矩阵大小分别为32*32,64*64和61*67，由于不同矩阵大小的代码可能不同，所以所写代码只对测试的三组数据进行优化
- 从老师所给的PPT和pdf中可以知道对矩阵分组（blocking）可以有效地提升缓存命中率
前提：从导出的trans.f0文件中可以得知，使用./test-trans命令测试得出的未命中数量比实际的多3（valgrind模拟额外开销）
以下提及的所有未命中均为实际未命中数量，如需转换到命令输出需加3
32*32（理论最优256）
基准测试
- 经过测试，文件自带转置函数对于32*32矩阵转置未命中为1180
命中率分析
- A：（156未命中，15.23%未命中率）
-
- B：（1024未命中，100%未命中率）
- 在A矩阵遍历每一行时，B中每一列的每个元素每隔8行都会发生冲突不命中，如此造成低命中率
第一次优化
- 由于是每隔8行发生不命中，所以首先考虑8*8矩阵分块。注意到每个缓存块中正好能存放8个整型，且每个分块除对角线互不干扰（不会发生驱逐），如此一来按块进行转置，每个块中不会发生大量的冲突不命中，且块与块之间绝对不会发生冲突。所以8*8分块是可行的
- 代码
- 经过测试，8*8对于32*32矩阵转置未命中为340
命中率分析
-
A：（156未命中，15.23%未命中率）
-
B：（184未命中17.97%未命中率）
-
A没有发生变化而B命中率大大提高，但总未命中数仍然超过300
第二次优化
-
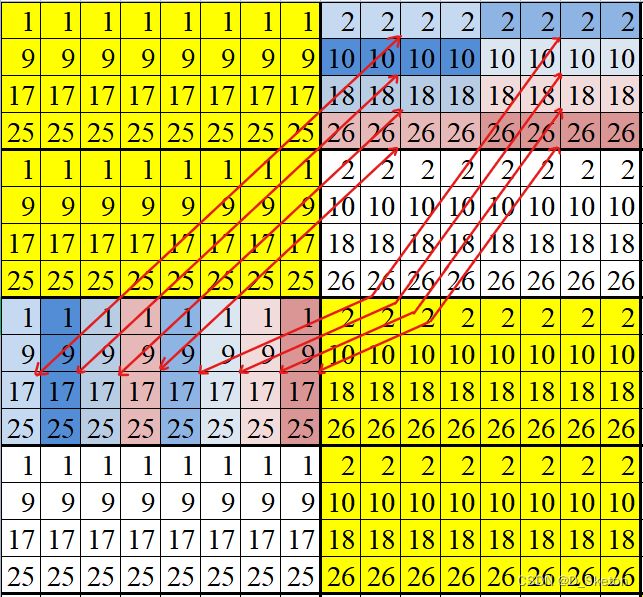
注意到A矩阵中元素仍然会和B矩阵中元素互相冲突，导致A矩阵的对角线和B矩阵对角线上一格元素发生冲突不命中，具体解释如图所示：
-
大部分冲突命中均发生在A和B的相邻操作中（红色画圈部分），所以可以考虑先同时对A块中的同一行进行读取操作，再同时对B块对应列进行写入操作，这样便可以消除相邻操作带来的冲突不命中
-
替换内部循环代码为：
-
经过测试，8*8对于32*32矩阵转置未命中为284，已达到满分标准
命中率分析
-
A：（128未命中，12.5%未命中率）
-
B：（156未命中，15.23%未命中率）
64*64（理论最优1024）
基准测试
- 相比于32*32矩阵缓存能存放8行元素，64*64矩阵缓存只能存放4行元素
- 首先尝试和上题一样8*8分块并一次性读取一行（代码省略）
- 经过测试，8*8并一次性读取对于64*64矩阵转置未命中为4608，几乎没有提升
- 文件自带转置函数未命中为4720
命中率分析
-
A：（512未命中，12.5%未命中率）
-
B：（4096未命中，100%未命中率）
-
由于每次对A一次性读取一行，所以A矩阵的命中率得到了提升（12.5%未命中率）
-
但由于缓存只能存下矩阵前4行元素，B矩阵在读取后4列时会覆盖前4列，同时读取前4列时会覆盖后4列，导致每个元素都发生了冲突不命中（初始为冷不命中）
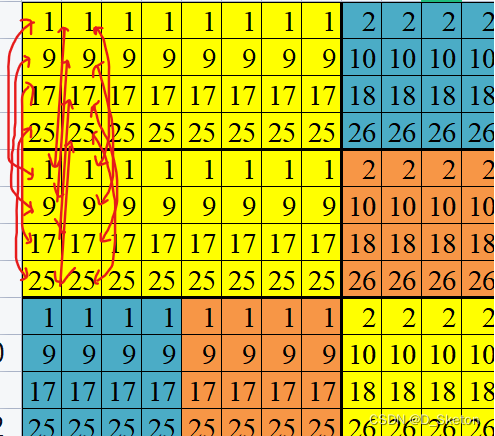
（红色箭头表示冲突不命中）
第一次优化
-
由于前后4列会互相覆盖，所以考虑将8*8分块改为4*4分块，每次一次性读取一行，这样便能降低B矩阵的未命中率
-
代码：
-
经过测试，4*4并一次性读取对于64*64矩阵转置未命中为1696，有了较大的提升，但依然没有小于1300
命中率分析
-
A：（576，14.06%未命中率）
-
B：（1120，27.34%未命中率）
-
B矩阵由于降低分块大小且仍然一次性读取一行，不再100%未命中率，但由于采用了4*4分块，在非对角线块内部仍然会发生大量冲突不命中，未命中率为25%，而在对角线块上由于A矩阵和B矩阵所映射到相同的缓存块，导致A矩阵和B矩阵发生冲突不命中，未命中率更高
（非对角线块）
- 由此可见单纯的4*4分块已经达到了极限，需要更进一步的优化
第二次优化
- 由于缓存中能存放8个整型，所以考虑先进行8*8分块，而在大块内部再进行4*4分块操作
为了最大化的利用缓存，尽可能低减少冲突，考虑在8*8大块内部进行三步操作：
这里的思想参考了某位大神，这里着重分析
每个8*8块中的4*4块按行顺序将块被标记为1,2,3,4块
-
1.首先对A矩阵的1,2块一次性读取一行8个元素，并按列分别移入B矩阵的1块和2块中
-
2.对A矩阵的3块按列读取，对B矩阵的2块按行读取，将读取到的A矩阵按行移入B矩阵的2块，将读取到的B矩阵按行移入B矩阵的3块（两次读取后直接进行移入）
-
3.对A矩阵的4块一次性读取两行，并按列移入B矩阵的4块中
-
代码：
-
经过测试，该方法对于64*64矩阵转置未命中为1160，已达到满分标准
命中率分析
-
A：（552，13.48%未命中率）
-
B：（608，14.84%未命中率）
-
对于对角块：
- 第一步对A矩阵的1,2块一次性读取一行8个元素，A矩阵的1,2块的未命中率降低为12.5%（本来为25%），由于充分使用了缓存块，提升了A矩阵命中率
- 对于B矩阵按列移入1,2块，在首次写入1块的第一列时冷不命中，同时缓存被写入相对应行中元素，所以2块所有元素在这一步中会全部命中，而仅仅会在1块的对角线上发生冲突不命中
- 第二步先对A矩阵的3块按列读取，对B矩阵的2块按行读取
- A矩阵首次读取3块第一列发生冲突不命中，而在之后的的读取中对角线上元素会和B矩阵发生冲突不命中，而对于B矩阵，由于按行进行读取，所以冲突不命中仅仅发生在2块的第一列上
- 将读取到的A矩阵按行移入B矩阵的2块，将读取到的B矩阵按行移入B矩阵的3块（注意行列顺序）
- 由于之前在读取时已按行将B矩阵存入缓存中，所以B矩阵2块上会全部命中，而仅仅在移入3块时在每一列上发生冲突不命中
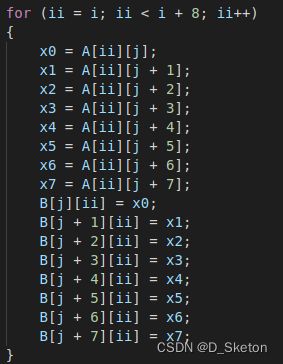
- 第三步对A矩阵的4块一次性读取两行，并按列移入B矩阵的4块中
- 和之前4*4分块类似，但选择一次性读入两行相比于一次性读取一行能小幅提升命中率
-
对于非对角块：
- 三步操作都仅仅会在4个小块的第一列上发生冲突不命中，未命中率均为12.5%，对于B矩阵来说命中率大大提升
61*67
- 由于61和67都是素数，无法被8整除，所以在缓存中会发生错位现
- 矩阵不是正方形，A矩阵和B矩阵的行数和列数并不相等，所以直接分析相比于之前会非常困难，且效率也不高，所以本情况不再详细分析
- 由于冲突不命中的概率相比于64*64会下降，所以块的大小可以适当加大，此外对于不能分块的区域需要分开处理
第一次优化
-
首先考虑和64*64矩阵一样的转置方法：
将61*67的56*64部分采用和之前一样的方法，而对于剩下的部分采用最原始的直接转置法：
-
经测试，未命中为2058，已经非常接近2000：
-
剩下的矩阵考虑分成3大部分：
-
第一部分（A[64][0]~A[67][59]）
-
分成3*6的块，每次一次性读取一行进行转置
-
第二部分（A[0][56]~A[63][59]）
-
一次性读取一行进行转置
-
第三部分（A[64][60]~A[66][60]）
-
直接转置
-
剩下部分的代码：（不完整）
-
经测试，未命中为1971，已达到了满分标准，但还有优化空间
第二次优化
-
经过测试，发现存在更优解：
-
将61*67的60*60部分分成20*4的块，每次一次性读取两行
-
剩下的矩阵考虑分成2大部分：
-
第一部分（A[0][60]~A[66][60]）
-
直接转置
-
第二部分（A[60][0]~A[66][59]）
-
一次性读取一列进行转置（非按行读取）
-
代码：
-
经测试，未命中为1750，有了较大幅度的优化，同时代码复杂度也大大下降
完整代码
void transpose_submit(int M, int N, int A[N][M], int B[M][N])
{
int i, j, ii;
int x0, x1, x2, x3, x4, x5, x6, x7;
if (M == 32) //32x32矩阵
{
for (i = 0; i < 32; i += 8)
for (j = 0; j < 32; j += 8) //8x8分块
for (ii = i; ii < i + 8; ii++)
{
x0 = A[ii][j]; x1 = A[ii][j + 1];
x2 = A[ii][j + 2]; x3 = A[ii][j + 3];
x4 = A[ii][j + 4]; x5 = A[ii][j + 5];
x6 = A[ii][j + 6]; x7 = A[ii][j + 7]; //每次一次性读取一行，存入x0~x7
B[j][ii] = x0; B[j + 1][ii] = x1;
B[j + 2][ii] = x2; B[j + 3][ii] = x3;
B[j + 4][ii] = x4; B[j + 5][ii] = x5;
B[j + 6][ii] = x6; B[j + 7][ii] = x7; //移入B矩阵
}
}
else if (M == 64) //64x64矩阵
{
for (i = 0; i < 64; i += 8)
for (j = 0; j < 64; j += 8) //先8x8分块
{
//8x8大块中进行3步操作
for (ii = i; ii < i + 4; ii++) //A矩阵的1,2块
{
x0 = A[ii][j]; x1 = A[ii][j + 1];
x2 = A[ii][j + 2]; x3 = A[ii][j + 3];
x4 = A[ii][j + 4]; x5 = A[ii][j + 5];
x6 = A[ii][j + 6]; x7 = A[ii][j + 7]; //一次性读取一行，存入x0~x7
B[j][ii] = x0; B[j + 1][ii] = x1;
B[j + 2][ii] = x2; B[j + 3][ii] = x3; //按列移入B矩阵1块
B[j][ii + 4] = x4; B[j + 1][ii + 4] = x5;
B[j + 2][ii + 4] = x6; B[j + 3][ii + 4] = x7; //按列移入B矩阵2块
}
for (ii = j; ii < j + 4; ii++) //A矩阵的3块和B矩阵的2块
{
x0 = A[i + 4][ii]; x1 = A[i + 5][ii];
x2 = A[i + 6][ii]; x3 = A[i + 7][ii]; //按列读取A矩阵3块
x4 = B[ii][i + 4]; x5 = B[ii][i + 5];
x6 = B[ii][i + 6]; x7 = B[ii][i + 7]; //按行读取B矩阵2块
B[ii][i + 4] = x0; B[ii][i + 5] = x1;
B[ii][i + 6] = x2; B[ii][i + 7] = x3; //按行移入B矩阵2块
B[ii + 4][i] = x4; B[ii + 4][i + 1] = x5;
B[ii + 4][i + 2] = x6; B[ii + 4][i + 3] = x7; //按行移入B矩阵3块
}
for (ii = i + 4; ii < i + 8; ii += 2) //A矩阵的4块
{
x0 = A[ii][j + 4]; x1 = A[ii][j + 5];
x2 = A[ii][j + 6]; x3 = A[ii][j + 7];
x4 = A[ii + 1][j + 4]; x5 = A[ii + 1][j + 5];
x6 = A[ii + 1][j + 6]; x7 = A[ii + 1][j + 7]; //一次性读取两行，存入x0~x7
B[j + 4][ii] = x0; B[j + 5][ii] = x1;
B[j + 6][ii] = x2; B[j + 7][ii] = x3;
B[j + 4][ii + 1] = x4; B[j + 5][ii + 1] = x5;
B[j + 6][ii + 1] = x6; B[j + 7][ii + 1] = x7; //移入B矩阵
}
}
}
else //61x67矩阵
{
//以下为1750miss方法
for (i = 0; i < 60; i += 20)
for (j = 0; j < 60; j += 4) //60x60部分进行20x4分块
for (ii = i; ii < i + 20; ii += 2)
{
x0 = A[ii][j]; x1 = A[ii][j + 1];
x2 = A[ii][j + 2]; x3 = A[ii][j + 3];
x4 = A[ii + 1][j]; x5 = A[ii + 1][j + 1];
x6 = A[ii + 1][j + 2]; x7 = A[ii + 1][j + 3]; //一次性读取两行，存入x0~x7
B[j][ii] = x0; B[j + 1][ii] = x1;
B[j + 2][ii] = x2; B[j + 3][ii] = x3;
B[j][ii + 1] = x4; B[j + 1][ii + 1] = x5;
B[j + 2][ii + 1] = x6; B[j + 3][ii + 1] = x7; //移入B矩阵
}
for (i = 0; i < 67; i++) //A[0][60]~A[66][60]部分直接转置
B[60][i] = A[i][60];
for (i = 0; i < 60; i++) //A[60][0]~A[66][59]部分
{
x0=A[60][i]; x1=A[61][i];
x2=A[62][i]; x3=A[63][i];
x4=A[64][i]; x5=A[65][i];
x6=A[66][i]; //一次性读取一列，存入x0~x6
B[i][60]=x0; B[i][61]=x1;
B[i][62]=x2; B[i][63]=x3;
B[i][64]=x4; B[i][65]=x5;
B[i][66]=x6; //移入B矩阵
}
/*
//以下为1971miss方法
for (i = 0; i < 64; i += 8)
for (j = 0; j < 56; j += 8) //64x56部分进行8x8分块
{
for (ii = i; ii < i + 4; ii++) //以下方法同64x64
{
x0 = A[ii][j]; x1 = A[ii][j + 1];
x2 = A[ii][j + 2]; x3 = A[ii][j + 3];
x4 = A[ii][j + 4]; x5 = A[ii][j + 5];
x6 = A[ii][j + 6]; x7 = A[ii][j + 7];
B[j][ii] = x0; B[j + 1][ii] = x1;
B[j + 2][ii] = x2; B[j + 3][ii] = x3;
B[j][ii + 4] = x4; B[j + 1][ii + 4] = x5;
B[j + 2][ii + 4] = x6; B[j + 3][ii + 4] = x7;
}
for (ii = j; ii < j + 4; ii++)
{
x0 = A[i + 4][ii]; x1 = A[i + 5][ii];
x2 = A[i + 6][ii]; x3 = A[i + 7][ii];
x4 = B[ii][i + 4]; x5 = B[ii][i + 5];
x6 = B[ii][i + 6]; x7 = B[ii][i + 7];
B[ii][i + 4] = x0; B[ii][i + 5] = x1;
B[ii][i + 6] = x2; B[ii][i + 7] = x3;
B[ii + 4][i] = x4; B[ii + 4][i + 1] = x5;
B[ii + 4][i + 2] = x6; B[ii + 4][i + 3] = x7;
}
for (ii = i + 4; ii < i + 8; ii += 2)
{
x0 = A[ii][j + 4]; x1 = A[ii][j + 5];
x2 = A[ii][j + 6]; x3 = A[ii][j + 7];
x4 = A[ii + 1][j + 4]; x5 = A[ii + 1][j + 5];
x6 = A[ii + 1][j + 6]; x7 = A[ii + 1][j + 7];
B[j + 4][ii] = x0; B[j + 5][ii] = x1;
B[j + 6][ii] = x2; B[j + 7][ii] = x3;
B[j + 4][ii + 1] = x4; B[j + 5][ii + 1] = x5;
B[j + 6][ii + 1] = x6; B[j + 7][ii + 1] = x7;
}
}
for (j = 0; j < 60; j += 6)
for (ii = 64; ii < 67; ii++) //A[64][0]~A[67][59]部分进行3x6分块
{
x0 = A[ii][j]; x1 = A[ii][j + 1];
x2 = A[ii][j + 2]; x3 = A[ii][j + 3];
x4 = A[ii][j + 4]; x5 = A[ii][j + 5]; //一次性读取一行
B[j][ii] = x0; B[j + 1][ii] = x1;
B[j + 2][ii] = x2; B[j + 3][ii] = x3;
B[j + 4][ii] = x4; B[j + 5][ii] = x5;
}
for (i = 0; i < 64; i ++) //A[0][56]~A[63][59]部分
{
x0 = A[i][56]; x1 = A[i][57];
x2 = A[i][58]; x3 = A[i][59]; //一次性读取一行
x4 = A[i][60]; B[56][i] = x0;
B[57][i] = x1; B[58][i] = x2;
B[59][i] = x3; B[60][i] = x4;
}
B[60][64] = A[64][60]; //剩余直接转置
B[60][65] = A[65][60];
B[60][66] = A[66][60];
*/
}
}