【算法-数组1】二分查找 和 移除元素
今天,带来XXX的讲解。文中不足错漏之处望请斧正!
理论基础
二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
1. 思路
有序、不重复的数组,是个很让人嘴馋的条件,它天然地有很大优势。
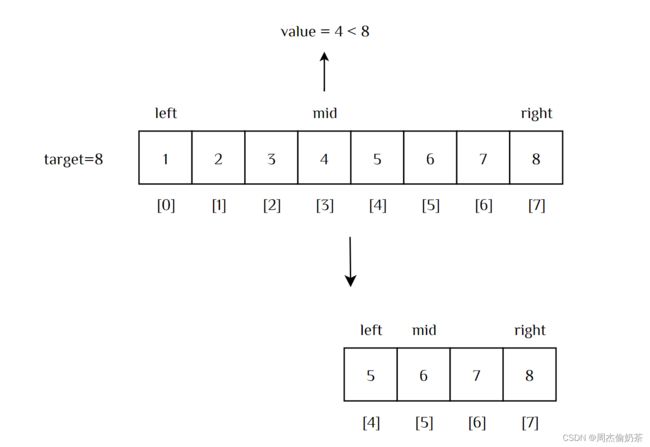
听过猜数游戏吗?猜1~100中的目标数,有最快的方法:每次把答案所处的范围缩小一半。
比如要猜78:
当前选数: 50
50小了,接下来的范围是:[50, 99]
当前选数: 75
75小了,接下来的范围是:[75, 99]
当前选数: 88
88大了,接下来的范围是:[75, 86]
当前选数: 81
81大了,接下来的范围是:[75, 79]
当前选数: 78
猜对了,78就是答案
每次,范围都能缩小一半,用当前选数来把整个范围一分为二。
这其实就叫二分查找算法:对于有序不重复的数组,每次取整个区间中间位置的值,判断这个值和目标谁大,中间值大,说明目标在左边,反之说明目标在右边。
2. 参考代码
2.0 循环不变量
很多朋友写二分法经常写乱,主要是因为对区间的定义没有想清楚,区间的定义就是不变量。要在二分查找的过程中,保持不变量,就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作,这就是循环不变量规则。
一般来说,left 和 right 有左闭右闭和左闭右开两种定义。
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0, right = nums.size() - 1;
while(left ? right) {
int mid = left + (right - left) / 2;
if(target < nums[mid]) right = ?;
if(nums[mid] < target) left = ?;
if(target == nums[mid]) return mid;
}
return -1;
}
};
细节1:while如何判断
while判断是<还是≤?
细节2:如何缩范围
确定了nums[mid]和target的关系,我们要怎么缩范围呢?这里难道不可以right = mid; left = mid;吗?
根据循环不变量确定细节
首先要根据题意来明确,我们搜索(查找)的区间是左闭右开还是左闭右闭。
- while判断:区间的定义
- 左闭右闭:
while(left ≤ right),因为left==right的时候,没有把整个数组搜索完,且[left,right]是合法区间 - 左闭右开:
while(left < right),因为left==right的时候,整个数组已经搜索完了,且[left,right)不是合法区间
- 左闭右闭:
- 缩范围:区间的定义 + 要缩范围时mid位置是否可被排除
- 左闭右闭+mid位置可被排除:
right = mid-1; left = mid+1 - 左闭右开+mid位置可被排除:
right = mid; left = mid+1 - 左闭右闭+mid位置不可被排除:
right = mid; left = mid - 左闭右开+mid位置不可被排除:
right = mid+1; left = mid
- 左闭右闭+mid位置可被排除:
2.1 左闭右闭版
所以回过头分析左闭右闭的写法:
- 当left==right,[left,right]是合法区间——while(left ≤ right)
- 左闭右闭+mid位置可被排除——right= mid - 1; left = mid + 1;
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0, right = nums.size() - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if(target < nums[mid]) right = mid - 1;
if(nums[mid] < target) left = mid + 1;
if(target == nums[mid]) return mid;
}
return -1;
}
};
2.2 左闭右开版
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0, right = nums.size();
while(left < right) {
int mid = left + (right - left) / 2;
if(target < nums[mid]) right = mid;
if(nums[mid] < target) left = mid + 1;
if(target == nums[mid]) return mid;
}
return -1;
}
};
- 当left==right,[left,right)是非法区间,如[1, 1)是非法的,不可能既包含1又不包含1——while(left < right)
- 左闭右开+mid位置可被排除:right = mid; left = mid+1
相关题目推荐
- 35.搜索插入位置(opens new window)
- 34.在排序数组中查找元素的第一个和最后一个位置(opens new window)
- 69.x 的平方根
- 367.有效的完全平方数
移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
1. 思路
1.1 暴力
两层循环,找到val就执行覆盖操作。
1.2 替换法
如果不关心顺序,可以用替换法,若当前位置等于val,把最后一个位置赋给当前位置,删除最后一个位置(尾删是O(1))。
1.3 双指针法
快指针遍历数组,找不需要移除的元素赋给慢指针。慢指针维护的是不需要移除的元素。
*图片来自代码随想录
2. 参考代码
2.1 暴力
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
size_t i = 0;
while(i < nums.size()) {
if(nums[i] == val) {
int cur = i, next = i + 1;
while(next < nums.size()) nums[cur++] = nums[next++]; //最后一个不用管了
nums.pop_back();
}
if(nums[i] != val) ++i; //覆盖后如果不判断就直接++i,可能跳过要移除的元素
}
return nums.size();
}
};
O(N^2)的时间复杂度,比较弱。
2.2 替换
class Solution2 {
public:
int removeElement(vector<int>& nums, int val) {
//不考虑元素顺序:替换法删除
size_t i = 0;
while(i < nums.size()) {
if(nums[i] == val) {
while(!nums.empty() && nums.back() == val) nums.pop_back();
if(i < nums.size()) {
nums[i] = nums.back();
nums.pop_back();
}
}
++i;
}
return nums.size();
}
};
O(N)的时间复杂度。
2.3 双指针
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int slow = 0;
for(size_t fast = 0; fast < nums.size(); ++fast) {
if(nums[fast] != val) nums[slow++] = nums[fast];
}
return slow;
}
};
O(N)的时间复杂度。
今天的分享就到这里了,感谢您能看到这里。
这里是培根的blog,期待与你共同进步!