二进制位运算的多种题目简单运用-自我回顾

---

题目1： 801. 二进制中1的个数

 本题有多种解法，在此运用lowbit运算

解题思路：

运用lowbit运算计数

lowbit运算：可以得到一个二进制数中最低位的1所对应的值

lowbit函数实现的两种方法：

1.   x & (~x+1)  

2.   x & -x

图例

 

-x 等价于 ~x+1，原因：根据计算机补码的性质，补码为原码取反后再+1

lowbit运算执行完之后只会得到最后一个1的位置，除了这个位置之外的所有位
置都会置为0

在该题目中的具体运用如下：

#include
using namespace std;
int lowbit(int x)
{
    return x & -x;//返回最后一位1
}
int main()
{
    int n;cin>>n;
    while(n--)
    {
        int x;
        cin>>x;
        int res=0;
        while(x)
        {
             x -= lowbit(x);
             res++;
        }
        cout<

 代码解析：

 x -= lowbit(x):

由上面的lowbit运算用途我们可以得知，lowbit(x)会返回x中最低位的1代表的值，

x -= lowbit,即减掉最低位的1，同时运用计数器res进行计数

lowbit运算的类似简单运用

 

题目2：2的幂 - LeetCode

给定整数n，判断是否为2的幂次方:

由上文我们得知lowbit运算可以得到最低位1的数

class Solution {
public:
    bool isPowerOfTwo(int n) 
    {
        //lowbit运算
        return (n>0) && (n & (~n+1)) == n ;
        // return (n>0) && (n & -n) == n;
    }
};

对于

n & (~n+1) == n 代码的解析:

当一个数为2的幂次方的时候,当它表示为二进制数时，通过lowbit运算得到的最低位的1同时也是唯一的一个1，因为2,4,8,16,32,64······表示为二进制数都只有一个位上为1

所以: 通过n & (~n+1) == n  表达式的判断可以得出该数是否为2的幂次方

leetcode运行结果

 

同类题目运用

题目3： 4的幂

思路：只需把4的幂转换成2的幂进行判断

class Solution {
public:
    bool isPowerOfFour(int n) 
    {
        if(n <= 0) return false;
        int x=sqrt(n);
        return x*x==n && (x& -x) == x;
    }
};

 代码运行结果:

 以上即为lowbit运算的简单运用，不涉及树状数组

--------------------------------------------------------------------------------------------------------------------------------

2道位运算的经典题目:

题目1: 剑指offer65.不用加减乘除做加法

解题思路： 运用二进制位运算 

class Solution {
public:
    int add(int a, int b) 
    {
        //模拟加法
        while(b != 0)
        {
            int tmp=(unsigned int)(a&b)<<1;//求得进位数
            a=a^b;//无进位求和
            b=tmp;//进位数
        }
        return a;
    }
};

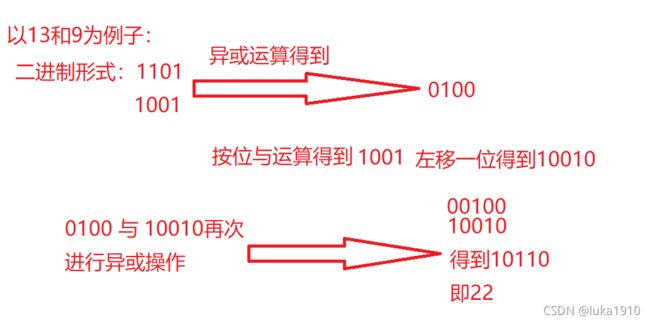
解析:

^ 亦或 ----相当于 无进位的求和

 

& 与 ----相当于求每位的进位数

代码解析:

 int tmp=(unsigned int)(a&b)<<1;//求得进位数

由于在LC C++中不支持负值左移，所以强转为无符号数

题目2：剑指Offer 56 - 数组中数字出现的次数  

 解题思路：

先通过异或去除重复数字，再通过位运算分离2个不重复的数字

代码：

int* singleNumbers(int* nums, int numsSize, int* returnSize)
{
    int tmp=0;
    for(int i=0;i

以测试用例2 2 4 1 6 4 进行模拟 

第一个for循环执行后为

tmp = 2^2^4^1^6^4 即 tmp = 1^6

通过whle循环(m<32)来寻找二进制位中的1

（此处同时也可运用lowbit运算,因为只需要找一个1即可，最低位的1也不影响结果）

即 int m = tmp & (-tmp);

再次运用异或进行分组

为什么能分组，原因：

当进行完异或运算之后，tmp= 1^6，此时的tmp中二进制的1必为1和6不相等的位数,即1在此位为0而6在此位为1（异或性质）

再通过while循环找到tmp二进制位中的1

此时再判断（数组中的每一个元素和第m位的1按位与操作是否为1）即可实现a1和a2两个不重复数字的分离,在该测试用例中a1组只得到1，a2组得到2^2^4^6^4,即4

当循环执行完即找到两个不重复的数字a1和a2

代码运行结果 (C) 

---------------------------------------------------------------------------------------------------------------------------------

以上即为对几道经典位运算题目的解析回顾，如有疑惑或指正请发表在评论区

---------------------------------------------------------------------------------------------------------------------------------