树----数据结构
树的概念
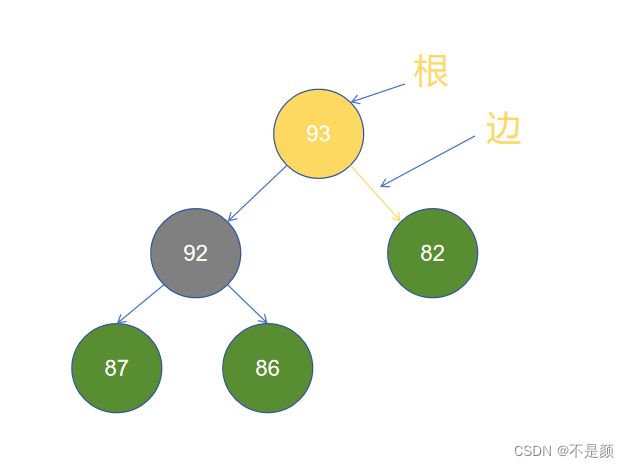
树是一种非线性的数据结构,它是由 n (n>=1) 个有限结点组成一个具有层次关系的集合,它看起来就像一颗倒挂的树,根朝上,叶朝下。由 0 个节点构成的树,叫做空树。
树的特点:每个结点有 0 个或多个子结点。没有父节点的结点称为根结点。每个非根结点有且只有一个父结点。除了根结点以外,每个子结点可以分成多个不相交的子树。(节和结都一样)
| 专业术语 | 中文 | 描述 |
|---|---|---|
| Root | 根节点 | 一棵树的顶点 |
| Child | 孩子节点 | 一个节点含有的子树的根节点称为该节点的孩子节点 |
| Leaf | 叶子节点 | 没有孩子的节点 |
| Degree | 度 | 一个节点包含的子树的数量 |
| Edge | 边 | 一个节点与另一个节点的连接 |
| Depth | (节点)深度 | 根节点到这个节点最长路径的经过的边的数量 |
| Height | (节点)高度 | 从当前节点到叶子节点形成的最长路径中边的数量 |
| Level | (节点)层级 | 节点到根节点最长路径的边的总和 |
| Path | 路径 | 一个节点和另一个节点之间经过的边和 Node(节点)的序列 |
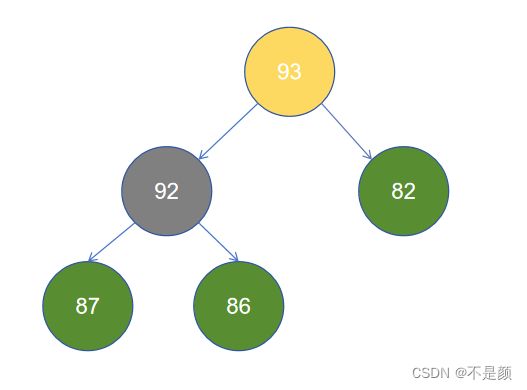
其中 93 是根节点,92 和 82 是 93 的孩子节点,87、82、86 是叶子节点,93 与 82 的连接线为边,不知道你有没有听过梅开二度?当然和这个关系不大,93 的度数为 2 ,因为它有两个子节点(分了两个岔),那当然 82 的度数就为 0 。
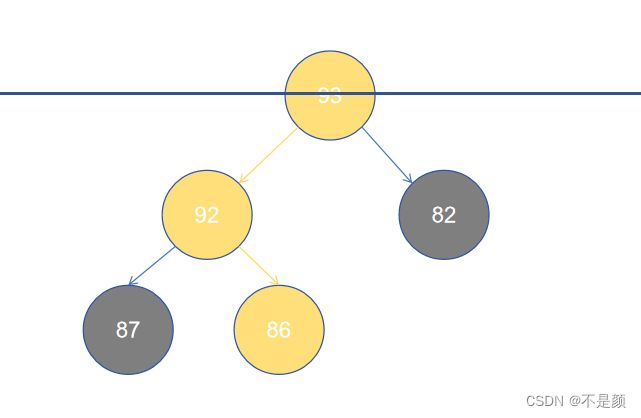
黄颜色的就是一条路径, 93 到 92 到 86。另外 86 的深度为2(到根节点的路径的边的数量),93 的深度为0,可以将根节点所在的水平当做水平面,那么你和根节点的距离就是深度了。
既然有深度,那就有高度,93 的高度为 2,可不是 1 ,因为高度取得是到叶子节点的最长路径的边数之和。
也就是节点的深度,93 的层级为 0,86 的层级为 2。
以上的概念个人认为多看看就好了,重点在下面(因为有些定义不是统一的,可能会和别人的文章有区别)。
二叉树的概念
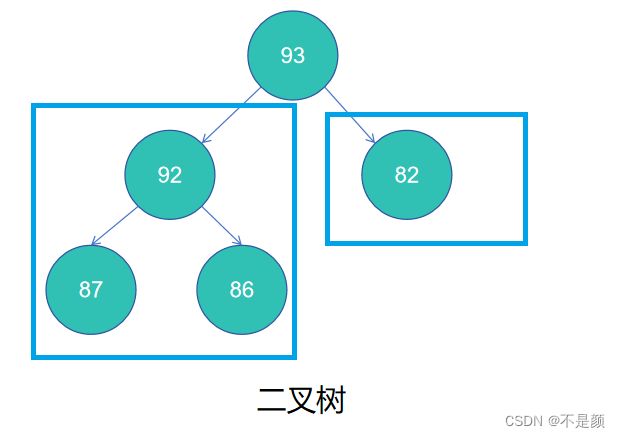
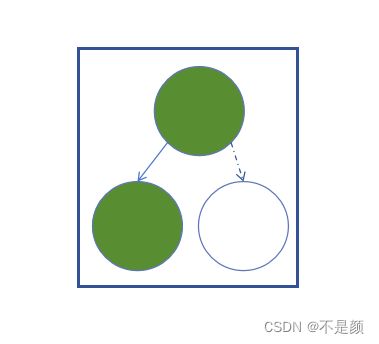
如同线性表与栈、队列的关系,二叉树就是操作受限的树,那二叉树就是一个 一个节点最多只有两个分支的树(一个父节点最多有两个子节点),不一定一个节点一定是有两个子节点,左边的分支叫做左子树,右边的分支叫做右子树。
如图框框框住的就是子树。:
二叉树的一些性质
1、在非空二叉树中,第 i-1 层的节点总数不超过
,i >= 1
2、深度为 h-1 的二叉树最多有
- 1 个节点(h>=1),最少有 h 个节点
3、对于任意一颗二叉树,如果其叶子节点的数为 N0 ,而度数为 2 的节点的总数为 N2 ,则N0 = N2 + 1
(定义可能和书有所不同,但是意思是一样的)
对于第一点:因为第 0 层的最大节点数为 1 ,第 1 层的最大节点数为 2 ,下一层是上一层的 2 倍,以此类推。对于第二点:也能从第一点中得到深度为 h-1 的最多的节点数,最少的节点就是所有的父节点都只有一个子节点的情况。(注意是整个二叉树的节点总数)。对于第三点:二叉树最开始时只有一个根节点,叶子节点数为 1,只要根节点有两个子节点(分了两个岔路,变为了度数为 2 的节点),那叶子节点数就加 1 ,因为到最后,两个子节点的最下面一定有两个叶子节点,以此类推。
常见二叉树的分类
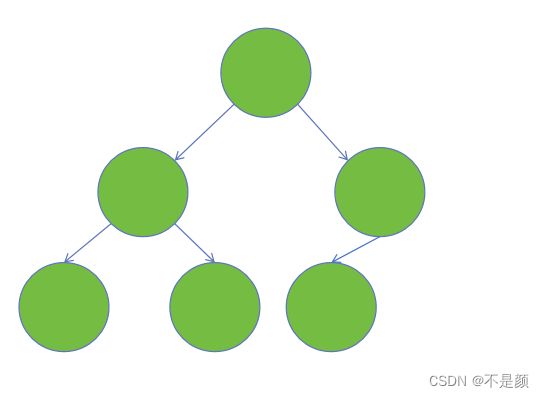
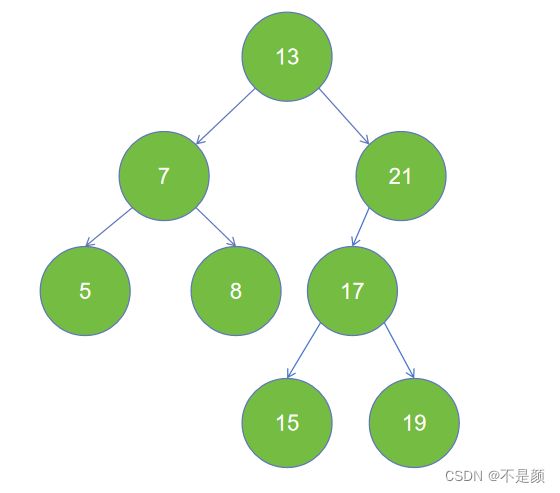
(1)完全二叉树-设二叉树的深度为 h,除了第 h 层外,其他层 (0~h-1) 的节点数都达到了最大个数,第 h 层有叶子节点,并且叶子节点是从左到右依次排列的,这就是完全二叉树(堆就是完全二叉树)。
如图,这就是一个完全二叉树。
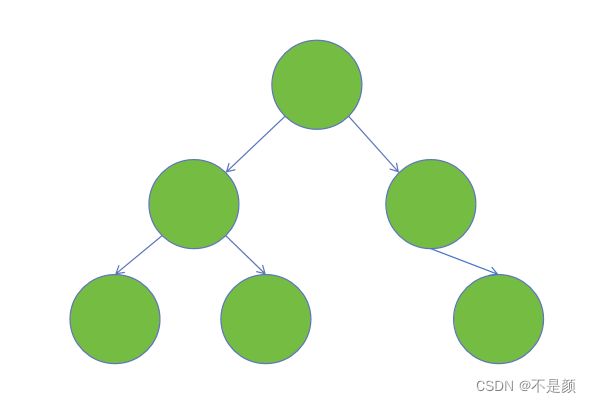
那叶子节点依次排列是什么意思呢?如下图这就不是一个完全二叉树,因为叶子节点不是依次排列的,第二个和第三个叶子节点中有个空位。
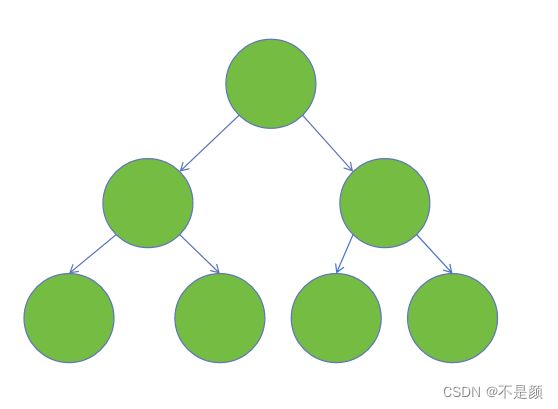
(2)满二叉树-除了叶子节点外每一个节点都有左右子节点,且叶子节点处于最低层的二叉树。(也就是每层都是满的,每一层节点数达到最大),如图:
(3)平衡二叉树-又称 AVL 树,它是一颗空树(一个节点也没有)或者左右两个子树的高度差的绝对值不超过 1 ,并且左右两个子树都是平衡二叉树。
这里得注意:树的高度和节点的高度不同,因为层级是从 0 开始的,所以树的高度为层数 + 1 。
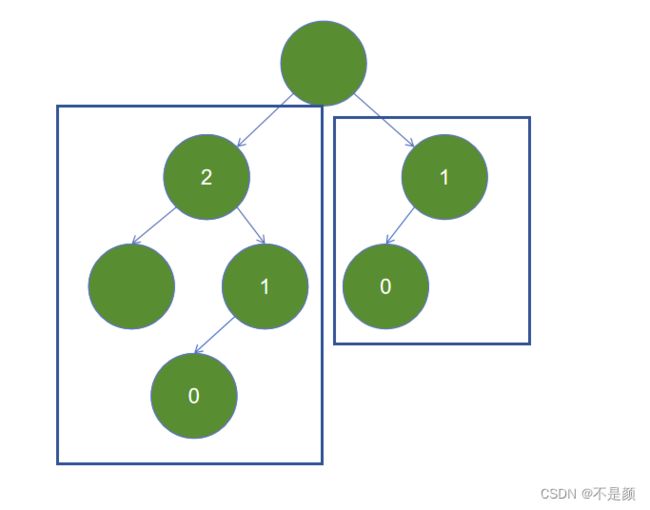
看,左子树的高度为 3 ,右子树的高度为 2 ,满足条件,别忘了子树也是平衡二叉树,和刚刚的分析一致,例如把右子树拿出来分析,如下图。
当节点的数量为 1 时,为空子树(没有孩子),高度为 1 ,故左子树的高度为 1 ,而右边啥也没有,那高度就是 0 。
(4)二叉搜索树-又称二叉查找树、二叉排序树,它是一颗空树或是满足下列性质的树:
1.若左子树不为空,则左子树上所有节点的值都小于等于它的根节点的值。
2.若右子树不为空,则右子树上所有节点的值都大于等于它的根节点的值。
3.左右子树也为二叉排序树。
二叉排序树例子:
那二叉排序树的作用是什么呢?可以用来快速地查找数据,比如有一亿个数据,要查找某个数据,理想状态只需要 27次操作就能找到,不需要遍历一亿次,是二分查找的一种特殊形式。
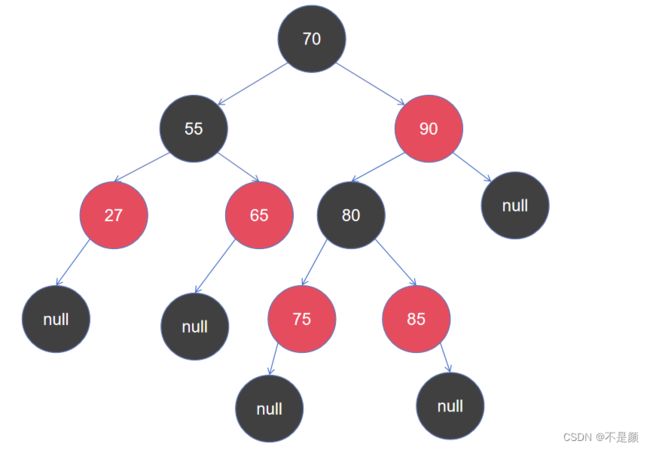
(5)红黑树-是每个节点都带有颜色属性(颜色为红色或者黑色)的自平衡二叉查找树,满足下列性质:
1.首先要满足二叉查找树的性质
2.节点是红色或黑色
3.根节点是黑色
4.所有的叶子节点是黑色
5.每个红色节点的子节点一定是黑色的,黑色节点的子节点无要求(从每个叶子到根的所有路径上不能有两个连续的红色节点)
6.从任一节点到其叶子节点的所有简单路径都包含相同数目的黑色节点
二叉搜索树的算法实现
引入:有一个一维数组,需要在这个数组中找到某个数字,可以遍历数组,可是这种方式效率太低。让数组有序,使用折半法(二分查找)就快得多了,可是如果需要删除或者添加数据,为了能够继续使用二分查找,就需要将数组排序,这需要移动大量的数据,显然可以使用链表存储数据,方便数据的查找和删除,可是链表却不能快速查找位置,通过比较一次排除一部分元素。
这时候二叉搜索树的应用就出现了,根据二叉搜索树的性质可以得出,它是这个场景的最佳选择(查找插入频率高)。
二叉树一般采用链式存储方式,每个节点包含两个指针域,分别指向左右孩子节点,还包含了一个数据域,存储节点的信息。如下图:
typedef int TreeDateElem;
typedef struct _BNode //二叉树
{
TreeDateElem date; //元素类型
struct _BNode* l; //指向左右孩子节点
struct _BNode* r;
}BNode, BTree;二叉搜索树的插入
将插入的结点与根节点进行比较,如果小于等于就和左子节点进行比较,大于就和右子节点进行比较(是由二叉搜索树的性质得出的)。重复以上步骤,直到找到一个空位置,这样就可以插入了。
bool insertBtree(BNode** root, BNode* node)
{
BNode *temp = NULL, *parent = NULL;
if (!node)
{
return false;
}
else //初始化插入节点的左右子树
{
node->l = NULL;
node->r = NULL;
}
if (!*root) //根节点为空,也就是空树
{
*root = node;
return true;
}
else
{
temp = *root;
}
while (temp != NULL)
{
parent = temp; //parent 保存父节点
if (node->date <= temp->date)
{
temp = parent->l;
}
else
{
temp = parent->r;
}
}
if (node->date < parent->date) //此时temp==NULL(找到空位置),可以进行插入
{
parent->l = node;
}
else
{
parent->r = node;
}
return true;
}二叉搜索树的删除
二叉树中节点的状态有 5 种,分别是为空、无左右子节点(叶子节点)、无左子节点、无右子节点、有左右子树(有左右子节点),对应删除操作也要分情况。
首先要比较要删除节点的值,找到节点位置。插入时已经实现过了
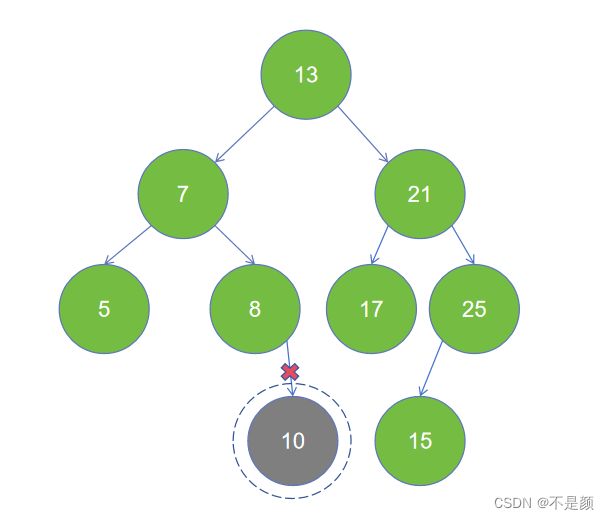
情况一:要删除的节点不存在左右子节点,即为叶子节点,直接删除它。
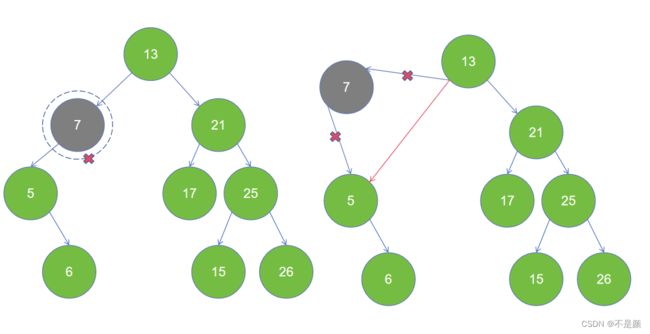
情况二:要删除的节点存在左子节点,不存在右子节点,直接将它的父节点的左孩子指针指向它的左子节点(也就是用左子节点代替它)。
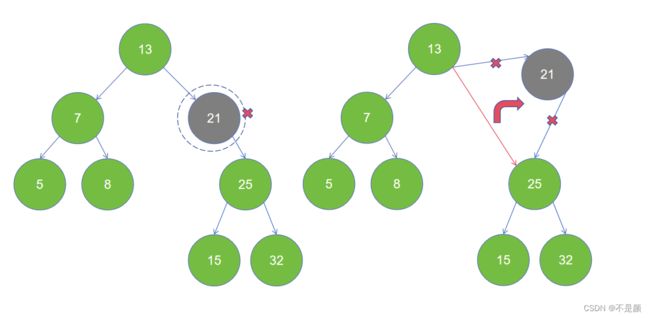
情况三:要删除的节点存在右子节点,不存在左字节点,用右子节点代替删除节点(和情况二类似)。
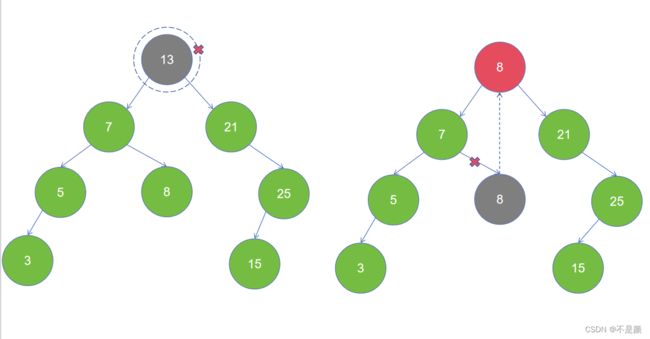
情况四:要删除的节点存在左右子节点,则取左子树上的最大节点,或者取右子树上的最小节点来代替要删除的节点。
图为第一种情况:
看替换后还是一颗二叉搜索树,你也可以用右子树的最小节点替换。
//二叉树的删除(采用递归的方式)
BTree* deleteBtree(BTree *root, TreeDateElem date)
{
if (root == NULL) return NULL; // 没有找到节点
if (date < root->date)
{
root->l = deleteBtree(root->l, date);
return root;
}
else if (date > root->date)
{
root->r = deleteBtree(root->r, date);
return root;
}
//说明找到了,因为没有继续递归
//情况一:
if (root->l == NULL && root->r == NULL) return NULL; //将这个节点的父节点置为空
//情况二:
if (root->l == NULL && root->r != NULL) return root->r; //左子节点取代
//情况三:
if (root->l != NULL && root->r == NULL) return root->l; //右子节点取代
//情况四
if (root->l != NULL && root->r != NULL) //将左子树最大的节点的值赋给这个节点,再将左子树最大的节点删除
{
int val = findMax(root->l);
root->date = val;
root->l = deleteBtree(root->l, val);
return root;
}
//注意删除函数中并没有释放内存,可以在参数中加一个指针变量,把要删除的节点的地址返回,在主函数中释放内存
return NULL; //运行不到这步,只是为了消除 不是所有的控件路径都返回值 的警告
}其中查找左子树(树)最大的节点的函数是下面这个
int findMax(BTree* root)
{
assert(root != NULL);
//循环实现
/*while (root->r != NULL)
{
root = root->r;
}
return root->date;*/
//递归实现
if (root->r == NULL)
{
return root->date;
}
return findMax(root->r);
}二叉树查找节点
BNode* queryNode(BTree* root, TreeDateElem e)
{
//(递归实现)
if (root == NULL || root->date==e)
{
return root;
}
else if(root->date < e )
{
return queryNode(root->r, e); //查询右子树
}
else if(root->date > e )
{
return queryNode(root->l,e); //查询左子树
}
return NULL; //运行不到这步,只是为了消除 不是所有的控件路径都返回值 的警告
循环实现
//while (root != NULL && root->date != e)
//{
// if (root->date < e)
// {
// root = root->r;
// }
// else if (root->date > e)
// {
// root = root->l;
// }
//}
//return root;
}二叉树的遍历
二叉树的遍历是从根节点开始,依次访问各个节点,且每个节点仅访问一次,有四种遍历方式:
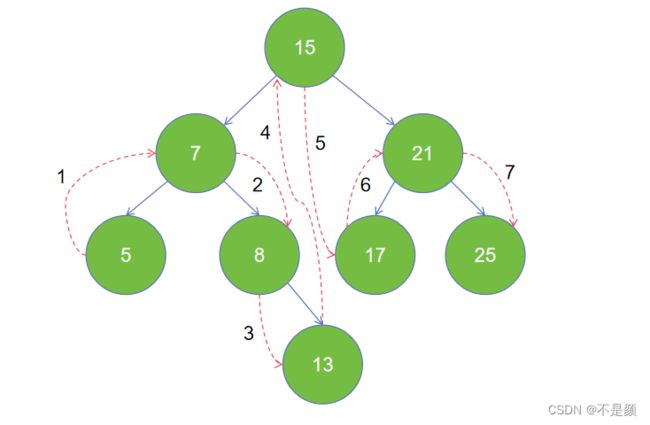
前序遍历-先访问根节点,然后前序遍历左子树,再前序遍历右子树。
上图的遍历结果是:13 7 5 8 15 21 17 26
递归实现:
void visitTree2(BTree * root)
{
if (root == NULL)
{
return;
}
printf("-%d-", root->date);
visitTree2(root->l);
visitTree2(root->r);
}循环实现(非递归)申请一个栈,首先将头结点压入栈中。然后出栈,打印出栈元素的值,如果右孩子不为空,就将右孩子压入栈中,如果左孩子不为空,就将左孩子压入栈中。重复此操作直至栈为空。
void visitTree3(BTree* root)
{
BNode cur;
if (root == NULL)
{
return;
}
Stack stack;
initStack(stack);
pushStack(stack, *root);
while (!IsEmpty(stack))
{
popStack(stack, cur);
printf("-%d-", cur.date);
if (cur.r != NULL)
{
pushStack(stack, *(cur.r));
}
if (cur.l != NULL)
{
pushStack(stack, *(cur.l));
}
}
destoryStack(stack);
}中序遍历-先访问根节点的左子树,再访问根节点,最后访问右子树。(这也是一个递归的过程,对于它的左子树也是先访问左子树,再访问根节点,最后访问右子树)
上图的遍历结果是:5 7 8 13 15 17 21 25
递归实现
void visitTree(BTree* root)
{
if (root == NULL)
{
return;
}
visitTree(root->l); //是不是so easy!重在理解
printf("-%d-", root->date);
//visitTree(root->l);
visitTree(root->r);
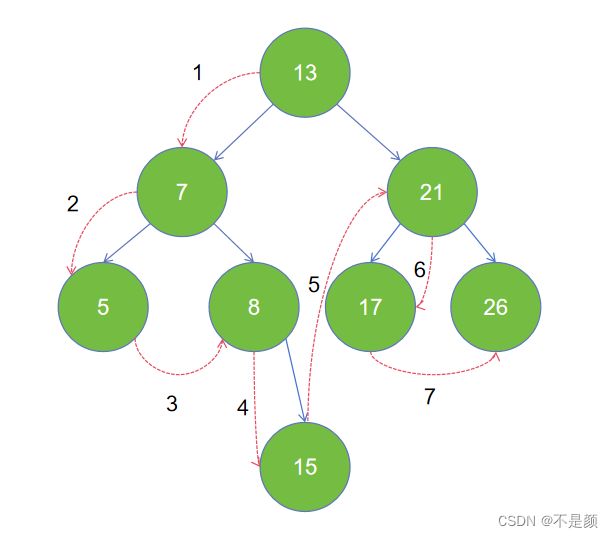
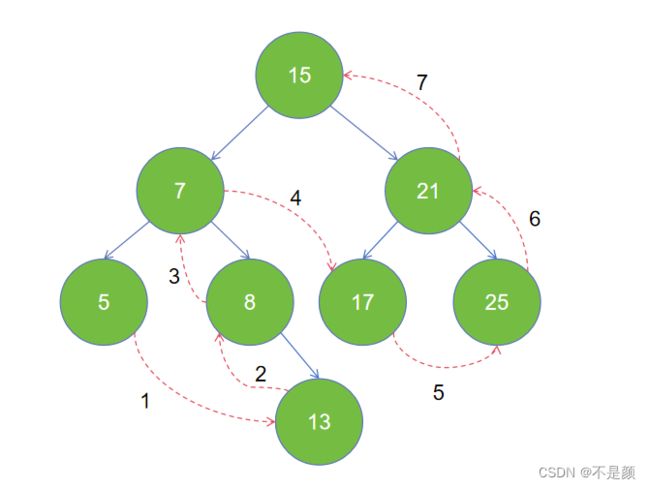
}后序遍历-从左到右先叶子再节点的方式访问左右子树,最后是根节点。(也是一个递归的过程,先访问左子树,再访问右子树,最后访问根节点。访问左子树时,继续这个操作……)
上图的遍历结果是:5 13 8 7 17 25 21 15
后续遍历的代码就不写了。
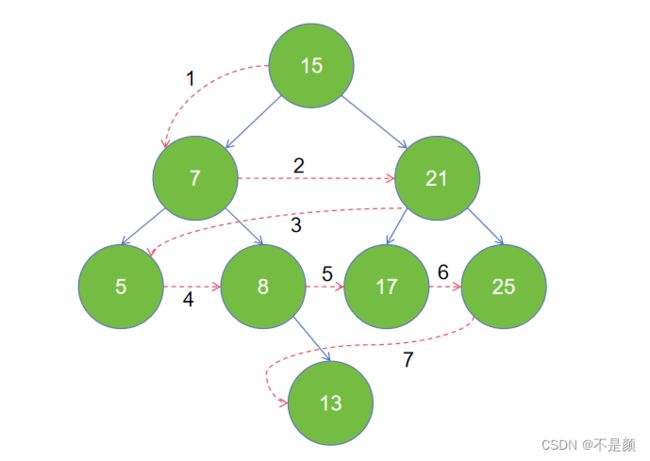
层序遍历-从根节点从上往下逐层遍历( 0 层、1 层、2层……),对于同一层的节点,按照从左到右的顺序访问。
上图的遍历结果是:15 7 21 5 8 17 25 13
层序遍历的代码也不贴了,可以自己独立完成,可以队列实现。
最后是主函数的测试代码
其中栈的实现我也没贴出来。
int main(void)
{
int arr[] = { 19,7,25,5,11,15,21,61 };
BTree *tree = NULL;
BNode *node = NULL;
for (int i = 0; i < sizeof(arr) / sizeof(int); i++)
{
node = new BNode;
node->date = arr[i];
if (insertBtree(&tree, node)) //传递的是一级指针的地址,所以用二级指针接收
{
cout << "节点" << arr[i] << "插入成功" << endl;
}
else
{
cout << "节点" << arr[i] << "插入失败" << endl;
}
}
cout << "前序遍历的结果:"<date);
}
else
{
printf("表中无此节点\n");
}
return 0;
}