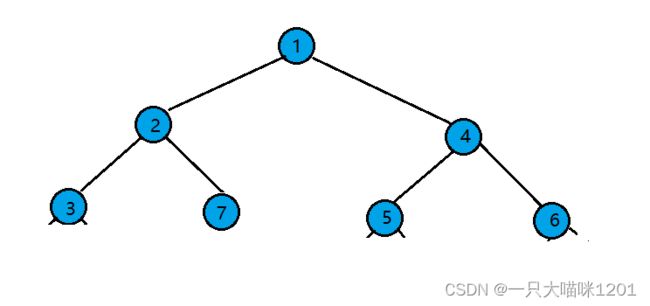
【数据结构与算法】二叉树OJ练习题
作者：一只大喵咪1201
专栏：《数据结构与算法》
格言：你只管努力，剩下的交给时间！
习题
- 单值二叉树
- 检查两颗树是否相同
- 对称二叉树
- 二叉树的前序遍历
- 另一颗树的子树
- 判断二叉树是否是完全二叉树
- 选择题
现在初级二叉树已经学习完了，来做一些题巩固一下。
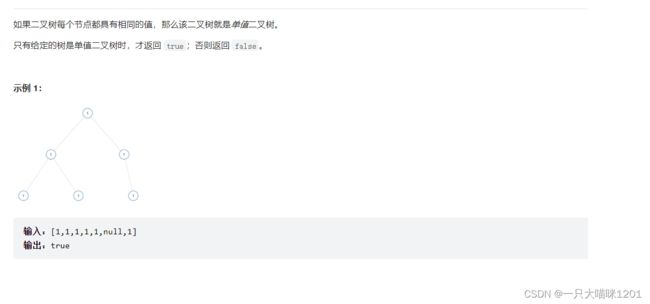
单值二叉树
习题链接
题目描述：
分析：
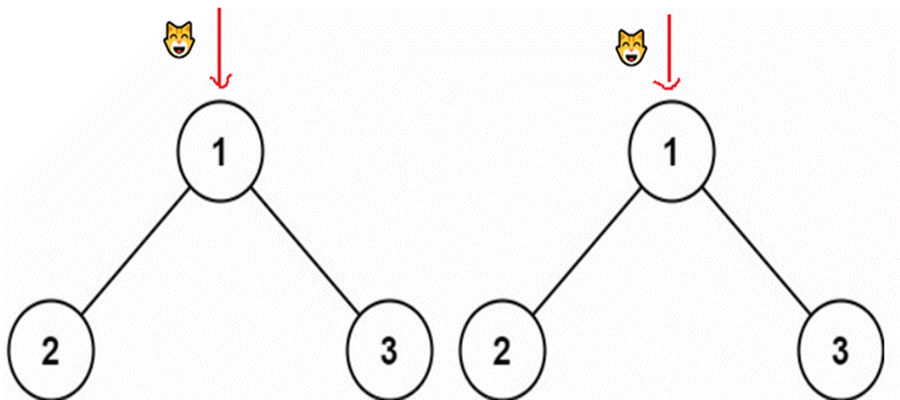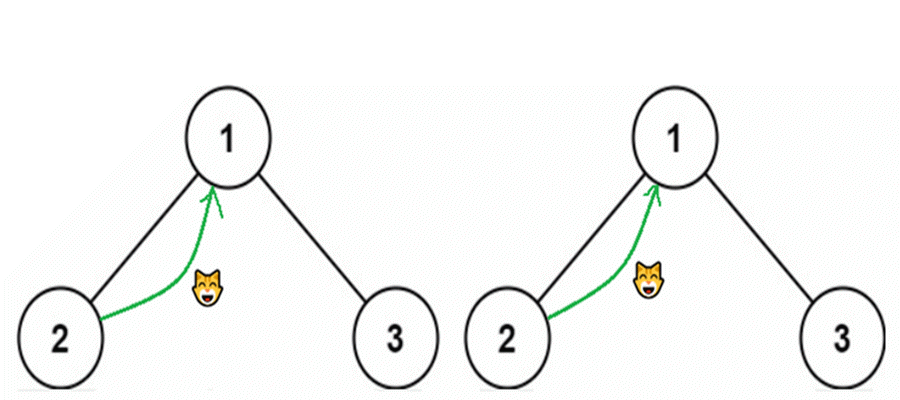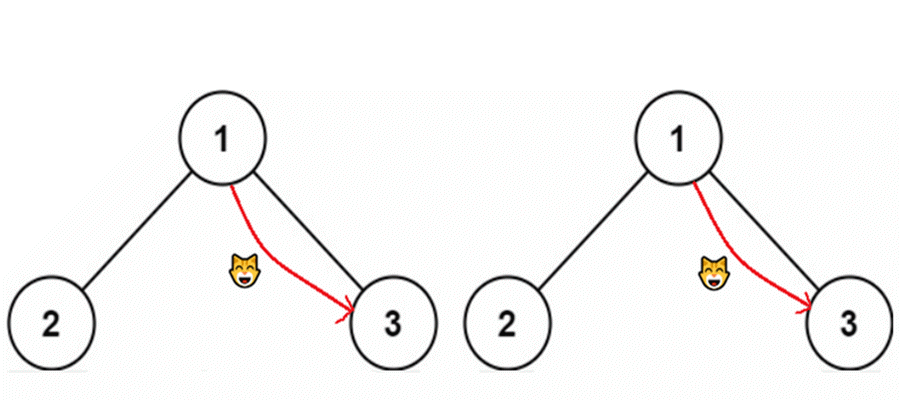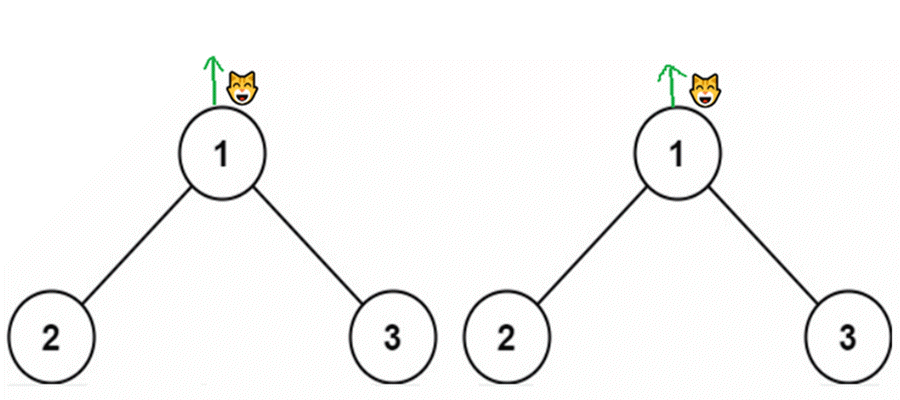
这是流程图，红线是递归过程，绿线是回退过程。
思路：分治思想
- 根节点和子树相比较，如果相等就继续递归，不相等就返回false
- 当根节点是NULL的时候返回true
代码实现：
bool isUnivalTree(struct TreeNode* root){
//返回条件
if(root==NULL)
return true;
//左右子树判断
if((root->left)&&(root->val != root->left->val))
return false;
if((root->right)&&(root->val != root->right->val))
return false;
//递归
return isUnivalTree(root->left)&&isUnivalTree(root->right);
}
接下来看下函数栈帧调用图
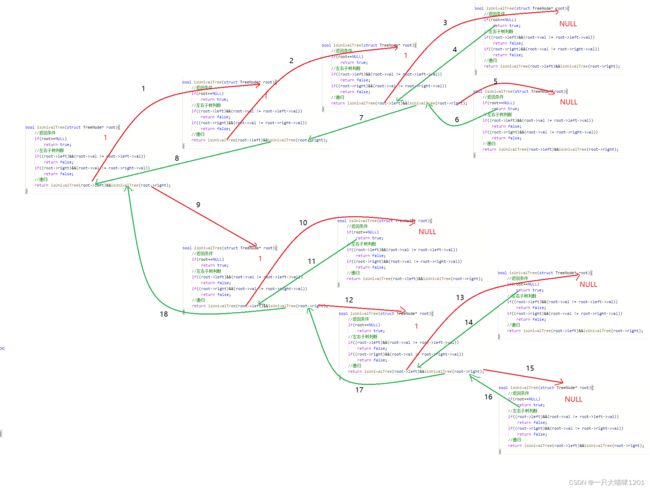
红色线是递归过程，绿色线是回退过程，黑色数字是它的执行顺序。
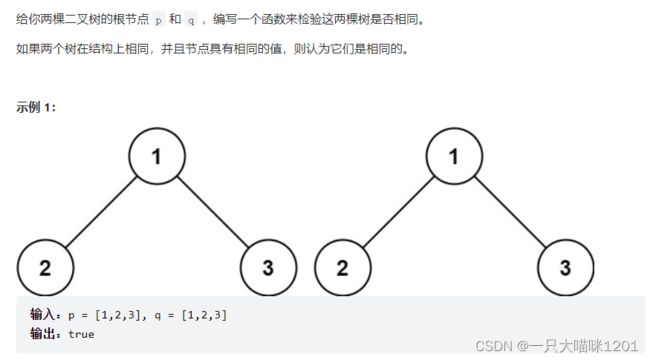
检查两颗树是否相同
习题链接
题目描述：
分析：
这是流程图，红线是递归过程，绿线是回退过程。
思路：分治思想
- 俩颗树根节点相比，左子树相比，右子树相比
- 节点同时为空，相等，返回真
- 只有一个节点为空，不相等，返回假
- 俩个根节点不相等，返回假
- 俩颗树根节点相比，左子树相比，右子树相比，左右子树必须都相同。
代码实现：
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
//同时为空，相等
if(p==NULL && q==NULL)
return true;
//只有一个为空，不相等
if(p==NULL||q==NULL)
return false;
//俩个节点值不相等
if(p->val!=q->val)
return false;
return isSameTree(p->left,q->left)
&&isSameTree(p->right,q->right);
}
函数栈帧调用图：
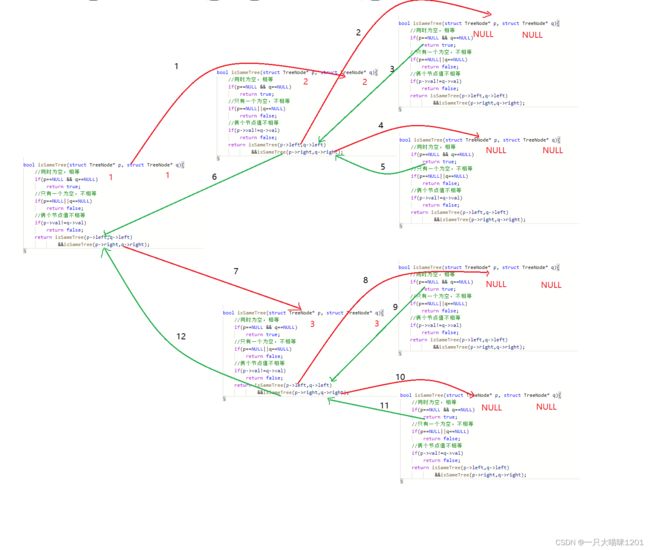
红色线是递归过程，绿色线是回退过程，黑色数字是它的执行顺序。
- 举的例子中是相等的，所以会一直走下去，如果有不相等的，就会提前返回false。
对称二叉树
习题链接
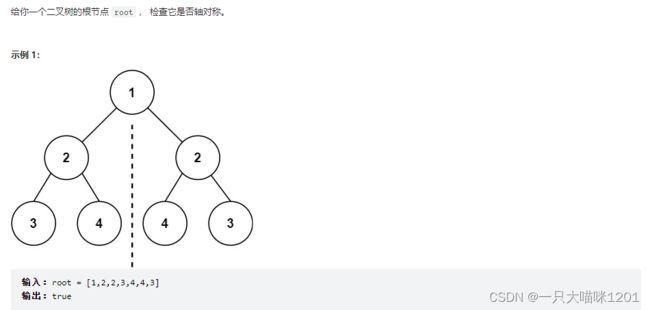
题目描述：
分析：
这个动图是访问顺序图，红线是递归，绿线是回退。
思路：分治思想
- 从根节点处将树分为俩颗
- 当节点同时为空返回真，一个为真返回假
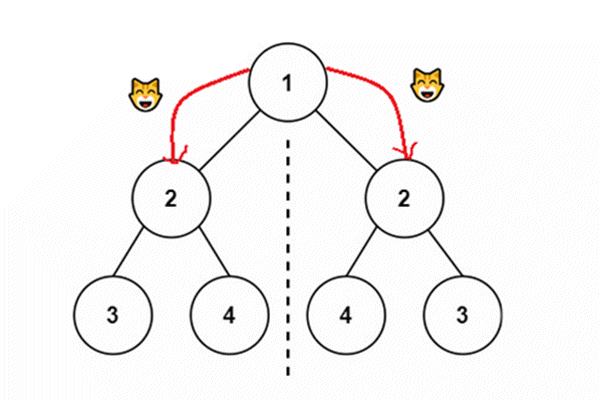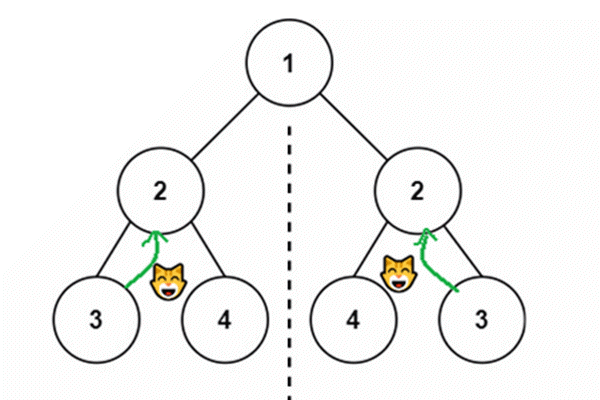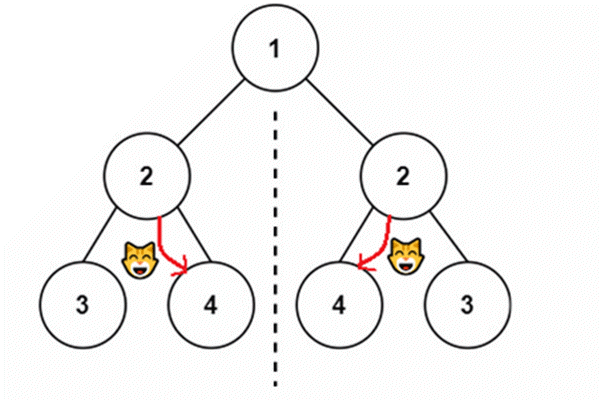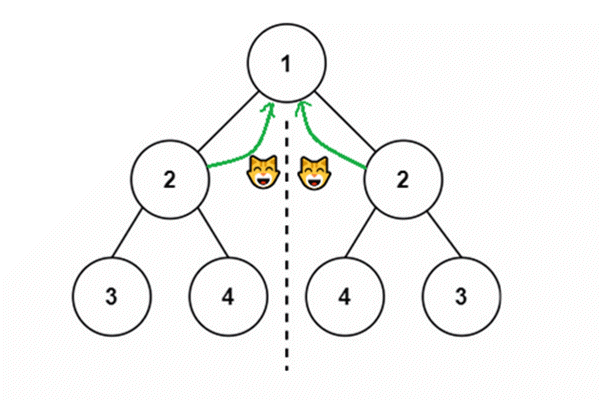
- 俩棵子树的节点作比较，左子树的左子节点与右子树的右子节点比较，左子树的右子节点和右子树的左子节点比较
- 递归下去
代码实现：
bool compare(struct TreeNode* left,struct TreeNode* right)
{
//左右子树节点同时为空
if(left==NULL&&right==NULL)
return true;
//只有一个为空
if(left==NULL||right==NULL)
return false;
//俩个节点不相等
if(left->val!=right->val)
return false;
//左子树左节点与右子树右节点，左子树右节点与右子树左节点
return compare(left->left,right->right) && compare(left->right,right->left);
}
bool isSymmetric(struct TreeNode* root){
//看传进来的是否为空树
if(root==NULL)
return true;
//分成俩个子树比较
return compare(root->left,root->right);
}
函数栈帧调用图：
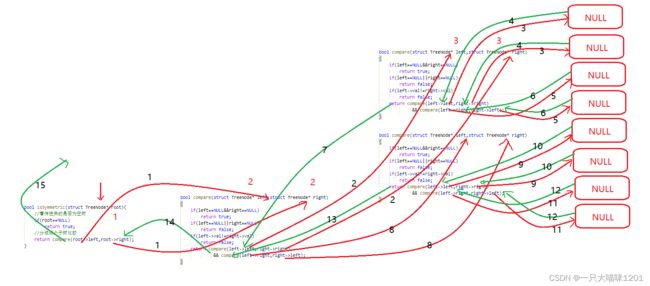
红色线是递归过程，绿色线是回退过程，黑色数字是它的执行顺序。这个栈帧调用画的非常混乱，只需要看执行顺序图就可以写出代码。
- 俩棵树同时在进行，所以同样的黑色数字表示在同时进行。
二叉树的前序遍历
习题链接
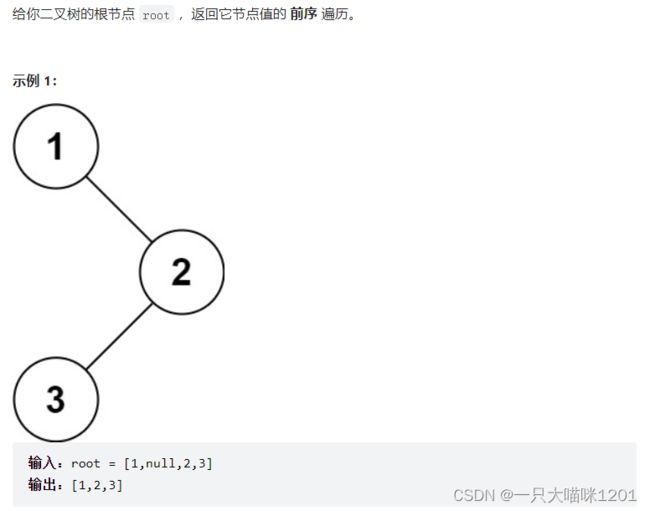
题目描述：
分析：
思路：
- 按照前序遍历的方式，将每个节点的值存放在动态开辟的数组中。
代码实现：
int TreeSize(struct TreeNode* root)
{
if(root==NULL)
return 0;
return 1+TreeSize(root->left)+TreeSize(root->right);
}
void PreOrder(struct TreeNode* root,int* data,int* pi)
{
if(root==NULL)
return;
data[*pi]=root->val;//存入
(*pi)++;//下标加1
PreOrder(root->left,data,pi);///左子树
PreOrder(root->right,data,pi);//右子树
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
int n = TreeSize(root);//求出节点个数
int* data=(int*)malloc(sizeof(int)*n);//开辟n个空间
int i = 0;
PreOrder(root,data,&i);//前序储存
*returnSize=n;//返回个数
return data;//返回数组
}
求节点个数，前序遍历在本喵的上篇文章中有过详细讲解，这里就不再阐述。
注意
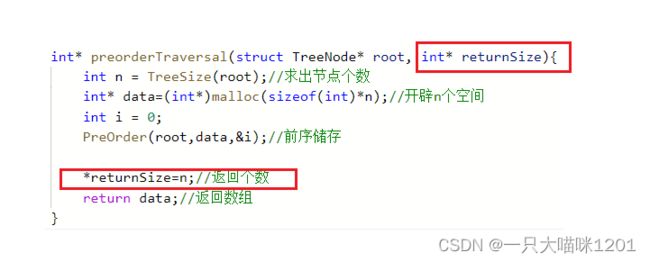
红色框中的变量不是给我们用的，而是要返回的。因为一个函数很难返回多个值，所以采用传址调用来间接带回另外一个值。
同样的还可以实现中序遍历，后序遍历，这里本喵就不写了，有兴趣的小伙伴自己去写一下哦。
另一颗树的子树
习题链接
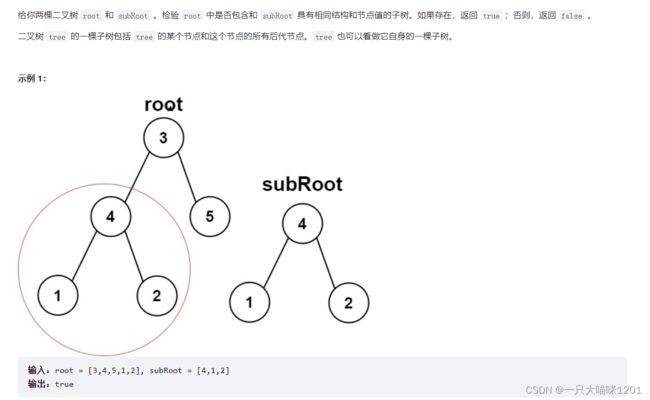
题目描述：
分析：
思路：前序遍历的思路
- 将树的每一个节点都和子树进行比较。
代码实现：
bool isSeamTree(struct TreeNode* p,struct TreeNode* q)
{
if(p==NULL&&q==NULL)
return true;
if(p==NULL||q==NULL)
return false;
if(p->val!=q->val)
return false;
return isSeamTree(p->left,q->left)&&isSeamTree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
//如果是空，肯定不存在子树
if(root==NULL)
return false;
//看是否是另外一颗子树
if(isSeamTree(root,subRoot))
return true;
//左右子树中有一个符合
return isSubtree(root->left,subRoot)
||isSubtree(root->right,subRoot);
}
其中，判断俩棵树是否相等的函数是我们前面题目中的代码，直接复制过来用即可。
来看函数栈帧递归调用图
红色的是递归过程，绿色的退回过程，黑色数字是执行顺序。
判断二叉树是否是完全二叉树
判断这样一个树是否是完全二叉树。
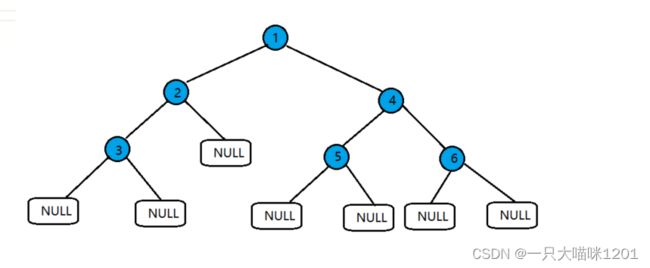
分析：
思路：层序遍历的思路
- 将二叉树的根节点入队列，再出队列，并且将它的左右子节点入队列
- 再出左节点，同时将左节点的左右节点入队列
- 再出右节点，同时将右节点的左右节点入队列
- 如此反复，类似于层序遍历，当队首元素是空的是时候，判断队列是否为空
- 如果是空队列，则是完全二叉树，否则就是非完全二叉树。
像动图中那样，一直在层序遍历，直到队首元素为NULL时停止遍历。
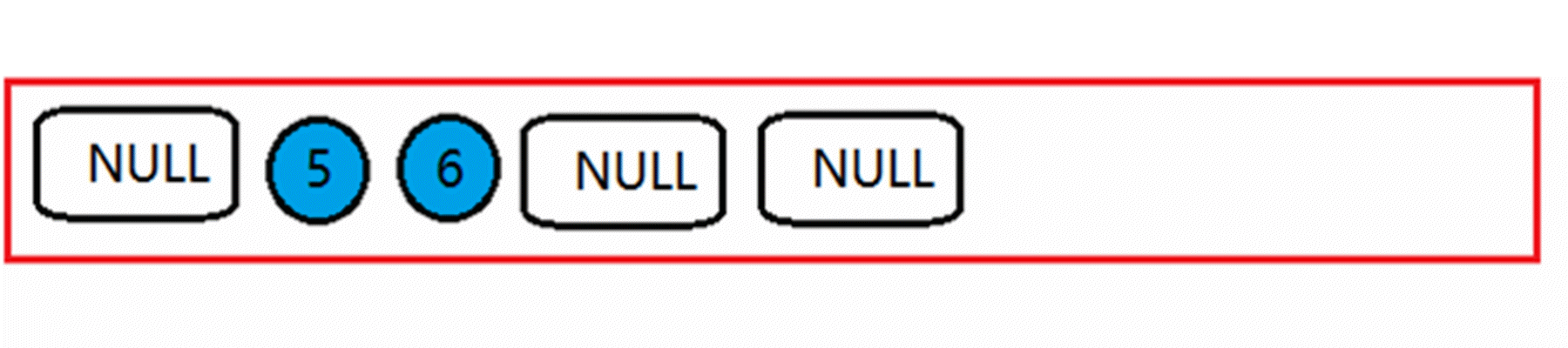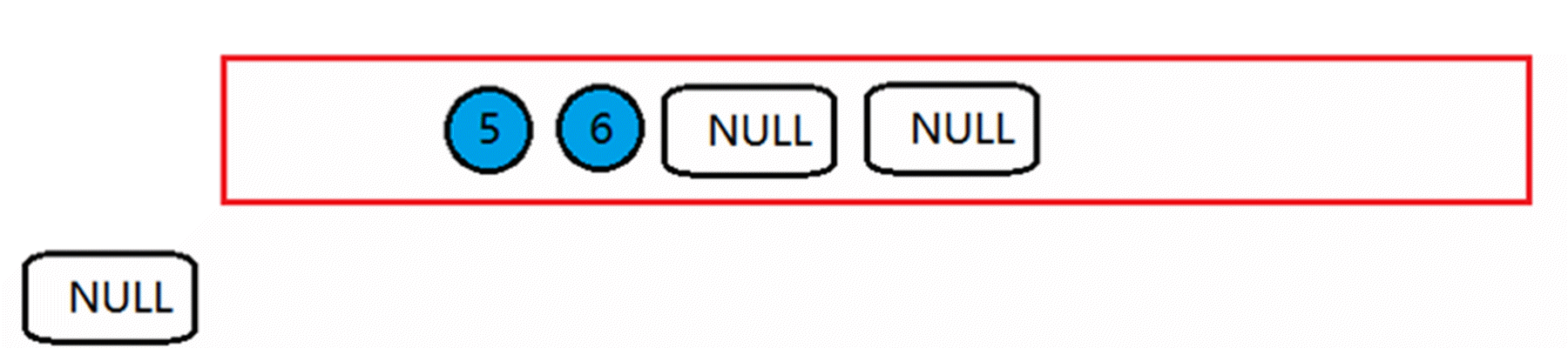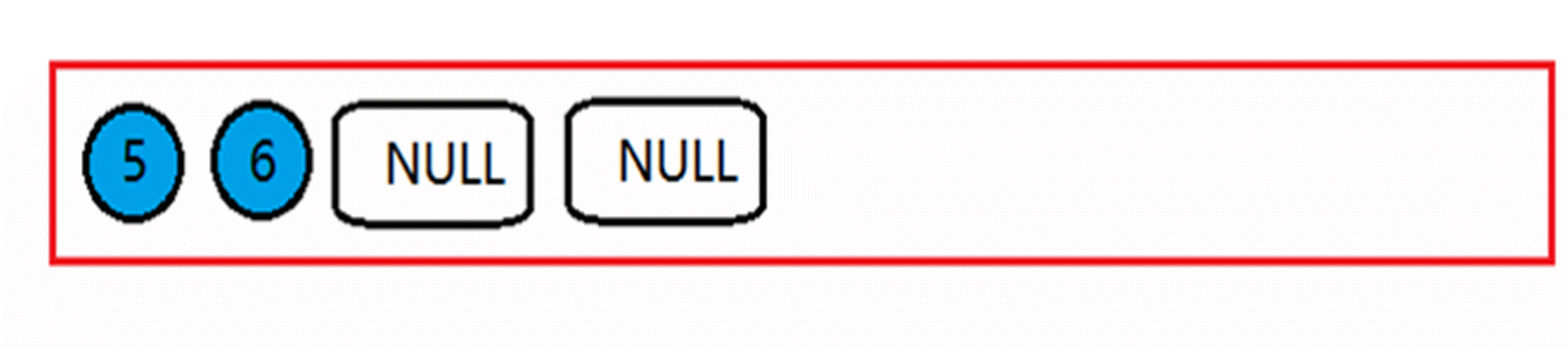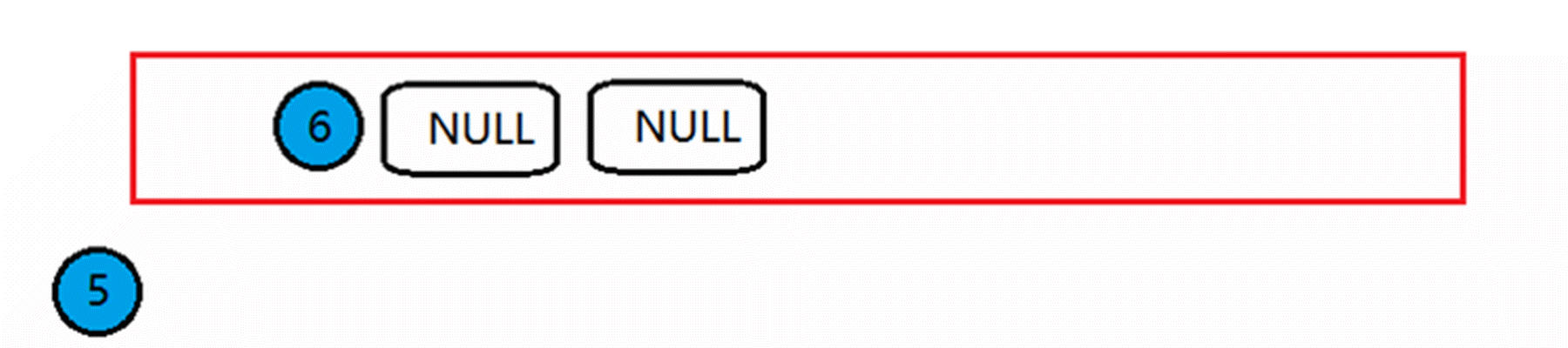
然后开始将队首的NULL出队列，重复操作，在队列中所有元素出完之前，如果有一个元素不是NULL，说明是非完全二叉树，如果都出完了并且都是NULL说明是完全二叉树。
代码实现：
bool BinaryTreeComplete(BTNode* root)
{
assert(root);
Queue q;
QueueInit(&q);//队列初始化
QueuePush(&q, root);//将根节点入队列
//层序遍历
while (1)
{
BTNode* Front = QueueFront(&q);//拿到队首元素
QueuePop(&q);//队首元素出队列
if (Front == NULL)
{
break;//当队首元素是NULL的时候跳出循环
}
//左右子节点入队列
QueuePush(&q, Front->left);
QueuePush(&q, Front->right);
}
//判断是否都是NULL
while (!QueueEmpty(&q))
{
BTNode* Front = QueueFront(&q);//拿到队首元素
QueuePop(&q);//队首元素出队列
if (Front != NULL)
{
QueueDestroy(&q);
return false;//有不是NULL的元素说明是非完全二叉树
}
}
//队列中剩下的全部是NULL
QueueDestroy(&q);
return true;//是完全二叉树
}
int main()
{
BTNode* root = CreateTree();
bool ret = BinaryTreeComplete(root);
if (ret)
printf("完全二叉树\n");
else
printf("非完全二叉树\n");
return 0;
}
举列中的二叉树确实不是完全二叉树。
将例子中的二叉树改为上图中的完全二叉树，再看运行结果。
同样是符合结果的。
选择题
题中说明这是完全二叉树，所以逆着层序的顺序还原二叉树
按照前序遍历的顺序打印出来，就是A B D H E C F G，所以答案是A。
前序遍历的第一个值就是根节点，中序遍历的中间值是根节点，所以根节点是E，答案是A。
- 后序遍历的结果是 b d e c a，所以根节点就是a，
- 又有中序遍历的结果是b a d c e，所以a的左子树只有b
- 再看后序遍历中倒数第二个的结果是c，所以a的右子树的根节点就是c
- 又因为中序遍历的第一个结果是e，所以c的右子树的根节点就是e
- 那么剩下的d就是c左子树的根节点
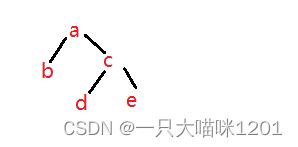
所以这个二叉树的结构是这样的，前序遍历的结果就是a b c d e，答案是D。
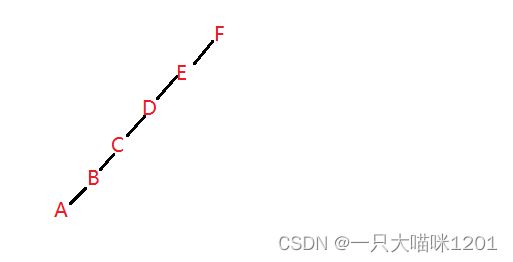
- 后序遍历中最后一个值是F，所以根节点是F
- 又因为前序遍历也是这个结果，锁门F没有右子树
- 再看倒数第二个值是E，说明E是F左子树的根节点
- 如此反复，就可以得出二叉树的结构
按照层序遍历结果是E F D C B A，答案是A。