算法60天-Day24：回溯啊，退一步海阔天空。
代码随想录（截图自参考【1】）
本系列是代码随想录算法训练营的学习笔记之day24，主要记录一下刷题的过程，以及核心知识点和一些值的记录的问题。
代码随想录的资源可以看参考链接【1】。
今日知识点
回溯算法
- 回溯法也可以叫做回溯搜索法，它是一种搜索的方式，比如在二叉树的搜索中，到叶子节点了之后我们再回到上一层；
- 回溯法的本质是穷举；
- 回溯法适合解决的问题有：
- 组合：N个数里面按一定规则找出k个数的集合
- 切割：一个字符串按一定规则有几种切割方式
- 子集：一个N个数的集合里有多少符合条件的子集
- 排列：N个数按一定规则全排列，有几种排列方式
- N皇后，解数独等等
- 说白了就是看起来只能用暴力解法的问题可以考虑下。。
模版
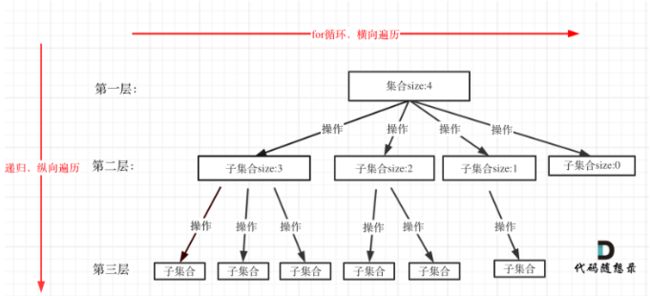
回溯法解决的问题都是在集合中递归查找子集，集合的大小构成了树的宽度，递归的深度构成树的深度。 因此，与递归类似，回溯法的三个步骤如下：
- 回溯函数模板返回值以及参数
- 终止条件
- 遍历过程（如下图）（单层搜索过程）
最重要的如何将for和递归结合起来，这样子就做到了对一棵树的横向遍历和纵向遍历。写了一个python模版：
def backtracking(参数)：
if （终止条件）：
保存结果
return
for （）：
处理节点
backtracking（）
回溯，撤销处理结果
今日题目
- 组合（77）
给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。 你可以按 任何顺序 返回答案。
来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/trim-a-binary-search-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
解题思路
- 思路就是下面这张图，脑海里要构造出树：
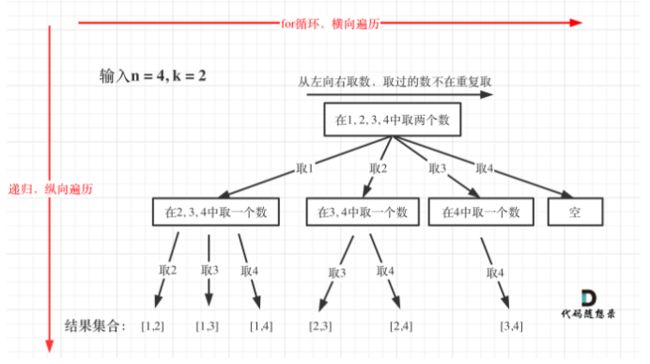
根据上图不难写出下面的代码：
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
re = []
path = []
def backtracking(n,k,index):
if len(path)==k:
re.append(path[:])
return
for i in range(index,n+1):
path.append(i)
backtracking(n,k,i+1)
path.pop()
backtracking(n,k,1)
return re
- 上面的代码相当于说是做了一个暴力搜索，遍历了全部的可能情况，但是在实际上处理的时候，有些情况下是可以提前停止，也就是进行剪枝的优化，剪枝后的代码如下：
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
re=[]
path=[]
def backtrack(n,k,startIndex):
if len(path) == k:
re.append(path[:])
return
for i in range(startIndex,n-(k-len(path))+2): #优化的地方
path.append(i) #处理节点
backtrack(n,k,i+1) #递归
path.pop() #回溯，撤销处理的节点
backtrack(n,k,1)
return re
今日思考
- 为什么剪枝的时候其边界条件是range(startIndex,n-(k-len(path))+2)？
在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历，但是range函数是左开右闭的，所以要再➕1才能取到这个值。
参考
【1】代码随想录：https://programmercarl.com/
本文由 mdnice 多平台发布