sort(a,a+m，greater＜node＞())； 记录负数情况处理数组下标；gcd(b,a%b)；全局最优可能要舍弃局部最优

Burglar and Matches

题目链接

#include
#include
#include 
#include
//#include 
using namespace std;
//const int MAX=2*1e8+5;
//int dp[MAX];//还可以拿i盒火柴能拿到的最大火柴数 
struct node{
	int x;//每个容器x个火柴盒 
	int y;//每个盒子火柴数字量
	bool operator<(const node& n)const{
		if(y==n.y)return x<n.x;
		return y<n.y;
	} 
	bool operator>(const node& n)const{
		if(y==n.y)return x>n.x;
		return y>n.y;
	} 
}a[25];
bool cmp(node n1,node n2){
	return n1.y>n2.y; 
} 
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=m;i++){//m个容器 
		cin>>a[i].x>>a[i].y;
	}
	sort(a,a+n,greater<node>());
	//sort(a,a+m,cmp);
int cnt=0;
	for(int i=0;i<m;i++){
		if(n>=a[i].x){
			cnt+=a[i].x*a[i].y;
			n-=a[i].x;
		}
		else{
			cnt+=n*a[i].y;
			break;
		}
	}
	cout<<cnt;
    return 0;
}

仰天大哭 TT

讲讲运算符重载

1、对于algorithm里的sort函数，有第三个参数 是规定排序规则的
之前熟悉的是自己定义的cmp函数
最近看了STL想用运算符重载，结果就 懵的一批

经过疯狂提交测试，

单单重载>再sort(a,a+m); 就报这种天杀的错

	bool operator>(const node& n)const{
		if(y==n.y)return x>n.x;
		return y>n.y;
	} 
	……
	sort(a,a+m);

可以选择搭配 sort(a,a+m，greater());
有点像STL里的比如map，priority_queue容器自动排序
priority_queue大顶堆
map根据键值排序

	bool operator>(const node& n)const{
		if(y==n.y)return x>n.x;
		return y>n.y;
	} 
	……
	sort(a,a+m，greater<node>());
	

如果同时重载 > 和 < ,那么直接sort(a,a+m);倒是不会出什么编译错误，只是默认按升序排列了
更新：
好叭，我又遇见了这个错误，之前搞错了。这次的问题是重载了<,但是用了小顶堆，priority_queueQ;又报了图片中可怕的错误。经过测试，这次的结论是：当使用sort，map，priority_queue这些默认自定排序的容器或者函数时，如果自己写了运算符重载，一定要按照它们自动排序的依据。比如，sort默认升序，就是要用到小于号，必须要重载小于号，再比如小顶堆，priority_queueQ;大的把小的推上去，需要用到比较符>,如果只是重载了小于号就会报错，可以单单重载大于号，也就是写一个运算符重载函数并不会改变默认排序顺序，需要自己加参数，比如sort的第三个参数greater（），而根据其默认排序规则，一定要定义该排序规则。有一个小技巧，比如sort默认按小于号排序，一定要对小于号进行运算符重载，但如果我们想将其降序排列，可以加上第三个参数再重载大于号，也可以偷懒不加参数，直接在重载小于号规则时内容改为大于号的规则

	bool operator<(const node& n)const{
		if(len==n.len)return cost>n.cost;
		else return len>n.len; 
	}
priority_queue<node> Q;
上下两种组合都是小顶堆
bool operator>(const node& n)const{
		if(len==n.len)return cost<n.cost;
		else return len<n.len; 
	}
}; 
priority_queue<node, vector<node> ,greater<node> >Q;

2、
sort( a,a+len);
这个len我一直把m搞错成n，拜托这里数组长度是m，眼睛也看不到
3、一开始手一哆嗦就想写dp，先开了个巨大的数组
const int MAX=2*1e8+5;
int dp[MAX];//还可以拿i盒火柴能拿到的最大火柴数
否掉之后，觉得声明没什么大碍，就 Memory Limit Exceed了 TT

Goldbach’s Conjecture

一个偶数总能分解成两个质因数，如果很多种分解方式，输出相差最大的两个加数

#include
#include
#include
#include
using namespace std;
//int a[1000005];//全局变量初始0 
bool isprime(int x){
	int p=(int)sqrt((double)x)+1;
	for(int i=2;i<=p;i++){
		if(x%i==0)return false;
	}
	return true;
}
int main(){
//	ios::sync_with_stdio(false);
//	cin.tie(0);
//	for(int i=3;i<1000000;i+=2){
//		if(isprime(i))a[i]=1;
//	}
	int n;//一个偶数分解成奇数的质数 
	scanf("%d",&n);
	while(n){
		for(int i=3;i<=n/2;i+=2){
			if(isprime(i)&&isprime(n-i)){
//				cout<
				printf("%d = %d + %d\n",n,i,n-i);
				break;
			}
		} 
		scanf("%d",&n);
	}
    return 0;
}

先判断了前一百万个数是否是奇的质数并存在数组里，后面直接到数组查就行，TLE了
还是 来了一个数再判断两个加数，万一来很多次输入呢 不是很服
还有，下次拜托相信
ios::sync_with_stdio(false);
cin.tie(0);

Balance

钩子分布在坐标轴上坐标已知有正有负（在平衡点原点两端），一系列重物全部要挂上去保证平衡，问平衡的挂法（//对于w[i]从a数组中选几个系数，使得相加为0（求余为0）
为了规避负数，不管是取模还是取绝对值都不行的
余数为0的状态是有余数为非零数的状态递推过来的，
用秋雨的方法会打乱 余数为非零数的状态，负的和正的混在一块儿了
最大力矩 202015，对于相加和为负数的情况也要记录下来，不存在负数下标就把下标普遍增大7500
状态递推类比 糖果 那题，这种想法特别通
若某种状态存在，能通过这种状态推出哪种状态

#include
#include
#include 
#include
#include
#include
using namespace std;
int a[25];
int w[25];
int dp[25][15000];
//对于前i个数(搭配系数)相加和为j的情况 存在几种,由于和有正有负，
//不存在负的下标，对一个很大的数字求余 
//const int mod=100000;
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
//必须用上所有重物,有几种平衡方法，不一定用上所有钩子 
	int m,n;
	cin>>m>>n;
	for(int i=1;i<=m;i++){
		cin>>a[i];//钩子距离平衡点的距离 
	}
	for(int i=1;i<=n;i++){
		cin>>w[i];//重物的重量 
	} 
	memset(dp,0,sizeof(dp));
	dp[0][7500]=1;//不挂重物 
	//对于w[i]从a数组中选几个系数，使得相加为0（求余为0） 
	for(int i=1;i<=n;i++){
		for(int j=0;j<=15000;j++){//有下面那条判断，j大于7500才会利用1进循环 
			if(dp[i-1][j])
			for(int k=1;k<=m;k++)
//			dp[i][(mod+(j+a[k]*w[i])%mod)%mod]++;
//			dp[i][abs(j+a[k]*w[i])]+=dp[i-1][j];
			dp[i][j+a[k]*w[i]]+=dp[i-1][j];
		}
	} 
//为了规避负数，不管是取模还是取绝对值都不行的
//余数为0的状态是有余数为非零数的状态递推过来的，
//用秋雨的方法会打乱 余数为非零数的状态，负的和正的混在一块儿了 
	cout<<dp[n][7500];
//cout<<-1%1000<
//cout<<1%1000<
//cout<<0%1000<
    return 0;
} 

Monitor

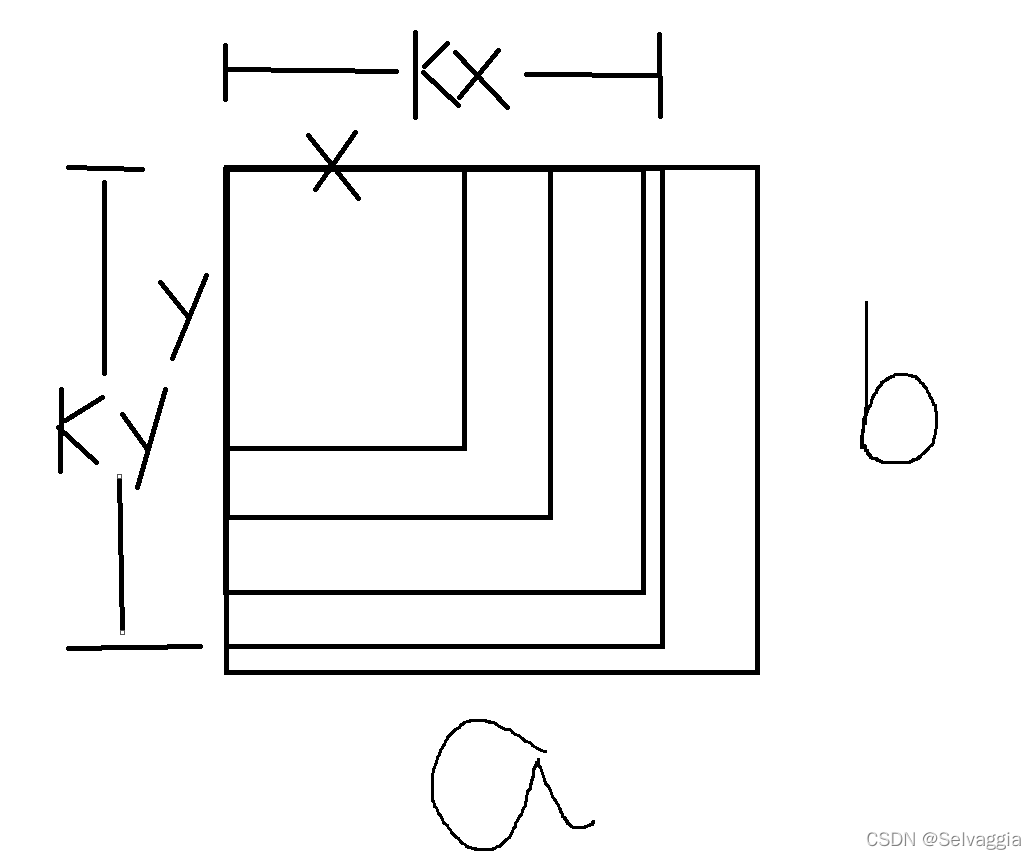
原先显示器的尺寸为a ∗ b,现在要求比例x:y, ，同时要使得显示器的面积尽可能的大,输出裁剪后的显示器

#include
#include
#include 
#include
//#include 
using namespace std;
int gcd(int a,int b){//最大公因数 
	if(a%b==0)return b;
	return gcd(b,a%b);//a%b
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	long long int a,b,x,y;//2*1e9  int也够了 
//long long 能表示19位数，无符号整数最多表示10位数的范围 
	cin>>a>>b>>x>>y;
//	int divisor=gcd(x,y);
	int divisor=__gcd(x,y);
	x/=divisor;
	y/=divisor;
	if(a<x||b<y){
		cout<<"0 0";
		return 0;
	}
	int p=a/x;
	int q=b/y;
	int ratio=min(p,q);//p,q都是大于1的，越小越接近1 
	cout<<x*ratio<<" "<<y*ratio;
    return 0;
}

Just 动态拉动一下x,y这个比例的框框，在原来ab的框架内 这个框框的哪一条边越接近ab框架，这时的面积显然最大
显然裁剪后的显示器尺寸为 kxky,显然要追求k尽量大 越接近ab框，a/kx或者是b/ky越小（越接近1啦），那么此时的k最大

Radar Installation

最少需要多少个雷达装置可以实现对海岛的全覆盖扫描

#include
#include
#include 
#include 
#include
//#include 
using namespace std;
struct node{
	double xl;
	double xr;
	bool operator <(const node& n)const{
	if(xl==n.xl)return xr<n.xr;
	return xl<n.xl;
	}
}a[1005];//每个岛受控的雷达范围，为啥要double，double=sqrt(double) 
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	int n,d;
	int t=0;
	while(cin>>n>>d){
		if(n==0&&d==0)break;
		t++;
		double x,y;
		int flag=0;
		for(int i=0;i<n;i++){
			cin>>x>>y;
			if(y>d)flag=1;
			a[i].xl=x-sqrt(d*d-y*y);
			a[i].xr=x+sqrt(d*d-y*y);
		}
		if(flag){
			cout<<"Case "<<t<<": "<<"-1"<<endl;
			continue;
		}
		sort(a,a+n);
		int cnt=1;
		int l=a[0].xl;
		int r=a[0].xr;
		for(int i=1;i<n;i++){
			if(a[i].xl>=l&&a[i].xr<=r){
				l=a[i].xl;
				r=a[i].xr;
			}
			else if(a[i].xl<r&&a[i].xr>r){
				l=a[i].xl;
			}
			else if(a[i].xl>r){
				l=a[i].xl;
				r=a[i].xr;
				cnt++;
			}
		}
		cout<<"Case "<<t<<": "<<cnt<<endl;
	} 

    return 0;
}

Human Gene Functions

给定两个碱基序列，需要输出序列间的最大相似度。

#include
#include
#include 
#include
#include
#include
#include  
using namespace std;
int dp[105][105];//s1的前i个字符与s2前j个字符最长公共序列 
int score[6][6]={{5,-1,-2,-1,-3},
                {-1,5,-3,-2,-4},
                {-2,-3,5,-2,-2},
                {-1,-2,-2,5,-1},
                {-3,-4,-2,-1,0}};
map<char,int> mp;
int get(char r,char c){
	int row=mp[r];
	int col=mp[c];
	return score[row][col];
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	mp['A']=0;mp['C']=1;mp['G']=2;mp['T']=3;mp['-']=4;
	int t;
	cin>>t;
	int len1,len2;
	string s1,s2;
//	char s1[105];
//	char s2[105];
//即便两个字符串长度不相等也没关系啦，不用考虑string后面没有字符了
//也不是真的向字符串中添加—,只不过遇到不匹配的字符时,用-与它匹配从而
//得分，也不用考虑怎么得分多，递推过程中在不断比较了 
	while(t--){
//两个字符相等得分最高，优先找公共序列 
		 cin>>len1>>s1;
		 cin>>len2>>s2;
		//scanf("%d %s",len1,s1);
		//scanf("%d %s",len2,s2);
//一上来就要用dp[i-1][j-1]，为防止越界必先初始化
memset(dp,0,sizeof(dp)); 
dp[0][0]=0;
for(int i=1;i<=len1;i++){
	dp[i][0]=get(s1[i-1],'-')+dp[i-1][0];//只能i减一咯，s1[i]拉出来比较 
} 
for(int i=1;i<=len2;i++){
	dp[0][i]=get('-',s2[i-1])+dp[0][i-1];
} 
		for(int i=1;i<=len1;i++){
			for(int j=1;j<=len2;j++){
//				if(s1[i]==s2[j])
//	dp[i][j]=max(dp[i-1][j-1]+get(s1[i-1],s2[j-1]),dp[i][j]);
//				else{
	dp[i][j]=max(dp[i][j-1]+get('-',s2[j-1]),dp[i-1][j]+get(s1[i-1],'-'));
dp[i][j]=max(dp[i-1][j-1]+get(s1[i-1],s2[j-1]),dp[i][j]);
//	dp[i][j-1]+get('-',s2[j])s1前i个和s2前j-1个假设已求出最优解，
//	s2第j个只能拉出来比较了 
//				} 
			}
		} 
		cout<<dp[len1][len2]<<endl;
	} 
    return 0;
}

1、求公共子序列呀这种设计序列里面递归的状态用以前i个字符结尾为状态

2、初始化一般（预置dp数组）一般是针对一个序列没有字符这种

3、dp数组表示的状态是前i个字符，那么dp数组是从1开始遍历的，0没有意义且已经初始化用来递推后面的情况了，请注意前i个字符对应的是str【i-1】

4、不像仅仅求公共子序列那样，分字符是否相等的情况来为dp数组赋值，不可，要考虑所有情况取最大值，相等时取到的是局部最优解，全局最优解可能要放弃这个相等的匹配的点，因此无论是否相等，都要考虑
相等匹配和放弃相等匹配与’-'匹配得到的分数

//last but node least,可能真是太罗嗦了，runtime error

都写的什么玩意儿