可视化 | 数据可视化降维算法梳理
文章目录
- 数据描述
-
- iris
- MNIST
- PCA
-
- 算法流程
- 图像描述
- Kernel-PCA
-
- 算法流程
- 图像描述
- MDS
-
- 算法流程
- 图像描述
- ISOMAP
-
- 算法流程
- 图像描述
- LLE
-
- 算法流程
- 图像描述
- LPP
-
- 算法流程
- 图像描述
- tSNE
-
- 算法流程
- 图像描述
- UMAP
-
- 算法流程
- 图像描述
本篇博客整理资源来源及代码来源,本篇主要是基于该资源,针对各种数据可视化降维算法流程梳理及可视化实践感知。
数据描述
iris
- 鸢尾花数据集收集了3种不同品种的鸢尾花(山鸢尾、变色鸢尾和维吉尼亚鸢尾)的特征数据。
- 每个样本包含了四个特征:萼片长度(sepal length)、萼片宽度(sepal width)、花瓣长度(petal length)以及花瓣宽度(petal width)。
- 数据集中的每个样本都被标记为相应的类别,即鸢尾花的品种。一共有150个样本,其中每个类别有50个样本。
MNIST
MNIST数据集是一个非常流行的手写数字图像数据库,包含了大量的手写数字图像样本。该数据集由60,000个用于训练的样本和10,000个用于测试的样本组成,每个样本都是一个28x28像素的灰度图像,并且标有相应的真实数字标签。
mnist2500_labels.txt是一个文本文件,每一行包含一个样本的标签。标签的范围是0到9,分别对应数字0到9。mnist2500_X.txt也是一个文本文件,每一行包含一个样本的特征向量。特征向量是将28x28的图像展平为一个长度为784的向量。- 每个元素表示图像中对应像素的亮度值。像素的亮度值通常用一个范围在0到1之间的数字表示,表示像素的灰度级别。
- 在这个示例中,大部分像素的值为0,表示黑色。某些像素可能具有非零值,表示该位置的像素较亮。
- 这样的一行数据包含了784个元素,分别对应原始图像中的每个像素点。读取这行数据,可以恢复出原始的28x28像素图像。每行数据都对应着MNIST数据集中的一个手写数字样本的特征向量,用于进行降维算法的练习和处理。
PCA
- PCA(Principal Component Analysis) 主成分分析
- PCA是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。
- PCA的任务:寻找一组正交基 v i v_i vi ,使所有样本沿着 v i v_i vi进行投影后,方差最大(信息量最大)
算法流程
- 加载数据集
iris:从文件中加载数据集,将特征数据和标签数据分开存储。 - 数据预处理:对特征数据进行中心化处理,即减去每个特征的平均值,使数据的均值为零。
- 计算协方差矩阵:将中心化后的特征数据计算协方差矩阵,用来描述特征之间的相关性。
- 计算特征值和特征向量:对协方差矩阵进行特征值分解,得到特征值和对应的特征向量。
- 选择特征维度:根据特征值的大小进行排序,并选取前n个最大的特征值对应的特征向量作为新的特征维度。
- 数据投影:将中心化后的特征数据投影到选取的特征维度上,得到降维后的新的数据。
- 可视化:将降维后的数据进行可视化,用散点图展示不同类别的数据在新的特征空间中的分布。
import numpy as np
import matplotlib.pyplot as plt
# 使用PCA算法进行数据降维
def pca(data, n_dim):
#N:样本数
#D:维度数
N, D = np.shape(data)
# 数据中心化处理,即将每个特征减去该特征的平均值
data = data - np.mean(data, axis=0, keepdims=True)
# 计算协方差矩阵
C = np.dot(data.T, data) / (N - 1) # [D,D]
# 计算协方差矩阵的特征值和特征向量
eig_values, eig_vector = np.linalg.eig(C)
# 对特征值进行排序,选择前n_dim个维度
# indexs_:特征值排序后的索引
indexs_ = np.argsort(-eig_values)[:n_dim]
# 选择的特征向量
picked_eig_vector = eig_vector[:, indexs_] # [D,n_dim]
# 投影数据到选取的维度上
data_ndim = np.dot(data, picked_eig_vector)
return data_ndim, picked_eig_vector
# 绘制降维后的数据图像
def draw_pic(datas, labs):
plt.cla()
# 获取唯一的标签值
unque_labs = np.unique(labs)
# 生成一系列颜色
colors = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unque_labs))]
# 散点图对象
p = []
legends = []
for i in range(len(unque_labs)):
# 找到对应标签值的数据索引
index = np.where(labs == unque_labs[i])
# 绘制散点图
pi = plt.scatter(datas[index, 0], datas[index, 1], c=[colors[i]])
p.append(pi)
legends.append(unque_labs[i])
# 添加图例
plt.legend(p, legends)
plt.show()
'''
加载鸢尾花数据集,数据集以逗号分隔,最后一列是标签。
使用PCA算法对特征进行降维,将数据降为2维。
将降维后的数据和标签传递给 draw_pic函数进行可视化。
draw_pic函数根据标签值生成不同颜色的散点图,并添加图例。
'''
if __name__ == "__main__":
# 加载鸢尾花数据集
data = np.loadtxt("iris.data", dtype="str", delimiter=',')
# 从data中提取的特征数据
feas = data[:, :-1]
feas = np.float32(feas)
# 从data中提取的标签数据
labs = data[:, -1]
# 使用PCA算法将数据降低为2维
data_2d, picked_eig_vector = pca(feas, 2)
# 绘制降维后的数据图像
draw_pic(data_2d, labs)
图像描述
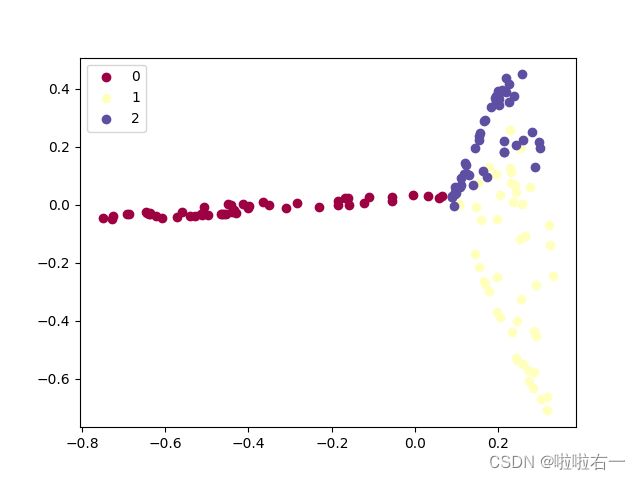
- 该散点图显示了鸢尾花数据集在降维后的两个主成分上的分布。
- 每个样本在散点图上表示为一个点,不同类别的样本用不同颜色的散点表示。
- 通过降维,我们将原始数据的多个特征降低到了两个主成分上。图中每个点的横坐标和纵坐标分别对应了数据在降维后的第一和第二个主成分上的值。
- 通过观察散点图,我们可以看到不同品种的鸢尾花在降维后的空间中形成了不同的聚类分布。这样的可视化效果有助于我们直观地了解数据集的结构和样本之间的关系
Kernel-PCA
PCA降维是一种线性变换,在高维空间的样本点如果线性不可分的话,到了低维空间依旧线性不可分。为了能够让样本在低维空间线性可分引入了KPCA(Kernel PCA)。
算法流程
输入: 数据矩阵data,降维后的维数n_dims,核函数kernel。
输出: 降维后的数据矩阵data_n。
-
计算
数据矩阵的样本个数N和特征个数D。初始化核矩阵K为一个全零矩阵。 -
对于每一个样本对
(i, j),计算核函数值K[i, j] = kernel(data[i], data[j])。 -
将核矩阵
K进行中心化操作:-
构造一个全1矩阵
one_n,其元素值均为1/N。 -
中心化操作:
K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)。
-
-
对核矩阵
K进行特征值分解,得到特征值eig_values和特征向量eig_vector。 -
对特征值进行从大到小排序,并选择前
n_dims个索引值:idx = np.argsort(-eig_values)[:n_dims]
-
提取较大的特征值和对应的特征向量:
-
eigval = eig_values[idx] -
eigvector = eig_vector[:, idx]
-
-
对特征值进行正则化处理,即将特征值开方:
eigval = eigval ** (1 / 2)
-
构建投影矩阵
u,将特征向量除以正则化后的特征值:u = eigvector / eigval.reshape(-1, n_dims)
-
将中心化后的核矩阵
K与投影矩阵u相乘,得到降维后的数据矩阵data_n:data_n = np.dot(K, u) -
返回降维后的数据矩阵
data_n。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
# a越大,输出结果的斜率越陡,非线性程度越高;r越大,输出结果偏移的程度越大。
# 定义sigmoid核函数
def sigmoid(x1, x2, a=0.25, r=1):
x = np.dot(x1, x2)
return np.tanh(a * x + r)
# 定义线性核函数
# 参数a和d控制了输入向量之间的点积运算结果的缩放和幂指数。a越大,输出结果的线性增长率越高;d越大,输出结果的幂指数增加,非线性程度越高。
# 参数c控制了输出结果的平移。增大c会使输出结果整体平移。
def linear(x1, x2, a=1, c=0, d=1):
x = np.dot(x1, x2)
x = np.power((a * x + c), d)
return x
# 定义径向基函数(RBF)核函数
# gamma参数控制了数据在降维过程中的映射范围
# 当gamma较小时,高维空间中的样本点彼此之间的相似度较高,即样本点之间的距离较远时,核函数的取值接近于0。
# 当gamma较大时,样本点之间的差异性被放大,即样本点之间的距离大的时候,核函数的取值接近于1。
def rbf(x1, x2, gamma=7):
x = np.dot((x1 - x2), (x1 - x2))
x = np.exp(-gamma * x)
return x
def kpca(data, n_dims=2, kernel=rbf):
N, D = np.shape(data)
K = np.zeros([N, N])
# 利用核函数计算K
for i in range(N):
for j in range(N):
K[i, j] = kernel(data[i], data[j])
# 对K进行中心化
one_n = np.ones((N, N)) / N
K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
# 计算特征值和特征向量
eig_values, eig_vector = np.linalg.eig(K)
idx = np.argsort(-eig_values)[:n_dims] # 从大到小排序
# 选取较大的特征值
eigval = eig_values[idx]
eigvector = eig_vector[:, idx] # [N,d]
# 进行正则化
eigval = eigval ** (1 / 2)
u = eigvector / eigval.reshape(-1, n_dims) # u [N,d]
# 进行降维
data_n = np.dot(K, u)
return data_n
def draw_pic(datas, labs):
plt.cla()
unque_labs = np.unique(labs)
colors = [plt.cm.Spectral(each)
for each in np.linspace(0, 1, len(unque_labs))]
p = []
legends = []
for i in range(len(unque_labs)):
index = np.where(labs == unque_labs[i])
pi = plt.scatter(datas[index, 0], datas[index, 1], c=[colors[i]])
p.append(pi)
legends.append(unque_labs[i])
plt.legend(p, legends)
plt.show()
if __name__ == "__main__":
iris = load_iris()
data = iris.data
labs = iris.target
data_2d = kpca(data, n_dims=2, kernel=rbf)
draw_pic(data_2d, labs)
图像描述
- 使用
kpca函数对数据进行降维操作,将数据降维为2维。这里使用了RBF(径向基函数)作为核函数。 调用draw_pic函数,将降维后的数据绘制出来。同样地,不同标签的样本用不同颜色表示。
MDS
MDS(multidimensional scaling)多维标度分析
算法流程
- 计算样本点之间的两两距离:
cal_pairwise_dist。- 获取样本数量
N和特征维度D,然后初始化一个N×N的全零矩阵dist来存储样本点之间的距离。 - 使用双重循环遍历所有样本点,并使用
np.abs函数计算两个样本点特征向量的绝对差值,然后使用np.sum函数对差值求和,得到两个样本点之间的距离,最后将距离值存入dist矩阵中。 - 最后,返回任意两个点之间的距离矩阵
dist。
- 获取样本数量
- MDS降维:
my_mds。-
获取样本数量
n,然后对距离矩阵进行处理,将小于0的距离值设为0,然后将距离值平方。 -
- 距离矩阵中所有距离值之和除以样本数量的平方,
T1 = np.ones((n, n)) * np.sum(dist) / n ** 2 - 对应样本与其他所有样本之间的距离均值,
T2 = np.sum(dist, axis=1, keepdims=True) / n - 其他所有样本与对应样本之间的距离均值,
T3 = np.sum(dist, axis=0, keepdims=True) / n B = -(T1 - T2 - T3 + dist) / 2
- 距离矩阵中所有距离值之和除以样本数量的平方,
-
使用
np.linalg.eig函数求解B矩阵的特征值和特征向量。然后对特征值进行降序排序,并选取前n_dims个特征值和对应的特征向量。将选取的特征向量乘以特征值的平方根得到降维后的数据。
-
- 绘制降维后的数据可视化图像:
draw_pic。- 获取唯一的标签值,并为每个标签值生成一个颜色。
- 遍历每个标签值,在降维后的数据中找到对应标签的索引,将这些点按照对应的颜色绘制在图上,同时记录下这些点的句柄和标签值。
- 使用
plt.legend函数设置图例,并调用plt.show函数显示图像。
import numpy as np
import matplotlib.pyplot as plt
# 计算两两样本点之间的距离
# x: 样本特征向量 [N,D]
def cal_pairwise_dist(x):
N, D = np.shape(x)
# 初始化距离矩阵
dist = np.zeros([N, N])
for i in range(N):
for j in range(N):
dist[i, j] = np.sum(np.abs(x[i] - x[j])) # 计算两个样本点之间的距离,使用绝对值和求和
# 返回任意两个点之间的距离矩阵
return dist
# 执行MDS算法,实现降维
# dist: 距离矩阵,N*N
# n_dims: 降维后的维度
# 返回降维后的数据
def my_mds(dist, n_dims):
n, n = np.shape(dist)
dist[dist < 0] = 0
dist = dist ** 2
T1 = np.ones((n, n)) * np.sum(dist) / n ** 2 # 构造T1矩阵
T2 = np.sum(dist, axis=1, keepdims=True) / n # 计算T2矩阵
T3 = np.sum(dist, axis=0, keepdims=True) / n # 计算T3矩阵
B = -(T1 - T2 - T3 + dist) / 2 # 计算B矩阵
eig_val, eig_vector = np.linalg.eig(B) # 求解B矩阵的特征值和特征向量
index_ = np.argsort(-eig_val)[:n_dims] # 对特征值进行降序排序,并选取前n_dims个特征值的索引
picked_eig_val = eig_val[index_].real # 选取特征值,并转为实数
picked_eig_vector = eig_vector[:, index_] # 选取特征向量
return picked_eig_vector * picked_eig_val ** (0.5) # 返回降维后的数据
# 绘制降维后的数据可视化图像
def draw_pic(datas, labs):
plt.cla()
unque_labs = np.unique(labs) # 获取唯一的标签值
colors = [plt.cm.Spectral(each)
for each in np.linspace(0, 1, len(unque_labs))] # 生成颜色数组,用于不同的标签类型
p = []
legends = []
for i in range(len(unque_labs)):
index = np.where(labs == unque_labs[i]) # 找到对应标签的索引
pi = plt.scatter(datas[index, 0], datas[index, 1], c=[colors[i]]) # 根据索引绘制散点图,并使用对应的颜色
p.append(pi) # 记录绘制的散点图句柄
legends.append(unque_labs[i]) # 记录标签
plt.legend(p, legends) # 设置图例
plt.show() # 显示图像
if __name__ == "__main__":
# 加载数据
data = np.loadtxt("iris.data", dtype="str", delimiter=',')
feas = data[:, :-1] # 特征部分
feas = np.float32(feas) # 将特征部分转换为浮点型
labs = data[:, -1] # 标签部分
# 计算两两样本之间的距离矩阵
dist = cal_pairwise_dist(feas)
# 进行降维
data_2d = my_mds(dist, 2) # 降到2维
# 绘制可视化图像
draw_pic(data_2d, labs)
图像描述
- 散点图的每个点表示一个样本,其中x轴和y轴分别表示降维后的第一维和第二维。不同种类的鸢尾花样本被用不同的颜色进行标记。
- 不同种类的鸢尾花样本在二维图像中可能会呈现出明显的聚类分布。
- 不同种类的鸢尾花样本在二维图像中可能会有一定的重叠区域。虽然MDS算法降维后尽可能保留了样本间的距离关系,但是仍然存在维度丢失的情况,因此不同种类的鸢尾花样本可能在某些区域发生重叠。
- 样本点之间可能存在一些异常值或离群点。这些点可能是由于数据的噪声或采样误差引起的。它们在降维后的图像中可能位于孤立的位置,远离其他样本点。
ISOMAP
ISOMAP等距特征映射
算法流程
-
在 main 函数中,首先使用
make_s_curve函数生成一个 S 曲线形状的数据集 X 和对应的标签 Y,并调用scatter_3d函数将其可视化。 -
调用
cal_pairwise_dist函数计算样本之间的距离矩阵 dist。 -
调用
my_mds函数对距离矩阵 dist 进行多维尺度变换,将高维的数据降到2维,并使用散点图绘制降维后的结果。 -
使用
my_Isomap函数对距离矩阵 dist 进行 ISOMAP 算法,将数据降到2维,并使用散点图绘制降维后的结果。def my_Isomap(D, n=2, n_neighbors=30): D_floyd = floyd(D, n_neighbors) data_n = my_mds(D_floyd, n_dims=n) return data_n -
使用 sklearn 中的 Isomap 函数对数据进行 ISOMAP 降维,同样绘制降维后的结果。
-
展示绘制的三张图。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_s_curve
from sklearn.manifold import Isomap
from tqdm import tqdm
# x 维度 [N,D]
def cal_pairwise_dist(x):
N, D = np.shape(x)
dist = np.zeros([N, N])
for i in range(N):
for j in range(N):
# dist[i,j] = np.dot((x[i]-x[j]),(x[i]-x[j]).T)
dist[i, j] = np.sqrt(np.dot((x[i] - x[j]), (x[i] - x[j]).T))
# dist[i,j] = np.sum(np.abs(x[i]-x[j]))
# 返回任意两个点之间距离
return dist
# 构建最短路径图
def floyd(D, n_neighbors=15):
Max = np.max(D) * 1000
n1, n2 = D.shape
k = n_neighbors
D1 = np.ones((n1, n1)) * Max
D_arg = np.argsort(D, axis=1)
for i in range(n1):
D1[i, D_arg[i, 0:k + 1]] = D[i, D_arg[i, 0:k + 1]]
for k in tqdm(range(n1)):
for i in range(n1):
for j in range(n1):
if D1[i, k] + D1[k, j] < D1[i, j]:
D1[i, j] = D1[i, k] + D1[k, j]
return D1
def my_mds(dist, n_dims):
# dist (n_samples, n_samples)
dist = dist ** 2
n = dist.shape[0]
T1 = np.ones((n, n)) * np.sum(dist) / n ** 2
T2 = np.sum(dist, axis=1) / n
T3 = np.sum(dist, axis=0) / n
B = -(T1 - T2 - T3 + dist) / 2
eig_val, eig_vector = np.linalg.eig(B)
index_ = np.argsort(-eig_val)[:n_dims]
picked_eig_val = eig_val[index_].real
picked_eig_vector = eig_vector[:, index_]
return picked_eig_vector * picked_eig_val ** (0.5)
def my_Isomap(D, n=2, n_neighbors=30):
D_floyd = floyd(D, n_neighbors)
data_n = my_mds(D_floyd, n_dims=n)
return data_n
def scatter_3d(X, y):
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y, cmap=plt.cm.hot)
ax.view_init(10, -70)
ax.set_xlabel("$x_1$", fontsize=18)
ax.set_ylabel("$x_2$", fontsize=18)
ax.set_zlabel("$x_3$", fontsize=18)
plt.show(block=False)
if __name__ == "__main__":
X, Y = make_s_curve(n_samples=500,
noise=0.1,
random_state=42)
scatter_3d(X, Y)
# 计算距离
dist = cal_pairwise_dist(X)
# MDS 降维
data_MDS = my_mds(dist, 2)
plt.figure()
plt.title("my_MSD")
plt.scatter(data_MDS[:, 0], data_MDS[:, 1], c=Y)
plt.show(block=False)
# ISOMAP 降维
data_ISOMAP = my_Isomap(dist, 2, 10)
plt.figure()
plt.title("my_Isomap")
plt.scatter(data_ISOMAP[:, 0], data_ISOMAP[:, 1], c=Y)
plt.show(block=False)
data_ISOMAP2 = Isomap(n_neighbors=10, n_components=2).fit_transform(X)
plt.figure()
plt.title("sk_Isomap")
plt.scatter(data_ISOMAP2[:, 0], data_ISOMAP2[:, 1], c=Y)
plt.show(block=False)
plt.show()
图像描述
-
my_Isomap:使用 ISOMAP 算法将数据降到2维后的结果,同样展示了数据在2维空间中的分布情况。与 my_MSD 图进行对比可以看出两种降维方法的差异。

-
sk_Isomap:使用 sklearn 中的 Isomap 函数对数据进行降维后的结果,同样展示了数据在2维空间中的分布情况,与 my_Isomap 进行对比可以看出两种实现的一致性。

LLE
LLE(Locally Linear Embedding,局部线性嵌入)
算法流程
- 在 main 函数中,首先使用
make_swiss_roll函数生成一个瑞士卷形状的数据集 X 和对应的标签 Y,并调用scatter_3d函数将其可视化。 - 使用LLE函数对数据集 X 进行局部线性嵌入降维,将高维的数据降到2维,并使用散点图绘制降维后的结果。
- 接收输入参数:
- data: 高维数据,格式为 [N, D],其中 N 是样本数量,D 是特征维度。
- n_dims: 降维后的目标维度。
- n_neighbors: K 近邻的数目。
- 根据输入数据计算临近点索引:
- 调用 get_n_neighbors 函数,传入数据 data 和 n_neighbors,获取每个样本点的 n_neighbors 个临近点的位置索引。
- 计算重构权重 w:
- 初始化一个全零矩阵 w,形状为 [N, n_neighbors]。
- 遍历样本集中的每个样本 i:
- 获取样本 i 的临近点数据 X_k,形状为 [n_neighbors, D],和样本 i 自身数据 X_i,形状为 [1, D]。
- 构建矩阵 I,形状为 [n_neighbors, 1],元素都为 1。
- 计算重构误差矩阵 S i = ( I ∗ X i − X k ) ∗ ( I ∗ X i − X k ) . T Si = (I * X_i - X_k) * (I * X_i - X_k).T Si=(I∗Xi−Xk)∗(I∗Xi−Xk).T。
- 为了避免对角线元素过小,加上一个非零的扰动项 t o l ∗ n p . t r a c e ( S i ) tol * np.trace(Si) tol∗np.trace(Si)。
- 使用伪逆函数 np.linalg.pinv 计算 Si 的伪逆矩阵 Si_inv。
- 计算重构权重 w [ i ] = ( I . T ∗ S i i n v ) / ( I . T ∗ S i i n v ∗ I ) w[i] = (I.T * Si_inv) / (I.T * Si_inv * I) w[i]=(I.T∗Siinv)/(I.T∗Siinv∗I)。
- 构建权重矩阵 W:
- 初始化一个全零矩阵 W,形状为 [N, N]。
- 遍历样本集中的每个样本 i,将 w[i] 中的权重值赋给 W[i] 对应的临近点索引。
- 构建对称矩阵 C:
- 计算矩阵 I_N = np.eye(N),形状为 [N, N]。
- 计算差异矩阵 C = ( I N − W ) . T ∗ ( I N − W ) C = (I_N - W).T * (I_N - W) C=(IN−W).T∗(IN−W)。
- 进行特征值分解:
- 使用 np.linalg.eig 函数计算差异矩阵 C 的特征值 eig_val 和特征向量 eig_vector。
- 选择特征值和特征向量:
- 对特征值 eig_val 进行排序,得到升序排列的索引 index_。
- 选择索引为 1 到 n_dims+1 的特征向量 eig_vector[:, index_],作为降维后的数据。
- 返回降维后的数据 y。
- 接收输入参数:
- 使用 sklearn 中的LLE函数对数据进行 LLE 降维,同样绘制降维后的结果。
- 可视化。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_swiss_roll
from sklearn.manifold import LocallyLinearEmbedding
# x 维度 [N,D]
def cal_pairwise_dist(x):
N, D = np.shape(x)
dist = np.zeros([N, N])
for i in range(N):
for j in range(N):
dist[i, j] = np.sqrt(np.dot((x[i] - x[j]), (x[i] - x[j]).T))
# 返回任意两个点之间距离
return dist
# 获取每个样本点的 n_neighbors个临近点的位置
def get_n_neighbors(data, n_neighbors=10):
dist = cal_pairwise_dist(data)
dist[dist < 0] = 0
N = dist.shape[0]
Index = np.argsort(dist, axis=1)[:, 1:n_neighbors + 1]
return Index
# data : N,D
def lle(data, n_dims=2, n_neighbors=10):
N, D = np.shape(data)
if n_neighbors > D:
tol = 1e-3
else:
tol = 0
# 获取 n_neighbors个临界点的位置
Index_NN = get_n_neighbors(data, n_neighbors)
# 计算重构权重
w = np.zeros([N, n_neighbors])
for i in range(N):
X_k = data[Index_NN[i]] # [k,D]
X_i = [data[i]] # [1,D]
I = np.ones([n_neighbors, 1])
Si = np.dot((np.dot(I, X_i) - X_k), (np.dot(I, X_i) - X_k).T)
# 为防止对角线元素过小
Si = Si + np.eye(n_neighbors) * tol * np.trace(Si)
Si_inv = np.linalg.pinv(Si)
w[i] = np.dot(I.T, Si_inv) / (np.dot(np.dot(I.T, Si_inv), I))
# 计算 W
W = np.zeros([N, N])
for i in range(N):
W[i, Index_NN[i]] = w[i]
I_N = np.eye(N)
C = np.dot((I_N - W).T, (I_N - W))
# 进行特征值的分解
eig_val, eig_vector = np.linalg.eig(C)
index_ = np.argsort(eig_val)[1:n_dims + 1]
y = eig_vector[:, index_]
return y
def scatter_3d(X, y):
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y, cmap=plt.cm.hot)
ax.view_init(10, -70)
ax.set_xlabel("$x_1$", fontsize=18)
ax.set_ylabel("$x_2$", fontsize=18)
ax.set_zlabel("$x_3$", fontsize=18)
plt.show(block=False)
if __name__ == "__main__":
X, Y = make_swiss_roll(n_samples=500)
scatter_3d(X, Y)
data_2d = lle(X, n_dims=2, n_neighbors=12)
print(data_2d.shape)
plt.figure()
plt.title("my_LLE")
plt.scatter(data_2d[:, 0], data_2d[:, 1], c=Y, cmap=plt.cm.hot)
plt.show(block=False)
data_2d_sk = LocallyLinearEmbedding(n_components=2, n_neighbors=12).fit_transform(X)
plt.figure()
plt.title("my_LLE_sk")
plt.scatter(data_2d[:, 0], data_2d[:, 1], c=Y, cmap=plt.cm.hot)
plt.show()
图像描述
LPP
- LPP(Locality Preserving Projections)局部保留投影算法
- LPP 可以被看做是PCA(Principal component analysis)的替代,同时与LE (Laplacian eigenmaps)及 LLE(Locally Linear Embedding)有着非常相近的性质。
- 计算流程与PCA类似,PCA只考虑数据本身的分布,LPP还考虑了样本点间的相对位置关系。
算法流程
- 调用
cal_pairwise_dist函数计算样本之间的欧氏距离矩阵 dist。 - 计算 dist 的最大值
max_dist。 - 分别调用LLP函数和 PCA 函数对数据 X 进行降维。LLP:
- 接收输入参数:
X: 高维数据,格式为 [N, D],其中 N 是样本数量,D 是特征维度。n_dims: 降维后的目标维度。n_neighbors: K 近邻的数目。t: 权重计算的参数。
- 计算 RBF 距离矩阵:
- 调用
cal_rbf_dist函数,传入数据 X、n_neighbors 和 t,计算 RBF 距离矩阵 W。 - 根据欧氏距离计算出的样本间距离矩阵 dist,通过 RBF 核函数计算得到 W。
- 调用
- 构建度矩阵 D:
- 初始化一个全零矩阵 D,形状与 W 相同。
- 对于每个样本 i,计算 W[i] 中非零元素的和,并将结果保存在对应的 D[i, i] 位置上。
- 构建拉普拉斯矩阵 L:
- 初始化一个全零矩阵 L,形状与 W 相同。
- 遍历样本集中的每个样本 i,计算$ L[i, j] = D[i, i] - W[i, j]$,其中 j 是样本 i 的 K 近邻。
- 计算矩阵乘积 XDXT 和 XLXT:
- X . T X.T X.T 是 X 的转置矩阵。
- X D X T = X . T ∗ D ∗ X XDXT = X.T * D * X XDXT=X.T∗D∗X,计算出的结果形状为 [D, D]。
- X L X T = X . T ∗ L ∗ X XLXT = X.T * L * X XLXT=X.T∗L∗X,计算出的结果形状为 [D, D]。
- 对矩阵 XLXT 进行特征值分解:
- 使用
np.linalg.pinv函数计算矩阵 XDXT 的伪逆。 - 将 XDXT 的伪逆与 XLXT 相乘,并利用
np.linalg.eig函数计算得到特征值 eig_val 和特征向量 eig_vec。
- 使用
- 对特征值排序和选择:
- 对特征值 eig_val 进行绝对值排序,得到排序后的索引 sort_index_。
- 根据排序后的索引 sort_index_,选择前 n_dims 个非零特征值,即从下标 j 开始取值。
- 获取降维后的数据 Y:
- 根据所选的特征值索引 sort_index_,获取相应的特征向量 eig_vec。
- 将特征向量 eig_vec 与原始数据 X 相乘,得到降维后的数据 Y,其形状为 [N, n_dims],其中 N 是样本数量。
- 接收输入参数:
- 使用不同的子图显示 LPP 降维结果和 PCA 降维结果的散点图,并根据原始的目标变量 Y 进行着色。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
# x 维度 [N,D]
def cal_pairwise_dist(X):
N, D = np.shape(X)
tile_xi = np.tile(np.expand_dims(X, 1), [1, N, 1])
tile_xj = np.tile(np.expand_dims(X, axis=0), [N, 1, 1])
dist = np.sum((tile_xi - tile_xj) ** 2, axis=-1)
# 返回任意两个点之间距离
return dist
def rbf(dist, t=1.0):
'''
rbf kernel function
'''
return np.exp(-(dist / t))
def cal_rbf_dist(data, n_neighbors=10, t=1):
dist = cal_pairwise_dist(data)
dist[dist < 0] = 0
N = dist.shape[0]
rbf_dist = rbf(dist, t)
W = np.zeros([N, N])
for i in range(N):
index_ = np.argsort(dist[i])[1:1 + n_neighbors]
W[i, index_] = rbf_dist[i, index_]
W[index_, i] = rbf_dist[index_, i]
return W
# X 输入高维数据 格式 [N,D]
# n_neighbors K近邻的数目
# t 权重计算的参数
def lpp(X, n_dims=2, n_neighbors=30, t=1.0):
N = X.shape[0]
W = cal_rbf_dist(X, n_neighbors, t)
D = np.zeros_like(W)
for i in range(N):
D[i, i] = np.sum(W[i])
L = D - W
XDXT = np.dot(np.dot(X.T, D), X)
XLXT = np.dot(np.dot(X.T, L), X)
eig_val, eig_vec = np.linalg.eig(np.dot(np.linalg.pinv(XDXT), XLXT))
sort_index_ = np.argsort(np.abs(eig_val))
eig_val = eig_val[sort_index_]
print("eig_val[:10]", eig_val[:10])
j = 0
while eig_val[j] < 1e-6:
j += 1
print("j: ", j)
sort_index_ = sort_index_[j:j + n_dims]
eig_val_picked = eig_val[j:j + n_dims]
print(eig_val_picked)
A = eig_vec[:, sort_index_]
Y = np.dot(X, A)
return Y
def scatter_3d(X, y):
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y, cmap=plt.cm.hot)
ax.view_init(10, -70)
ax.set_xlabel("$x_1$", fontsize=18)
ax.set_ylabel("$x_2$", fontsize=18)
ax.set_zlabel("$x_3$", fontsize=18)
plt.show(block=False)
if __name__ == '__main__':
X = load_iris().data
Y = load_iris().target
n_neighbors = 5
dist = cal_pairwise_dist(X)
max_dist = np.max(dist)
data_2d_LPP = lpp(X, n_neighbors=n_neighbors, t=0.01 * max_dist)
data_2d_PCA = PCA(n_components=2).fit_transform(X)
plt.figure(figsize=(12, 6))
plt.subplot(121)
plt.title("LPP")
plt.scatter(data_2d_LPP[:, 0], data_2d_LPP[:, 1], c=Y)
plt.subplot(122)
plt.title("PCA")
plt.scatter(data_2d_PCA[:, 0], data_2d_PCA[:, 1], c=Y)
plt.show()
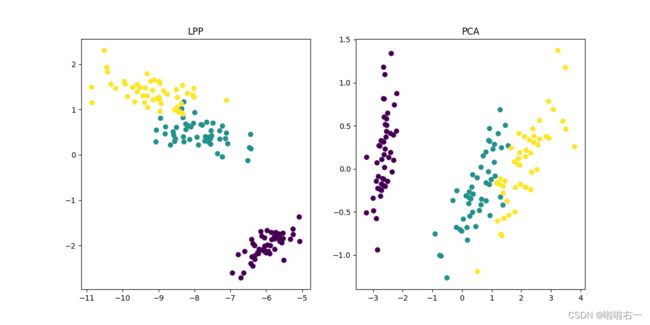
图像描述
LPP 降维:使用 LPP 算法将数据降到2维后的结果,散点图展示了数据在2维空间中的分布情况。
tSNE
- t-SNE(t-Distributed Stochastic Neighbor Embedding)
- t-sne是一种非常常用的数据降维(数据可视化)基本原理:
- 在高维空间构建一个概率分布拟合高维样本点间的相对位置关系
- 在低维空间,也构建一个概率分布,拟合低维样本点之间的位置关系
- 通过学习,调整低维数据点,令两个分布接近
算法流程
-
计算数据集中任意两点之间的距离:
cal_pairwise_dist。- 输入是一个 NxD 维度的矩阵,其中 N 是数据点的数量,D 是每个数据点的维度。
- 它首先对 X 计算平方和,然后根据欧式距离公式计算距离。
-
计算联合概率 P i j P_{ij} Pij及其对应的熵:
calc_P_and_entropy。- 根据给定的 beta 值和距离矩阵 D 来计算联合概率矩阵 P 和对应的熵
- sigma (可以由beta导出)是高斯核宽度,用于模糊相似度图。
- 函数返回归一化后的 P 矩阵和对数熵。
-
二分搜索的方法寻找最优的σ:
binary_search。- 对每个数据点执行二分搜索以找到最优的 beta 值。
- 目标是找到最优的 beta 值,使得给定点的高斯相似度的对数熵接近预设 perplexity 的对数值。
-
计算高维数据的联合概率:
p_joint。- 计算高维数据的联合概率矩阵 P。
- 首先计算所有点对的距离,然后对每个点运用二分搜索找到最优的 sigma,最后计算联合概率。
-
计算低维数据的联合概率:
q_tsne。- 根据嵌入在低维空间的点计算低维的联合概率矩阵 Q 和相应的元素num。
-
**t-SNE算法的主体部分。**首先计算高维数据的联合概率,然后进行迭代训练,更新低维数据,最后返回低维数据:
estimate_tsen- 计算高维联合概率 P,然后通过迭代优化降维嵌入 Y(低维数据 [N,d])。
- 在每一轮,它根据当前的Y 计算低维联合概率 Q,
- 然后用基于梯度下降的方法更新 Y。
-
可视化:
draw_pic。
import numpy as np
import matplotlib.pyplot as plt
from PCA import pca
# 计算任意两点之间的欧式距离 ||x_i-x_j||^2
# X 维度 [N,D],其中 N 是数据点的数量,D 是每个数据点的维度
# 首先对 X 计算平方和,然后根据欧式距离公式计算距离。
def cal_pairwise_dist(X):
sum_X = np.sum(np.square(X), 1)
D = np.add(np.add(-2 * np.dot(X, X.T), sum_X).T, sum_X)
# 返回任意两个点之间距离
return D
# 计算P_ij 以及 log松弛度
def calc_P_and_entropy(D, beta=1.0):
P = np.exp(-D.copy() * beta)
sumP = np.sum(P)
# 计算熵
log_entropy = np.log(sumP) + beta * np.sum(D * P) / sumP
P = P / sumP
return P, log_entropy
# 二值搜索寻找最优的 sigma
def binary_search(D, init_beta, logU, tol=1e-5, max_iter=50):
beta_max = np.inf
beta_min = -np.inf
beta = init_beta
P, log_entropy = calc_P_and_entropy(D, beta)
diff_log_entropy = log_entropy - logU
m_iter = 0
while np.abs(diff_log_entropy) > tol and m_iter < max_iter:
# 交叉熵比期望值大,增大beta
if diff_log_entropy > 0:
beta_min = beta
if beta_max == np.inf or beta_max == -np.inf:
beta = beta * 2
else:
beta = (beta + beta_max) / 2.
# 交叉熵比期望值小, 减少beta
else:
beta_max = beta
if beta_min == -np.inf or beta_min == -np.inf:
beta = beta / 2
else:
beta = (beta + beta_min) / 2.
# 重新计算
P, log_entropy = calc_P_and_entropy(D, beta)
diff_log_entropy = log_entropy - logU
m_iter = m_iter + 1
# 返回最优的 beta 以及所对应的 P
return P, beta
# 给定一组数据 datas :[N,D]
# 计算联合概率 P_ij : [N,N]
def p_joint(datas, target_perplexity):
N, D = np.shape(datas)
# 计算两两之间的距离
distances = cal_pairwise_dist(datas)
# beta = 1/(2*sigma^2)
beta = np.ones([N, 1])
logU = np.log(target_perplexity)
p_conditional = np.zeros([N, N])
# 对每个样本点搜索最优的sigma(beta) 并计算对应的P
for i in range(N):
if i % 500 == 0:
print("Compute joint P for %d points" % (i))
# 删除 i -i 点
Di = np.delete(distances[i, :], i)
# 进行二值搜索,寻找 beta
# 使 log_entropy 最接近 logU
P, beta[i] = binary_search(Di, beta[i], logU)
# 在ii的位置插0
p_conditional[i] = np.insert(P, i, 0)
# 计算联合概率
P_join = p_conditional + p_conditional.T
P_join = P_join / np.sum(P_join)
print("Mean value of sigma: %f" % np.mean(np.sqrt(1 / beta)))
return P_join
# Y : 低维数据 [N,d]
# 根据Y,计算低维的联合概率 q_ij
def q_tsne(Y):
N = np.shape(Y)[0]
sum_Y = np.sum(np.square(Y), 1)
num = -2. * np.dot(Y, Y.T)
num = 1. / (1. + np.add(np.add(num, sum_Y).T, sum_Y))
num[range(N), range(N)] = 0.
Q = num / np.sum(num)
Q = np.maximum(Q, 1e-12)
return Q, num
# datas 输入高维数据 [N,D]
# labs 高维数据的标签[N,1]
# dim 降维的维度 d
# plot 绘图
def estimate_tsen(datas, labs, dim, target_perplexity, plot=False):
N, D = np.shape(datas)
# 随机初始化低维数据Y
Y = np.random.randn(N, dim)
# 计算高维数据的联合概率
print("Compute P_joint")
P = p_joint(datas, target_perplexity)
# 开始若干轮对 P 进行放大
P = P * 4.
P = np.maximum(P, 1e-12)
# 开始进行迭代训练
# 训练相关参数
max_iter = 1500
initial_momentum = 0.5
final_momentum = 0.8
eta = 500 # 学习率,通常较大
min_gain = 0.01
dY = np.zeros([N, dim]) # 梯度
iY = np.zeros([N, dim]) # Y的变化
gains = np.ones([N, dim])
for m_iter in range(max_iter):
# 计算 Q
Q, num = q_tsne(Y)
# 计算梯度
PQ = P - Q
for i in range(N):
dY[i, :] = np.sum(np.tile(PQ[:, i] * num[:, i], (dim, 1)).T * (Y[i, :] - Y), 0)
# Perform the update
if m_iter < 20:
momentum = initial_momentum
else:
momentum = final_momentum
gains = (gains + 0.2) * ((dY > 0.) != (iY > 0.)) + \
(gains * 0.8) * ((dY > 0.) == (iY > 0.))
gains[gains < min_gain] = min_gain
iY = momentum * iY - eta * (gains * dY)
Y = Y + iY
# Y 去中心化,点的偏移对点和点之间的距离无影响
Y = Y - np.tile(np.mean(Y, 0), (N, 1))
# Compute current value of cost function
if (m_iter + 1) % 10 == 0:
C = np.sum(P * np.log(P / Q))
print("Iteration %d: loss is %f" % (m_iter + 1, C))
# 停止放大P
if m_iter == 100:
P = P / 4.
if plot and m_iter % 100 == 0:
print("Draw Map")
draw_pic(Y, labs, name="%d.jpg" % (m_iter))
return Y
def draw_pic(datas, labs, name='1.jpg'):
plt.cla()
unque_labs = np.unique(labs)
colors = [plt.cm.Spectral(each)
for each in np.linspace(0, 1, len(unque_labs))]
p = []
legends = []
for i in range(len(unque_labs)):
index = np.where(labs == unque_labs[i])
pi = plt.scatter(datas[index, 0], datas[index, 1], c=[colors[i]])
p.append(pi)
legends.append(unque_labs[i])
plt.legend(p, legends)
plt.savefig(name)
if __name__ == "__main__":
mnist_datas = np.loadtxt("mnist2500_X.txt")
mnist_labs = np.loadtxt("mnist2500_labels.txt")
print("first reduce by PCA")
datas, _ = pca(mnist_datas, 30)
X = datas.real
Y = estimate_tsen(X, mnist_labs, 2, 30, plot=True)
draw_pic(Y, mnist_labs, name="final.jpg")
图像描述
迭代过程
- 最后生成的 “final.jpg” 图像中,横纵坐标是原始高维度数据通过 t-SNE 算法降维到二维之后的坐标值,也就是每个数据点在二维空间中的位置。这两个坐标值是通过 t-SNE 算法根据数据点在高维空间中的相互布局关系计算得出的。
- 至于散点的颜色,每种颜色代表了一个特定的类别。
UMAP
- UMAP(Uniform Manifold Approximation and Projection)均匀流形逼近与投影
- UMAP 是新近提出的一种新型的数据降维(数据可视化)方法。其算法原理以及降维效果与t-sne类似,但有以下改进:
- 比t-sne 可以得到更好的数据聚拢效果,能能够表达更好的局部结构。
- 运算效率以及运算速度比t-sne好的多,可以适用于大规模数据降维。
- 可以实现任意维度的降维。
算法流程
-
相关函数:
- 计算样本点两两之间距离的函数
cal_pairwise_dist()。 - 获取每个样本点n_neighbors个临近点位置和距离的函数
get_n_neighbors()。 - 计算样本点参数 sigmas 和 rhos 的函数
compute_sigmas_and_rhos()。 - 计算样本点之间连接强度的函数
compute_membership_strengths()。 - 获取图输入的函数
get_graph_Inputs()。 - 使用谱分析法进行初始化的函数
init_embedding_spectral()。 - 计算每条边多少个 epoch 更新一次的函数
make_epochs_per_sample()。 - 梯度裁剪函数
clip()。 - 训练一轮的函数
train_one_epoch()。 - 通过训练获取 embedding 的函数
train_embedding()。 - 获取 embedding 的函数
get_embedding()。 - 找到参数 a 和 b 的函数
find_ab_params()。 - UMAP 算法的主要实现函数
UAMP(),依次调用上述定义的函数。 - 绘制结果图像的函数
draw_pic()。
- 计算样本点两两之间距离的函数
-
整个程序中,UMAP 算法的主要思路如下:
-
从高维数据中计算样本点之间的距离和连接关系。
-
计算 sigmas 和 rhos 参数。
-
通过谱分析方法初始化低维嵌入。
-
训练一轮微调嵌入,包括更新正样本和负样本。
-
通过多轮训练,利用梯度下降法优化降维结果。
-
最后用 matplotlib 库绘制降维结果并展示。
-
-
main函数
- 首先读取手写数字识别数据集MNIST的样本数据(“mnist2500_X.txt”)和标签数据(“mnist2500_labels.txt”),并打印出样本数据的形状。
- (2500, 784)
- 之后,程序调用UMAP函数处理样本数据,通过设置降维后的维数为2,最小距离为0.3,最大距离(spread)为2,以及邻近节点数为30,对MNIST数据进行降维处理,并将降维后的数据存储在变量
embedding中,并将降维数据的形状打印出来。这一步主要是进行降维计算。- (2500, 2)
- 调用
draw_pic()函数将降维后的数据进行可视化展示,并将可视化结果保存为"final-d0.01n-30_new.jpg"文件。这一步主要是为了展示降维的效果 - 最后,使用
plt.show()命令显示出图像。
- 首先读取手写数字识别数据集MNIST的样本数据(“mnist2500_X.txt”)和标签数据(“mnist2500_labels.txt”),并打印出样本数据的形状。
import numpy as np
from scipy.optimize import curve_fit
from tqdm import tqdm
import scipy.sparse
# 利用numba 提高运行速度
import numba
import matplotlib.pyplot as plt
from warnings import warn
# x 维度 [N,D]
def cal_pairwise_dist(x):
print("compute distance")
N,D = np.shape(x)
dist = np.zeros([N,N])
for i in tqdm(range(N)):
for j in range(N):
dist[i,j] = np.sqrt(np.dot((x[i]-x[j]),(x[i]-x[j]).T))
#返回任意两个点之间距离
return dist
# 获取每个样本点的 n_neighbors个临近点的位置以及距离
def get_n_neighbors(data, n_neighbors = 15):
dist = cal_pairwise_dist(data)
dist[dist < 0] = 0
N = dist.shape[0]
NN_index = np.argsort(dist,axis=1)[:,0:n_neighbors]
NN_dist = np.sort(dist,axis=1)[:,0:n_neighbors]
return NN_index,NN_dist
# 计算每个样本点的参数 sigmas 以及 rhos
def compute_sigmas_and_rhos(distances,k,
local_connectivity=1,n_iter=64,
tol = 1.0e-5,min_k_dis_scale=1e-3):
print("computing sigmas and rhos")
# 获取样本数目
N= distances.shape[0]
# 定义变量存储每个样本的 sigma 和 rho
rhos = np.zeros(N, dtype=np.float32)
sigmas = np.zeros(N, dtype=np.float32)
mean_distances = np.mean(distances)
target = np.log2(k)
for i in tqdm(range(N)):
lo = 0.0
hi = np.inf
mid = 1.0
# rho_i 为距离第i个样本最近的第local_connectivity个距离
ith_distances = distances[i]
non_zero_dists = ith_distances[ith_distances > 0.0]
rhos[i] = non_zero_dists[local_connectivity - 1]
# 通过2值搜索的方法计算sigma_i
for n in range(n_iter):
psum = 0.0
for j in range(1, distances.shape[1]):
d = distances[i, j] - rhos[i]
if d > 0:
psum += np.exp(-(d / mid))
else:
psum += 1.0
if np.fabs(psum - target) < tol:
break
if psum > target:
hi = mid
mid = (lo + hi) / 2.0
else:
lo = mid
if hi == np.inf:
mid *= 2
else:
mid = (lo + hi) / 2.0
sigmas[i] = mid
# 进一步处理 防止 sigma_i 过小
if rhos[i] > 0.0:
mean_ith_distances = np.mean(ith_distances)
if sigmas[i] < min_k_dis_scale * mean_ith_distances:
sigmas[i] = min_k_dis_scale * mean_ith_distances
# rhos[i]<=0 N个近邻点距离过近
else:
if sigmas[i] < min_k_dis_scale * mean_distances:
sigmas[i] = min_k_dis_scale * mean_distances
return sigmas,rhos
# 计算两点间的连接强度
def compute_membership_strengths(NN_index,NN_dists,sigmas,rhos):
print("compute membership strengths")
n_samples, n_neighbors = np.shape(NN_index)
rows = np.zeros(n_samples*n_neighbors, dtype=np.int32)
cols = np.zeros(n_samples*n_neighbors, dtype=np.int32)
vals = np.zeros(n_samples*n_neighbors, dtype=np.float32)
for i in tqdm(range(n_samples)):
for j in range(n_neighbors):
if NN_index[i, j] == i:
val = 0.0
elif NN_dists[i, j] - rhos[i] <= 0.0 or sigmas[i] == 0.0:
val = 1.0
else:
val = np.exp(-((NN_dists[i, j] - rhos[i]) / (sigmas[i])))
rows[i * n_neighbors + j] = i
cols[i * n_neighbors + j] = NN_index[i, j]
vals[i * n_neighbors + j] = val
return rows, cols, vals
def get_graph_Inputs(X,n_neighbors,local_connectivity=1):
n_samples = X.shape[0]
# 计算每个样本点的N个临近点的位置和距离
NN_index, NN_dists = get_n_neighbors(X,n_neighbors)
# 计算每个样本的 sigm 与 rho 为后边的图计算提供参数
sigmas,rhos = compute_sigmas_and_rhos(NN_dists,n_neighbors,local_connectivity)
# 计算两点间的 连接强度 即计算条件概率 Pj|i
rows, cols, vals = compute_membership_strengths(NN_index,NN_dists,sigmas,rhos)
# 构造稀疏矩阵
result = scipy.sparse.coo_matrix((vals, (rows, cols)), shape=(X.shape[0], X.shape[0]))
result.eliminate_zeros() # 去掉0
# 计算联合概率 Pij
transpose = result.transpose()
prod_matrix = result.multiply(transpose)
# Pij = Pj|i + Pi|j - Pj|i* Pi|j
result = result + transpose - prod_matrix
return result
# 谱分析法进行初始化
def init_embedding_spectral(graph,dim):
n_samples = graph.shape[0]
k = dim
diag_data = np.asarray(graph.sum(axis=0))
# Normalized Laplacian
I = scipy.sparse.identity(graph.shape[0], dtype=np.float64)
D = scipy.sparse.spdiags(
1.0 / np.sqrt(diag_data), 0, graph.shape[0], graph.shape[0]
)
L = I - D * graph * D
num_lanczos_vectors = max(2 * k + 1, int(np.sqrt(graph.shape[0])))
try:
if L.shape[0] < 2000000:
eigenvalues, eigenvectors = scipy.sparse.linalg.eigsh(
L,
k+1,
which="SM",
ncv=num_lanczos_vectors,
tol=1e-4,
v0=np.ones(L.shape[0]),
maxiter=graph.shape[0] * 5,
)
else:
print("---------------eigenvalues-------------------")
eigenvalues, eigenvectors = scipy.sparse.linalg.lobpcg(
L, np.random.normal(size=(L.shape[0], k+1)), largest=False, tol=1e-8
)
order = np.argsort(eigenvalues)[1:k+1]
return eigenvectors[:, order]
except scipy.sparse.linalg.ArpackError:
warn(
"WARNING: spectral initialisation failed! The eigenvector solver\n"
"failed. This is likely due to too small an eigengap. Consider\n"
"adding some noise or jitter to your data.\n\n"
"Falling back to random initialisation!"
)
return np.random.uniform(low=-10.0, high=10.0, size=(graph.shape[0], dim))
def make_epochs_per_sample(weights, n_epochs):
result = -1.0 * np.ones(weights.shape[0], dtype=np.float64)
# 边的权重越大在整个训练过程中更新的次数越多,更新间隔越小
n_samples = n_epochs * (weights / weights.max())
result[n_samples > 0] = float(n_epochs) / n_samples[n_samples > 0] # 更新间隔
return result
# 梯度裁剪 -4,+4之间
@numba.njit()
def clip(val):
if val > 4.0:
return 4.0
elif val < -4.0:
return -4.0
else:
return val
def train_one_epoch(head_embedding,
tail_embedding,
head,
tail,
n_vertices,
epochs_per_sample,
epochs_per_negative_sample,
epoch_of_next_sample,
epoch_of_next_negative_sample,
a,
b,
alpha,
n,
dim):
for i in range(epochs_per_sample.shape[0]):
#对正样本进行采样
if epoch_of_next_sample[i] <= n:
j = head[i]
k = tail[i]
current = head_embedding[j]
other = tail_embedding[k]
# 计算两点间距离
dist_squared = np.dot((current-other),(current-other))
# 计算正样本梯度
if dist_squared > 0.0:
grad_coeff = -2.0 * a * b * pow(dist_squared, b - 1.0)
grad_coeff /= a * pow(dist_squared, b) + 1.0
else:
grad_coeff = 0.0
# 进行更新
for d in range(dim):
# 梯度裁剪
grad_d = clip(grad_coeff * (current[d] - other[d]))
# 梯度
current[d] += grad_d * alpha
# 下次更新的轮次
epoch_of_next_sample[i] += epochs_per_sample[i]
# 计算负样本的数目
n_neg_samples = int(
(n - epoch_of_next_negative_sample[i]) / epochs_per_negative_sample[i]
)
# 进行负样本采样
for p in range(n_neg_samples):
k = np.random.randint(n_vertices)
other = tail_embedding[k]
dist_squared = np.dot((current-other),(current-other))
if dist_squared > 0.0:
grad_coeff = 2.0 * b
grad_coeff /= (0.001 + dist_squared) * (
a * pow(dist_squared, b) + 1
)
elif j == k:
continue
else:
grad_coeff = 0.0
for d in range(dim):
if grad_coeff > 0.0:
grad_d = clip(grad_coeff * (current[d] - other[d]))
else:
grad_d = 4.0
current[d] += grad_d * alpha
# 计算下次负样本更新轮次
epoch_of_next_negative_sample[i] += (
n_neg_samples * epochs_per_negative_sample[i]
)
# 通过训练获得embedding
def train_embedding(head_embedding, #头结点 向量
tail_embedding, #尾结点 向量
head, # 头结点 编号
tail, # 尾结点 编号
epochs_per_sample, # 正样本采样控制
epochs_per_negative_sample, # 负样本采样控制
a,b, #
initial_alpha, # 初始化学习率
n_epochs, # 训练轮次
n_vertices # 顶点数目
):
dim = head_embedding.shape[1]
alpha = initial_alpha
epoch_of_next_negative_sample = epochs_per_negative_sample.copy()
epoch_of_next_sample = epochs_per_sample.copy()
optimize_fn = numba.njit(train_one_epoch, fastmath=True, parallel=False)
for n in tqdm(range(n_epochs)):
# 进行1轮更新
optimize_fn(head_embedding,
tail_embedding,
head,
tail,
n_vertices,
epochs_per_sample,
epochs_per_negative_sample,
epoch_of_next_sample,
epoch_of_next_negative_sample,
a,
b,
alpha,
n,
dim)
# 更新学习率
alpha = initial_alpha * (1.0 - (float(n) / float(n_epochs)))
return head_embedding
def get_embedding(graph,
dim,a,b,
negative_sample_rate,
n_epochs=None,
initial_alpha=1.0):
# 行列交换
graph = graph.tocoo()
graph.sum_duplicates()
# 顶点数目
n_vertices = graph.shape[1]
# 计算迭代轮次 数据越少迭代轮次越多
if n_epochs is None:
if graph.shape[0] <= 10000:
n_epochs = 500
else:
n_epochs = 200
# 边的权重过低,无法采样,将权重设置为0
if n_epochs > 10:
graph.data[graph.data < (graph.data.max() / float(n_epochs))] = 0.0
graph.eliminate_zeros()
# 利用谱分析的方法,借助graph,对低维数据进行初始化
initialisation = init_embedding_spectral(graph,dim)
# 加入一些随机数据增加随机性
expansion = 10.0 / np.abs(initialisation).max()
embedding = (initialisation * expansion).astype(
np.float32
) + np.random.normal(
scale=0.0001, size=[graph.shape[0], dim]
).astype(
np.float32
)
# 计算图中每条边,每隔多少个epoch 更新一次
epochs_per_sample = make_epochs_per_sample(graph.data, n_epochs)
# 负样本,每隔多少个epoch 更新一次
epochs_per_negative_sample = epochs_per_sample/negative_sample_rate
# 开始进行训练,获取 embedding
head = graph.row
tail = graph.col
# 训练获取降维数据
embedding =train_embedding(embedding,embedding,
head,tail,
epochs_per_sample,epochs_per_negative_sample,
a,b,initial_alpha,n_epochs,n_vertices)
return embedding
def find_ab_params(min_dist,spread):
def curve(x, a, b):
return 1.0 / (1.0 + a * x ** (2 * b))
xv = np.linspace(0, spread * 3, 300)
yv = np.zeros(xv.shape)
yv[xv < min_dist] = 1.0
yv[xv >= min_dist] = np.exp(-(xv[xv >= min_dist] - min_dist) / spread)
params, covar = curve_fit(curve, xv, yv)
return params[0], params[1]
def UAMP(X,
dim=2, # 降维后的维度
n_neighbors=15, # N近邻
min_dist = 0.1, # 控制投影后,相似点的聚拢程度
spread = 1,
negative_sample_rate=5, # 负样本采样是正样本采样的多少倍
n_epochs=None, # 训练轮次
initial_alpha= 1.0 # 初始化学习率
):
# 估算参数 a,b
a,b = find_ab_params(min_dist,spread)
# 根据高维数据 计算点与点之间的连接关系
graph = get_graph_Inputs(X,n_neighbors,local_connectivity=1)
print(graph)
#
embedding = get_embedding(graph,dim,a,b,negative_sample_rate,n_epochs,initial_alpha)
return embedding
def draw_pic(datas,labs,name = '1.jpg'):
plt.cla()
unque_labs = np.unique(labs)
colors = [plt.cm.Spectral(each)
for each in np.linspace(0, 1,len(unque_labs))]
p=[]
legends = []
for i in range(len(unque_labs)):
index = np.where(labs==unque_labs[i])
pi = plt.scatter(datas[index, 0], datas[index, 1], c =[colors[i]] )
p.append(pi)
legends.append(unque_labs[i])
plt.legend(p, legends)
plt.savefig(name)
if __name__ == "__main__":
mnist_datas = np.loadtxt("mnist2500_X.txt")
mnist_labs = np.loadtxt("mnist2500_labels.txt")
print(mnist_datas.shape)
embedding = UAMP(mnist_datas,dim=2,min_dist=0.3,spread=2,n_neighbors=30)
print(embedding.shape)
draw_pic(embedding,mnist_labs,name = "final-d0.01n-30_new.jpg")
plt.show()
图像描述
- 参数设置:
dim=2,min_dist=0.01,spread=1
- 参数设置:
dim=2,min_dist=0.3,spread=2