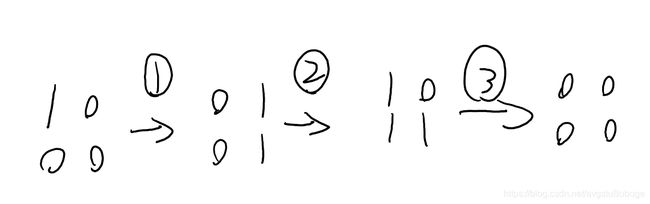Codeforces Round #684 (Div. 2) A - C2 题解

Codeforces Round #684 (Div. 2) A - C2 题解

A Buy the String

题意

给定一个长度为 $n$ 的01串，你可以用 $h$ 的代价把字符串中任意一个字符取反，最终你要把这个01串买下来，0的单价为$c_0$，1的单价为 $c_1$。现给你$n,h,c_0,c_1$以及一个01串，问你最少花多少可以买下这个串。输出最小总价。

思路

贪心，设$c_0<c_1$，若$c_1-c_0>h$，则把所有1换成0。即1的单价为$min(c_0+h,c_1)$，0的单价为$c_0$。

代码

#include 

using namespace std;

int main() {
    int T;
    cin >> T;
    while (T--) {
        int n, c0, c1, h;
        cin >> n >> c0 >> c1 >> h;
        string s;
        cin >> s;
        int ans = 0;
        if (c0 > c1) {
            for (char ch : s) {
                if (ch == '1') {
                    ans += c1;
                } else {
                    ans += min(c0, c1 + h);
                }
            }
        } else {
            for (char ch : s) {
                if (ch == '0') {
                    ans += c0;
                } else {
                    ans += min(c1, c0 + h);
                }
            }
        }
        cout << ans << '\n';
    }
    return 0;
}

B Sum of Medians

题意

定义一个数组的中位数为数组中第$\lceil \frac{n}{2}\rceil$个元素（下标从1开始）

给定一个排好序（递增）且长度为 $n\ast k$ 的数组，问你如何将其划分为$k$个长度为$n$的小数组，使这$k$个数组的中位数之和最大。输出最大的和。

思路

肯定是尽量取大的数作为每组的中位数，容易想到，每次后面取多少个，前面就配对多少个。要满足中位数为后面取的较大的数，即每次后面都取的比前面取的多。

即每次后面取$n/2+1$个，保证中位数为较大数。

代码

#include 

using namespace std;
typedef long long ll;
const int N = 2e5 + 10;
int a[N];

int main() {
    int T;
    cin >> T;
    while (T--) {
        int n, k;
        cin >> n >> k;
        for (int i = 1; i <= n * k; ++i) {
            cin >> a[i];
        }
        int st = 0, ed = n * k + 1;
        ll ans = 0;
        for (int i = 1; i <= k; ++i) {
            vector<int> vec;
            if (n % 2) {
                st += n / 2;
                ed -= n / 2 + 1;
            } else {
                st += n / 2 - 1;
                ed -= n / 2 + 1;
            }
            ans += a[ed];
        }
        cout << ans << '\n';
    }
    return 0;
}

C1 Binary Table (Easy Version)

题意

给定一个$n\ast m$的01矩阵，每次操作，你可以将矩阵中任意一个$2\ast 2$的格子中的$3$格取反（必须选3格）。

在$3\ast n\ast m$次操作内，将矩阵中每个1转为0。

思路

因为怕做不出C2，而且C1思路秒出，所以先写的C1。

一共可以做$3\ast n\ast m$次操作，容易想到每个格子可以分配到 3 次操作，即 3 次操作内将这个格子变为0而其它格子不变。

还是很简单的嘛。

代码

#include 

using namespace std;
typedef long long ll;
const int N = 1e2 + 10;
int a[N][N];

int main() {
    int T;
    cin >> T;
    while (T--) {
        int n, m;
        cin >> n >> m;
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= m; ++j) {
                scanf("%1d", &a[i][j]);
            }
        }
        int tot = 0;
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= m; ++j) {
                if (a[i][j]) tot += 3;
            }
        }
        cout << tot << '\n';
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= m; ++j) {
                if (a[i][j]) {
                    int fx = 1, fy = 1;
                    if (i == n) fx = -1;
                    if (j == m) fy = -1;
                    printf("%d %d %d %d %d %d\n", i, j, i + fx, j, i + fx, j + fy);
                    printf("%d %d %d %d %d %d\n", i, j, i, j + fy, i + fx, j);
                    printf("%d %d %d %d %d %d\n", i, j, i + fx, j + fy, i, j + fy);
                }
            }
        }
    }
    return 0;
}

C2 Binary Table (Hard Version)

题意

和C1同样题意，但操作次数只能是$n\ast m$以内

思路

可以全部分类讨论，大概300行，太麻烦不想写（逃

打的时候想了大概10min左右，其实想得到我这个思路模拟起来估计也就几十行代码量。但是当时脑子里全是黄金回旋，给自己搞了个回旋式的，代码量 *= 2。实际上根本不需要那么去弄，不然早十几分钟出该上紫了（

我是傻逼

言归正传，先考虑前$n-2$列，我们直接循环处理每一格。若该格目前为 1 ，则我们把它变为 0 ，另外两个操作随便操作两个它的后继格子（即尚未处理的格子）。

现在只剩两列没有处理了。先考虑前 $m-2$ 行，若该行已经是 0 0，则不需要操作。否则，把它变为 0 0 时，多出来的操作则给下面一行。

最后只剩一个 $2\ast 2$ 的矩阵，不管它是什么样的，我们都一定能 4 步内将其变为全0，过程，做了C1或者自己画一画肯定能出。

代码

//from toish
//我自己写的黄金回旋太鬼畜就不放出来了
#include 
using namespace std;
typedef pair<int, int> pii;
int tab[205][205];
vector<pii> vec;

void push(pii a, pii b, pii c) {
    vec.push_back(a); tab[a.first][a.second] ^= 1;
    vec.push_back(b); tab[b.first][b.second] ^= 1;
    vec.push_back(c); tab[c.first][c.second] ^= 1;
}


int dr[] = {0, 0, 1, 1};
int dc[] = {0, 1, 0, 1};
void fill22(int kr, int kc) {
    int cnt = 0;
    vector<pii> nod0, nod1;
    for (int d = 0; d < 4; ++d) {
        int r = kr + dr[d], c = kc + dc[d];
        if (tab[r][c]) cnt++, nod1.emplace_back(r, c);
        else nod0.emplace_back(r, c);
    }
    if (cnt == 1) {
        push(nod1[0], nod0[0], nod0[1]);
        push(nod1[0], nod0[1], nod0[2]);
        push(nod1[0], nod0[0], nod0[2]);
    } else if (cnt == 2) {
        push(nod1[1], nod0[0], nod0[1]);
        push(nod1[0], nod0[0], nod0[1]);
    } else if (cnt == 3) {
        push(nod1[0], nod1[1], nod1[2]);
    } else if (cnt == 4) {
        push(nod1[1], nod1[2], nod1[3]);
        push(nod1[0], nod1[1], nod1[2]);
        push(nod1[0], nod1[1], nod1[3]);
        push(nod1[0], nod1[2], nod1[3]);
    }
}

int main() {
    int T;  scanf("%d", &T);
    while (T--) {
        vec.clear();
        int n, m;   scanf("%d%d", &n, &m);
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= m; ++j) scanf("%1d", &tab[i][j]);
        }
        for (int c = 1; c <= m-2; ++c) {
            for (int r = 1; r <= n-1; ++r) {
                if (tab[r][c]) push({r, c}, {r, c+1}, {r+1, c+1});
            }
            if (tab[n][c]) push({n, c}, {n, c+1}, {n-1, c+1});
        }
        for (int r = 1; r <= n-2; ++r) {
            for (int c = m-1; c <= m; ++c) {
                if (tab[r][c] && tab[r][c+1]) push({r, c}, {r, c+1}, {r+1, c});
                else if (tab[r][c]) push({r, c}, {r+1, c}, {r+1, c+1});
                else if (tab[r][c+1]) push({r, c+1}, {r+1, c}, {r+1, c+1});
            }
        }
        fill22(n-1, m-1);
        printf("%lu\n", vec.size()/3);
        for (int i = 0; i < vec.size(); ++i) {
            printf("%d %d%c", vec[i].first, vec[i].second, " \n"[(i+1)%3 == 0]);
        }
    }
}

(然而本菜鸡这辈子还没上过紫，我是fw)

有机会一定补后两题（gugugu