CSS的动画和交互-贝塞尔曲线

说明

每天10分钟，重构你的前端知识体系专栏笔记。

一、介绍

这一节学习一下 CSS的动画和交互。

二、animation 属性

2.1、基本用法

@keyframes mykf
{
  from {background: red;}
  to {background: yellow;}
}

div
{
    animation: mykf 5s infinite;
}

2.2、六个部分

animation-name 动画的名称，是一个 keyframes 类型的值
animation-duration 动画的时长
animation-timing-function 动画的时间曲线
animation-delay 动画开始前的延迟
animation-iteration-count 动画的播放次数
animation-direction 动画的方向

三、transition 属性

3.1、四个部分

transition-property 要变换的属性
transition-duration 变换的时长
transition-timing-function 时间曲线
transition-delay 延迟

3.2、组合

/* 定义transition达到各段曲线都不同的效果 */
@keyframes mykf {
  from { top: 0; transition:top ease}
  50% { top: 30px;transition:top ease-in }
  75% { top: 10px;transition:top ease-out }
  to { top: 0; transition:top linear}
}

四、三次贝塞尔曲线

贝塞尔曲线是一种插值曲线，它描述了两个点之间差值来形成连续的曲线形状的规则。

K 次贝塞尔插值算法需要 k+1 个控制点，最简单的一次贝塞尔插值就是线性插值，将时间表示为 0 到 1 的区间;

4.1、一次贝塞尔插值公式

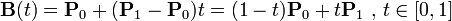
4.2、二次贝塞尔插值公式

4.3、三次贝塞尔插值公式

4.4、JavaScript版本的代码

翻译自webkit的C++代码，这个JavaScript版本的三次贝塞尔曲线可以用于实现跟CSS一模一样的动画

// 浏览器一般采用了数值算法
function generate(p1x, p1y, p2x, p2y) {
    const ZERO_LIMIT = 1e-6;
    // Calculate the polynomial coefficients,
    // implicit first and last control points are (0,0) and (1,1).
    const ax = 3 * p1x - 3 * p2x + 1;
    const bx = 3 * p2x - 6 * p1x;
    const cx = 3 * p1x;

    const ay = 3 * p1y - 3 * p2y + 1;
    const by = 3 * p2y - 6 * p1y;
    const cy = 3 * p1y;

    function sampleCurveDerivativeX(t) {
        // `ax t^3 + bx t^2 + cx t' expanded using Horner 's rule.
        return (3 * ax * t + 2 * bx) * t + cx;
    }

    function sampleCurveX(t) {
        return ((ax * t + bx) * t + cx ) * t;
    }

    function sampleCurveY(t) {
        return ((ay * t + by) * t + cy ) * t;
    }

    // Given an x value, find a parametric value it came from.
    function solveCurveX(x) {
        var t2 = x;
        var derivative;
        var x2;

        // https://trac.webkit.org/browser/trunk/Source/WebCore/platform/animation
        // First try a few iterations of Newton's method -- normally very fast.
        // http://en.wikipedia.org/wiki/Newton's_method
        for (let i = 0; i < 8; i++) {
            // f(t)-x=0
            x2 = sampleCurveX(t2) - x;
            if (Math.abs(x2) < ZERO_LIMIT) {
                return t2;
            }
            derivative = sampleCurveDerivativeX(t2);
            // == 0, failure
            /* istanbul ignore if */
            if (Math.abs(derivative) < ZERO_LIMIT) {
                break;
            }
            t2 -= x2 / derivative;
        }

        // Fall back to the bisection method for reliability.
        // bisection
        // http://en.wikipedia.org/wiki/Bisection_method
        var t1 = 1;
        /* istanbul ignore next */
        var t0 = 0;

        /* istanbul ignore next */
        t2 = x;
        /* istanbul ignore next */
        while (t1 > t0) {
            x2 = sampleCurveX(t2) - x;
            if (Math.abs(x2) < ZERO_LIMIT) {
                return t2;
            }
            if (x2 > 0) {
                t1 = t2;
            } else {
                t0 = t2;
            }
            t2 = (t1 + t0) / 2;
        }

        // Failure
        return t2;
    }

    function solve(x) {
        return sampleCurveY(solveCurveX(x));
    }

    return solve;
}

五、贝塞尔曲线拟合

5.1、用于模拟抛物线

  
  
  
  


   运动时间：s

   初速度： px/s

   水平速度： px/s

   重力： px/s²

   来一个球 

// 核心函数
function generateCubicBezier (v, g, t){
    var a = v / g;
    var b = t + v / g;

    return [[(a / 3 + (a + b) / 3 - a) / (b - a), (a * a / 3 + a * b * 2 / 3 - a * a) / (b * b - a * a)],
        [(b / 3 + (a + b) / 3 - a) / (b - a), (b * b / 3 + a * b * 2 / 3 - a * a) / (b * b - a * a)]];
}

function createBall() {
  var ball = document.createElement("div");
  var t = Number(document.getElementById("t").value);
  var vx = Number(document.getElementById("vx").value);
  var vy = Number(document.getElementById("vy").value);
  var g = Number(document.getElementById("g").value);
  ball.className = "ball";
  document.body.appendChild(ball)
  ball.style.transition = `left linear ${t}s, top cubic-bezier(${generateCubicBezier(vy, g, t)}) ${t}s`;
  setTimeout(function(){
    ball.style.left = `${vx * t}px`; 
    ball.style.top = `${vy * t + 0.5 * g * t * t}px`; 
  }, 100);
  setTimeout(function(){ document.body.removeChild(ball); }, t * 1000);
}

转载于：https://blog.csdn.net/kaimo313/article/details/95101468