《动手学——梯度下降》笔记

梯度下降

一维梯度下降

证明：沿梯度反方向移动自变量可以减小函数值

泰勒展开：

$$f(x+ϵ)=f(x)+ϵf^{\prime }(x)+\mathcal{O}\left({ϵ}^2\right)$$

代入沿梯度方向的移动量 $\eta f^{\prime }(x)$：

$$f\left(x-\eta f^{\prime }(x)\right)=f(x)-\eta f^{\prime 2}(x)+\mathcal{O}\left({\eta }^2{f}^{\prime 2}(x)\right)$$

$$f\left(x-\eta f^{\prime }(x)\right)\lesssim f(x)$$

$$x\leftarrow x-\eta f^{\prime }(x)$$

★ 将x沿梯度反方向移动η倍的步长

学习率η

学习率如果过小，会导致梯度下降每次迭代时的函数值下降的幅度很小，收敛速度很慢，需要多次迭代。
如果过大，会导致梯度增加，反而出现了发散的情况

show_trace(gd(0.05))
#初始化是10

show_trace(gd(1.1))
#初始化是10

局部极小值

#初始值10，学习率2，迭代后到达局部最小值。————原因学习率过大导致

多维梯度下降

梯度不再是一个标量，而是对各个自变量求偏导之后的向量。

$$\nabla f(\mathbf{x})={\left[\frac{\partial f(\mathbf{x})}{\partial x_1},\frac{\partial f(\mathbf{x})}{\partial x_2},\dots ,\frac{\partial f(\mathbf{x})}{\partial x_d}\right]}^{\top }$$

$$f(\mathbf{x}+ϵ)=f(\mathbf{x})+{ϵ}^{\top }\nabla f(\mathbf{x})+\mathcal{O}\left(\Vert ϵ{\Vert }^2\right)$$

$$\mathbf{x}\leftarrow \mathbf{x}-\eta \nabla f(\mathbf{x})$$

★ 也是将x沿梯度反方向移动η倍的步长

def train_2d(trainer, steps=20):  #trainer指参数x1和x2如何更新，steps指迭代次数
    x1, x2 = -5, -2
    results = [(x1, x2)]  #赋初值
    for i in range(steps):
        x1, x2 = trainer(x1, x2)  #迭代
        results.append((x1, x2))  #参数更新
    print('epoch %d, x1 %f, x2 %f' % (i + 1, x1, x2))
    return results

def show_trace_2d(f, results): 
    d2l.plt.plot(*zip(*results), '-o', color='#ff7f0e')
    x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1))
    d2l.plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')  #等高线
    d2l.plt.xlabel('x1')
    d2l.plt.ylabel('x2')

eta = 0.1

def f_2d(x1, x2):  # 目标函数
    return x1 ** 2 + 2 * x2 ** 2

def gd_2d(x1, x2):  # 更新方法
    return (x1 - eta * 2 * x1, x2 - eta * 4 * x2)

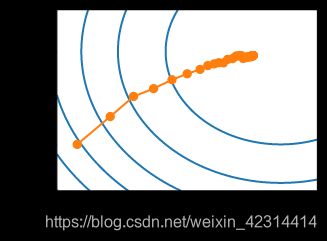
show_trace_2d(f_2d, train_2d(gd_2d))

# 多维梯度下降的直观理解：圆圈是等高线，表示x1=x2
# 梯度下降呈现垂直于等高线的方向收敛，最后收敛到极小值点

自适应方法

选择学习率（过小/过小？）————寻找方法自动调节学习率/不需要学习率

牛顿法

典型的考虑到二阶导数的方法
在 $x+ϵ$ 处泰勒展开：

$$f(\mathbf{x}+ϵ)=f(\mathbf{x})+{ϵ}^{\top }\nabla f(\mathbf{x})+\frac{1}{2}{ϵ}^{\top }\nabla {\nabla }^{\top }f(\mathbf{x})ϵ+\mathcal{O}\left(\Vert ϵ{\Vert }^3\right)$$

最小值点处满足: $\nabla f(\mathbf{x})=0$, 即我们希望 $\nabla f(\mathbf{x}+ϵ)=0$, 对上式关于 $ϵ$ 求导，忽略高阶无穷小，有：

$$\nabla f(\mathbf{x})+{\mathbf{H}}_f\mathbf{ϵ}=0\text{ and hence }ϵ=-{\mathbf{H}}_f^{-1}\nabla f(\mathbf{x})$$

c = 0.5

def f(x):
    return np.cosh(c * x)  # Objective

def gradf(x):
    return c * np.sinh(c * x)  # Derivative

def hessf(x):
    return c**2 * np.cosh(c * x)  # Hessian 二阶导数

# Hide learning rate for now
def newton(eta=1):
    x = 10
    results = [x]
    for i in range(10):
        x -= eta * gradf(x) / hessf(x)  #牛顿法更新公式————x减η倍的一阶导数/二阶导数
        results.append(x)
    print('epoch 10, x:', x)
    return results

show_trace(newton())

c = 0.15 * np.pi

def f(x):
    return x * np.cos(c * x)

def gradf(x):
    return np.cos(c * x) - c * x * np.sin(c * x)

def hessf(x):
    return - 2 * c * np.sin(c * x) - x * c**2 * np.cos(c * x)

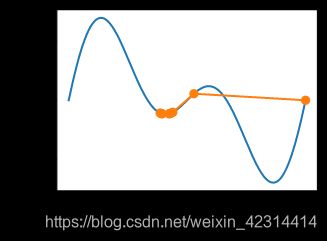
show_trace(newton())

show_trace(newton(0.5))

#对于有局部最小值的情况下，和梯度下降方法有同样的问题，还是需要调节学习率

牛顿法收敛性分析

只考虑在函数为凸函数, 且最小值点上 $f^{\prime \prime }(x^{\ast })>0$ 时的收敛速度：

令 $x_k$ 为第 $k$ 次迭代后 $x$ 的值， $e_k:=x_k-x^{\ast }$ 表示 $x_k$ 到最小值点 $x^{\ast }$ 的距离，由 $f^{\prime }(x^{\ast })=0$:

$$0=f^{\prime }\left(x_k-e_k\right)=f^{\prime }\left(x_k\right)-e_k{f}^{\prime \prime }\left(x_k\right)+\frac{1}{2}{e}_k^2{f}^{\prime \prime \prime }\left({\xi }_k\right)\text{for some }{\xi }_k\in \left[x_k-e_k,x_k\right]$$

两边除以 $f^{\prime \prime }(x_k)$, 有：

$$e_k-f^{\prime }\left(x_k\right)/f^{\prime \prime }\left(x_k\right)=\frac{1}{2}{e}_k^2{f}^{\prime \prime \prime }\left({\xi }_k\right)/f^{\prime \prime }\left(x_k\right)$$

代入更新方程 $x_{k+1}=x_k-f^{\prime }\left(x_k\right)/f^{\prime \prime }\left(x_k\right)$, 得到：

$$x_k-x^{\ast }-f^{\prime }\left(x_k\right)/f^{\prime \prime }\left(x_k\right)=\frac{1}{2}{e}_k^2{f}^{\prime \prime \prime }\left({\xi }_k\right)/f^{\prime \prime }\left(x_k\right)$$

$$x_{k+1}-x^{\ast }=e_{k+1}=\frac{1}{2}{e}_k^2{f}^{\prime \prime \prime }\left({\xi }_k\right)/f^{\prime \prime }\left(x_k\right)$$

当 $\frac{1}{2}{f}^{\prime \prime \prime }\left({\xi }_k\right)/f^{\prime \prime }\left(x_k\right)\le c$ 时，有:

$$e_{k+1}\le c{e}_k^2$$

随机梯度下降

随机梯度下降参数更新

对于有 $n$ 个样本对训练数据集，设 $f_i(x)$ 是第 $i$ 个样本的损失函数, 则目标函数为:

$$f(\mathbf{x})=\frac{1}{n}\sum _{i=1}^n{f}_i(\mathbf{x})$$

其梯度为:

$$\nabla f(\mathbf{x})=\frac{1}{n}\sum _{i=1}^n\nabla f_i(\mathbf{x})$$

使用该梯度的一次更新的时间复杂度为 $\mathcal{O}(n)$

随机梯度下降更新公式 $\mathcal{O}(1)$:

$$\mathbf{x}\leftarrow \mathbf{x}-\eta \nabla f_i(\mathbf{x})$$
（每一个样本计算完梯度后，都对参数进行更新，这样的话时间复杂度就降到了O1）

且有：

$${\mathbb{E}}_i\nabla f_i(\mathbf{x})=\frac{1}{n}\sum _{i=1}^n\nabla f_i(\mathbf{x})=\nabla f(\mathbf{x})$$

def f(x1, x2):
    return x1 ** 2 + 2 * x2 ** 2  # Objective

def gradf(x1, x2):
    return (2 * x1, 4 * x2)  # Gradient

def sgd(x1, x2):  # Simulate noisy gradient
    global lr  # Learning rate scheduler
    (g1, g2) = gradf(x1, x2)  # Compute gradient
    (g1, g2) = (g1 + np.random.normal(0.1), g2 + np.random.normal(0.1))
    eta_t = eta * lr()  # Learning rate at time t
    return (x1 - eta_t * g1, x2 - eta_t * g2)  # Update variables

eta = 0.1
lr = (lambda: 1)  # Constant learning rate  学习率 1
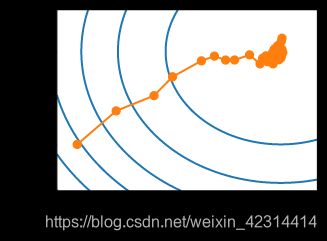
show_trace_2d(f, train_2d(sgd, steps=50))

#下图：最优点附近一直进行抖动，每一次参数更新，都会梯度更新。
#思考：可以一开始使用较小学习速率，然后较大，最后再使用较小的。

动态学习率

解决上述问题
三种规划学习率的函数：不同时间段赋值；指数；多项式

$$\begin{array}{ll}\eta (t)={\eta }_i\text{ if }{t}_i\le t\le t_{i+1}& \text{ piecewise constant }\\ \eta (t)={\eta }_0\cdot e^{-\lambda t}& \text{ exponential }\\ \eta (t)={\eta }_0\cdot (\beta t+1{)}^{-\alpha }& \text{ polynomial }\end{array}$$

#指数 结果有了明显改善

def exponential():
    global ctr
    ctr += 1  #ctr迭代次数
    return math.exp(-0.1 * ctr)

ctr = 1
lr = exponential  # Set up learning rate
show_trace_2d(f, train_2d(sgd, steps=1000))

#多项式  结果有了明显改善
def polynomial():
    global ctr
    ctr += 1
    return (1 + 0.1 * ctr)**(-0.5)

ctr = 1
lr = polynomial  # Set up learning rate
show_trace_2d(f, train_2d(sgd, steps=50))

小批量随机梯度下降

认为梯度下降和随机梯度下降是走了两个极端，各有优劣。

梯度下降，每次参数更新使用的是整个数据集上所有样本的平均梯度来更新参数。对于有一定的相似性一定的共性的数据利用率较低。

随机梯度下降，每次参数更新时使用的是单个样本的梯度。没有充分利用cpu/gpu具有的矢量计算和多线程的能力。

二者的折中选项：小批量随机梯度下降，每次参数更新使用的是一部分的样本，对这些样本梯度取均值然后进行参数更新。

读取数据

def get_data_ch7():  # 本函数已保存在d2lzh_pytorch包中方便以后使用
    data = np.genfromtxt('/home/kesci/input/airfoil4755/airfoil_self_noise.dat', delimiter='\t')
    data = (data - data.mean(axis=0)) / data.std(axis=0) # 标准化（减均值除方差）
    return torch.tensor(data[:1500, :-1], dtype=torch.float32), \
           torch.tensor(data[:1500, -1], dtype=torch.float32) # 前1500个样本(每个样本5个特征)
           #最后一列用作label，其余的用作feature

features, labels = get_data_ch7()
features.shape

import pandas as pd
df = pd.read_csv('/home/kesci/input/airfoil4755/airfoil_self_noise.dat', delimiter='\t', header=None)
df.head(10)

从零开始实现

def sgd(params, states, hyperparams):  #params模型的参数，hyperparams学习率lr
    for p in params: #对于每一个参数
        p.data -= hyperparams['lr'] * p.grad.data  #梯度下降

# 本函数已保存在d2lzh_pytorch包中方便以后使用
def train_ch7(optimizer_fn, states, hyperparams, features, labels,
              batch_size=10, num_epochs=2): 
             #optimizer_fn参数如何更新（即sgd），batch_size每个batch样本数量，num_epochs整个训练集训练几次
    # 初始化模型
    net, loss = d2l.linreg, d2l.squared_loss   #线性回归模型；均方误差损失函数
    
    w = torch.nn.Parameter(torch.tensor(np.random.normal(0, 0.01, size=(features.shape[1], 1)), dtype=torch.float32),
                           requires_grad=True)
    b = torch.nn.Parameter(torch.zeros(1, dtype=torch.float32), requires_grad=True)

    def eval_loss():  #损失函数
        return loss(net(features, w, b), labels).mean().item()

    ls = [eval_loss()]
    data_iter = torch.utils.data.DataLoader(   #数据迭代器，每次训练返回一个batch，大小是batch_size
        torch.utils.data.TensorDataset(features, labels), batch_size, shuffle=True)
    
    #训练
    for _ in range(num_epochs):
        start = time.time()
        for batch_i, (X, y) in enumerate(data_iter):  #batch_i第几次数据，迭代次数
            l = loss(net(X, w, b), y).mean()  # 使用平均损失
            
            # 梯度清零
            if w.grad is not None:
                w.grad.data.zero_()
                b.grad.data.zero_()
                
            l.backward()  #反向传播/设置梯度的过程
            optimizer_fn([w, b], states, hyperparams)  # 迭代模型参数
            if (batch_i + 1) * batch_size % 100 == 0:   #第十个batch，就是用了一百个样本
                ls.append(eval_loss())  # 每100个样本记录下当前训练误差
    # 打印结果和作图
    print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
    d2l.set_figsize()
    d2l.plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
    d2l.plt.xlabel('epoch')
    d2l.plt.ylabel('loss')

def train_sgd(lr, batch_size, num_epochs=2):
    train_ch7(sgd, None, {'lr': lr}, features, labels, batch_size, num_epochs)

对比

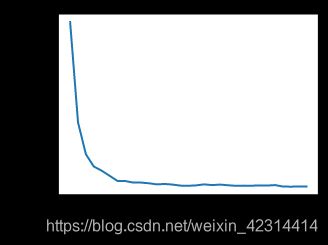
train_sgd(1, 1500, 6)  #梯度下降，学习率为1，batch_size即数据集大小1500，用了所有的样本做梯度更新

#用了6个epoch，每个0.009881秒

train_sgd(0.005, 1)  #对应随机梯度下降，每次只用一个样本做梯度更新

#用了2个epoch，每个0.463836秒

train_sgd(0.05, 10)  #小批量随机梯度下降

#用了2个epoch，每个0.065017秒

简洁实现

# 本函数与原书不同的是这里第一个参数优化器函数而不是优化器的名字
# 例如: optimizer_fn=torch.optim.SGD, optimizer_hyperparams={"lr": 0.05}
def train_pytorch_ch7(optimizer_fn, optimizer_hyperparams, features, labels,
                    batch_size=10, num_epochs=2):
    # 初始化模型
    net = nn.Sequential(
        nn.Linear(features.shape[-1], 1)
    )
    loss = nn.MSELoss()
    optimizer = optimizer_fn(net.parameters(), **optimizer_hyperparams)

    def eval_loss():
        return loss(net(features).view(-1), labels).item() / 2

    ls = [eval_loss()]
    data_iter = torch.utils.data.DataLoader(
        torch.utils.data.TensorDataset(features, labels), batch_size, shuffle=True)

    for _ in range(num_epochs):
        start = time.time()
        for batch_i, (X, y) in enumerate(data_iter):
            # 除以2是为了和train_ch7保持一致, 因为squared_loss中除了2
            l = loss(net(X).view(-1), y) / 2 
            
            optimizer.zero_grad()
            l.backward()
            optimizer.step()
            if (batch_i + 1) * batch_size % 100 == 0:
                ls.append(eval_loss())
    # 打印结果和作图
    print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
    d2l.set_figsize()
    d2l.plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
    d2l.plt.xlabel('epoch')
    d2l.plt.ylabel('loss')

train_pytorch_ch7(optim.SGD, {"lr": 0.05}, features, labels, 10)
#小批量梯度下降

习题

1. 关于梯度下降描述正确的是：_______。 d

   梯度下降是沿梯度方向移动自变量从而减小函数值。

   梯度下降学习率越大下降得越快，所以学习率越大越好。

   梯度下降学习率越大越容易发散，所以学习率越小越好。

   局部极小值是梯度下降算法面临的一个挑战。

   答案解释 选项1: 错误，梯度下降是沿着梯度的反方向移动自变量从而减小函数值的。

   关于牛顿法说法错误的是：______。 c

   牛顿法相比梯度下降的一个优势在于：梯度下降“步幅”的确定比较困难，而牛顿法相当于可以通过Hessian矩阵来调整“步幅”。

   牛顿法需要计算Hessian矩阵的逆，计算量比较大。

   相比梯度下降法，牛顿法可以避免局部极小值的问题。

   在牛顿法中，局部极小值也可以通过调整学习率来解决。

   随机梯度下降的时间复杂度是_____。 a

   O(1)

   O(n)

   O(logn)

   O(n 2 )

   关于动态学习率的说法，错误是_______。 d

   在最开始学习率设计比较大，加速收敛

   学习率可以设计为指数衰减或多项式衰减

   在优化进行一段时间后可以适当减小学习率来避免振荡

   动态学习率可以随着迭代次数增加而增大学习率

   答案解释 选项4错误，应该随着迭代次数增加减小学习率。

   可以通过修改视频中 train_sgd 函数的参数_______来分别使用梯度下降、随机梯度下降和小批量随机梯度下降。 a

   batch_size

   lr

   num_epochs

   都不可以

   答案解释 选项1正确，三者的区别在于每次更新时用的样本量。