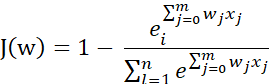3种softmax函数python实现方式（显式循环，向量，矩阵）

Python三种方式实现Softmax损失函数计算

python实现的softmax损失函数代码，我们先回顾一下softmax损失函数的定义：

其中右边一项为第y=j项的概率值。令J(w) = log(J(w)):

损失函数的梯度：

 

import numpy as np
"""
    第一种计算softmax_loss, 在计算每一分类的概率时，用到了矩阵运算。
"""
class Softmax:

    def __init__(self):
        pass

    @staticmethod
    def softmax_loss_naive(w, x, y, reg):
        """
        使用显示循环版本计算softmax损失函数
        N:数据个数， D：数据维度， C:数据类别个数
        inputs:
        :param w: shape:[D, C], 分类器权重参数
        :param x: shape:[N, D] 训练数据
        :param y: shape:[N, ]数据标记
        :param reg: 惩罚项系数
        :return:二元组：loss:数据损失值， dw：权重w对应的梯度，其形状和w相同
        """
        loss = 0.0
        dw = np.zeros_like(w)
        #############################################################################
        #  任务：使用显式循环实现softmax损失值loss及相应的梯度dW 。                    #
        #  温馨提示： 如果不慎,将很容易造成数值上溢。别忘了正则化哟。                   #
        #############################################################################
        y = np.asarray(y, dtype=np.int)
        num_train, dim = x.shape
        num_class = w.shape[1]
        score = x.dot(w)
        score_max = np.max(score, axis=1).reshape(num_train, 1)
        # 计算对数概率， prob.shape = N*D, 每一行与一个样本对应， 每一行的概率和为1
        z = np.sum(np.exp(score - score_max), axis=1, keepdims=True)
        z1 = np.sum(np.exp(score - score_max), axis=1)
        e_j =  np.exp(score - score_max)
        prob = e_j / z
        for i in range(num_train):
            loss += -np.log(prob[i, y[i, 0]]) # loss = 1 - prob[i, y[i, 0]], loss = log(loss), so loss = -np.log(prob[i, y[i]])
            for j in range(num_class):
                if j == y[i]:
                    dw[:, j] += -(1-prob[i, j]) * x[i]
                else:
                    dw[:, j] += prob[i, j] * x[i]
        loss = loss / num_train + 0.5 * reg * np.sum(w*w)
        dw = dw / num_train + reg * w
        return loss, dw

    """
        第二种计算softmax_loss, 纯向量计算
    """
    @staticmethod
    def softmax_loss_naive_vec(w, x, y, reg):
        """
           N:数据个数， D：数据维度， C:数据类别个数
           inputs:
           :param w: shape:[D, C], 分类器权重参数
           :param x: shape:[N, D] 训练数据
           :param y: shape:[N, ]数据标记
           :param reg: 惩罚项系数
           :return:二元组：loss:数据损失值， dw：权重w对应的梯度，其形状和w相同
           """
        loss = 0.0
        dw = np.zeros_like(w)
        #############################################################################
        #  任务：使用显式循环实现softmax损失值loss及相应的梯度dW 。                    #
        #  温馨提示： 如果不慎,将很容易造成数值上溢。别忘了正则化哟。                   #
        #############################################################################
        num_train = x.shape[0]
        num_class = w.shape[1]
        y = np.asarray(y, dtype=np.int)
        for i in range(num_train):
            s = x[i].dot(w)
            score = s - np.max(s)
            score_E = np.exp(score)
            Z = np.sum(score_E)
            score_target = score_E[y[i]]
            loss += -np.log(score_target / Z)
            for j in range(num_class):
                if j == y[i]:
                    dw[:, j] += -x[i] * (1 - score_E[j] / Z)
                else:
                    dw[:, j] += x[i] * (score_E[j] / Z)

        loss = loss / num_train + 0.5*reg*np.sum(w*w)
        dw = dw / num_train + reg*w
        return loss, dw

    """
        纯矩阵计算
    """
    @staticmethod
    def softmax_loss_matrix(w, x, y, reg):
        """
               使用纯矩阵运算
               N:数据个数， D：数据维度， C:数据类别个数
               inputs:
               :param w: shape:[D, C], 分类器权重参数
               :param x: shape:[N, D] 训练数据
               :param y: shape:[N, ]数据标记
               :param reg: 惩罚项系数
               :return:二元组：loss:数据损失值， dw：权重w对应的梯度，其形状和w相同
               """
        loss = 0.0
        dw = np.zeros_like(w)
        #############################################################################
        #  任务：使用显式循环实现softmax损失值loss及相应的梯度dW 。                    #
        #  温馨提示： 如果不慎,将很容易造成数值上溢。别忘了正则化哟。                   #
        #############################################################################
        num_train = x.shape[0]
        y = np.asarray(y, dtype=np.int)
        s = x.dot(w)
        score = s - np.max(s, axis=1, keepdims=True)
        score_E = np.exp(score)
        Z = np.sum(score_E, axis=1, keepdims=True)
        prob = score_E / Z
        y_true_class = np.zeros_like(prob)
        y_true_class[range(num_train), y.reshape(num_train)] = 1.0
        loss += -np.sum(y_true_class * np.log(prob)) / num_train + 0.5*reg*np.sum(w*w)
        dw += -np.dot(x.T,y_true_class - prob) / num_train + reg * w
        return loss, dw