Leetcode循环队列
这道题十分考验我们对队列的理解。
文章目录
-
-
- 队列的介绍
- 队列的实现
- 进入正题
-
队列的介绍
队列是一种只允许在一段进行插入,在另一端进行删除的数据操作的特殊线性结构,,因此决定了他具有先入先出的特点,其中进行插入操作的一段叫做队尾,出队列的一端叫做队头。
队列的实现
队列可以使用链表或者数组进行实现,对于这两种实现方法,使用链表实现效果更好一点,两个指针中front为链表的头,即队列的队头,出数据的话只需要找到front的下一个假设为pre,将front销毁,front置为pre即可,如果是用数组的结构的话,出队列在数组头上出数据,效率会很低。
链表实现队列代码如下
Queue.h
#pragma once
#include Queue.c
#define _CRT_SECURE_NO_WARNINGS
#include "Queueh.h"
void QueueInit(Que* pq)
{
assert(pq);
pq->head = pq->tail = NULL;
pq->size = 0;
}
void QueueDestroy(Que* pq)
{
assert(pq);
QNode* cur = pq->head;
while (cur != NULL)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
pq->head = pq->tail = NULL;
pq->size = 0;
}
void QueuePush(Que* pq, QDataType x)
{
assert(pq);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
newnode->next = NULL;
if (newnode == NULL)
{
perror("malloc fail");
exit(-1);
}
newnode->data = x;
if (pq->tail == NULL)//这里要先进行判断
{
pq->head = pq->tail = newnode;//如果队列里没有一个元素
//那么head和tail都为空,将newnode设置为队头,当然也是队尾,毕竟只有一个元素。
}
else
{
pq->tail->next = newnode;
pq->tail = newnode;
}
pq->size++;
}
void QueuePop(Que* pq)
{
assert(pq);
assert(!QueueEmpty(pq));//判空,避免引起不必要的错误。
if (pq->head->next != NULL)
{
QNode* next = pq->head->next;
free(pq->head);
pq->head = next;
}
else
{
free(pq->head);
pq->head = pq->tail = NULL;
}
pq->size--;
}
QDataType QueueFront(Que* pq)
{
assert(pq);
//判断是否为空
assert(!QueueEmpty(pq));
return pq->head->data;//队头位置
}
QDataType QueueBack(Que* pq)
{
assert(pq);
//判断是否为空
assert(!QueueEmpty(pq));
return pq->tail->data;//队尾位置
}
bool QueueEmpty(Que* pq)//判断是否为空,为空则返回true
{
if (pq->head == NULL)
{
return true;
}
else
{
return false;
}
}
int QueueSize(Que* pq)
{
assert(pq);
return pq->size;
}
进入正题
前边的队列如果空间不够就会扩容,但是这里的循环队列大小是固定的,只可以保存k个元素,当然还是遵循先入先出的规则。
例如下边的环形队列,在pop掉队头数据后,这块空间不会被销毁的,可以继续存储值覆盖原来的值,假设k等于5,当入6个元素后,这个循环队列就满了,当出队列时,此时这个队列的首位置就可以继续存储数据。
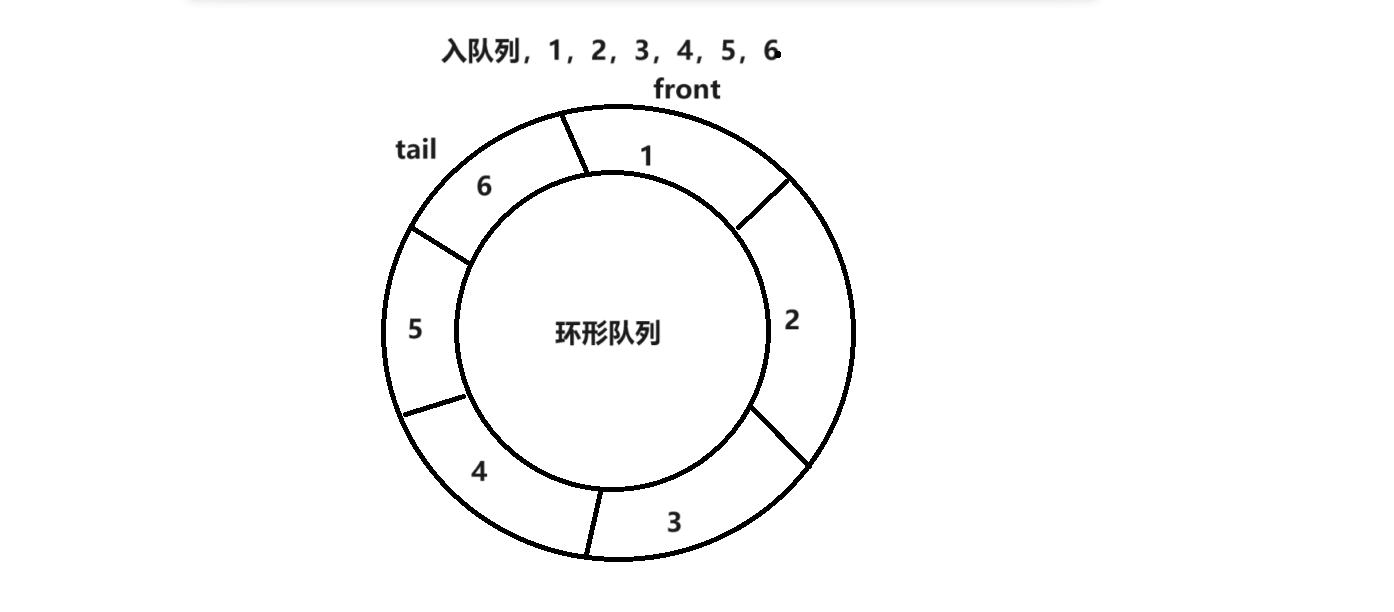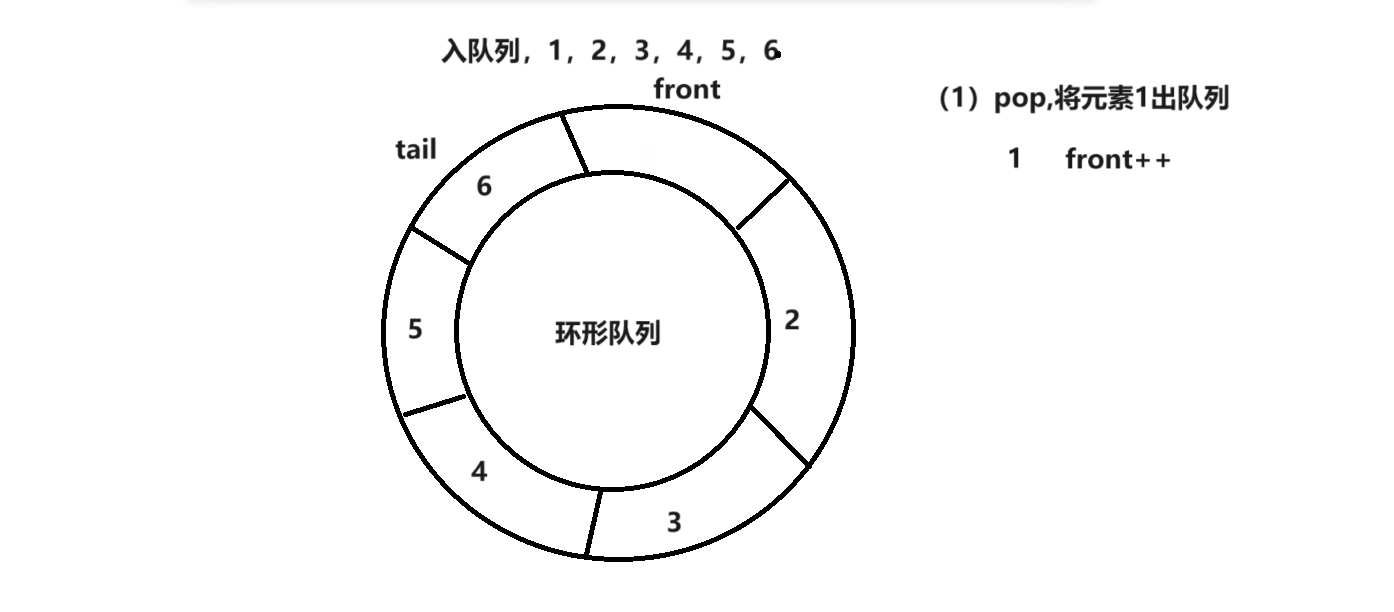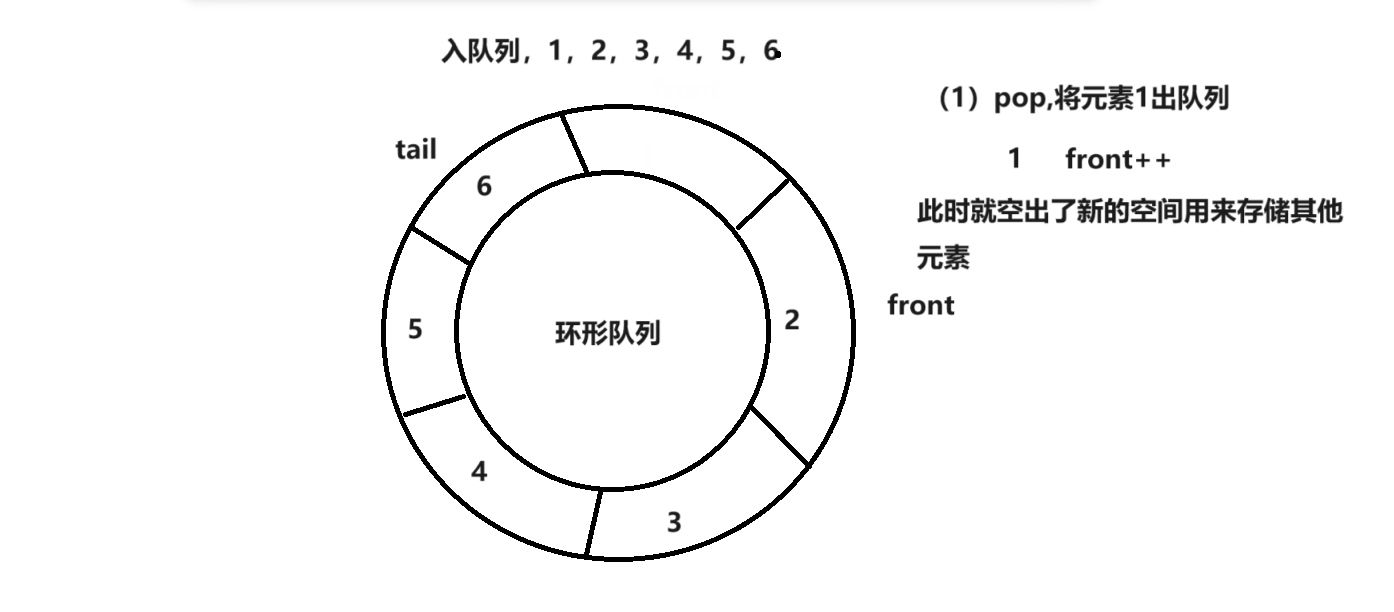
循环队列的思路和环形队列一样
那么这道题用数组实现比较好还是链表实现比较好呢?
我想你一定第一反应是用链表实现比较好,然而这道题相对于数组,链表实现就显得更加复杂一点
因为这也是一个环状结构,刚好可以实现一个环形链表来实现,但是我们要注意的是,链表的两个指针的状态通常是左闭右开。
即 [front,tail)
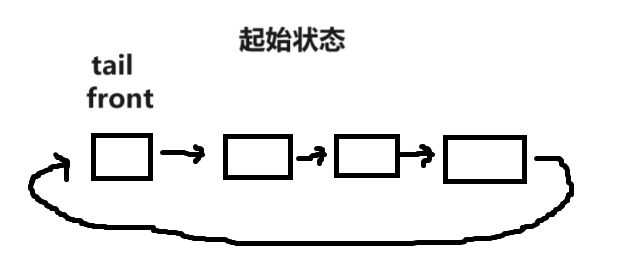
再插入一个数据后,tail=tail->next。
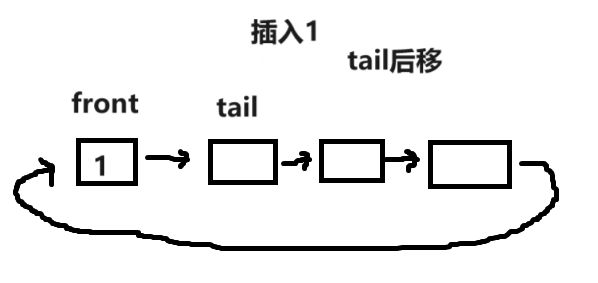
可以发现,tail总是在有效数字的下一位置。
和实现链表不同的地方是,链表的尾只有在开好后才会让tail指向尾节点,这里的链表长度是固定的,当一个元素入队列后,tail会指向下一个位置,如果是这样的话如何表示空和满呢?
当最后插入一个数据后,tail指向下一个位置刚好是front,判断为满?但是当队列里没有元素的话,tail和front的位置也是相同的,当然,如果你定义一个size来判断当然可以。
然而还有一个更大的缺陷就是题目要求获取队尾元素,如果是单向链表的话,想要找放到tail的前一个结点还需要遍历一边才行,如果用双向链表的话也可以,但是就有点太大费周章了。
如果用数组来实现会简单许多滴!
结构体声明如下
typedef struct {
int* a;
int front;
int rear;//尾
int k;
} MyCircularQueue;
初始化函数如下
MyCircularQueue* myCircularQueueCreate(int k) {
MyCircularQueue*obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
//多开一个方便区分空和满
obj->a=(int*)malloc(sizeof(int)*(k+1));
obj->k=k;
obj->front=obj->rear=0;
return obj;
}
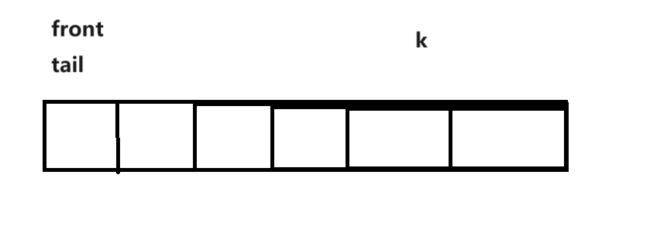
数组也面临一个同样的问题,如何判断是满还是空?
可以多开一块空间。k==5,开6块空间,最后一块空间浪费不用。
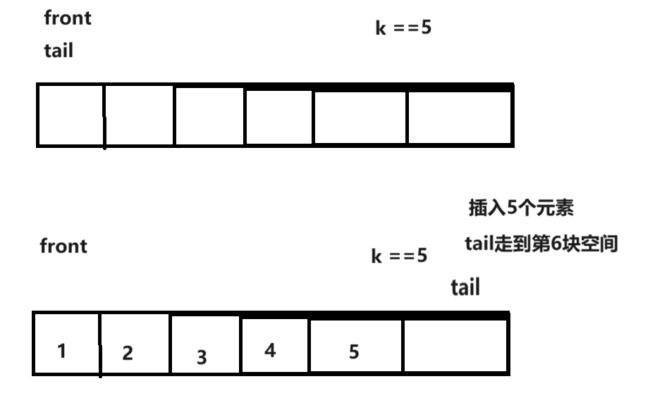
如果front等于tail就为空,在这里设置tail的值为0~5(要注意下标和位置有减一的关系),如果tail的下一个位置为front时,表示队列已满。
obj->tail%=(obj->k+1);//obj为循环队列变量
控制tail的值的变化范围,当tail等于6时置tail为0。
当然,在出队列过程中,front是会不断变化的。
我们看front变化的情况
pop一个数据后,向后移一位
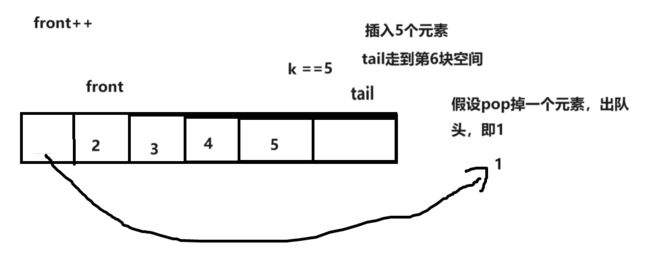
判断是否队列已满的条件判断句如下
(obj->tail+1)%(obj->k+1 )==obj->front
前边已经说过了,tail的变化范围为0~5,此时tail被置为0,但front为1,不相等,就表示还有空余的位置,队列没有满,所以上边的判断语句在任何场景都是正常使用的。
判断是否已满函数如下(题目中tail被rear替换)
bool myCircularQueueIsFull(MyCircularQueue* obj) {
return (obj->rear+1)%(obj->k+1 )==obj->front;
}
返回类型为布尔值,如果相等就返回true,不相等就返回false。
判断是否为空很简单,直接比较rear和front的值是否相等即可。
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->front==obj->rear;
}
置空函数
void myCircularQueueFree(MyCircularQueue* obj) {
free(obj->a);
free(obj);
}
获取队头元素
很简单,返回front位置的元素即可
int myCircularQueueFront(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
{
return -1;
}
else
{
return obj->a[obj->front];
}
}
获取队尾元素
这里就要思考一下了
如果rear不在数组第一个空间上,直接返回数组rear-1处的值即可,当rear位于数组首元素,就要返回数组第k个元素。
代码如下
int myCircularQueueRear(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
{
return -1;
}
else
{
if(obj->rear==0)
{
return obj->a[obj->k];
}
else{
return obj->a[obj->rear-1];
}
//下边是综合写法
//return obj->a[(obj->rear+obj->k)%(obj->k+1)];
}
}
出队列deQueue()
出队列只需要将front++即可,就算之前的数据不销毁,下次入队列操作也会覆盖他的数据。
代码如下
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
{
return false;
}
++obj->front;
obj->front%=(obj->k+1);
return true;
}
注意是要有返回值的,如果队列为空,就没有出数据,返回false,出数据成功就返回true。
入队列
代码如下:
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
if(myCircularQueueIsFull(obj))
{
return false;
}
obj->a[obj->rear]=value;
obj->rear++;
obj->rear%=(obj->k+1);
return true;
}
首先判断循环队列是否已满,如果已满就返回false,如果没有满就将rear位置的值改为value,然后rear++,判断是否超出范围,如果超出就置为0。最后入队列成功返回true。
到了这里这道题目就顺利解决了,如果使用双向链表来做这道题的话当然也可以,但是会稍微麻烦一点,有兴趣可以尝试尝试。
今天的内容就到这里啦,如果有错误欢迎各位指正哦!
综合上述代码后即可通过本题。
全部代码如下
typedef struct {
int* a;
int front;
int rear;
int k;
} MyCircularQueue;
MyCircularQueue* myCircularQueueCreate(int k) {
MyCircularQueue*obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
//多开一个方便区分空和满
obj->a=(int*)malloc(sizeof(int)*(k+1));
obj->k=k;
obj->front=obj->rear=0;
return obj;
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->front==obj->rear;
}
bool myCircularQueueIsFull(MyCircularQueue* obj) {
return (obj->rear+1)%(obj->k+1 )==obj->front;
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
if(myCircularQueueIsFull(obj))
{
return false;
}
obj->a[obj->rear]=value;
obj->rear++;
obj->rear%=(obj->k+1);
return true;
}
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
{
return false;
}
++obj->front;
obj->front%=(obj->k+1);
return true;
}
int myCircularQueueFront(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
{
return -1;
}
else
{
return obj->a[obj->front];
}
}
int myCircularQueueRear(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
{
return -1;
}
else
{
if(obj->rear==0)
{
return obj->a[obj->k];
}
else{
return obj->a[obj->rear-1];
}
//return obj->a[(obj->rear+obj->k)%(obj->k+1)];
}
}
void myCircularQueueFree(MyCircularQueue* obj) {
free(obj->a);
free(obj);
}
/**
* Your MyCircularQueue struct will be instantiated and called as such:
* MyCircularQueue* obj = myCircularQueueCreate(k);
* bool param_1 = myCircularQueueEnQueue(obj, value);
* bool param_2 = myCircularQueueDeQueue(obj);
* int param_3 = myCircularQueueFront(obj);
* int param_4 = myCircularQueueRear(obj);
* bool param_5 = myCircularQueueIsEmpty(obj);
* bool param_6 = myCircularQueueIsFull(obj);
* myCircularQueueFree(obj);
*/

