二叉树后根遍历的非递归算法——巧解

因为书上没有给出后序非递归算法，就去看了很多网上的后序遍历，都是照着定义死硬的遍历，复杂不讨好。如此，只能自力更生了

思路：

后根遍历的顺序是左子树>右子树>根，根是最后的，但我们整体遍历都是从根结点出发，这就很难去遍历。

那么我们可以换种思路，逆后根遍历，即根>右子树>左子树，

这样根就是最前的了，再把遍历结果逆转一下，就可以直接一次遍历！
逆后根遍历跟先根遍历几乎完全一样，原理一样，只是一个先往左一个先往右！

后根遍历的非递归算法——巧解（代码）：

	public void postOrderTraverse() {		//非递归算法的中根次序遍历
		LinkedStack> stack = new LinkedStack>();
		BinaryNode p = this.root;
		String str = "";
		
		while(p!=null||!stack.isEmpty()) {
			if(p!=null) {
				stack.push(p);
				str = (p.data+", ")+str;
				p=p.right;
			}
			else {
				p = stack.pop();
				p = p.left;
			}
		}
		System.out.println("后根次序遍历二叉树（非递归算法）：	"+str);
	}

放整体实现代码，部分无关其它方法就不一一实现了

这是先、中、后根遍历的代码：

package tree;

import LinkedList.LinkedStack;
import LinkedList.Node;
import Queue.LinkedQueue;

public class BinaryTree implements BinaryTTree {
	public BinaryNode root;
	public BinaryTree() {
		this.root = null;
	}

	public BinaryTree(T[] preList, T[] inList) {
		this.root = create(preList, inList, 0, 0, preList.length);
	}

	public BinaryNode create(T[] preList, T[] inList, int preStart, int inStart, int n){
		if(n<=0)
			return null;
		T elem = preList[preStart];
		BinaryNode p = new BinaryNode(elem);
		int i=0;
		while(i p) {
		if(p!=null) {
			System.out.print(p.data.toString()+", ");
			preOrder(p.left);
			preOrder(p.right);
		}
	}
	@Override
	public void inOrder() {
		System.out.print("中根次序遍历二叉树：	");
		inOrder(this.root);
		System.out.println();	
	}
	public void inOrder(BinaryNode p) {
		if(p!=null) {
			inOrder(p.left);
			System.out.print(p.data.toString()+", ");
			inOrder(p.right);
		}
	}

	@Override
	public void postOrder() {
		System.out.print("后根次序遍历二叉树：	");
		postOrder(this.root);
		System.out.println();	
	}

	public void postOrder(BinaryNode p) {
		if(p!=null) {
			postOrder(p.left);
			postOrder(p.right);
			System.out.print(p.data.toString()+", ");
		}
	}

	@Override
	public void levelOrder() {
		// TODO 自动生成的方法存根

	}

	@Override
	public BinaryNode search(T key) {
		// TODO 自动生成的方法存根
		return null;
	}

	@Override
	public BinaryNode getParent(BinaryNode node) {
		// TODO 自动生成的方法存根
		return null;
	}

	@Override
	public void insertRoot(T x) {
		// TODO 自动生成的方法存根

	}

	@Override
	public BinaryNode insertChild(BinaryNode p, T x, boolean leftChild) {
		// TODO 自动生成的方法存根
		return null;
	}

	@Override
	public void removeChild(BinaryNode p, boolean leftChild) {
		// TODO 自动生成的方法存根

	}

	@Override
	public void removeAll() {
		// TODO 自动生成的方法存根

	}

	public void preOrderTraverse() {		//非递归算法的中根次序遍历
		System.out.print("先根次序遍历二叉树（非递归算法）：	");
		LinkedStack> stack = new LinkedStack>();
		BinaryNode p = this.root;
		while(p!=null||!stack.isEmpty()) {
			if(p!=null) {
				stack.push(p);
				System.out.print(p.data+", ");
				p = p.left;
			}
			else {
				p = stack.pop();
				p = p.right;
			}
		}
		System.out.println();
	}

	public void inOrderTraverse() {		//非递归算法的中根次序遍历
		System.out.print("中根次序遍历二叉树（非递归算法）：	");
		LinkedStack> stack = new LinkedStack>();
		BinaryNode p = this.root;
		while(p!=null||!stack.isEmpty()) {
			if(p!=null) {
				stack.push(p);
				p=p.left;
			}
			else {
				p = stack.pop();
				System.out.print(p.data+", ");
				p = p.right;
			}
		}
		System.out.println();
	}
	
	public void postOrderTraverse() {		//非递归算法的中根次序遍历
		LinkedStack> stack = new LinkedStack>();
		BinaryNode p = this.root;
		String str = "";
		
		while(p!=null||!stack.isEmpty()) {
			if(p!=null) {
				stack.push(p);
				str = (p.data+", ")+str;
				p=p.right;
			}
			else {
				p = stack.pop();
				p = p.left;
			}
		}
		System.out.println("后根次序遍历二叉树（非递归算法）：	"+str);
	}
	
	public static void main (String[] arg) {
		String[] preList = {"A","B","D","G","C","E","F","H"};
		String[] inList = {"D","G","B","A","E","C","H","F"};
		BinaryTree bitree = new BinaryTree(preList,inList);
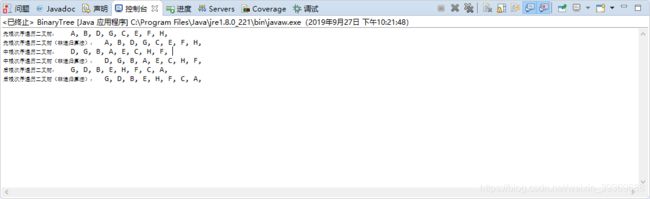
		bitree.preOrder();
		bitree.preOrderTraverse();
		bitree.inOrder();
		bitree.inOrderTraverse();
		bitree.postOrder();
		bitree.postOrderTraverse();
	}
}

注：
.toString()错误：调用的类对象（LinkedStack）没有实现toString()方法或者类对象的成员变量（BinaryNode）没有实现toString()方法

这里只需要实现BinaryNode类的toString()方法：
public String toString() {
		return (String)this.data;	
	}

实现结果截图