李宏毅老师浅谈机器学习

引例 - 宝可梦/数码宝贝 分类器

参数越多，训练的loss和testing售后的loss差距会越大
参数越多，越有可能overfitting

线条更复杂
edge detection，白色的点

根据线条的复杂程度
threshold（门槛）
h相当于network里面的参数

h有多少种可能的选择，也叫模型的复杂程度
含有未知数的模型，未知数的选择很多

如何定义损失函数？- 经验

这里定义一个直观的loss函数

定义一个loss
每一笔资料，代表h在这一笔资料上表现得好坏，算出来每一笔资料的loss，再取平均值

哪一个threshold的好坏

平均就是 错误率
一般不是这样定义loss，crossentropy
这样，直观但是，不能微分，不能通过gradient decent来optimize function

根据全体数据，得到最好的模型参数(理想）

假设可以搜索到全宇宙的宝可梦、数码宝贝
所有可能的h里面能让$D_{all}$ loss的平均值最小的那个取值
如果可以收集到所有的宝可梦和数码宝贝数据，那么可以得出最好的模型参数。
（这里用error rate不能微分但是没关系，h的可行性是有限的，才1w，爆搜就好）

但是，现实问题中，大多数问题只能收集到一部分样本（取样），并不能找到所有的样本数据。取样的要求：独立同分布（independently and identically distribution，i.i.d.）

如何衡量现实损失和理想损失接近程度？

差距越小越好

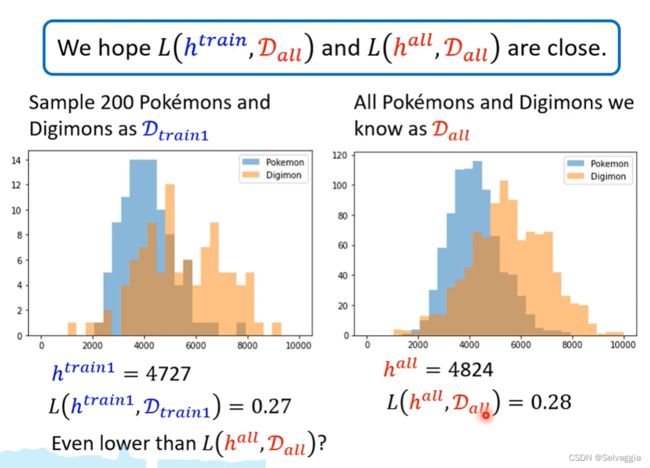
横轴越往右越复杂
纵轴表示在这个线条复杂度上的数码宝贝的数量
哈哈哈哈还记得h是什么吗？线条复杂度超过h就是数码宝贝，没超过就是个宝可梦喔

$L_{all}$在$D_{all}$上的loss一定小于$L_{train}$在$D_{all}$上的loss，
但可能$L_{train}$在$D_{train}$上的loss会小于$L_{all}$在$D_{all}$上的loss
但不一定会比其他threshold在其他训练集上得到的loss要小
为什么呢？

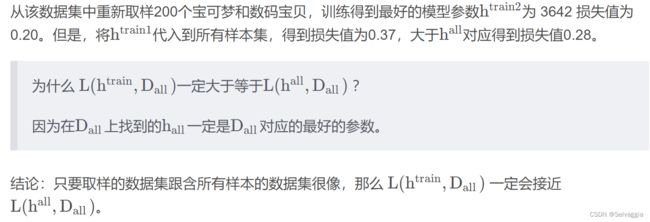
找一个比较有代表的D_train，不管是哪一个h，在D_train和D_all上的loss都差不多
看的是sample到怎样的序列，怎样一组D_train

如何得到跟含所有样本数据集很像的取样数据集？

接下来讨论的问题：如何得到跟含所有样本数据集很像的取样数据集？

只要满足②，就会得到一个跟含所有样本数据集很像的取样数据集，就一定满足①（即：达到目的：理想和现实的损失值接近）。

取样得到坏的数据集的概率多大？probablity of failure

接下来讨论的问题：取样得到坏的数据集的概率多大？

说明：
① 以下的讨论与模型没有关系，适用于深度学习或其他模型；
② 以下的讨论没有对数据假设任何的数据分布；
③以下的讨论与损失函数无关，适用于任何损失函数，因为分类和回归只是损失函数不同，所以以下讨论同时适用于分类和回归。

一般化的原理，适用于很多不同的情境下

一个点 一组训练资料 而不是一笔资料

蓝色 好的训练资料，理想和现实 差别小

橙色的点所占有的机率当然是越小越好，但怎么计算橙色的点占有的机率呢？
{为什么不看蓝色，因为判断一组训练资料是好还是不好，好的条件是：不管哪一个h，都能使得D_train和D_all上的loss都差不多(前者-后者不超过σ）,所有h都要满足，那证明一笔训练资料是坏的就只需要找到一个h使得前者-后者超过σ
}

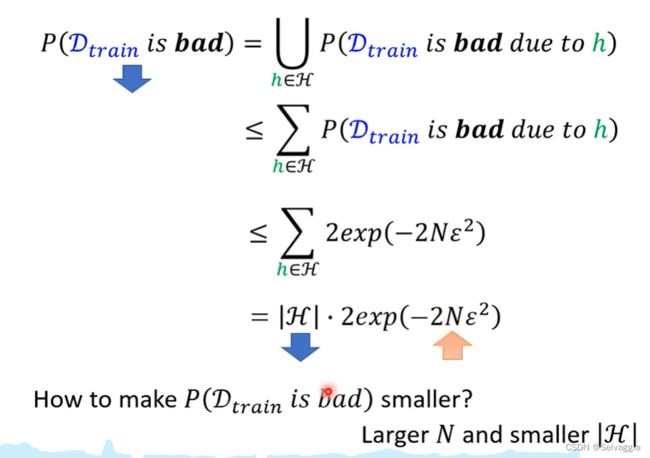
枚举所有样本集，计算是否是坏样本集，比较繁琐，所以使用如下方法，给定参数 h ，计算哪些样本集是坏样本集，并求出这些样本集占总样本集的概率。

很难考虑overlap的地方，overlap按道理得取并集嘛
不考虑overlap就直接求和，超过了1这个理论就无效了
求并集一定不会大于1，但是求和可能大于1，通常求和算出的P的上界都远远大于1，这时该理论无效。


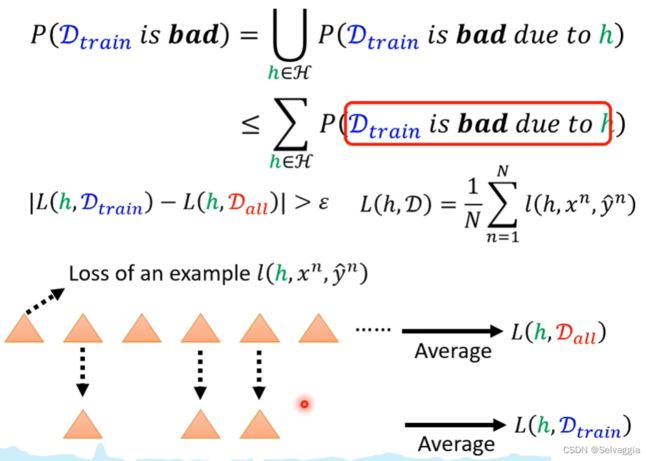
下图中，使用的是霍夫丁不等式

如何减小取样坏样本集的概率？- 增大样本集&减小参数可能值个数

如果要使得坏样本集的概率变小，有两种办法：一是增大样本集样本个数N；二是减小 h 可能值的个数。

给定某个h，会被它弄坏的那些D_train 出现的机率
L是D里面每一笔训练资料计算出的loss 的平均
如果增大N，那么，每一个h可以弄坏的training data，机率变少了，每一个h管的范围变少了（别忘了h是threshold），让差的dataset被sample到的机率变小

事实上，概率和 大于1常发生，不会特别把这些理论在实际中进行计算这个理论只是试图解释机器学习的原理，model的complexity和训练资料对结果会造成什么影响
理论很难派上用场

可以通过公式，计算出训练集中样本个数的下限N。

假设$\mathcal{H}$是有限的，即h（threshold是离散的），参数不应该是连续的吗？

H是有可能使用的function的数量
离散的，1~10000
但在training model里我们的参数不都是连续的吗，那H就是无穷大啊，式子无意义

解释一：计算机中没有绝对连续的数据，所有的计算都是连续的，精度是有限的

解释二：vc-dimension（描述模型复杂程度的指标），即使 $\mathcal{H}$ 是连续的，那么$\mathcal{H}$不一定是无穷大，还是有办法估计。

为什么实际情况中都是增大样本集使得理想和现实损失值接近，而不是减小$\mathcal{H}$？- 减小$\mathcal{H}$会导致找不到最佳参数

理想崩坏，那现实和理想再接近，也毫无意义

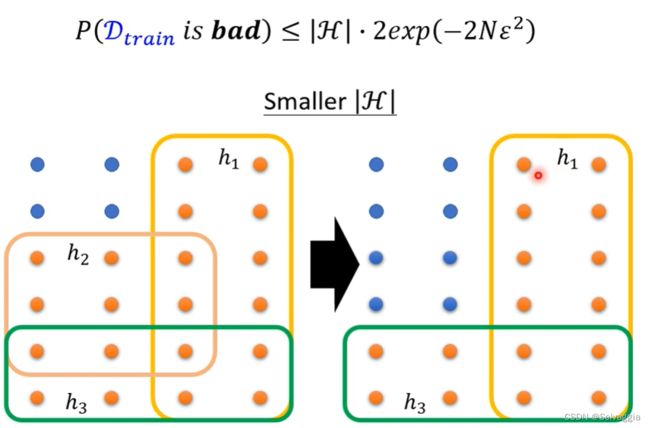
想要理想与现实接近，需要满足两个条件：① Larger N 大样本集；② smaller$\mathcal{H}$ 参数可选值少。

$\mathcal{H}$很小时，理想的损失值大，理想与现实的损失值差距小。
$\mathcal{H}$很大时，理想的损失值小，理想与现实的损失值差距大。

有没有办法使得现实的损失值小并且理想与现实的损失值差距也小？- 有，深度学习，how to do？To be continue

援引

造福后辈，前辈万岁！