哈夫曼树以及哈夫曼编码

    二叉树在数据是随机的时候，生成的树深度较低，左右两树可能也比较平衡，但是如果是有顺序的插入，那么二叉树深度就较高，要么子树全部在左边，要么子树全部在右边，那么由此引出最优二叉树，哈夫曼树

1、哈夫曼树含义

在权为w1,w2,,,,,,wn的n个叶子结点的所有二叉树中，带权路径长度wpl最小的二叉树称为赫夫曼树或最优二叉树。

什么是权？？

“权”就是“权重”的意思，可以理解为出现的频率，也可以理解为所占的比例，“权”在一定程度上提现了数据的分布规律。

1.1 路径和长度

在一颗树中，从一个节点往下可到达的孩子和孙子节点之间的通路称为路径。路径中分支的项目称为路径长度，若根节点的层数为1，则从根节点到L层节点的路径长度就是L-1。

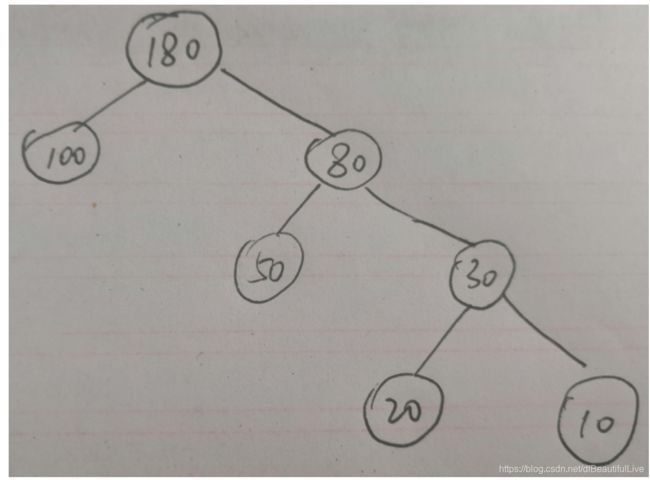
例：如上图，100和80的路径长度是1，50和30的路径长度是2，20和10的路径长度就是3

1.2 节点的权及带权路径长度

若将树中节点赋给一个有着某种含义的数值，则这个数值称为该节点的权。

节点的带权路径长度为：从根节点到该节点之间的路径长度与该节点的权的乘积

例：节点20的路径长度是3，它的带权路径长度=路径长度*权=3*20=60；

1.3 树的带权长度

树的带权路径长度规定为所有叶子节点的带权路径长度之和，记为wpl；

例子：树的wpl=1*100+2*80+3*20+3*10=350;

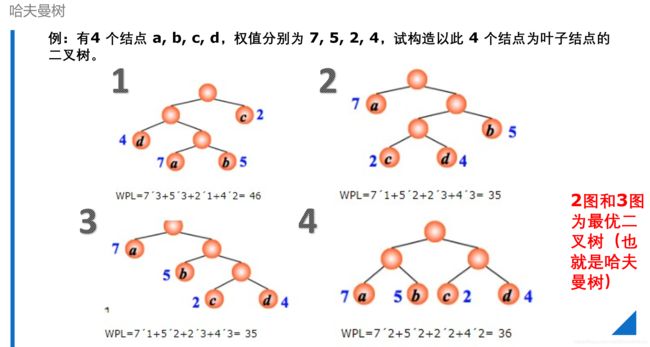
以下图片带权树取值最小的就是最优二叉树也就是哈夫曼树 。

2、哈夫曼树构造方式

1. 有4个节点A,B,C,D，权值分别为7,5,2,4，试构造以此4个节点为叶子节点的二叉树。

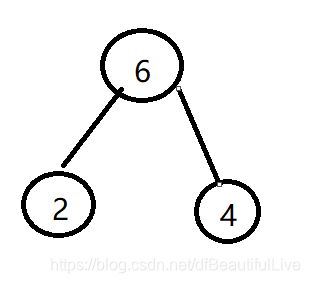
步骤一：先找到权值里最小的两个节点，那么就是2,4，将2,4构建树节点中，需要满足左小右大原则

步骤二：然后把2,4节点的和6添加到2和4的父节点上

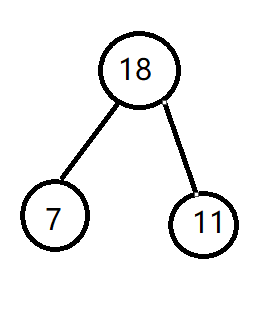
步骤三：然后节点就剩下7,5,6,再从7,5,6里找到两个最小的数，就是5,6，继续将5和6的和当父节点

步骤四：然后节点就剩下7,11，那就将最后两个数字构建一下，和为18成为父节点。

步骤五：将节点找到合在一起，最终生成了一个哈夫曼树

原则：哈夫曼树中权越大的叶子离根越近

3.哈夫曼编码

含义：哈夫曼（Huffman）编码属于码词长度可变的编码类，是哈夫曼在1952年提出的一种编码方法，即从下到上的编码方法。同其他码词长度可变的编码一样，可区别的不同码词的生成是基于不同符号出现的不同概率。

哈夫曼树的应用很广，哈夫曼编码就是其在电讯通信中的应用之一。广泛地用于数据文件压缩的十分有效的编码方法。其压缩率通常在20%～90%之间。在电讯通信业务中，通常用二进制编码来表示字母或其他字符，并用这样的编码来表示字符序列。

例：如果需传送的电文为 ‘ABACCDA’，它只用到四种字符，用两位二进制编码便可分辨。假设 A, B, C, D 的编码分别为 00, 01,10, 11，则上述电文便为 ‘00010010101100’（共 14 位），译码员按两位进行分组译码，便可恢复原来的电文。

数据的最小冗余编码问题（错误示例）

在上例中，若假设 A, B, C, D 的编码分别为 0，00，1，01，则电文 ‘ABACCDA’ 便为 ‘000011010’（共 9 位），但此编码存在多义性：可译为： ‘BBCCDA’、‘ABACCDA’、‘AAAACCACA’ 等。

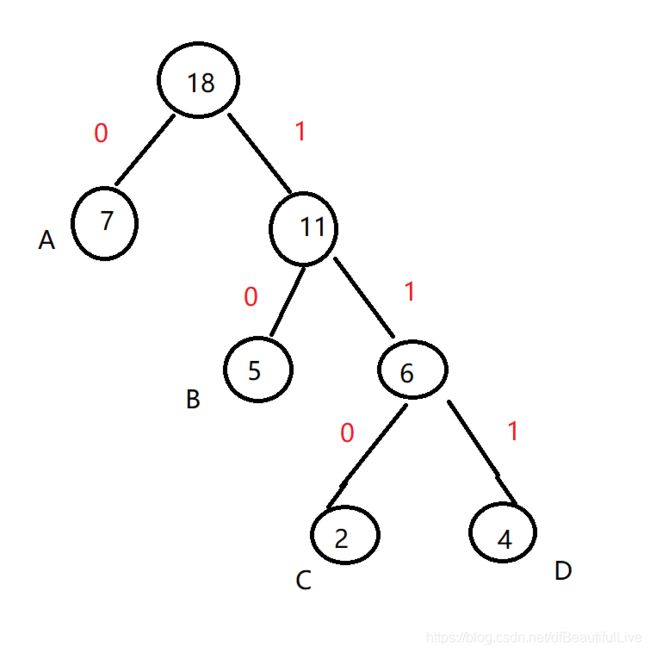
在树上标 “0” 和 “1” 规则是：左0 右1

每个字符的二进制编码为（从根节点 数到对应的叶子节点，路径上的值拼接起来就是叶子节点字母的应该的编码）

A:0        B:10       C:110     D:110

假如报文方发送11010111，接收方翻译为：“CBD”