题目及涉及的算法:
- 数字统计:入门题;
- 接水问题:基础模拟题;
- 导弹拦截:动态规划、贪心;
- 三国游戏:贪心、博弈论。
数字统计
题目链接:洛谷 P1179
这道题目是一道基础题。
我们只需要开一个变量 \(cnt\) 用于统计 \(2\) 出现的次数,然后从 \(L\) 到 \(R\) 去遍历每一个数 \(i\) ,对于 \(i\) 来说,我们去遍历它的每一位是不是 \(2\) ,如果是的话,则 \(cnt++\) 。最后输出 \(cnt\) 即可。
实现代码如下:
#include
using namespace std;
int cnt, L, R;
void solve(int a) {
while (a) {
if (a % 10 == 2) cnt ++;
a /= 10;
}
}
int main() {
cin >> L >> R;
for (int i = L; i <= R; i ++) solve(i);
cout << cnt << endl;
return 0;
} 接水问题
题目链接:洛谷 P1190
这道题目是一道标准的模拟题,它模拟了大家打开水的一个过程。
我们令 \(w[i]\) 表示第 \(i\) 个人打开水花费的时间;令 \(t[i]\) 表示当前第 \(i\) 个水龙头接水的人接好水的时刻。
那么一开始我们遍历比第 \(0\) 到 \(m-1\) 的坐标 \(i\) ,令 \(t[i] = w[i]\) (前 \(m\) 个人优先占领水龙头),
然后我们从 \(m\) 到 \(n-1\) 去遍历坐标 \(i\) ,对于第 \(i\) 个人,他应该插入的位置应该是所有 \(w[j](0 \le j \lt m)\) 中最小的那个 \(j\) ,我们假设最小的 \(w[j]\) 对应的坐标位 \(id\) ,那么第 \(i\) 个人将会插入到第 \(id\) 个位置。我们令 \(t[id] += w[i]\) 即可(这就表示第 \(i\) 个人进入到了第 \(id\) 个位置继续打开水)。
我们的最终答案就是所有的 \(t[i](0 \le i \lt m)\) 当中最大的那个(最大的那个 \(t[i]\) 对应最后一个打好的人打好的时间)。
实现代码如下:
#include
using namespace std;
const int maxn = 10010;
int n, m, cnt, w[maxn], t[maxn];
int main() {
cin >> n >> m;
if (m > n) m = n;
for (int i = 0; i < n; i ++) cin >> w[i];
for (int i = 0; i < m; i ++) t[i] = w[i];
for (int i = m; i < n; i ++) {
int id = 0; // id用于表示当前这一轮最早结束的那个队列对应的id
for (int j = 0; j < m; j ++) if (t[j] < t[id]) id = j;
t[id] += w[i];
}
int ans = 0;
for (int i = 0; i < m; i ++) ans = max(ans, t[i]);
cout << ans << endl;
return 0;
} 但是上面的代码并不是最优的,它的时间复杂度为 \(O(n \cdot m)\) 。
对于学过 堆(Heap) 这个数据结构的同学,我们可以使用堆来解决这个问题就可以了。我们可以维护一个大小不超过 \(m\) 的小根堆,每次从对顶取出来一个元素 \(t\) ,他表示最快的那个人打好开水的时间,然后如果接下来有人的话(假设该人的编号为 \(i\) ),我们再将 \(t + w[i]\) 放入堆中,直到所有的人都进堆。
然后我们再从堆中依次取出元素,堆中最后一个取出来的元素就对应最后一个打好开水的人打好的时间。
因为 堆 手动实现起来比较麻烦,所以我们这里使用 STL 容器提供给我们的 优先队列priority_queue 来实现一个小根堆。
实现代码如下:
#include
using namespace std;
int n, m, w, t, maxt;
priority_queue, greater > pq;
int main() {
cin >> n >> m;
if (m > n) m = n;
for (int i = 0; i < m; i ++) {
cin >> w; // w表示第i个人打开水所耗费的时间
pq.push(w);
}
for (int i = m; i < n; i ++) {
cin >> w;
t = pq.top();
pq.pop(); // 上一个人打好开水
pq.push(t + w); // 下一个人继续打开水
}
while (!pq.empty()) {
maxt = pq.top();
pq.pop();
}
cout << maxt << endl;
return 0;
} 导弹拦截
题目链接:洛谷 P1158
本题涉及算法:动态规划,贪心。不过主要还是一道 找规律 的题目(老师也没有找到规律,我是看了题解之后才找到规律的囧~)。
题解参考“安妮007”的洛谷博客:https://www.luogu.org/blog/Annie-007/solution-p1158
这道题首先要明确所有导弹不是被1号系统拦截就是被2号系统拦截
我们看到这道题的数据范围是10的5次方,大概是nlogn复杂度,联想到sort排序
让我们思考一下最优解,在最优解中1号系统肯定先拦下距离自己近的
如果1号去拦距离它远的导弹的话,其实就捎带脚的把近的导弹拦截了
如果我们把所有导弹按照对1号的距离进行升序排序,通过刚才的思考我们知道肯定是1号拦截一个前缀,剩下的后缀交给2号
那么我们枚举一下这个前缀和后缀的分界点即可(分界点我们此处定义为前缀的最后一个点)
前缀处理的1号系统代价比较好算,就是分界点到1号系统的距离
2号系统此时就不能再排序看后缀谁是最大的来计算代价,此时需要我们预处理出来一个数组,让d[i]=包括第i以及它后面的导弹中最远距离
实现代码如下:
#include
using namespace std;
const int maxn = 100010;
long long X1, Y1, X2, Y2, x, y, d[maxn];
int n;
struct Node {
long long s1, s2; // s1表示到(x1,y1)的距离;s2表示到(x2,y2)的距离
} a[maxn];
bool cmp(Node a, Node b) {
return a.s1 < b.s1;
}
int main() {
cin >> X1 >> Y1 >> X2 >> Y2 >> n;
for (int i = 0; i < n; i ++) {
cin >> x >> y;
a[i].s1 = (x - X1) * (x - X1) + (y - Y1) * (y - Y1);
a[i].s2 = (x - X2) * (x - X2) + (y - Y2) * (y - Y2);
}
sort(a, a+n, cmp);
for (int i = n-1; i >= 0; i --) {
d[i] = max(a[i].s2 , d[i+1]);
}
long long ans = LONG_LONG_MAX;
for (int i = 0; i < n; i ++)
ans = min(ans, a[i].s1 + d[i+1]);
cout << ans << endl;
return 0;
} 三国游戏
题目链接:洛谷 P1199
本题涉及算法:贪心、博弈论。
题解来自 wjyyy 的博客:https://www.luogu.org/blog/wjyyy/solution-p1199
这个题尽管题目长,主要还是证明贪心的正确性。
首先注意到,在这个题里,计算机是 贪心的 ,也就是说,无论人选什么,它都会尽可能去选与人默契值最大的。想到这里可能会联想到博弈论,因为两个人的目标都是一样的。不过稍加分析会发现,人总是拿不到最优的。
因为我们选将可以看作一个配对的过程,所以在选将 ii 后,第 ii 行和第 ii 列表格中行和列都是我们的,在自己的行和自己的列交点处就是自己的武将对了。也就是说表格是对称的。
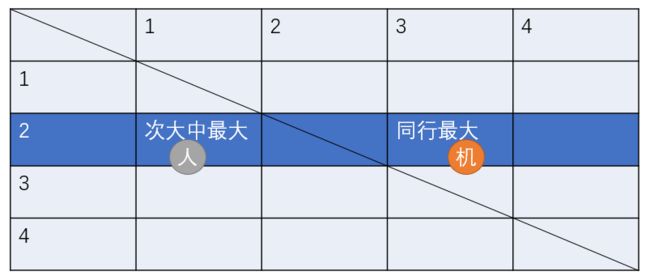
分析样例可以得知,最优解总是 每一行(整理后)排名第二大 中最大的那个。也就是说,每一行的最大的那一组电脑是不可能让你选到手的。一旦选择了最大的一组中的其中一个,电脑总可以先手把另一半抢掉,所以每行最大的一组是不可能选出的。而我们要证明次大中最大的那个是一定可以选到的。
当我们选择了次大中最大的那一行,电脑就毫无疑问会把那一行中最大的一个给选出来。
此时我们把次大中最大的另一半给配上就可以了。那我们现在拿到了人所可能拿到的最大的一对武将,怎么保证计算机不拿到比自己更大的武将呢?可以看出,比当前已有的默契值更大的武将一定在其他行中处于最大的位置,(假设计算机足够聪明)如果计算机去选了那个位置,人先手去把它抢掉就行了。而计算机并没有那么聪明,它只会避免你去选能选的最大的武将,此时可以分情况讨论。
计算机此时选择一个武将有两种影响:一是与原来的绿线相交,如果与绿线相交会直接确定一组武将,此时人是阻止不了的。但是我们可以保证现在一条线与绿线的交点值一定小于人的答案。 反证: 如果那个值比人的答案(五角星)要大而比三角形要小,那么次大中最大的就是这个值,因此这个值不可能在这个范围;而如果那个人的值比三角形还大,那次大中最大的就是三角形了。因此与绿线的交点绝不会超过五角星。
第二种影响就是不与绿线相交。对于不与绿线相交的部分,只要人去把计算机最大的抢掉,计算机就不可能抢到每一行中最大的那个。
综上所述,无论人还是计算机都无法抢到每一行中最大的那个,而根据贪心,人去选每行次大元素中最大的一定能选到,此时也能阻止计算机去选更大的元素。同时人不会输。
该博客实现代码如下:
#include
#include
using std::sort;
int a[510][510];
int main()
{
int n;
scanf("%d",&n);
for(int i=1;ia[i][n-1]?ans:a[i][n-1];//选出排名第二中最大的那个
}
printf("1\n%d\n",ans);//一定有解
return 0;
} 然后我看了一下我之前实现的时候得分 90 的代码,如果我最后不判断我的得分和机器人的得分,直接输出“1”和我的得分,我是能够AC的;
但是在第2组测试数据的时候我的程序好像是测出了我的得分小于机器人的得分,所以下面目前是我能够AC得代码,但是我目前的思路是倒数第5、6行的,而不是倒数第3、4行的。我寻思接下来有时间再好好思考一下,争取尽快解决这个问题。
实现代码如下(虽然AC了但是最后输出的结果还是有一些疑问):
#include
using namespace std;
const int maxn = 550;
int g[maxn][maxn], n, belong[maxn];
vector vec, ans1, ans2;
int get_company(int id) {
int tmp1 = 0, tmp2 = 0;
for (int i = 1; i <= n; i ++) {
if (id == i || belong[i]) continue;
if (g[id][i] > tmp1) { tmp2 = tmp1; tmp1 = g[id][i]; }
else if (g[id][i] > tmp2) tmp2 = g[id][i];
}
for (vector::iterator it = ans1.begin(); it != ans1.end(); it ++) {
int u = *it;
tmp2 = max(tmp2, g[id][u]);
}
return tmp2;
}
bool cmp1(int a, int b) {
return get_company(a) > get_company(b);
}
bool cmp2(int a, int b) {
int sz = ans1.size();
int tmp1 = 0, tmp2 = 0;
for (int i = 0; i < sz; i ++) {
tmp1 = max(tmp1, g[ ans1[i] ][a]);
tmp2 = max(tmp2, g[ ans1[i] ][b]);
}
return tmp1 > tmp2;
}
int main() {
cin >> n;
for (int i = 1; i <= n; i ++) {
for (int j = i+1; j <= n; j ++) {
cin >> g[i][j];
g[j][i] = g[i][j];
}
}
for (int i = 1; i <= n; i ++) vec.push_back(i);
for (int i = 1; i <= n; i ++) {
if (i % 2) {
sort(vec.begin(), vec.end(), cmp1);
ans1.push_back(vec[0]);
belong[ vec[0] ] = 1;
vec.erase(vec.begin());
}
else {
sort(vec.begin(), vec.end(), cmp2);
ans2.push_back(vec[0]);
belong[ vec[0] ] = 2;
vec.erase(vec.begin());
}
}
int res1 = 0, res2 = 0;
for (int i = 0; i < n/2; i ++)
for (int j = i+1; j < n/2; j ++) {
res1 = max(res1, g[ ans1[i] ][ ans1[j] ]);
res2 = max(res2, g[ ans2[i] ][ ans2[j] ]);
}
// puts(res1 >= res2 ? "1" : "0");
// if (res1 >= res2) cout << res1 << endl;
puts("1");
cout << res1 << endl;
return 0;
}