A*算法求解N数码问题(AI实验一)
1.实验题目
A*算法求解N数码问题,要求程序内,输入给定初始状态和目标状态,输出所需步数,过程状态及时间(程序可直接运行,无需再手动输入)。
2.实验目的及要求
- 熟悉和掌握启发式搜索的定义、估价函数和算法过程
- 利用A*算法求解N数码难题,理解求解流程和搜索顺序
- 熟练掌握numpy库的相关函数
3.实验原理
A*算法是一种启发式图搜索算法,其特点在于对估价函数的定义上。对于一般的启发式图搜索,总是选择估价函数f值最小的结点作为扩展结点。因此,f是根据需要找到一条最小代价路径的观点来估算结点的,所以,可考虑每个结点n的估价函数值为两个分量:从起始结点到结点n的实际代价以及从结点n到达目标结点的估价代价。
启发式图搜索的基本特点:如何寻找并设计一个与问题有关的h(n)以及构出f(n)=g(n)+h(n),然后以f(n)的大小来排列待扩展状态的次序,每次选择f(n)的最小值进行扩展。
- open表:保留所有已生成而未扩展的状态
- closed表:记录已扩展后的状态
进入open表的状态是根据估值的大小插入到表中合适的位置,每次从表中优先取出启发估价函数值最小的状态加以扩展。
4.实验内容
- 以8数码问题为例实现A*算法的求解程序
original state:
| 2 | 8 | 3 |
|---|---|---|
| 1 | 6 | 4 |
| 7 | 5 |
target state:
| 1 | 2 | 3 |
|---|---|---|
| 8 | 4 | |
| 7 | 6 | 5 |
估价函数f(n)=g(n)+h(n)
g(n)=d(n) ------结点n在搜索树中的深度
h(n)可选择h1(n) — 结点n中“不在位”的数码个数 或 h2(n)=p(n)–当前状态到终点的曼哈顿距离
2. 在求解8数码问题的A* 算法程序中,设置相同的初始状态和目标状态,针对不同的估价函数,求得问题的解,并比较它们对搜索算法性能的影响,包括扩展结点数、生成结点数等
3. 画出A*算法求解框图
5.实验分析
每移动一次空格,就产生一种状态。使用BFS来搜索,但这里使用优先队列而不是普通的队列,这样就可以利用A*算法的核心——评估函数f(n)=g(n)+h(n),对每一种状态用评估函数进行优先队列的排序(只要你给了评估函数的值,优先队列会自己帮我们排序)。
搜索过程如下:
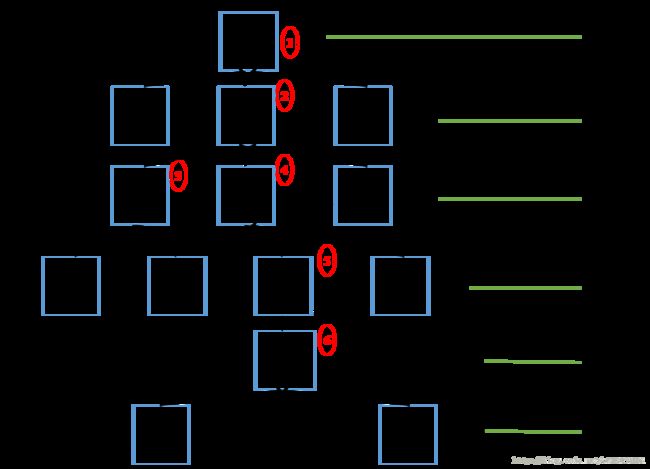
6.代码实现
from queue import PriorityQueue
import datetime
class node:
def __lt__(self,other):
return self.cost < other.cost
def __init__(self,n,s,p):
self.num = n#str的数组
self.step = s#当前已经走了的步数,int
self.zeroPos = p#0的位置,int
self.cost = 0
self.parent = None#父指针
self.setCost()
def setCost(self):
global des
count = 0
for i in range(len(des)):
if self.num[i] != des[i]:
count += 1
self.cost = count + self.step
def setParent(self,father):
self.parent = father
def swap(li,first,second):
temp = li[first]
li[first] = li[second]
li[second] = temp
def format_p(s,N):
for i in range(N):
print('\t'.join(s[i*N:(i+1)*N]))
print()
def makeChangeId(N):
#根据N实现changeId
li = []
MAX = N**2
for i in range(MAX):
temp = []
row = i//N#行
col = i%N#列
if row is not 0:#上,如果行为0,那么肯定不往上移动了
temp.append(i-N)
else:
temp.append(-1)
if col is not 0:#左
temp.append(i-1)
else:
temp.append(-1)
if row is not N-1:#下
temp.append(i+N)
else:
temp.append(-1)
if col is not N-1:#右
temp.append(i+1)
else:
temp.append(-1)
li.append(temp)
return li
def bfs(start,zeroPos):
#start is str's list
#zeroPos is int
global changeId,visit,que,des,N
#该函数返回最后一个状态即最后一个node
startNode = node(start,0,zeroPos)
que.put(startNode)
while(not que.empty()):
outNode = que.get()
strList = outNode.num#这里是list
strTuple = tuple(strList)#状态表示,这里是tuple
if strTuple in visit:
continue
visit[strTuple] = 1
pos = outNode.zeroPos#零的位置
for i in range(4):
if changeId[pos][i] != -1:
swap(strList,pos,changeId[pos][i])
joinTuple = tuple(strList)
if strList == des:
print('bingo')
swap(strList,pos,changeId[pos][i])
#找到了先交换回去,因为这里strList是状态对象的成员了,直接返回的话,就不会执行
#下面那句swap了,所以这里得加上一句swap
return outNode
if joinTuple not in visit:
new = node(strList.copy(),outNode.step+1,changeId[pos][i])
#注意这里必须使用copy,因为不复制传进去的就只是个引用,会导致所有node的成员都是同一个list
new.setParent(outNode)
que.put(new)
swap(strList,pos,changeId[pos][i])
visit = dict()
que = PriorityQueue()
print('Please input N:')
N = eval(input())
print('Please input the original state:')
src = input().split()#和之前不同,这里存的都是str的list
print('Please input the target state:')
des = input().split()
for i in range(len(src)):
if src[i] == '0':
break
start_t = datetime.datetime.now()
changeId = makeChangeId(N)
last = bfs(src,i)
result = [des]#先装des,用作栈使用
def findroot(last,result):
result.append(last.num)
if last.parent == None:
return
else:
findroot(last.parent,result)
findroot(last,result)
end_t = datetime.datetime.now()
print('The transition from original state to the target state:')
while(len(result)):
format_p(result.pop(),N)
print('Step number:'+str(last.step+1)+'steps')
print("time = ", (end_t - start_t).total_seconds(), "s")
print('end')