学习笔记|两因素重复测量的方差分析|主体内效应|主体间效应|流程图|《小白爱上SPSS》课程:SPSS第十讲 | 两因素重复测量的方差分析(史上最全,做实验的看过来)
目录
- 学习目的
- 软件版本
- 原始文档
- 两因素重复测量的方差分析
-
- 一、实战案例
- 二、统计策略
- 三、SPSS操作
-
- 1、正态性检验
- 2、方差分析
- 四、结果解读
-
- 第一,描述性统计
- 第二, 多变量检验。
- 第三,球形检验结果
- 第四张, 主体内效应检验(重点掌握)
- 第五张,主体间效应检验(重点掌握)
- 五、简单效应操作及结果
-
- 1、SPSS操作
- 2、结果解读
- 六、规范报告
-
- 1、规范表格
- 2、规范文字
- 重复测量方差分析流程图
- 划重点
学习目的
SPSS第十讲 | 两因素重复测量的方差分析(史上最全,做实验的看过来)
软件版本
IBM SPSS Statistics 26。
原始文档
《小白爱上SPSS》课程
#统计原理
两因素重复测量的方差分析
在科学研究中,经典实验设计是常用的实验范式,即将研究对象随机分成实验组和对照组,分别对两组进行前后测试,来比较实验干预效果。
然而,如果仅仅比较前后两次测试结果,那么就无法获知测量指标在实验研究过程中的趋势变化。因此,有条件的话,有必要将过程中的测量数据也纳入研究,以更深入了解测量指标的时间变化趋势、不同时段的实验效果等。
重复测量的实验设计有很多种,这一讲主要以两因素重复测量实验设计为例进行方差分析。其中因素1为组别,为组间变量;因素2为测量次数,为组内变量。这种设计也称为混合实验设计。
同样,如同两因素析因设计方差分析一样,我们能分析各实验因素的主效应、交互效应和简单效应(啥主效应、交互效应?点击复习:第九讲 | 两因素析因设计的方差分析)。
一、实战案例
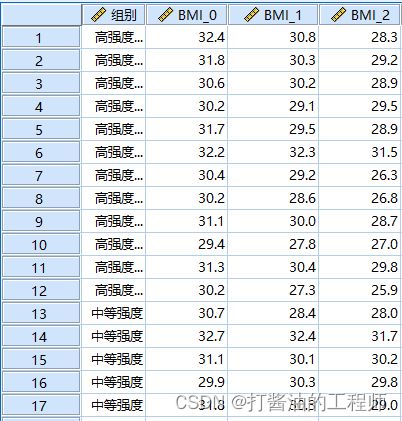
小白想了解高强度间歇运动的减肥效果,随机抽取了24名肥胖大侠,随机分配到高强度间歇运动组和中等强度有氧运动组。要求两组每天运动30分钟,持续干预12周。用BMI值衡量肥胖水平,BMI值共测试了3次:干预前的BMI值(BMI_0)、干预6周的BMI值(BMI_1)和干预12周结束的BMI值(BMI_2)。获得部分数据如下。
问:高强度间歇运动和中等强度运动对减肥有无作用?
读取数据:
GET
FILE='E:\E盘备份\recent\小白爱上SPSS\小白数据\第十讲 两因素重复测量方差分析.sav'.
二、统计策略
统计分析策略口诀“目的引导设计,变量确定方法”。
针对上述案例,扪心六问。
Q1:本案例研究目的是什么?
A:比较差异。
Q2:本案例属于什么研究设计?
A:两因素重复测量实验设计
Q3:有几个变量?
A:有三个变量。
自变量1为运动干预,属于组间变量,分成两个水平:高强度间歇和中等强度;
自变量2为测试次数,属于组内变量,重复测量了三次;
因变量为BMI值,连续型变量。
Q4:变量类型是什么?
A:自变量1和自变量2均为分类变量
BMI值为连续型变量。
Q5:各组数据服从正态分布么?
A:需要检验。
若服从,采用两组重复测量方差分析;
如不服从正态,则采用Scheirer–Ray–Hare检验(目前SPSS统计软件没有提供Scheirer-Ray-Hare 检验,需要借助其他软件,比如R软件、SAS软件实现)。
Q6:组内各水平数据是否满足球形对称假设?
A:需要检验。
若不满足,可查看一元矫正或多元方差分析结果。
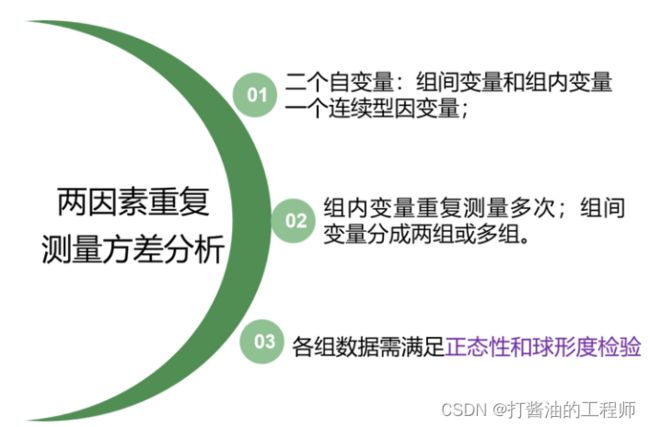
概括而言,如果数据满足以下条件,则采用两因素重复测量的方差分析。
三、SPSS操作
1、正态性检验
本案例需要对六组都进行正态性检验。
命令行:
EXAMINE VARIABLES=BMI_0 BMI_1 BMI_2 BY 组别
/PLOT HISTOGRAM NPPLOT /*若无此行,则不输出正态性检验表*/
/COMPARE GROUPS
/STATISTICS DESCRIPTIVES
/CINTERVAL 95
/MISSING LISTWISE
/NOTOTAL.

经S-W(夏皮洛-威尔克)检验,发现各组p均大于0.05,无统计学意义,原假设(数据按正态分布)成立,服从正态分布,可采用重复测量方差分析。
2、方差分析
Step1:依次点击“分析——一般线性模型——重复测量”。
Step2:在弹出“重复测量定义因子”对话框,将“主体内因子名”中的因子1,修改为测量次数。“级别数”框中输入重复测量次数“3”,单击“添加”按钮。选择左下角的“定义”按钮。
Step3: 在弹出的“重复测量”对话框。将3次测量变量“BMI_0”、“BMI_1”和“BMI_2”按照框中测量的顺序,逐个放入“主体内变量”。也可以按Shift键,将3个变量全部选中一次性放入。
同时将“组别”放入“主体间因子”中。
Step4:点击“模型”,出现“重复测量:模型”对话框,默认选择“全因子”。全因子表明会输出组别主效应、测量次数主效应、以及两者的交互效应。
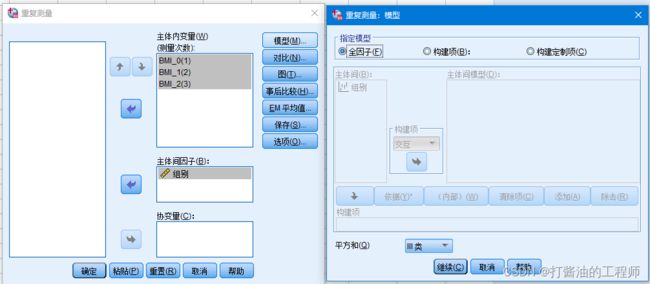
Step5:点击“图”,出现“重复测量:轮廓图”对话框。我们将“组别”放入“水平轴”对话框,将“测量次数”放入“单独线条”对话框,点击“添加”。这就可以绘制以“组别”为X轴,分成两组的折线图。
同时反过来,将“测量次数”放入水平轴,“组别”放入“单独线条”对话框,再绘制一条以“测量次数”为X轴的图。点击“继续”。
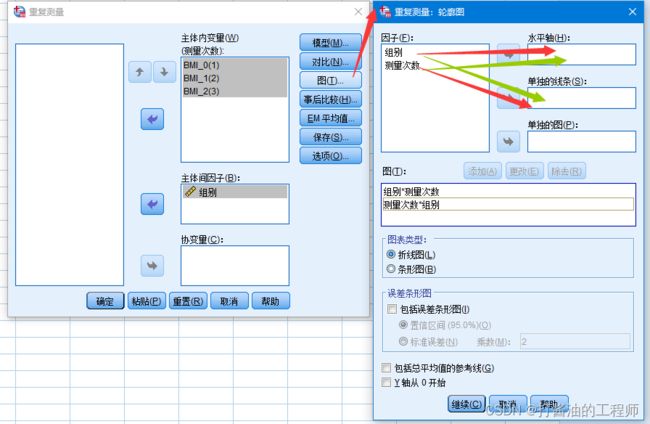
Step6:单击右侧的“EM平均值”按钮,弹出“估计边际平均值”按钮。将“组别”、“测量次数”和“组别*测量次数”全部移至右侧的“显示下列各项的平均值”框中,并将“比较主效应”复选框勾选上,同时选择“邦弗伦尼”比较。设置完后,点击“继续”。

Step7:点击“选项”,出现“选项”对话框。主要勾选“描述统计”和“效应量估计”。
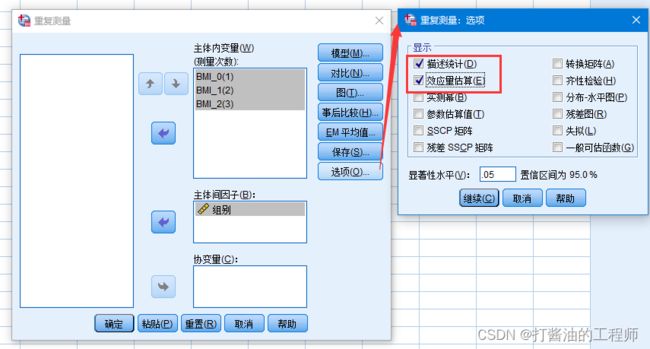
Step8:点击“继续”和“确定”,就能输出结果。
命令行:
GLM BMI_0 BMI_1 BMI_2 BY 组别
/WSFACTOR=测量次数 3 Polynomial
/METHOD=SSTYPE(3)
/PLOT=PROFILE(组别*测量次数 测量次数*组别) TYPE=LINE ERRORBAR=NO MEANREFERENCE=NO YAXIS=AUTO
/EMMEANS=TABLES(组别) COMPARE ADJ(BONFERRONI)
/EMMEANS=TABLES(测量次数) COMPARE ADJ(BONFERRONI)
/EMMEANS=TABLES(组别*测量次数)
/PRINT=DESCRIPTIVE ETASQ
/CRITERIA=ALPHA(.05)
/WSDESIGN=测量次数
/DESIGN=组别.
四、结果解读
重复测量的结果有多个表格,在此讲解几个重点表格。
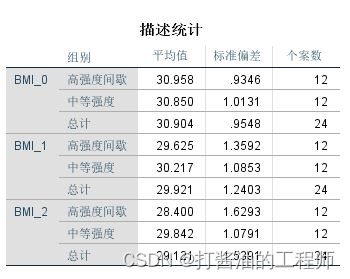
第一,描述性统计
第二, 多变量检验。
该表格是将三次重复测量结果作为三个因变量,进行多因变量的方差分析。
然而,是否以此检验结果为准,应依据球形性检验(第三张表格)。如果不符合球形检验,则以此多变量检验结果或者以一元方差分析中校正结果为准。
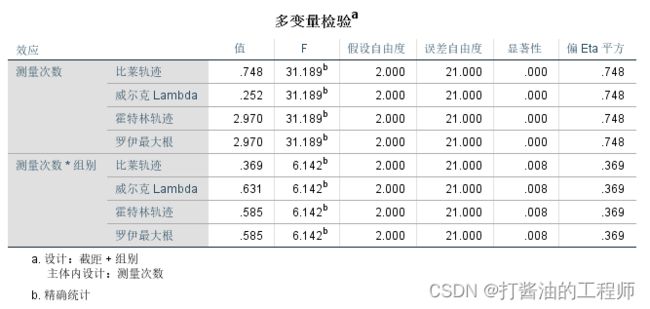
从表中可看出,表中呈现了比莱轨迹、威尔克Lambda、霍特林轨迹和罗伊最大根四种检验方法,他们检验结果的F值和p都一致,我们一般选择比莱轨迹结果就好了。
结果显示:测量次数的主效应显著,F=31.189,p<0.001,偏η2=0.748;
测量次数与组别的交互效应显著,F=6.142,p<0.008,偏η2=0.369。
说明下,偏η2是指效应量,现在越来越多的杂志要求报告效应量。
第三,球形检验结果
Machly W=0.688,显著性p=0.02<0.05, 具有统计意义,不符合原假设(能通过球形检验),不符合球形检验。因此,应以多变量检验结果或者以一元方差分析中校正结果为准。
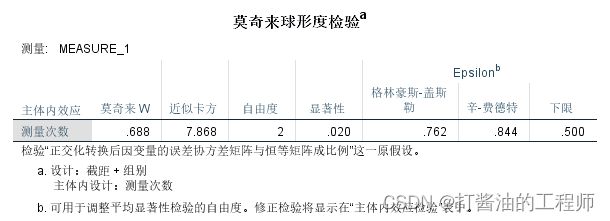
第四张, 主体内效应检验(重点掌握)
本例不符合球形检验,因此,建议查看第二行“Greenhouse-Geisser”检验结果(事实上,本例中四种检验结果的F值和p是一致的,只是自由度不一样)
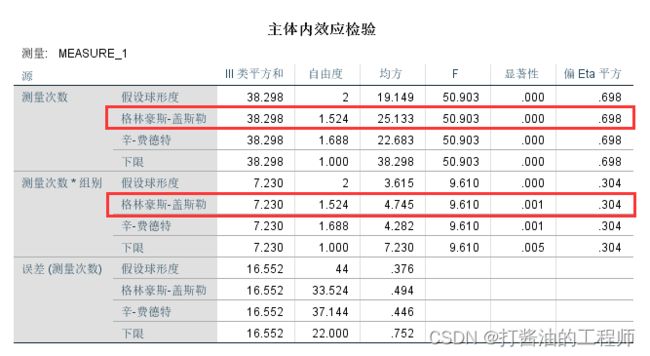
结果显示,测量次数的主效应显著,F=50.903,p<0.001,偏η2=0.698;
测量次数与组别的交互效应显著,F=9.610,p=0.001,偏η2=0.304。
第五张,主体间效应检验(重点掌握)
从表格中可知,组别的主效应不显著,F=2.047,p=0.167,偏η2=0.085。
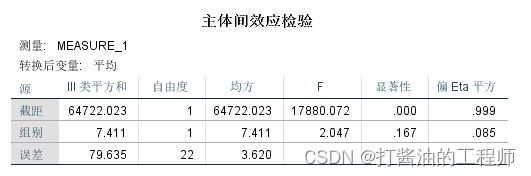
针对两因素重复测量方差分析,其统计分析策略如下。
(1) 如果自变量之间不存在交互效应,着重分析主效应;
(2) 如果自变量之间存在交互效应,着重分析简单主效应。
本案例交互效应显著,故着重分析交互效应和简单效应。
五、简单效应操作及结果
1、SPSS操作
Step1:回到上述“重复测量”窗口,点击“粘贴”。
Step2:弹出IBM SPSS Statistics 语法编辑器界面,这里呈现的是之前所有菜单式操作的计算机语言。
Step3:在/EMMEANS=TABLES(组别*测量次数),按【回车键】,另起一行,输入或者复制粘贴以下语句:
/EMMEANS=TABLES(组别*测量次数)COMPARE(组别)ADJ(BONFERRONI)
/EMMEANS=TABLES(组别*测量次数)COMPARE(测量次数)ADJ(BONFERRONI)
GLM BMI_0 BMI_1 BMI_2 BY 组别
/WSFACTOR=测量次数 3 Polynomial
/METHOD=SSTYPE(3)
/PLOT=PROFILE(组别*测量次数 测量次数*组别) TYPE=LINE ERRORBAR=NO MEANREFERENCE=NO YAXIS=AUTO
/EMMEANS=TABLES(组别) COMPARE ADJ(BONFERRONI)
/EMMEANS=TABLES(测量次数) COMPARE ADJ(BONFERRONI)
/EMMEANS=TABLES(组别*测量次数)
/EMMEANS=TABLES(组别*测量次数)COMPARE(组别)ADJ(BONFERRONI)
/EMMEANS=TABLES(组别*测量次数)COMPARE(测量次数)ADJ(BONFERRONI)
/PRINT=DESCRIPTIVE ETASQ
/CRITERIA=ALPHA(.05)
/WSDESIGN=测量次数
/DESIGN=组别.
解释:
①TABLES(组别*测量次数)指的是“组别”与“测量次数”的交互效应;
②COMPARE(组别)是指根据“测量次数”变量提供简单主效应结果,就是固定组别某一个水平,如在高强度间歇条件下,比较重复测量三次的BMI值之差异,需采用多重比较。
③ADJ(BONFERRONI) 多重比较的调整方法,一般选择LSD、Bonferroni、SIDAK调整。本案例选择Bonferroni调整。
Step4:点击“运行”——“全部”。即可呈现简单效应结果。
2、结果解读
第一张,组别简单效应,看4. 组别 * 测量次数下的单变量检验:
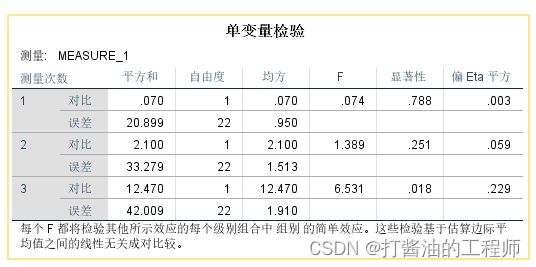
结果显示:
在前测中,组别的简单效应不显著,F=0.074,p=0.788, 偏η2=0.003;
在中测中,组别的简单效应不显著,F=1.389,p=0.251, 偏η2=0.059;
在后测中,组别的简单效应显著,F=6.531,p=0.018, 偏η2=0.229;
第二张,看4. 组别 * 测量次数下的成对比较结果:
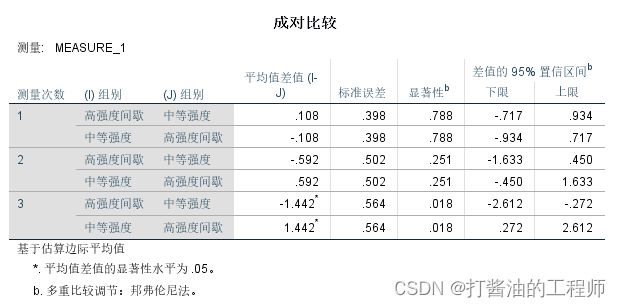
由于组别只有两个水平,即高强度间歇和中等强度,虽然我们选择了BONFERRONI矫正,实际上并没有多重比较和矫正。而且成对比较结果的p值与上一张表格的简单效应p值是一样的。
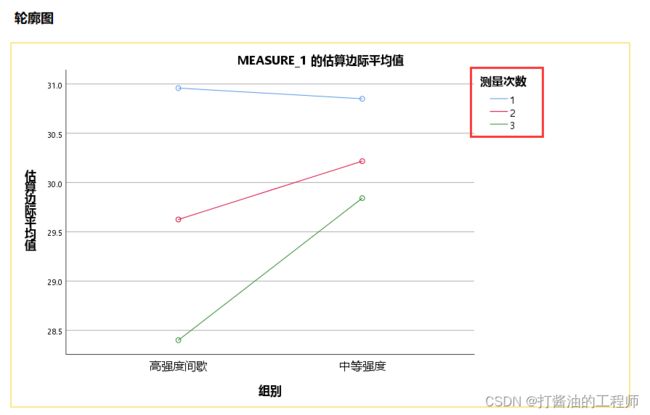
组别的简单效应结果如下图所示:
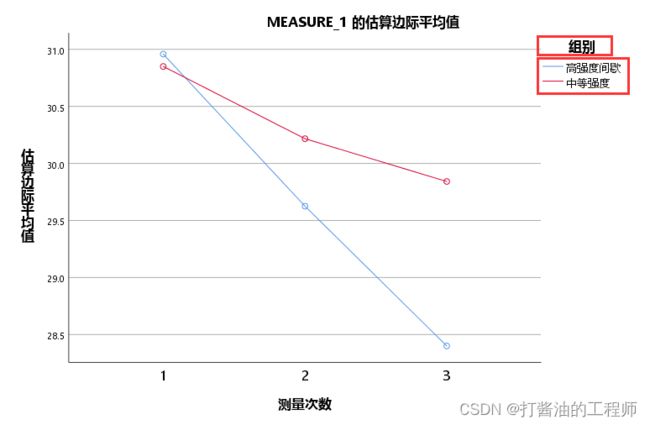
第三张, 测量次数的检验效应
由于测量次数是组内变量,SPSS只给出多变量结果。
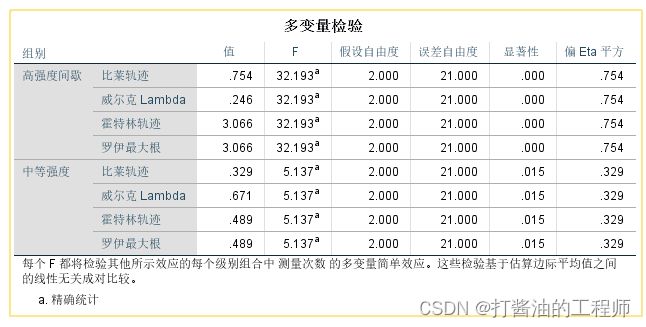
结果显示:
在高强度间歇下,测量次数的简单效应显著,F=32.193,p<0.001, 偏η2=0.754;
在中等强度下,测量次数的简单效应显著,F=5.137,p=0.015, 偏η2=0.329;
由于测量次数有三个水平,到底哪两两之间有显著性差异呢?要查看成对比较。
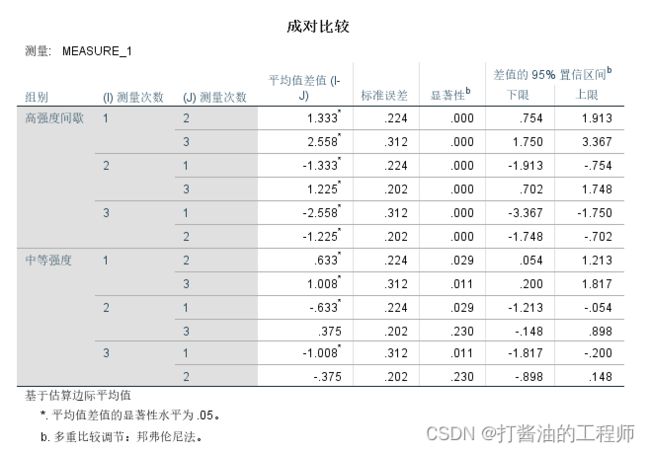
成对比较结果显示,
在高强度间歇条件下,前测、中测和后测BMI值依次下降,均达到显著性水平(p<0.001);
在中等强度条件下,前测的BMI值显著高于中测(p=0.029)和后测(p=0.011);
而中测和后测的BMI值无显著性差异(p=0.230)。
测量次序的简单效应结果如下图所示:
六、规范报告
规范报告有多种方式,本公众号只提供一种方式供参考。
1、规范表格
2、规范文字
经S-W(夏皮洛-威尔克)检验,各组数据服从正态分布。另球形检验结果,其中Machly W=0.67,显著性p=0.02, 不符合球形检验。因此,以一元方差分析“Greenhouse-Geisser”中校正结果为准。
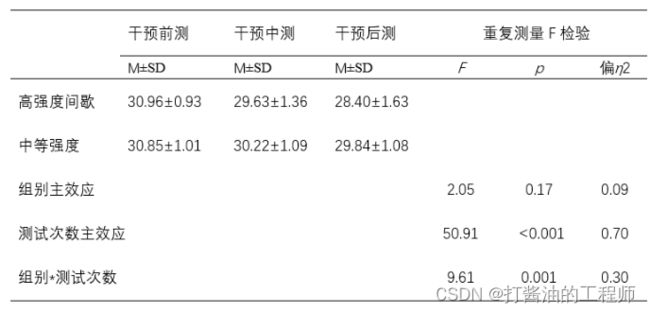
重复测量方差分析结果显示:
组别的主效应不显著,F=2.05,p=0.17,偏η2=0.09;
测量次数的主效应显著,F=50.91,p<0.001,偏η2=0.70;
测量次数与组别的交互效应显著,F=9.61,p=0.01,偏η2=0.304。
组别简单效应检验结果显示:
在干预前测,组别的简单效应不显著,F=0.074,p=0.788, 偏η2=0.003;
在干预中测,组别的简单效应不显著,F=1.389,p=0.251, 偏η2=0.059;
在干预后测,组别的简单效应显著,F=6.531,p=0.018, 偏η2=0.229;
测量次数简单效应检验结果显示:
在高强度间歇条件下,测量次数的简单效应显著,F=32.19,p<0.001, 偏η2=0.76;
在中等强度条件下,测量次数的简单效应显著,F=5.14,p=0.015, 偏η2=0.33;
多重比较发现:
在高强度间歇条件下,前测、中测和后测的BMI值依次下降,均达到显著性水平(p<0.001);
在中等强度条件下,前测的BMI值显著高于中测(p=0.029)和后测(p=0.011)BMI值,而中测与后测的BMI没有显著性差异(p=0.230)。
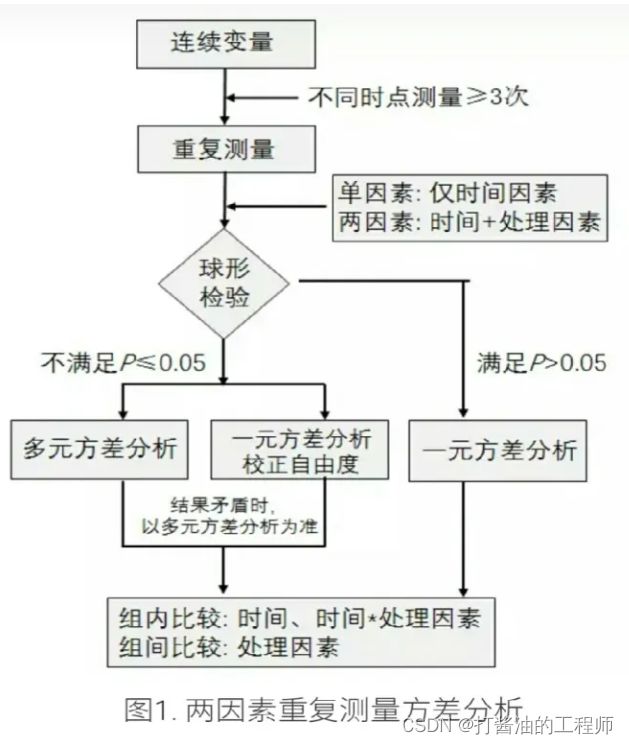
小白学完了重复测量方差分析课程,总结笔记,绘制如下图。
重复测量方差分析流程图
然后,向主任汇报了自己实验干预成果。
主任看后说:“小白,你运气真好呀,每次连续型变量都服从正态分布,如果不服从正态分布,你可知怎么办吗?”
小白说:“知道呀,有两种方法,一是原始数据转化为正态分布;二是采用秩和检验”
“那你会秩和检验吗?”
“还不太会,但我会好好学习,天天向上”
小白查了查下一讲内容:单样本秩和检验。
划重点
1、两因素重复测量设计可将研究对象随机分成两组,并对两组的指标重复测量多次。
2、两因素重复测量方差分析策略是:两个自变量(组间变量和组内变量),一个连续型因变量;组内变量重复测量多次,组间变量分成两组或多组;各组数据需满足正态性和球形度检验。
3、如果数据不满足正态分布,可采用Scheirer–Ray–Hare检验;如果不满足球形度检验,则采用多变量检验结果或者一元方差分析中校正结果。
4、两因素重复测量主要分析两自变量的主效应,两自变量的交互效应,以及简单效应。
5、如果两自变量之间不存在交互作用,则着重分析主效应;如果存在交互作用,着重分析交互效应和简单主效应。
6、对于多因素重复测混合设计(包括组间和组内变量)、多组内因素(没有组间变量)的重复测量设计,均可采用本文的统计策略。