OFDM同步--符号定时偏差STO

参考书籍：《MIMO-OFDM无线通信技术及MATLAB实现》 实验图基本都截取自该本书

一、什么是STO

  OFDM在接收时需要做FFT，需要在OFDM符号周期内获得对发射信号的精确采样，即在去CP之后我们需要找到OFDM的起始位，这样进行FFT运算时才能实现每一个符号位的对齐。时域$\delta$的STO同时会导致频域$2\pi k\delta /N$的相位偏移。

二、STO的影响

STO对符号采样的影响存在4种情况，假设多径延时拓展为${\tau }_{max}$

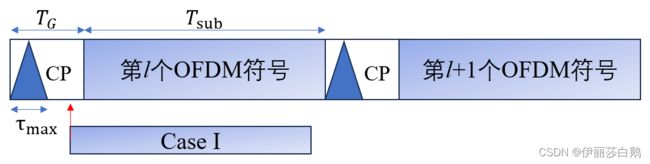
Case I

  估计的 OFDM 符号起始点与精确的定时一致，因此能够保持子载波频率分量之间的正交性。在这种情况下，可以完美地恢复 OFDM符号，而且没有任何干扰。

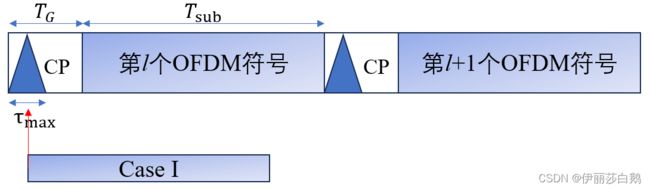
Case II

  估计的OFDM符号起始点在精确的定时点之前，但处在前一个OFDM符号信道响应的末端之后。在这种情况下，第I个符号与第I-1个符号不会重叠，即不存在由前一个符号引起的ISI。

  Case II 情况下子载波分量保持正交性但是恢复结果会出现固定相位偏移(对应星座图出现旋转，但并不散乱)，可以使用相位补偿器解决该问题。

Case III

  估计的OFDM符号起始点早于前一个OFDM 符号信道响应的末端，因此符号定时太早而无法避免ISI。这种情况下，子载波之间的正交性被(来自前一个符号的)ISI破坏，同时出现了ICI。

相位偏差严重，无法通过补偿进行矫正

Case IV

  估计的OFDM符号起始点滞后于精确的定时点。在这种情况下,在 FFT 间隔内，信号由当前的OFDM符号的一部分和下一个OFDM符号的一部分组成。

相位偏差严重，无法通过补偿进行矫正。

三、STO估计技术

  Case III 和 Case IV 已经无法仅使用补偿技术进行矫正了，因此需要估计出STO，使得接收机可以准确估计出OFDM符号的起始点。

3.1 时域STO估计

1. 基于CP的STO估计

  利用CP与数据的相似性去估计STO，利用间隔N个采样(N=OFDM符号采样长度)滑动窗口寻找接收数据最相似的情况，并将其定为OFDM的起始采样点。移动时不断变化的采样点时间，即 $\delta$ 便为STO的时域延时。
图为双滑动窗口的STO估计技术：

  当 W1 和 W 2中两个采样块之间相似度达到最大，估计出 $\delta$ 即可确定OFDM采样起始点。

W1与W2相似度计算方法

1. 差值估计
   直接计算搜索块的差值，尽管这种技术简单，但是当接收系统中存在 CFO 时其性能会下降。
   $$\hat{\delta }=\underset{\delta }{\mathrm{argmin}}\left\{\sum _{i=\delta }^{N_{\mathrm{G}-1+\delta }}\left|y_l[n+i]-y_l[n+N+i]\right|\right\}$$
2. 平方估计
   为了处理CFO, 通过最小化 W1 中采样块和 W2中采样块之差的平方来估计STO
   $$\hat{\delta }=\underset{\delta }{\mathrm{argmin}}\left\{\sum _{i=\delta }^{N_{\mathrm{G}}-1+\delta }{\left(\left|y_l[n+i]\right|-\mid y_l^{\ast }[n+N+i]\right)}^2\right\}$$
3. 相关性估计
   W1 和 W2 中两个采样块之间的相关性，即
   $$\hat{\delta }=\underset{\delta }{\mathrm{argmax}}\left\{\sum _{i=\delta }^{N_{\mathrm{G}}-1+\delta }\left|y_l[n+i]y_l{}^{\ast }[n+N+i]\right|\right\}$$
4. 最大似然估计
   最大化 W1 中采样块和 W2 中采样块之间的相关性。然而，当接收信号中存在 CFO 时的性能会下降。为了处理接收信号中的 CFO，通过最大化对数似然函数来估计STO。
   $${\hat{\delta }}_{\mathrm{ML}}=\underset{\delta }{\mathrm{argmax}}\left[\sum _{i=\delta }^{N_{\mathrm{G}-1+\delta }}2(1-\rho )\mathrm{Re}\left\{y_l[n+i]y_l^{\ast }[n+N+i]\right\}-\rho \sum _{i=\delta }^{N_{\mathrm{G}}-1+\delta }\left|y_l[n+i]-y_l[n+N+i]\right|\right]$$

2. 基于训练符号的STO技术

  通过发射训练符号，可以在接收机实现符号同步。与基于 CP 的方法相比，基于训练符号的方法存在因传输训练符号而带来的负荷问题，但是这种方法不受多径信道的影响 (我其实不太理解为什么不受多径信道影响，这也是书中提到的方法就放在这) 。在估计的过程中，可以使用两个相同的OFDM训练符号，也可以使用具有 (不同重复周期)重复结构的单个OFDM训练符号。

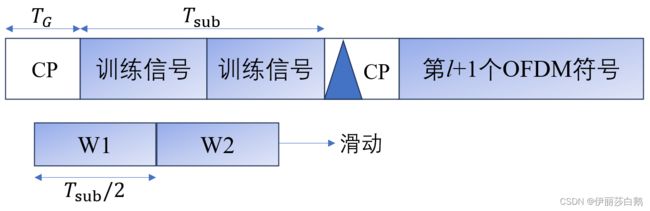
3.2 频域STO估计

  接收信号会因 STO 而产生相位旋转。相位旋转与子载波的频率成比例, 所以可以用频域接收信号中相邻子载波的相位差来估计 STO。频域 STO 估计技术通常会得到相当精确的估计值，所以能够用于精符号同步中，但是同样以为着更大的计算量。

3.2.1 训练符号

  一种利用相位旋转的影响进行 STO 估计的技术 。更具体地, 将训练符号的共轭 $X_l^{\ast }[k]$ 和存在 STO 的接收符号相乘，然后从中估计出 STO
$$\hat{\delta }=\underset{n}{\mathrm{argmax}}\left(y_l^{\mathrm{X}}[n]\right)$$其中$$\begin{array}{rl}{y}_l^{\mathrm{X}}[n]& =\mathrm{IFFT}\left\{Y_l[k]{\mathrm{e}}^{\mathrm{j}2\pi nk/N}{X}_l^{\ast }[k]\right\}\\ & =\frac{1}{N}\sum _{k=0}^{N-1}{Y}_l[k]{\mathrm{e}}^{\mathrm{j}2\pi \delta k/N}{X}_l^{\ast }[k]{\mathrm{e}}^{\mathrm{j}2\pi \delta k/N}\\ & =\frac{1}{N}\sum _{k=0}^{N-1}{H}_l[k]X_l[k]X_l^{\ast }[k]{\mathrm{e}}^{\mathrm{j}2\pi (\delta +n)k/N}\\ & =\frac{1}{N}\sum _{k=0}^{N-1}{H}_l[k]{\mathrm{e}}^{\mathrm{j}2\pi (\delta +n)k/N}\\ & =h_l[n+\delta ]\end{array}$$假设训练符号 $X[k]$ 的功率等于 1 , 即 $X[k]X_l^{\ast }[k]=|X[k]{|}^2=1$ 。

3.2.2 信道脉冲响应

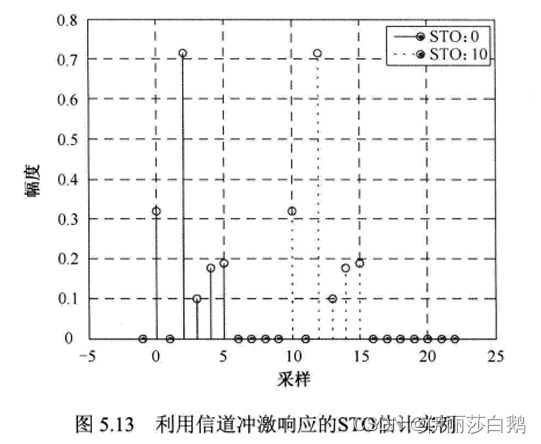
  利用信道脉冲响应进行 STO 估计的两个例子，其中一个0点采样，另一个10点采样。第一个信道脉冲响应从第 0个采样开始，用实线表示。第二个信道脉冲响应从第10个采样开始，用虚线表示。可以通过这种方法对 STO 进行正确的估计。

总结

  数字信号的同步一直都是数字信号处理中很关键的步骤，但在学习过程中我仅将同步视为必要步骤而不是复杂步骤。其实系统同步技术都很关键和复杂，经过同步的矫正才能保证系统的正确稳定。本文简要介绍了OFDM的STO同步，后续还会介绍OFDM另外一个重要的同步技术—>CFO同步。