【C语言】魔方阵的实现（最全）
魔方阵的实现（最全）
一、什么是魔方阵？
魔方矩阵，又称幻方，是具有相同的行数和列数，并在每行每列、对角线上的和都相等的矩阵。
N阶幻方，即将自然数1到
排成N行N列的方阵，使每行、每列及两条主对角线上的 N 个数的和相等，等于 
。
二、魔方阵的分类
对于魔方阵的构造，可分为一下三种类型：
- 奇数阶（N为奇数 [2n+1的形式] ）
- 单偶数阶（N为4的倍数 [4n的形式] ）
- 双偶数阶（N为其他偶数 [4n+2的形式] ）
三、魔方阵及代码实现
1、奇数阶魔方阵（n为奇数）
一般解法：
- 将1放在第一行中间一列
- 从2开始到
为止，每个数字的排放规律为：每一个数字排放的行比前一个数字的行数减1，每个数字排放的列比前一个数字的列数加1 - 行的特殊情况：如果前一个数字的行数为1，那么该数字排在第n行
- 列的特殊情况：如果前一个数字的列数为n，那么该数字排在第1列
- 其他情况：如果按照上面规律确定的位置上已经有数字，则把要排的数字放在上一个数字的下面。
下面为5阶魔方阵例子（各位读者可以根据以上解法思考）：
| 17 | 24 | 1 | 8 | 15 |
| 23 | 5 | 7 | 14 | 16 |
| 4 | 6 | 13 | 20 | 22 |
| 10 | 12 | 19 | 21 | 3 |
| 11 | 18 | 25 | 2 | 9 |
代码实现：
//奇数阶魔方阵
void odd_number(int n)
{
int i;
int row,line,row_0,line_0;//row为列坐标，line为行坐标，row_0记录行坐标，line_0记录列坐标
line=0;row=(n+1)/2-1;//初始化行、列坐标
a[line][row]=1;
for(i=2;i<=n*n;i++)
{
line_0=line;row_0=row;//记录上一次循环行、列坐标
if(line==0&&row==n-1)//第1行第n列的情况
{
line=n-1;//行坐标转到第n行
row=0;//列坐标转到第1行
}
else if(line==0)//第1行非第n列的情况
{
line=n-1;//行坐标转到第n行
row++;//列坐标+1
}
else if(row==n-1)//第n列非第1行的情况
{
row=0;//列坐标转到第1列
line--;//行坐标-1
}
else//普通情况
{
line--;//行坐标-1
row++;//列坐标+1
}
if(a[line][row]!=0)//判断该位置是否有数字
{
line=line_0+1;//（基于本次for循环开始的坐标）行坐标-1，转跳到下一行
row=row_0;//（基于本次for循环开始的坐标）列坐标不变
}
a[line][row]=i;//赋值
}
}2、单偶数阶魔方阵（n为偶数，且不能被4整除）
一般解法（以10阶魔方阵为例）：
- 首先把魔方阵均分为四个象限（形成四个奇数阶魔方阵），用奇数阶魔方阵填充的方法依次填充四个象限（顺序为A→D→B→C）。
A B C D 17 24 1 8 15 67 74 51 58 65 23 5 7 14 16 73 55 57 64 66 4 6 13 20 22 54 56 63 70 72 10 12 19 21 3 60 62 69 71 53 11 18 25 2 9 61 68 75 52 59 92 99 76 83 90 42 49 26 33 40 98 80 82 89 91 48 30 32 39 41 79 81 88 95 97 29 31 38 45 47 85 87 94 96 78 35 37 44 46 28 86 93 100 77 84 36 43 50 27 34 - 对于A象限的中间行，从中间格开始，自左至右标出k格；对于A象限的其他行，标出最左边k格（其中，k满足表达式n=4k+2）。
17 24 1 8 15 67 74 51 58 65 23 5 7 14 16 73 55 57 64 66 4 6 13 20 22 54 56 63 70 72 10 12 19 21 3 60 62 69 71 53 11 18 25 2 9 61 68 75 52 59 92 99 76 83 90 42 49 26 33 40 98 80 82 89 91 48 30 32 39 41 79 81 88 95 97 29 31 38 45 47 85 87 94 96 78 35 37 44 46 28 86 93 100 77 84 36 43 50 27 34 - 将A象限标出的数字与C象限中对应位置上的数互换位置。
92 99 1 8 15 67 74 51 58 65 98 80 7 14 16 73 55 57 64 66 4 6 88 95 22 54 56 63 70 72 85 87 19 21 3 60 62 69 71 53 86 93 25 2 9 61 68 75 52 59 17 24 76 83 90 42 49 26 33 40 23 5 82 89 91 48 30 32 39 41 79 81 13 20 97 29 31 38 45 47 10 12 94 96 78 35 37 44 46 28 11 18 100 77 84 36 43 50 27 34 - 对于B象限的所有行的中格，自左向右标出k-1格，并将其与D象限中对应位置的数字交换。
92 99 1 8 15 67 74 51 58 65 98 80 7 14 16 73 55 57 64 66 4 6 88 95 22 54 56 63 70 72 85 87 19 21 3 60 62 69 71 53 86 93 25 2 9 61 68 75 52 59 17 24 76 83 90 42 49 26 33 40 23 5 82 89 91 48 30 32 39 41 79 81 13 20 97 29 31 38 45 47 10 12 94 96 78 35 37 44 46 28 11 18 100 77 84 36 43 50 27 34 92 99 1 8 15 67 74 26 58 65 98 80 7 14 16 73 55 32 64 66 4 6 88 95 22 54 56 38 70 72 85 87 19 21 3 60 62 44 71 53 86 93 25 2 9 61 68 50 52 59 17 24 76 83 90 42 49 51 33 40 23 5 82 89 91 48 30 57 39 41 79 81 13 20 97 29 31 63 45 47 10 12 94 96 78 35 37 69 46 28 11 18 100 77 84 36 43 75 27 34
代码实现：
void single_even_number(int n)
{
int i,j;
int k,line,row,line_0,row_0;//k是与n相关的参数，line为行坐标，row为列坐标,line_0记录行坐标，row_0记录列坐标
k=(n-2)/4;
//A象限
line=0;row=k;//初始化A象限行列坐标
a[line][row]=1;
for(i=2;i<=(2*k+1)*(2*k+1);i++)//A象限的数字范围为1~(2*k+1)*(2*k+1)
{
line_0=line;row_0=row;//记录该次循环的初始行列坐标
if(line==0&&row==2*k)//第0行第2*k列的情况
{
line=2*k;//行坐标转为2*k
row=0;//列坐标转为0
}
else if(line==0)//第0行非第2*k列的情况
{
line=2*k;//行坐标转为2*k
row++;//列坐标+1
}
else if(row==2*k)//第2*k列非第0行的情况
{
row=0;//列坐标转为0
line--;//行坐标-1
}
else//普通情况
{
line--;//行坐标-1
row++;//列坐标+1
}
if(a[line][row]!=0)//判断是否遇到该位置有数字的情况
{
line=line_0+1;
row=row_0;
}
a[line][row]=i;//赋值
}
//D象限
line=2*k+1;row=3*k+1;//初始化D象限行列坐标
a[2*k+1][3*k+1]=(2*k+1)*(2*k+1)+1;
for(i=(2*k+1)*(2*k+1)+2;i<=2*(2*k+1)*(2*k+1);i++)//D象限数字范围(2*k+1)*(2*k+1)+1~2*(2*k+1)*(2*k+1)
{
line_0=line;row_0=row;//记录该次循环的初始行列坐标
if((line==2*k+1)&&(row==4*k+1))//第(2*k+1)行第(4*k+1)列的情况
{
line=4*k+1;//行坐标转为4*k+1
row=2*k+1;//列坐标转为2*k+1
}
else if(line==2*k+1)//第(2*k+1)行非第(4*k+1)列的情况
{
line=4*k+1;//行坐标转为4*k+1
row++;//列坐标+1
}
else if(row==4*k+1)//第(4*k+1)列非第(2*k+1)行的情况
{
row=2*k+1;//列坐标转为2*k+1
line--;//行坐标-1
}
else//普通情况
{
line--;//行坐标-1
row++;//列坐标+1
}
if(a[line][row]!=0)//判断是否遇到该位置有数字的情况
{
line=line_0+1;
row=row_0;
}
a[line][row]=i;//赋值
}
//B象限
line=0;row=3*k+1;//初始化B象限行列坐标
a[line][row]=2*(2*k+1)*(2*k+1)+1;
for(i=2*(2*k+1)*(2*k+1)+2;i<=3*(2*k+1)*(2*k+1);i++)//B象限数字范围2*(2*k+1)*(2*k+1)+1~3*(2*k+1)*(2*k+1)
{
line_0=line;row_0=row;//记录该次循环的初始行列坐标
if((line==0)&&(row==4*k+1))//第0行第(4*k+1)列的情况
{
line=2*k;//行坐标转为2*k
row=2*k+1;//列坐标转为2*k+1
}
else if(line==0)//第0行非第(4*k+1)列的情况
{
line=2*k;//行坐标转为2*k
row++;//列坐标+1
}
else if(row==4*k+1)//第(4*k+1)列非第0行的情况
{
row=2*k+1;//列坐标转为2*k+1
line--;//行坐标-1
}
else//普通情况
{
line--;//行坐标-1
row++;//列坐标+1
}
if(a[line][row]!=0)//判断是否遇到该位置有数字的情况
{
line=line_0+1;
row=row_0;
}
a[line][row]=i;//赋值
}
//C象限
line=2*k+1;row=k;//初始化C象限行列坐标
a[line][row]=3*(2*k+1)*(2*k+1)+1;
for(i=3*(2*k+1)*(2*k+1)+2;i<=4*(2*k+1)*(2*k+1);i++)//C象限数字范围3*(2*k+1)*(2*k+1)+1~4*(2*k+1)*(2*k+1)
{
line_0=line;row_0=row;//记录该次循环的初始行列坐标
if((line==2*k+1)&&(row==2*k))//第(2*k+1)行第2*k列的情况
{
line=4*k+1;//行坐标转为4*k+1
row=0;//列坐标转为0
}
else if(line==2*k+1)//第(2*k+1)行非第2*k列的情况
{
line=4*k+1;//行坐标转为4*k+1
row++;//列坐标+1
}
else if(row==2*k)//第2*k列非第(2*k+1)行的情况
{
row=0;//列坐标转为0
line--;//行坐标-1
}
else//普通情况
{
line--;//行坐标-1
row++;//列坐标+1
}
if(a[line][row]!=0)//判断是否遇到该位置有数字的情况
{
line=line_0+1;
row=row_0;
}
a[line][row]=i;//赋值
}
//换A、C象限相关数字的位置
for(i=0;i<2*k+1;i++)//对于A、C象限
{
int j_0,f=0;//j_0记录循环次数，f=0为标志位
for(j=0,j_0=0;j_0=2)
for(i=0;i 3、双偶数阶魔方阵（n为偶数，且能被4整除）
一般规律：
- 用横线和竖线将n阶魔方阵均分为m个
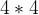的小魔方阵。 - 将
个数从小到大，从左到右，从上到下，依次填入方阵中，遇到4*4的小方阵的对角线不填（注：此位置不填的数不作为下一个位置填的数） - 将个数从小到大，从右到左，从下到上，依次填入方阵4*4的小方阵的对角线上，其他位置不填（注：此位置不填的数不作为下一个位置填的数）
- 将2、3两步得到的魔方阵合并为一个魔方阵，双偶数阶魔方阵排列完成。
| 64 | 2 | 3 | 61 | 60 | 6 | 7 | 57 |
| 9 | 55 | 54 | 12 | 13 | 51 | 50 | 16 |
| 17 | 47 | 46 | 20 | 21 | 43 | 42 | 24 |
| 40 | 26 | 27 | 37 | 36 | 30 | 31 | 33 |
| 32 | 34 | 35 | 29 | 28 | 38 | 39 | 25 |
| 41 | 23 | 22 | 44 | 45 | 19 | 18 | 48 |
| 49 | 15 | 14 | 52 | 53 | 11 | 10 | 56 |
| 8 | 58 | 59 | 5 | 4 | 62 | 63 | 1 |
解决双偶数阶魔方阵的关键是要准确计算对角线。
从左上到右下的对角线满足 line % 4 == row % 4
从右上到左下的对角线满足 ( line + row ) % 4 == 3
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | 0 | 3 | 4 | 7 | ||||
| 1 | 2 | 3 | 6 | 7 | ||||
| 2 | 3 | 4 | 7 | 8 | ||||
| 3 | 3 | 6 | 7 | 10 | ||||
| 4 | 4 | 7 | 8 | 11 | ||||
| 5 | 6 | 7 | 10 | 11 | ||||
| 6 | 7 | 8 | 11 | 12 | ||||
| 7 | 7 | 10 | 11 | 14 |
代码实现：
void double_even_number(int n)
{
int line,row;
int t_1=1,t_2=n*n;//t_1为正向，t_2为逆向
for(line=0;line主函数如下：
#include
#include
int a[100][100]={0};//将数组a中所有元素赋值为0
int main()
{
int n,i,j;
void odd_number(int n);
void single_even_number(int n);
void double_even_number(int n);
printf("请输入“魔方阵 ”的参数n=");
scanf("%d",&n);
if(n%2==1)
odd_number(n);
else if(n%4==2)
single_even_number(n);
else if(n%4==0)
double_even_number(n);
printf("该“魔方阵 ”如下:\n");
for(i=0;i