小学生都能看懂的三种进制之间的转换
超级简单的方法教你二进制、十进制、八进制、十六进制之间的相互转化
提示:进制转换是人们利用符号来计数的方法。进制转换由一组数码符号和两个基本因素“基数”与“位权”构成。基数是指,进位计数制中所采用的数码(数制中用来表示“量”的符号)的个数。位权是指,进位制中每一固定位置对应的单位值。
文章目录
-
- 超级简单的方法教你二进制、十进制、八进制、十六进制之间的相互转化
- 一、二进制与十进制的互转
-
- 1.1二进制转十进制
- 1.2十进制转二进制
- 二、八进制与二进制的互换
-
- 2.1 二进制转八进制
- 2.2八进制转二进制
- 三、十六进制与二进制互化
-
- 3.1 二进制转十六进制
- 3.2 十六进制转二进制
- 四、十进制转八进制、八进制转十进制、十六进制转八进制、八进制转十六进制
提示:这是本人总结的方法
一、二进制与十进制的互转
说明:
1)所谓二进制数,就是由0,1两个数排列组合成的数,其运算规则就是逢二进一。例如:
二进制数中:1+1=10
2)十进制就是我们从小在学校所接触的5+5=10的逢十进一的运算法则
1.1二进制转十进制
首先以我们的十进制为切入点:例如1432(十进制)
可以这样表示:

二进制同理:二进制数从左到右用2的幂次方表示十进制数
例如:10010(二进制数)可以用如下方法表示
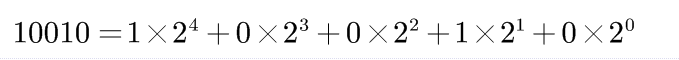
然后计算出最终结果就是:18(十进制数)
1.2十进制转二进制
最简单的方法是:列出从2的0次幂一直到2的7次幂(如果十进制的数够大,可以一直列到2的n次幂),然后把十进制数标在对应的位置。
例如:56转换成二进制
1)找到与56最近且小于56的数,首先这个数是32,所以在下面标1。56-32=24
2) 再找到与24最近且小于24的数,该数为16,所以在下面标1,以此类推
56=32+16+8 ( 其余位数不占位的用零填充)
所以最终转换成二进制就是:111000
二、八进制与二进制的互换
八进制
顾名思义:以8为单位的运算进制,采用0,1,2,3,4,5,6,7八个数字,逢八进1,满8进1。
2.1 二进制转八进制
例如
把01010转化成八进制
| 二进制 | 八进制 |
|---|---|
| 01010 | 12 |
在二进制转八进制中,我们采取二进制的三位去化八进制的一位。具体步骤和方法如下:
step1:把二进制数从右往左,每三位划一组,不足三位的用零补充。
step2 把划分为的两组的数字分别用上面二进制化十进制的方式化成十进制数。
step3把化成的十进制数按照顺序组合在一起就是所得的八进制数

PS:如果有小伙伴对二进制转十进制不是太熟悉,可以参考下面的对照表
| 二进制 | 十进制 |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
2.2八进制转二进制
八进制转二进制只需要按照上面2.1的步骤反推算就可以了
step1 把八进制的每一个数作为单独的数字进行转化
step1 八进制的一位数转化为三位的二进制数
step3把每组三位数按照顺序组合在一起就是二进制数
PS:这里就不画图了,如果你看懂了八进制转二进制,也就会了。
三、十六进制与二进制互化
十六进制
一种逢16进1的进位制。一般用数字0到9和字母A到F表示,其中:A~F表示10-15,这些称作十六进制数字。
3.1 二进制转十六进制
例如
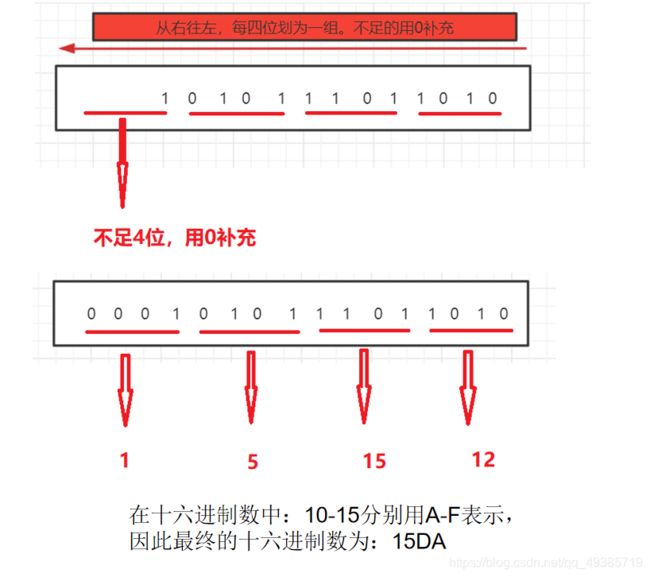
把二进制数1010111011010 化成十六进制数
| 二进制 | 八进制 |
|---|---|
| 1010111011010 | 15DA |
二进制转十六的方式与二进制转八进制类似。只不过十六进制转二进制是采用二进制的每四位去化十六进制的每一位。
步骤与八进制化二进制相同。只不过10-15是A-F表示
step1:把二进制数从右往左,每四位划一组,不足四位的用零补充。
step2 把划分的每组的数字分别用上面二进制化十进制的方式化成十进制数。
step3把化成的十进制数按照顺序组合在一起就是所得的十六进制数
PS:如果有小伙伴对二进制转十进制不是太熟悉,可以参考下面的对照表
| 二进制 | 十进制 |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 01001 | 9 |
| 1010 | A(10) |
| 1011 | B(11) |
| 1100 | C(12) |
| 1101 | D(13) |
| 1110 | E(14) |
| 1111 | F(15) |
3.2 十六进制转二进制
同理八进制转二进制。也是逆着推算。
step1 把十六进制的每一个数作为单独的数字进行转化
step1 十六进制的一位数转化为四位的二进制数
step3把每组四位数按照顺序组合在一起就是二进制数
PS:这里就不画图了,如果你看懂了十六进制转二进制,也就会了。
四、十进制转八进制、八进制转十进制、十六进制转八进制、八进制转十六进制
这些转化的话,都是以二进制数作为中间介质。再进行互化。