【C语言初阶（11）】递归练习题

1. 打印一个整型的每一位

题目内容

• 接受一个整型值（无符号），按照顺序打印它的每一位。
  • 例如：输入 1234，输出 1 2 3 4。

如何得到 1234 的每一位？

1. 如果想得到 1234 的最后一位的话，只需要 1234 %10 就可以得到 4，得到 4 之后将之打印出来；
2. 既然已经得到了 4，那么就不在需要它了，此时用 1234 / 10 = 123 就能去掉最后一位数；
3. 重复上面两个步骤，直到 1234 只剩个位数的时候停止循环即可。

• 此时已经了解了如何获取一个多位数上的每位数字，但是这个结果显然不是我们想要的正序打印，此时就该了解如何使用递归来求解了。

递归实现的解题思路

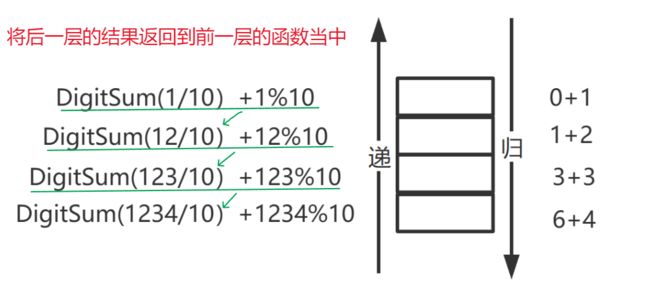
• 通过前面我们已经知道 1234 最好拿到的是最后一位的 4，然而我们想要正序打印就必须先拿到第一位的 1，然后将之打印出来。
• 也就是说，我们应该通过递归不停地 n / 10，直到 n 只剩第一位的 1 时结束递进开始回归。回归的过程中就可以很好的将 1234 的每一位打印出来了。

代码实现

#include 
void print(unsigned int n)
{
	if (n > 9)// n>9 说明 n 还有的拆
	{
		print(n / 10);
	}
	printf("%u ", n % 10);//递推结束开始回归时这条语句才能被执行
}
int main()
{
	unsigned int num = 1234;
	print(num);
	return 0;
}

代码分析

看到递归了吗

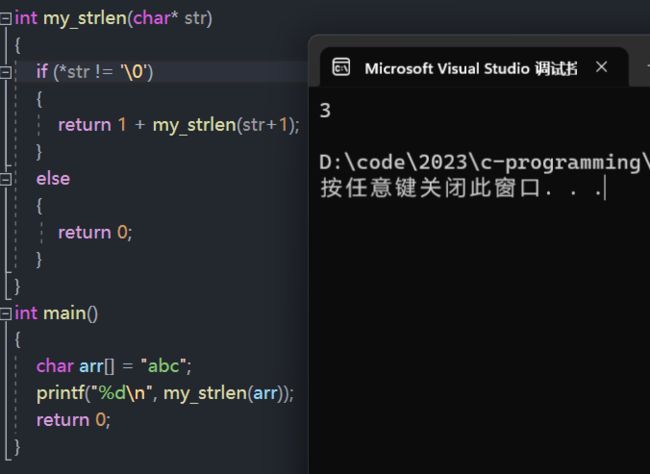
2. 求字符串长度

题目内容

• 编写函数不允许创建临时变量，求字符串的长度。
• 一般而言，像这种求字符串长度的题，创建临时变量来做的话都蛮简单的。

• 但是不允许创建临时变量就显得很变态了，此时只能使用递归来写了。

解题思路

• 数组在传参的时候传过去的是数组首元素的地址，如果这个地址指向的第一个字符不是 \0 那串的长度就至少为 1，就可以进行递归；
• 每次递归让地址 +1 指向下一个字符，并且数量 +1 ，直到遇到 \0 递归结束，开始返回。
• 在回归过程中将遇到的所有 1 全部加起来就是串的长度。

代码实现

#include 
int my_strlen(char* str)
{
	//如果第一个字符不等于 \0，那它的长度至少是1
	if (*str != '\0')
	{
		return 1 + my_strlen(str+1);
	}
	else
	{
		return 0;
	}
}
int main()
{
	char arr[] = "abc";
	printf("%d\n", my_strlen(arr));
	return 0;
}

代码分析

my_strlen(“abc”)
1 + my_strlen(“bc”)
1+1+my_strlen(“c”)
1+1+1+my_strlen(“”)

图解1

3. 求 n 的阶乘

阶乘公式

• 有了公式的话就很好解决了，递归套用公式就行了。

代码实现

#include 
int fac(int n)
{
	if (n > 1)
	{
		return n * fac(n - 1);
	}
	else
	{
		return 1;// 0 和 1 的阶乘都是 1
	}
}
int main()
{
	int n;
	scanf("%d", &n);//以 n =  5 做例子
	printf("%d\n", fac(n));
	return 0;
}

代码分析

4. 求第 n 个斐波那契数

斐波那契数

• 斐波那契数列指的是这样一个数列：
  • 1，1，2，3，5，8，13，21，34，55，89，144，233，377，610，987，1597，2584，4181，6765，10946，17711……
• 它们的规律是：这个数列从第 3 项开始，每一项都等于前两项之和。

4.1 递归算法

斐波那契数公式

• 通过求阶乘那节可以发现，在有了函数公式的情况下，递归写起来基本就是有手就行了；
• 斐波那契数当然也有自己的公式：

代码实现

#include 
int Fib(int n)
{
	if (n > 2) //从第三位才开始求斐波那契数
	{
		return Fib(n - 1) + Fib(n - 2);
		//公式：fib(n) = fib(n-1) + fib(n-2)
	}
	else
	{
		return 1; // 前两个斐波那契数都是 1
	}
}
int main()
{
	int n;
	scanf("%d", &n);
	printf("%d\n", Fib(n));
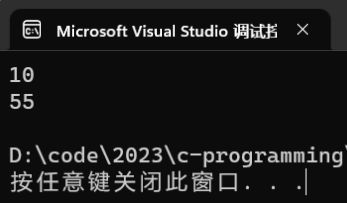
	return 0;
}

• 在使用 fib 这个函数的时候如果我们要计算第 50 个斐波那契数字的时候特别耗费时间。
  • 博主的电脑在求第 50 个斐波那契数的时候用了有足足两分钟。

不推荐使用递归求斐波那契数

• 在使用递归求解斐波那契数的时候，会出现大量重复性的计算，导致程序执行效率很底。
• 如下图：想求第 6 个斐波那契数就得先求出第 5 个以及第 4 个斐波那契数；
• 想求出第 5 个斐波那契数就又要先求 第 4 个以及第 3 个斐波那契数，这才第二步就开始出现重复运算了。

• 来看看在求第 40 个斐波那契数的过程中，重复求了第 3 个斐波那契数多少次：

#include 
int count_fib_3 = 0;
int Fib(int n)
{
	//记录在运算某个数的过程中求了多少次第 3 个斐波那契数
	if(3==n)
	{	
		count_fib_3++;
	}
	if (n > 2)
	{
		return Fib(n - 1) + Fib(n - 2);
	}
	else
	{
		return 1;
	}
}
int main()
{
	int n;
	scanf("%d", &n);
	printf("%d\n", Fib(n));
	printf("%d\n", count_fib_3);
	return 0;
}

可以看到，光是第 3 个斐波那契数就重复求了将近四千万次，那是相当的夸张。

4.2 非递归算法

• 为了解决用递归求斐波那契数出现的大量的重复计算现象，使用迭代求斐波那契数无疑是一个更好的选择。

迭代定义

• 迭代就是重复的意思；
• 循环是迭代，迭代不一定是循环。

解题思路

• 使用递归我们是从后往前算的，那么使用迭代我们就从前往后算。
• 使用三个变量来存储 第 1、2 个数以及前两数之和。
• 通过不断交换三个变量的值，从而在一条斐波那契数列上进行移动。

解题步骤

1. 先将变量 a 和 b 的值都赋成 1，然后执行 a + b = c ;
   • 从第 3 个数开始才去求斐波那契数，因为前两个斐波那契数都是 1。
2. 算好之后将 b 的值赋给 a，将 c 的值赋给 b，然后执行 a + b = c，产生新的变量 a b c，然后将 n 的值减 1；
3. 重复上面两个步骤，直到 n 的值等于 3 结束循环。

代码实现

#include 
int Fib(int n)
{
	int a = 1, b = 1, c = 1;
	while(n >= 3)
	{
		c = a + b;
		a = b;
		b = c;
		n--;
	}
	return c;
}
int main()
{
	int n;
	scanf("%d", &n);
	printf("%d\n", Fib(n));
	return 0;
}

• 现在算第 50 个斐波那契数虽然结果是错的，但是效率提升上来了。

• 使用了迭代的方法计算斐波那契数之后，需要重复计算的步骤就彻底被干掉了。

5. 字符串逆序

题目内容

• 编写一个函数 reverse_string(char* string)（递归实现）。
• 实现：将参数字符串中的字符反向排列，不是逆序打印。
• 要求：不能使用 C 库函数中的字符串操作函数。

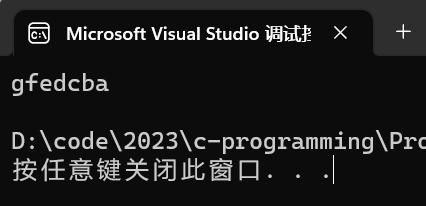
char str[] = "abcdef";
逆序之后数组的内容变成：fedcba

解题思路

整个问题可以分解成两个部分。

1. 调用 reverse 函数交换首尾两个字符。
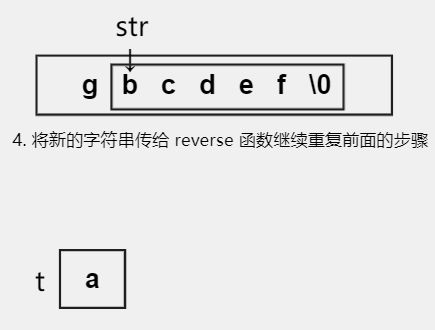
2. 将中间的所有字符作为一个新的字符串传给 reverse 函数进行逆序

• 重复以上两个部分就能够实现字符串的逆序。

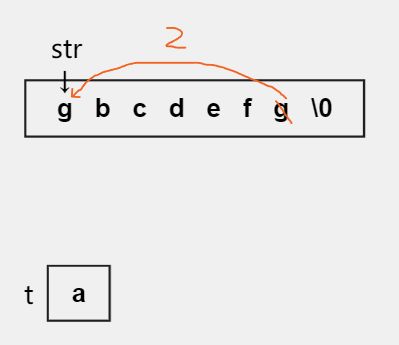
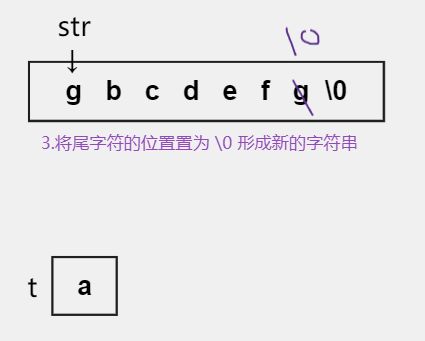
解题步骤

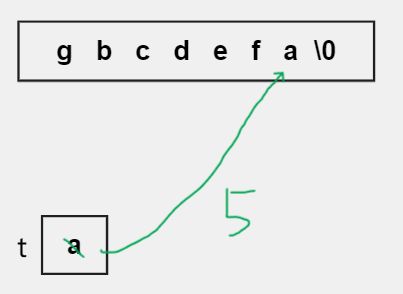
1. 创建一个临时变量 t 用来存放字符串的首字符。
2. 将尾字符放的值赋给首字符的位置。
3. 在尾字符的位置放置一个 \0 ，从而让中间的字符重新形成一个字符串。
4. 让指针+1指向下一个字符，将得到的新字符串继续传给 reverse 函数执行递归。
5. 最后将交给 t 保管的首字符赋到尾字符的位置，这样两个字符就交换完成了。

递归执行条件

• 看下中间还剩几个字符，当逆序到中间只剩一个字符的时候就不用继续递归了。
• 也就是说，当中间这个串的长度为 >= 2 时，才会执行递归。

代码实现

#include 

int my_strlen(char* str)
{
	int count = 0;
	while (*str != '\0')
	{
		count++;
		str++;
	}
	return count;
}

void reverse(char* str)
{
	int len = my_strlen(str);
	char t = *str;			//step1 
	*str = *(str + len - 1);//step2
	*(str + len - 1) = '\0';//step3

	//求的是中间这个串的长度，所以要+1
	if (my_strlen(str + 1) >= 2)
	{
		reverse(str + 1);	//step4
	}
	*(str + len - 1) = t;	//stpe5
}

int main()
{
	char str[] = "abcdefg";

	reverse(str);//字符串逆序
	printf("%s\n", str);

	return 0;
}

6. 计算一个数的每位之和

题目内容

• 写一个函数 DigitSum(n)，输入一个非负整数，返回组成它的数字之和。
• 例如：调用 DigitSum(1234)，则应该返回1+2+3+4，它的和为 10。
• 输入：1234，输出：10

解题思路

• 前面已经知道了如何将一个多位数的每一位拆下来，这题无非就是将拆下来的每一位加起来而已。

递归执行条件

• 当 n > 9 时说明还是两位数，这个数还有的拆。
• 当 n 是个位数时，这个数的每位之和就是它本身。

代码实现

#include 

unsigned int DigitSum(unsigned int n)
{
	if (n > 9)
	{
		return DigitSum(n / 10) + n % 10;
	}
	
}

int main()
{
	unsigned int n;
	scanf("%u", &n);
	printf("%u\n", DigitSum(n));

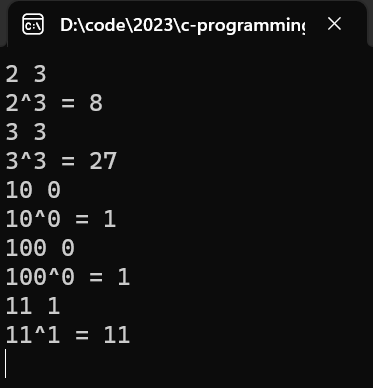
	return 0;
}

7. 递归实现 n 的 k 次方

题目内容

• 编写一个函数实现求 n 的 k 次方，使用递归来实现。

解题思路

• k 是几就让 n 乘多少次他自己，当 k 大于 0，时执行递归。
• 每次递归都让 k 的值 - 1，直到 k 等于 0 再结束递归。

代码实现

#include 

int my_pow(int n, int k)
{
	if (k > 0)
	{
		return n * my_pow(n, k - 1);
	}
}

int main()
{
	int n = 0;
	int k = 0;
	
	while (EOF != scanf("%d %d", &n, &k))
	{
		printf("%d^%d = %d\n", n, k, my_pow(n, k));
	}

	return 0;
}