Java 算法篇-深入了解二分查找法

博客主页： 小扳_-CSDN博客
❤感谢大家点赞收藏⭐评论✍  

 

目录

        1.0 二分查找法的说明

        2.0 二分查找实现的多种版本

        2.1 二分查找的基础版本

        2.2 二分查找的改动版本

        2.3 二分查找的平衡版本

        2.4 二分查找的官方版本

        3.0 二分查找的应用

---

        1.0 二分查找法的说明

        二分查找法（Binary Search）是一种在有序数组或有序列表中查找特定元素的搜索算法。其基本思想是将数组或列表分成两部分，取中间位置的元素进行比较，若该元素等于目标值，则查找成功；若该元素大于目标值，则在左半部分继续查找；若该元素小于目标值，则在右半部分继续查找。不断重复这个过程，直到找到目标值或查找范围缩小到只剩下一个元素为止。

        需要重点注意的是，使用二分查找的前提必须是数组是有序的或者列表是有序的。

        2.0 二分查找实现的多种版本

        基本来说可以分为基础版本和改动版本、平衡版、官方版本。

        2.1 二分查找的基础版本

        先来讲讲具体的实现吧，需要一个有序的数组 arr[] 或者有序列表，还有拿到需要查找的目标元素 int target。

        需要定义一下三种变量：

        第一种，int left ；一开始记录着是最左边的元素的索引，即为 0.

        第二种，int right；一开始记录着是最右边的元素的索引，即为 array.length - 1. 

        第三种，int mid；记录着是中间的元素的索引，即为（left + right）>>> 1;

        接着先要用 arr[mid] 的元素与 target 进行对比，这时候就会有三种情况，分别做不同的处理，假如 if(arr[mid] < target )，中间的元素小于目标元素时，要对 left 进行 left = mid + 1处理，假如 if(arr[mid] > target )，中间的元素大于目标元素时，要对 right 进行 right = mid - 1处理，假如 if(arr[mid] = target )，这时候就找到了目标元素了，直接返回 mid ，因此这是一个循环的过程，不断缩小范围来寻找目标元素，这一切都需要满足 left <= right 这个条件。

具体代码实现如下：

public class BinarySearch {
    public static void main(String[] args) {
        int[] arr = {1,3,5,7,9,11};
        int target = 3;
        System.out.println(search(arr, target));
    }
    public static int search(int[] arr, int target){
        int left = 0;
        int right = arr.length - 1;
        while (left <= right){
            int mid = (left + right) >>> 1;
            if (arr[mid] < target){
                left = mid + 1;
            } else if (target < arr[mid]) {
                right = mid - 1;
            }else {
                return mid;
            }
        }
        return -1;
    }
}

运行结果如下：

        目标元素3的索引为1，补充一下，若没有找到的话，这里定义返回为 -1 。

        2.2 二分查找的改动版本

        这个版本在基础版本的基础上进行了三点改动：

        第一点；int right；一开始记录着是最右边的元素的索引，即为 array.length 。

        注意，在基础版本中是需要减1的，而这里直接取元素个数，当然我们都知道这个会出现越界情况，所以才会有第二点改动 。

        第二点；这一切都需要满足 left < right 这个条件。

        这基础版本中循环条件是需要 <= 的条件，这里就不需要了，来分析一下为什么呢？

        原因就在第一点，在 right 索引下的元素是不可取的，重点在<不可取>，仔细品味一下，无论right 在之后的循环中得到的所有索引都是不可取到的元素。

        第三点；假如 if(arr[mid] > target )，中间的元素大于目标元素时，要对 right 进行 right = mid 处理。

具体代码实现如下：

public class NewBinarySearch {
    public static void main(String[] args) {
        int[] arr = {1,3,5,7,9,11};
        int target = 3;
        System.out.println(search(arr, target));
    }
    public static int search(int[] arr, int target) {
        int left = 0;
        int right = arr.length;
        while (left < right) {
            int mid = (left + right) >>> 1;
            if (arr[mid] < target) {
                left = mid + 1;
            } else if (target < arr[mid]) {
                right = mid;
            } else {
                return mid;
            }
        }
        return -1;
    }
}

运行结果如下：

         2.3 二分查找的平衡版本

        相对比与第一、两种，这个版本的效率会更高一点。这种版本的思路就是将范围不断缩小为1，然后获取 left 索引下的元素，来判断是否等于目标元素。

具体代码如下：

public class NewBinarySearch {
    public static void main(String[] args) {
        int[] arr = {1,3,5,7,9,11};
        int target = 3;
        System.out.println(search(arr, target));
    }
    public static int search (int[] arr, int target){
        int left = 0;
        int right = arr.length;
        while (1 < right - left){
            int mid = (left + right) >>> 1;
            if (target < arr[mid]){
                right = mid;
            } else  {
                left = mid;
            }
        }
        if (arr[left] == target){
            return left;
        }else {
            return -1;
        }

    }
}

运行结果如下：

        2.4 二分查找的官方版本

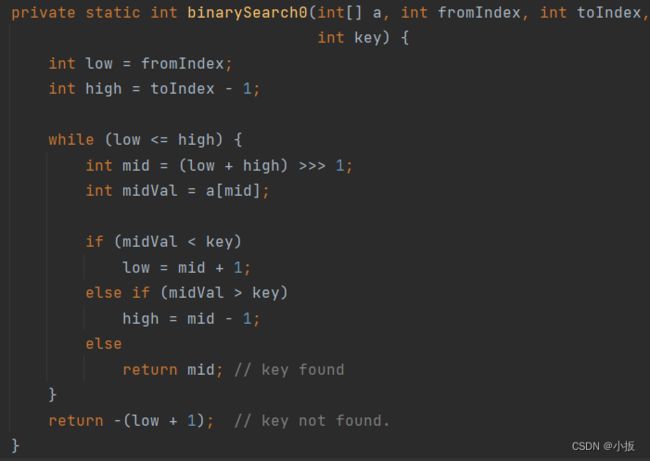
直接来看原代码：

        来分析一下，从总体来看，官方的二分查找的实现跟第一种的基本版本是大致相同的，有一点跟基础版本的不同的是，就是返回值。在基础版本中，如果找不到就返回 -1，而这里返回的是 -（low + 1），接下来具体讲解一下。

        第一点，low 代表的是插入点，这个值跟 left 的值是一样的。

        第二点，关于负数的说法，一般来说找不到的元素时，会返回负数。

具体代码的实现：

public class NewBinarySearch {

    public static void main(String[] args) {
        int[] arr = {1,3,5,7,9,11};
        int target = 2;
        System.out.println(search(arr, target));
    }
    public static int search(int[] arr, int target) {
        int left = 0;
        int right = arr.length - 1;
        while (left <= right) {
            int mid = (left + right) >>> 1;
            if (arr[mid] < target) {
                left = mid + 1;
            } else if (target < arr[mid]) {
                right = mid - 1;
            } else {
                return mid;
            }
        }
        return -(left + 1);
    }
}

运行结果如下：

        来算一下，我们知道 2 在数组中是不存在的，插入点为 1 ，则-（1+1）==  -2，验证了是符合的结果的。

 

        3.0 二分查找的应用

        给出下列数组 int[] arr {1,2,3,3,3,3,5,6,7} 要求返回目标元素3的起始位置与结束位置。

        实现的思路：先找起始位置，首先得先找到目标元素的索引，之后得往左边去找。找结束位置也是同理，首先得先找到目标元素的索引，之后得往右边去找。

代码如下：

public class NewBinarySearch {
    public static void main(String[] args) {
        int[] arr = {1,2,3,3,3,3,5,6,7};
        int target = 3;
        System.out.print(findLeft(arr, 3)+" ");
        System.out.println(findRight(arr, 3));
    }
    public static int findLeft(int[] arr,int target){
        int left = 0;
        int right = arr.length - 1;
        int sign = -1;
        while (left <= right){
            int mid = (left + right) >>> 1;

            if (arr[mid] < target){
                left = mid + 1;
            } else if (target < arr[mid]) {
                right = mid - 1;
            }else {
                sign = mid;
                right = mid - 1;
            }
        }
        return sign;
    }

    public static int findRight(int[] arr, int target){
        int left = 0;
        int right = arr.length - 1;
        int sign = -1;
        while (left <= right){
            int mid = (left + right) >>> 1;
            if (arr[mid] < target){
                left = mid + 1;
            } else if (target < arr[mid]) {
                right = mid - 1;
            }else {
                sign = mid;
                left = mid + 1;
            }
        }
        return sign;
    }
}

运行结果如下：