Day19 力扣二叉树 : 669. 修剪二叉搜索树 |108.将有序数组转换为二叉搜索树 | 538.把二叉搜索树转换为累加树 |二叉树总结
Day19 力扣二叉树 : 669. 修剪二叉搜索树 |108.将有序数组转换为二叉搜索树 | 538.把二叉搜索树转换为累加树
- 669. 修剪二叉搜索树
- 108.将有序数组转换为二叉搜索树
- 538.把二叉搜索树转换为累加树
- 二叉树总结:
-
- 二叉树的理论基础
- 二叉树的遍历方式
- 求二叉树的属性
- 二叉树的修改与构造
- 求二叉搜索树的属性
- 二叉树公共祖先问题
- 二叉搜索树的修改与构造
669. 修剪二叉搜索树
这道题目比较难,比 添加增加和删除节点难的多,建议先看视频理解。
题目链接/文章讲解:
https://programmercarl.com/0669.%E4%BF%AE%E5%89%AA%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91.html 视频讲解: https://www.bilibili.com/video/BV17P41177ud
第一印象:
这道题看起来就做不出来,删除一个节点后,仍然要保留他的子树部分,直接看一手题解。
看完题解的思路:
看完也是有些混乱,递归不仅出现在左右递归,还出现在root的逻辑里。
返回值:
因为是要遍历整棵树,做修改,其实不需要返回值也可以,我们也可以完成修剪(其实就是从二叉树中移除节点)的操作。
但是有返回值,更方便,可以通过递归函数的返回值来移除节点。这样的做法在二叉树:搜索树中的插入操作 (opens new window)和二叉树:搜索树中的删除操作 (opens new window)中大家已经了解过了。
终止条件:
遇到空节点返回null
单层递归逻辑:
对于当前root节点,如果<左边界,应该将修剪好的右子树返回,如果>右边界,应该将修剪好的左子树返回。
然后左右递归root的左右节点,将下一层处理完左子树的结果赋给root->left,处理完右子树的结果赋给root->right。
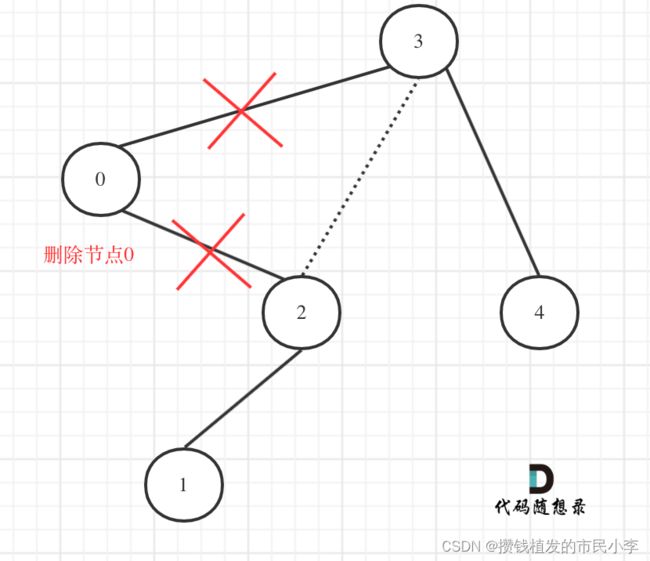
而我感觉奇怪的就是,对root的左子树便利了两次,一次是因为root的val不符合,一次是对root的左递归。这个问题在代码随想录里得到了解答:
就是处理节点0的时候return了节点2,然后在节点3的左递归时接住了这个节点2.
实现时的困难:
思路清楚之后实现起来不困难,但是思路也没完全清楚,不是独立思考能出来的。
感悟:
对于递归的返回值还是困惑一些,但是更理解了这个四处递归的原因,理解了一些 接住 的思想。
代码:
class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
if (root == null) return null;
//中 如果这个节点是被删除的
if (root.val < low) {
TreeNode right = trimBST(root.right, low, high);
return right;
}
if (root.val > high) {
TreeNode left = trimBST(root.left, low, high);
return left;
}
//如果这个节点满足要求,将修剪好的左右子树的头节点弄过来
//左
root.left = trimBST(root.left, low, high);
//右
root.right = trimBST(root.right, low, high);
return root;
}
}
108.将有序数组转换为二叉搜索树
本题就简单一些,可以尝试先自己做做。
https://programmercarl.com/0108.%E5%B0%86%E6%9C%89%E5%BA%8F%E6%95%B0%E7%BB%84%E8%BD%AC%E6%8D%A2%E4%B8%BA%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91.html
视频讲解:https://www.bilibili.com/video/BV1uR4y1X7qL
第一印象:
我先自己试试,我隐约记得这个需要LR LL那种旋转来着。二叉搜索树变成有序数组是中序遍历,那我觉得构建二叉搜索树应该也是中序遍历。
完了,没思路,我想不出是怎么递归的。
看完题解的思路:
本题其实要比二叉树:构造二叉树登场! (opens new window) 和 二叉树:构造一棵最大的二叉树 (opens new
window)简单一些,因为有序数组构造二叉搜索树,寻找分割点就比较容易了。分割点就是数组中间位置的节点。
确实,之前根据后序中序来构造二叉树,找分割点什么的还是挺麻烦的,参数很容易弄错,
他们都是构造二叉树一类的题。那我就会了啊
再就是这道题有一个数组长度为偶数的时候,有两个中间节点,选哪一个作为分割点呢?
直接给出题解里的答案,考研的时候确实遇到过这个事情。
实现中的困难:
递归函数的返回值问题还是有些想当然,不熟练。
感悟:
学会了构造二叉树一类问题,印象更深了。
代码:
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
TreeNode root = toBST(nums, 0, nums.length);
return root;
}
private TreeNode toBST(int[] nums, int left, int right) {
//左闭右开 [1,1)不合法
if (left >= right) return null;
int mid = (left + right) / 2;
TreeNode root = new TreeNode(nums[mid]);
root.left = toBST(nums, left, mid);
root.right = toBST(nums, mid + 1, right);
return root;
}
}
538.把二叉搜索树转换为累加树
本题也不难,在 求二叉搜索树的最小绝对差 和 众数 那两道题目 都讲过了 双指针法,思路是一样的。
https://programmercarl.com/0538.%E6%8A%8A%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E8%BD%AC%E6%8D%A2%E4%B8%BA%E7%B4%AF%E5%8A%A0%E6%A0%91.html
视频讲解:https://www.bilibili.com/video/BV1d44y1f7wP
第一印象:
双指针我觉得会,但是这道题他是右根左这样的顺序去加,不是正常的中序。
先看一下题解吧,双指针细想也有些遗忘了。
不看了 操,我自己做。
做出来了,我牛逼,右根左去中序遍历没毛病噢。我是双指针的神
再看一遍视频和题解加深一下吧。
看完题解的思路:
我有点写麻烦了,这道题不太需要pre指针,可以直接用sum累加赋值就行
但我觉得写明pre指针挺好的,慢慢体会吧
实现的困难:
没有
感悟:
无敌啦
代码:
我的
class Solution {
TreeNode pre = null;
int sum = 0;
public TreeNode convertBST(TreeNode root) {
if (root == null) return null;
TreeNode right = convertBST(root.right);
root.right = right;
if (pre == null) {
sum += root.val;
} else {
sum += root.val;
root.val = sum;
}
pre = root;
TreeNode left = convertBST(root.left);
root.left = left;
return root;
}
}
题解的:
class Solution {
int sum;
public TreeNode convertBST(TreeNode root) {
sum = 0;
convertBST1(root);
return root;
}
// 按右中左顺序遍历,累加即可
public void convertBST1(TreeNode root) {
if (root == null) {
return;
}
convertBST1(root.right);
sum += root.val;
root.val = sum;
convertBST1(root.left);
}
}
二叉树总结:
- 首先一定是二叉树的基本概念、二叉树类的写法
- 每一道题都可以用递归去做,递归三部曲返回值?参数?单层递归逻辑?
有一种确定返回值的方法,我还没有掌握
参数一般比较简单
单层递归逻辑是具体的题目了,也是较难。 - 至于迭代法,一刷我还没有掌握,在层序遍历那里经常用
- 有递归就有回溯,我理解回溯的过程,但是我还不能看到一类题就想到回溯,也不能看出隐藏的回溯,但是没关系,下一章节就是回溯,我体会一下。
- 题的类型:直接来自代码随想录的总结。
二叉树的理论基础
关于二叉树,你该了解这些! (opens new window):二叉树的种类、存储方式、遍历方式、定义方式
二叉树的遍历方式
深度优先遍历
二叉树:前中后序递归法 (opens new window):递归三部曲初次亮相
二叉树:前中后序迭代法(一) (opens new window):通过栈模拟递归
二叉树:前中后序迭代法(二)统一风格 (opens new window)
广度优先遍历
二叉树的层序遍历 (opens new window):通过队列模拟
求二叉树的属性
二叉树:是否对称 (opens new window)
递归:后序,比较的是根节点的左子树与右子树是不是相互翻转
迭代:使用队列/栈将两个节点顺序放入容器中进行比较
二叉树:求最大深度 (opens new window)
递归:后序,求根节点最大高度就是最大深度,通过递归函数的返回值做计算树的高度
迭代:层序遍历
二叉树:求最小深度 (opens new window)
递归:后序,求根节点最小高度就是最小深度,注意最小深度的定义
迭代:层序遍历
二叉树:求有多少个节点 (opens new window)
递归:后序,通过递归函数的返回值计算节点数量
迭代:层序遍历
二叉树:是否平衡 (opens new window)
递归:后序,注意后序求高度和前序求深度,递归过程判断高度差
迭代:效率很低,不推荐
二叉树:找所有路径 (opens new window)
递归:前序,方便让父节点指向子节点,涉及回溯处理根节点到叶子的所有路径
迭代:一个栈模拟递归,一个栈来存放对应的遍历路径
二叉树:递归中如何隐藏着回溯 (opens new window)
详解二叉树:找所有路径 (opens new window)中递归如何隐藏着回溯
二叉树:求左叶子之和 (opens new window)
递归:后序,必须三层约束条件,才能判断是否是左叶子。
迭代:直接模拟后序遍历
二叉树:求左下角的值 (opens new window)
递归:顺序无所谓,优先左孩子搜索,同时找深度最大的叶子节点。
迭代:层序遍历找最后一行最左边
二叉树:求路径总和 (opens new window)
递归:顺序无所谓,递归函数返回值为bool类型是为了搜索一条边,没有返回值是搜索整棵树。
迭代:栈里元素不仅要记录节点指针,还要记录从头结点到该节点的路径数值总和
二叉树的修改与构造
翻转二叉树 (opens new window)
递归:前序,交换左右孩子
迭代:直接模拟前序遍历
构造二叉树 (opens new window)
递归:前序,重点在于找分割点,分左右区间构造
迭代:比较复杂,意义不大
构造最大的二叉树 (opens new window)
递归:前序,分割点为数组最大值,分左右区间构造
迭代:比较复杂,意义不大
合并两个二叉树 (opens new window)
递归:前序,同时操作两个树的节点,注意合并的规则
迭代:使用队列,类似层序遍历
求二叉搜索树的属性
二叉搜索树中的搜索 (opens new window)
递归:二叉搜索树的递归是有方向的
迭代:因为有方向,所以迭代法很简单
是不是二叉搜索树 (opens new window)
递归:中序,相当于变成了判断一个序列是不是递增的
迭代:模拟中序,逻辑相同
求二叉搜索树的最小绝对差 (opens new window)
递归:中序,双指针操作
迭代:模拟中序,逻辑相同
求二叉搜索树的众数 (opens new window)
递归:中序,清空结果集的技巧,遍历一遍便可求众数集合
二叉搜索树转成累加树 (opens new window)
递归:中序,双指针操作累加
迭代:模拟中序,逻辑相同
二叉树公共祖先问题
二叉树的公共祖先问题 (opens new window)
递归:后序,回溯,找到左子树出现目标值,右子树节点目标值的节点。
迭代:不适合模拟回溯
二叉搜索树的公共祖先问题 (opens new window)
递归:顺序无所谓,如果节点的数值在目标区间就是最近公共祖先
迭代:按序遍历
二叉搜索树的修改与构造
二叉搜索树中的插入操作 (opens new window)
递归:顺序无所谓,通过递归函数返回值添加节点
迭代:按序遍历,需要记录插入父节点,这样才能做插入操作
二叉搜索树中的删除操作 (opens new window)
递归:前序,想清楚删除非叶子节点的情况
迭代:有序遍历,较复杂
修剪二叉搜索树 (opens new window)
递归:前序,通过递归函数返回值删除节点
迭代:有序遍历,较复杂
构造二叉搜索树 (opens new window)
递归:前序,数组中间节点分割
迭代:较复杂,通过三个队列来模拟
- 卡哥给的一些总结:
-
涉及到二叉树的构造,无论普通二叉树还是二叉搜索树一定前序,都是先构造中节点。
-
求普通二叉树的属性,一般是后序,一般要通过递归函数的返回值做计算。
-
求二叉搜索树的属性,一定是中序了,要不白瞎了有序性了。
注意在普通二叉树的属性中,我用的是一般为后序,例如单纯求深度就用前序,二叉树:找所有路径 (opens new window)也用了前序,这是为了方便让父节点指向子节点。
我对第二条还没有什么体会。
先总结到这吧,有机会的话对每一章节都单独发个文章总结一下吧。