题目:http://wenku.baidu.com/view/602da2d4240c844769eaee55.html
1.-7的二进制补码 (D)
(1)-7的原码 1000 0111
(2)符号位不变 1000 0111
(3)数值位取反 1111 1000
(4)加1 1111 1001
注意:
(1)正整数的补码与原码相同
(2)补码转化为原码
补码的符号位为‘0’,原码就补码
补码的符号位为‘1’,原码就是补码的补码
2.四种介质,带宽最大:(C)
A 同轴电缆 B 双绞线 C 光纤 D 同步线
注:
(1)双绞线也称为双扭线,是最古老但又最常用的传输媒体。把两根互相绝缘的铜导线并排放在一起,然后用规则的方法绞合起来(这样做是为了减少相邻的导线的电磁干扰)而构成双绞线.
双绞线分为1类到5类,局域网中常用的为3类,4类和5类双绞线。 3类线用于语音传输及最高传输速率为 10Mbps的数据传输;4类线用于语音传输和最高传输速率为 16Mbps的数据传输;5类线用于语音传输和最高传输速率为 100Mbps的数据传输
(2)同轴电缆由内导体铜质芯线,绝缘层,网状编制的外导体屏蔽层及保护塑料外层组成 ,内导体和外导体构成一组线对。由于外导体屏蔽层的作用,同轴电缆具有很好的抗干扰性。
同轴电缆可以将 10Mb/S的基带数字信号传送1千米到 1.2千米,因此被广泛用于局域网中
(3)光纤通信就是利用光导纤维传递光脉冲来进行通信,而光导纤维是光纤通信的媒体。光纤在任何时间都只能单向传输,因此,要实行双向通信,它必须成对出现,一个用于输入,一个用于输出,光纤两端接到光学接口上。
光纤的传输系统比同轴电缆大的多,一般小同轴电缆的最大传输带宽为 20MHz左右,中同轴电缆的最大传输带宽为 60MHz左右。单根光导纤维的数据传输速率能达几Gbps,在不使用中继器的情况下,传输距离能达几十公里。
3. 进程阻塞原因 (A)
A.时间片切换 B.等待I/O C.进程sleep D.等待解锁
如果没有时间片轮转,那么进程就没法切换了,一个进程将独享CPU。但是不能称时间片切换导致进程阻塞。
注:
(1)进程,概念主要有两点:
第一,进程是一个实体。每一个进程都有它自己的地址空间,一般情况下,包括文本区域(text region)、数据区域(data region)和堆栈(stack region)。
文本区域存储处理器执行的代码;
数据区域存储变量和进程执行期间使用的动态分配的内存;
堆栈区域存储着活动过程调用的指令和本地变量。
第二,进程是一个“执行中的程序”。程序是一个没有生命的实体,只有处理器赋予程序生命时,它才能成为一个活动的实体,我们称其为进程。
(2)进程的三种基本状态
进程在运行中不断地改变其运行状态。通常,一个运行进程必须具有以下三种基本状态。
就绪(Ready)状态 当进程已分配到除CPU以外的所有必要的资源,只要获得处理机便可立即执行,这时的进程状态称为就绪状态。
执行(Running)状态当进程已获得处理机,其程序正在处理机上执行,此时的进程状态称为执行状态。
阻塞(Blocked)状态 正在执行的进程,由于等待某个事件发生而无法执行时,便放弃处理机而处于阻塞状态。引起进程阻塞的事件可有多种,例如,等待I/O完成、申请缓冲区不能满足、等待信件(信号)等。
进程三种状态间的转换
一个进程在运行期间,不断地从一种状态转换到另一种状态,它可以多次处于就绪状态和执行状态,也可以多次处于阻塞状态。图3_4描述了进程的三种基本状态及其转换。
(1) 就绪→执行 处于就绪状态的进程,当进程调度程序为之分配了处理机后,该进程便由就绪状态转变成执行状态。
(2) 执行→就绪 处于执行状态的进程在其执行过程中,因分配给它的一个时间片已用完而不得不让出处理机,于是进程从执行状态转变成就绪状态。
(3) 执行→阻塞 正在执行的进程因等待某种事件发生而无法继续执行时,便从执行状态变成阻塞状态。
(4) 阻塞→就绪 处于阻塞状态的进程,若其等待的事件已经发生,于是进程由阻塞状态转变为就绪状态。
关于进程的一些介绍 http://oa.gdut.edu.cn/os/multimedia/oscai/chapter2/pages/ch22.htm#页头
4.设只含根节点的二叉树高度为1,现有一颗高度为h(h>1)的二叉树上只有出度为0和出度为2的节点,那么这颗二叉树节点最少为:
A.2^h-1 B.2h-1 C.2h D.2h+1
取H=1 则可以排除C和D
有个讨巧的方法:直接取h=3,画个图看下,显然是5,所以答案为B。
下面来分析下:如果每个节点出度要么为0要么为2,那么也就是要么自己为叶子,要么自己拥有左右儿子。那么什么情况下节点最少呢?直接沿着一条路下去保持出度为2,直到高度达到h,那么此时节点总数:2h-1。
5.给定下面程序,那么执行printf("%d\n",foo(20,13));结果是多少:
- int foo(int x,int y)
- {
- if(x <= 0 || y <= 0)return 1;
- return 3*foo(x-6,y/2);
- }
A.3 B.9 C.27 D.81
解:foo(20,13)->3*foo(14,6)->9*foo(8,3)->27*foo(2,1)->81foo(-4,0)=81
6.对于以下说法错误的是:
A.Dijkstra是求两点间最短路径的,复杂度:O(n^2)。
B.Floyd-Warshall是求所有点对之间最短路径的,复杂度:O(n^3)。
C.求n个数中的中位数复杂度最低为:O(n*logn)。
D.基于比较的排序算法复杂度下界为:O(n*logn)。
注:
(1)Dijkstra
http://jpkc.xaau.edu.cn/sjjg/datastru/zxxx/View/6.5.html
http://jpkc.xaau.edu.cn/sjjg/datastru/zxxx/six%20lesson/642.html
一个按路径长度递增的次序产生最短路径的算法。
该算法的基本思想是:
设置两个顶点的集合S和T=V-S,集合S中存放已找到最短路径的顶点,集合T存放当前还未找到最短路径的顶点。初始状态时,集合S中只包含源点v0,然后不断从集合T中选取到顶点v0路径长度最短的顶点u加入到集合S中,集合S每加入一个新的顶点u,都要修改顶点v0到集合T中剩余顶点的最短路径长度值,集合T中各顶点新的最短路径长度值为原来的最短路径长度值与顶点u的最短路径长度值加上u到该顶点的路径长度值中的较小值。此过程不断重复,直到集合T的顶点全部加入到S中为止。
伪代码:
1 function Dijkstra(G, w, s)
2 for each vertex v in V[G] // 初始化
3 d[v] := infinity
4 previous[v] := undefined
5 d[s] := 0
6 S := empty set
7 Q := set of all vertices
8 while Q is not an empty set // Dijstra算法主体
9 u := Extract_Min(Q)
10 S := S union {u}
11 for each edge (u,v) outgoing from u
12 if d[v] > d[u] + w(u,v) // 拓展边(u,v)
13 d[v] := d[u] + w(u,v)
14 previous[v] := u
如果我们只对在s和t之间寻找一条最短路径的话,我们可以在第9行添加条件如果满足u=t的话终止程序。
现在我们可以通过迭代来回溯出s到t的最短路径
1 S := empty sequence
2 u := t
3 while defined u
4 insert u to the beginning of S
5 u := previous[u]
现在序列S就是从s到t的最短路径的顶点集.
见:http://wiki.mbalib.com/wiki/Dijkstra%E7%AE%97%E6%B3%95
第一个for循环的时间复杂度是O(n),第二个for循环共进行n-1次,每次执行的时间是O(n)。所以总是的时间复杂度是O(n2)。如果用带权的邻接表作为有向图的存储结构,则虽然修改D的时间可以减少,但由于在D向量中选择最小的分量的时间不变,所以总的时间仍为O(n2)。
(2)Floyd-Warshall 算法
Floyd-Warshall算法,简称Floyd算法,用于求解任意两点间的最短距离,时间复杂度为O(n^3)。
Floyd-Warshall算法的原理是动态规划。
设Di,j,k为从i到j的只以(1..k)集合中的节点为中间结点的最短路径的长度。
- 若最短路径经过点k,则Di,j,k = Di,k,k − 1 + Dk,j,k − 1;
- 若最短路径不经过点k,则Di,j,k = Di,j,k − 1。
因此,Di,j,k = min(Di,k,k − 1 + Dk,j,k − 1,Di,j,k − 1)。
在实际算法中,为了节约空间,可以直接在原来空间上进行迭代,这样空间可降至二维。
Floyd-Warshall算法的描述如下:
1 void Floyd(){
2 int i,j,k;
3 for(k=1;k<=n;k++)
4 for(i=1;i<=n;i++)
5 for(j=1;j<=n;j++)
6 if(dist[i][k]+dist[k][j]7 dist[i][j]=dist[i][k]+dist[k][j];
8 }
http://www.cppblog.com/mythit/archive/2009/04/21/80579.aspx
http://www.cnblogs.com/obama/p/3348202.html
http://baike.sogou.com/v1953740.htm
(3)n个数中的中位数复杂度最低多少?
中位数就是一系列数字中,大小处于中间的那个,比方 1 2 3 4 5 的中位数是 3 ,这是奇数的情况,中位数只有一个;如果是 1 2 3 4 5 6 的话,me 们称 3 为上中位数,4 为下中位数,对于偶数来说是有 2 个,通常不特指的话,就指前一个,也就是上中位数。这里提个小细节,如果是 1 2 3 4 ... n,的中位数(中间的数)是第几个呢?O__O"…,这个很简单,但是 maybe 有些人还不大了解,中位数是第 (n+1)/2 的那个,如果是奇数的话,结果正好是个整数;如果是偶数的话,把那个 0.5 去掉吧。
在大小未必有序的 n 个数中寻找第 (n+1)/2 个数,就不是那么容易,当然如果有序就好了。自然而然的,me 们使用一个排序算法来对 n 个数排个序,然后找中位数就可以了;实际如果有序的话,寻找第 k 大的数和寻找中位数应该说是一样的,都是线性扫描一下,扫描的复杂度 O(n)。排序算法中很出名的一个就是快速排序吧,不过时间复杂度是 O(nlogn),这是平均情况下的,而最坏情况下达到 O(n^2)。如果使用排序来解决中位数问题的话,时间复杂度和排序复杂度一样,因为对于 O(nlogn) 或是 O(n^2) 来说, +O(n) 和没有 + 一样。
寻找中位数的时候使用了快速排序,而是这两个算法使用了一个同一个预处理结构 —— 划分,然后都是递归解决!中位数的也是根据一个数把原来的数划分一下,形成两部分。如果前半部分足够长,就在前部分找,否则在后半部分找!(这不仅适合中位数,实际上适合寻找第 k 大的数!!而 select_middle 其实不是来寻找中位数,是在寻找第 nth 大的数,如果 nth == (n+1)/2,这就是中位数!)
寻找中位数的程序,不,是寻找第 k 大数的程序,那样写有神马好处?它的复杂度能低于 O(nlogn) 吗?!基于划分的求 nth 大的数的那个程序,最坏情况是 O(n^2),平均是 O(n) ! O__O"…
(快速排序和寻找中位数)
http://ilovers.sinaapp.com/article/%E5%BF%AB%E9%80%9F%E6%8E%92%E5%BA%8F%E5%92%8C%E5%AF%BB%E6%89%BE%E4%B8%AD%E4%BD%8D%E6%95%B0
(4)基于比较的排序算法复杂度下界为:O(n*logn)
这些基于比较的排序算法最差情况下最好的时间复杂度就是O(nlogn).这点是可以通过决策树来帮助我们分析证明的。
决策树这个东西,学过人工智能之类的应该就很熟悉了,就是根据元素比较的不同情况往不同分支走,然后树将所有可能的情况都包括进去。
举一个三个元素的例子:=<9,4,6>
注意这个决策树的叶子就是n个元素的所有可能排列。一个实例的运行时间就是它走的路径的长度。所以最
差情况下的运行时间就是决策树的高度。要证明基于比较的算法最差情况下运行时间是Θ(nlogn),就是要证明决策树的高度最小就是nlogn
Theorem: 排序n个元素的任意决策树的高度 Ω(nlgn).
Proof: 上面提到过树最少要有n!个叶子。而高度为h的二叉树的叶子数最多是(满的时候)2h个叶子,即
n!≤2h
h≥lg(n!)
≥ lg ((n/e)n) (Stirling’s formula)
= nlg n–nlg e
= Ω(nlg n)
于是就得到结论,基于比较的排序算法下界是Ω(nlg n)
http://www.cnblogs.com/soyscut/p/3380781.html
http://lumiafan.diandian.com/post/2010-12-11/16426568
7.给定一个m行n列的整数矩阵,每行从左到右和每列从上到下都是有序(假设都是升序)的。判断一个整数k是否在矩阵中出现的最优算法,在最坏情况下的时间复杂度是
A.O(m*n) B.O(m+n) C.O(log(m*n)) D.O(log(m+n))
1 5 | 7 9
4 6 | 10 15
8 11| 12 19
14 16| 18 21
从右上角开始,遍历每列(小于该列第一个值,即可去除该行)和每行,剑指OFFER上的题目
8.一个包里有5个黑球,10个红球和17个白球。每次可以从中取两个球出来,放置在外面。那么至少取多少次,一定出现过取出一对颜色一样的球。
A.16 B.9 C.4 D.1
极限情况是:前十次每次取1个红球和1个白球,中间五次,每次取1个黑球和1个白球。最后当第十六次的时候才能取到一对颜色相同的球。所以至少要十六次。
9.选C
最长8位 最短3位, 3位都是1开头
最短3位有10^2=100种,
四位:10^4=10000,五位:10^5=100000,六位:10^6=1000000,七位:10^7=10000000,八位:10^8=10000000
一位号码4BITE,
其实是比较前7位,相加 11110101*4*8/4/1024(Kb)/1024(Mb)=42MB 取(50Mb)
讨论解:存储八位需要4byte *10000000(用户级别)/1024/2014=39MB
10.骑士只说真话,骗子只说假话。下列场景能确定一个骑士、一个骗子的有?
A.甲说:“我们中至少有一个人说真话”,乙什么也没说。
B.甲说:"我们两个都是骗子",乙什么也没说。
C.甲说:“我是个骗子或者乙是个骑士”,乙什么也没说。
D.甲乙都说:“我是个骑士”。
E.甲说:“乙是个骑士”,乙说:“我们俩一个是骑士一个是骗子”。
分析一下:是道逻辑题。
A.如果甲是骑士,那么因为至少一个人说真话,那么有可能乙也说真话。那么可能甲乙都是骑士。如果甲是骗子,那么没有一个人说真话,那么都是骗子。排除。
B.如果甲是骑士,那么不可能说这样的话,因为骑士不会说自己是骗子。那么甲是骗子,甲说的是假话,那么至少一个不是骗子。那么乙就是骑士。可以。
C.如果甲是骑士,那么必然乙也是骑士。不符合。如果甲是骗子,那么必然乙也不是骑士,这句话才能是假的。排除。
D.如果甲乙都是骑士,显然成立。排除。
E.如果甲是骑士,那么乙也是骑士,与乙说的话矛盾。如果甲是骗子,那么乙必然不是骑士。
11 某服务强求经复杂均衡设备分配到集群A、B、C、D进行处理响应的概率分别是10%、20%、30%、40%,已知测试集所得稳定指标分别是90%,95%,99%,99.9%。现在该服务请求处理失败,且已排除稳定性意外的问题,那么最有可能在处理该服务请求的集群是:
A. B. C. D.
解:A B 10%*10%,20%*5%,30%*1%,40%*0.1%
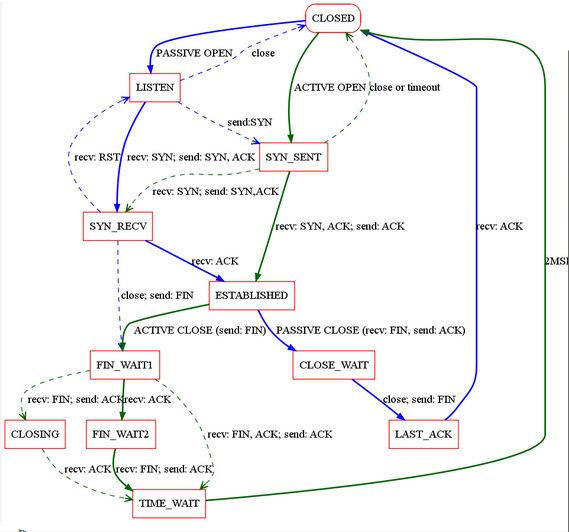
12.以下是TCP连接关闭过程中出现的状态
A.listen B time_wait C last_ack D syn-received
参考这个链接 选BC
http://liujianguangaaa.iteye.com/blog/975445
13.C
甲 出6 乙<6 则甲赔,乙>6 则乙赔
14.没有一对元素被比较过两次或者以上,则是节俭算法,下面是节俭排序的算法是:
A.插入排序 B.选择排序 C 堆排序 D归并排序
插入排序:插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中,从而得到一个新的、个数加一的有序数据,算法适用于少量数据的排序,时间复杂度为O(n^2)。每次处理就是将无序数列的第一个元素与有序数列的元素从后往前逐个进行比较,找出插入位置,将该元素插入到有序数列的合适位置中。
选择排序:选择排序是给每个位置选择当前元素最小的,比如给第一个位置选择最小的,在剩余元素里面给第二个元素选择第二小的,依次类推,直到第n-1个元素,第n个元素不用选择了,因为只剩下它一个最大的元素了。
堆排序 堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,可以利用数组的特点快速定位指定索引的元素。堆排序利用了大根堆(或小根堆)堆顶记录的关键字最大(或最小)这一特征,使得在当前无序区中选取最大(或最小)关键字的记录变得简单。
(1)用大根堆排序的基本思想
① 先将初始文件R[1..n]建成一个大根堆,此堆为初始的无序区
② 再将关键字最大的记录R[1](即堆顶)和无序区的最后一个记录R[n]交换,由此得到新的无序区R[1..n-1]和有序区R[n],且满足R[1..n-1].keys≤R[n].key
③由于交换后新的根R[1]可能违反堆性质,故应将当前无序区R[1..n-1]调整为堆。然后再次将R[1..n-1]中关键字最大的记录R[1]和该区间的最后一个记录R[n-1]交换,由此得到新的无序区R[1..n-2]和有序区R[n-1..n],且仍满足关系R[1..n-2].keys≤R[n-1..n].keys,同样要将R[1..n-2]调整为堆。
……
直到无序区只有一个元素为止。
(2)大根堆排序算法的基本操作:
① 初始化操作:将R[1..n]构造为初始堆;
② 每一趟排序的基本操作:将当前无序区的堆顶记录R[1]和该区间的最后一个记录交换,然后将新的无序区调整为堆(亦称重建堆)。
归并操作(merge),也叫归并算法,指的是将两个顺序序列合并成一个顺序序列的方法。将序列每相邻两个数字进行归并操作(merge),形成floor(n/2)个序列,排序后每个序列包含两个元素将上述序列再次归并,形成floor(n/4)个序列,每个序列包含四个元素重复步骤2,直到所有元素排序完毕
如 设有数列{6,202,100,301,38,8,1}
初始状态:6,202,100,301,38,8,1
第一次归并后:{6,202},{100,301},{8,38},{1},比较次数:3;
第二次归并后:{6,100,202,301},{1,8,38},比较次数:4;
第三次归并后:{1,6,8,38,100,202,301},比较次数:4;
总的比较次数为:3+4+4=11;
15.补全下面的快排程序
void qsort(int* array , int Ien){
int value,start,end;
if(len <= 1) return;
value = array[0];
start = 0;
end = len - 1;
while (start < end) {
for (; start < end; --end){
if (array[ end ] < value){
array[ start ++] = array[ end ];
break;
}
}
for (; end > start; ++start){
if (array[ start ] > value){
array [end -- ] = array[ start ];
break;
}
}
array[ start ] =value;
qsort(array, start);
qsort( array+start+1 , len-start-1);
16. 网络最大流量
17 公司只要一个员工过生日,所有员工 全部放假一天。其余时候员工都没有假期,必须上班。假设一年365天,每个员工的生日都概率均等地分布在365天,那么,公司雇佣多少员工,可以使公司一年内所有员工的总工作时间期望最大。
一下是偶的详解:
18
思路
(1) 非正整数
从头开始判断 a[0]与0的大小,若a[0]<0 下标加一,
若 a[i]=i ,则输出a[i], 下标加一;
若 a[i]>i ,中间不需要判断 直接判断a[a[i]+1]的值,
循环至最后一个元素。
(2) 正整数 二分查找
19 智商题
鳄鱼为偶数时,两条鳄鱼相互制约,只要其中一条鳄鱼先发起进攻他就会被吃掉,所以聪明的鳄鱼都会处于僵持状态,怪物安全。
鳄鱼为奇数,最先吃怪物的鳄鱼在进食过程中,剩余偶数条鳄鱼,相互制约,所以第一吃怪物的鳄鱼被吃的风险很小,聪明的鳄鱼都想第一个吃怪物,所以怪物不安全。
20
浏览器首先查询DNS服务器,将www.taobao.com转换成ip地址。在不同的地区或者不同的网络(电信、联通、移动)的情况下,转换后的ip地址很可能是不一样的,这首先涉及到负载均衡的第一步,通过DNS解析域名时将你的访问分配到不同的入口,同时尽可能保证你所访问的入口是所有入口中可能较快的一个(这和后文的CDN不一样)。
通过这个入口成功的访问了www.taobao.com的实际的入口ip地址。这时产生了一个PV,即Page View,页面访问。每日每个网站的总PV量是形容一个网站规模的重要指标。淘宝网全网在平日(非促销期间)的PV大概是16-25亿之间。同时作为一个独立的用户,这次访问淘宝网的所有页面,均算作一个UV(Unique Visitor用户访问)。最近臭名昭著的12306.cn的日PV量最高峰在10亿左右,而UV量却远小于淘宝网十余倍。
因为同一时刻访问www.taobao.com的人数过于巨大,所以即便是生成淘宝首页页面的服务器,也不可能仅有一台。仅用于生成www.taobao.com首页的服务器就可能有成百上千台,那么一次访问时生成页面的任务便会被分配给其中一台服务器完成。这个过程要保证公正、公平、平均(暨这成百上千台服务器每台负担的用户数要差不多),这一很复杂的过程是由几个系统配合完成,其中最关键的便是LVS,Linux Virtual Server,世界上最流行的负载均衡系统之一,正是由目前在淘宝网供职的章文嵩博士开发的。
经过一系列复杂的逻辑运算和数据处理,用于这次给你看的淘宝网首页的HTML内容便生成成功了。对web前端稍微有点常识的童鞋都应该知道,下一步浏览器会去加载页面中用到的css、js、图片等样式、脚本和资源文件。但是可能相对较少的同学才会知道,你的浏览器在同一个域名下并发加载的资源数量是有限制的,例如ie6-7是两个,ie8是6个,chrome各版本不大一样,一般是4-6个。访问淘宝网首页需要加载126个资源,那么如此小的并发连接数自然会加载很久。所以前端开发人员往往会将上述这些资源文件分布在好多个域名下,变相的绕过浏览器的这个限制,同时也为下文的CDN工作做准备。
据不可靠消息,在双十一当天高峰,淘宝的访问流量最巅峰达到871GB/S。这个数字意味着需要178万个4mb带宽的家庭宽带才能负担的起,也完全有能力拖垮一个中小城市的全部互联网带宽。那么显然,这些访问流量不可能集中在一起。并且大家都知道,不同地区不同网络(电信、联通等)之间互访会非常缓慢,但是很少发现淘宝网访问缓慢。这便是CDN,Content Delivery Network,即内容分发网络的作用。淘宝在全国各地建立了数十上百个CDN节点,利用一些手段保证访问的(这里主要指js、css、图片等)地方是最近的CDN节点,这样便保证了大流量分散已经在各地访问的加速。
这便出现了一个问题,那就是假若一个卖家发布了一个新的宝贝,上传了几张新的宝贝图片,那么淘宝网如何保证全国各地的CDN节点中都会同步的存在这几张图片供用户使用呢?这里边就涉及到了大量的内容分发与同步的相关技术。淘宝开发了分布式文件系统TFS(taobao file system)来处理这类问题。
(终于加载完了淘宝首页,习惯性的在首页搜索框中输入了'毛衣'二字并敲回车,这时你又产生了一个PV,然后,淘宝网的主搜索系统便开始为你服务了。它首先对你输入的内容基于一个分词库进行的分词操作。众所周知,英文是以词为单位的,词和词之间是靠空格隔开,而中文是以字为单位,句子中所有的字连起来才能描述一个意思。例如,英文句子I am a student,用中文则为:“我是一个学生”。计算机可以很简单通过空格知道student是一个单词,但是不能很容易明白“学”、“生”两个字合起来才表示一个词。把中文的汉字序列切分成有意义的词,就是中文分词,有些人也称为切词。我是一个学生,分词的结果是:我 是 一个 学生。
进行分词之后,还需要根据你输入的搜索词进行你的购物意图分析。用户进行搜索时常常有如下几类意图:(1)浏览型:没有明确的购物对象和意图,边看边买,用户比较随意和感性。Query例如:”2010年10大香水排行”,”2010年流行毛衣”, “zippo有多少种类?”;(2)查询型:有一定的购物意图,体现在对属性的要求上。Query例如:”适合老人用的手机”,”500元 手表”;(3)对比型:已经缩小了购物意图,具体到了某几个产品。Query例如:”诺基亚E71 E63″,”akg k450 px200″;(4)确定型:已经做了基本决定,重点考察某个对象。Query例如:”诺基亚N97″,”IBM T60″。通过对你的购物意图的分析,主搜索会呈现出完全不同的结果来。
之后的数个步骤后,主搜索系统便根据上述以及更多复杂的条件列出了搜索结果,这一切是由一千多台搜索服务器完成。然后你开始逐一点击浏览搜索出的宝贝。你开始查看宝贝详情页面。经常网购的亲们会发现,当你买过了一个宝贝之后,即便是商家多次修改了宝贝详情页,你仍然能够通过‘已买到的宝贝’查看当时的快照。这是为了防止商家对在商品详情中承诺过的东西赖账不认。那么显然,对于每年数十上百亿比交易的商品详情快照进行保存和快速调用不是一个简单的事情。这其中又涉及到数套系统的共同协作,其中较为重要的是Tair,淘宝自行研发的分布式KV存储方案。
然后无论你是否真正进行了交易,你的这些访问行为便忠实的被系统记录下来,用于后续的业务逻辑和数据分析。这些记录中访问日志记录便是最重要的记录之一,但是前边我们得知,这些访问是分布在各个地区很多不同的服务器上的,并且由于用户众多,这些日志记录都非常庞大,达到TB级别非常正常。那么为了快速及时传输同步这些日志数据,淘宝研发了TimeTunnel,用于进行实时的数据传输,交给后端系统进行计算报表等操作。
你的浏览数据、交易数据以及其它很多很多的数据记录均会被保留下来。使得淘宝存储的历史数据轻而易举的便达到了十数甚至更多个PB(1PB=1024TB=1048576GB)。如此巨大的数据量经过淘宝系统1:120的极限压缩存储在淘宝的数据仓库中。并且通过一个叫做云梯的,由2000多台服务器组成的超大规模数据系统不断的进行分析和挖掘。)
一个部分答案的讲解:http://blog.csdn.net/wonderwander6642/article/details/8062633