LeetCode——Best Time to Buy and Sell Stock III (股票买卖时机问题3)

问题：

Say you have an array for which the i^th element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete at most two transactions.

依旧还是那个熟悉的味道，如果II是I的另一个版本，那么III就是他们的一个升级版。

在这个版本中只能交易两次，也就是买卖各两次，其它条件依旧没有变（不熟悉的请参见I）

分析：

 

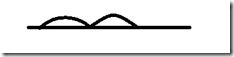
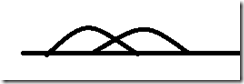
在此题中，最多只能买卖两次，而且两次交易不能有交叉，也就是说应该是这样儿的（直线为时间，弧线为交易），

  或者 

不会出现：

问题三是问交易两次的最大收益，从上面的图我们可以看出由于两次交易没有交叉，我们可以考虑把这个问题拆分为两个问题：

1.第一次交易的最大收益（在前）

2.第二次交易的最大收益（在后）

那么现在问题又来了，在哪个位置拆分呢？几经思考发现从哪儿拆分都不合适，无论从哪儿拆分都不敢保证这种拆分办法就能得出最大收益，既然哪个位置拆分都不能保证最大收益，那如果我们每个位置都拆分一次，然后比较各自的最大收益，这样是否可行呢？在股票买卖时机问题1中我们用时间复杂度O(n)解决了一次交易的最大收益问题，那么在这里，每一次拆分会产生两个组，每个组用问题1的解法解答，那每一次拆分找出最大收益的时间复杂度为O(n)，那拆分n-1次的时间复杂度就是O(n^2)了。按这种方法可以解决了，但是在LeetCode上提交貌似会报超时，而且，问题I和II都是在时间复杂度O(1)内解决的，没道理问题III要O(n^2)，我们再仔细的考虑一下……

 

在问题I中我们采用动态规划的思想，通过分阶段找最优策略，后一阶段的最优策略由前一阶段的最优策略转化而来，换个角度，我们可以认为我们从第一阶段起，我们找到了每个阶段的最优解，在这道题中，也就是我们找到了从第1天到第i天的最大收益（i=2,3,4,…,n），只是在问题I中我们并没有把这些各个阶段的最大收益值保存下来。

 

那么我们回到问题III，我们先用I的办法把数组遍历一遍，并且声明一个数组profit[n]，profit[i]保存第一天到第i+1天的最大收益，i=0,1,2,…,n-1，到此时间复杂度为O(n)。

此时相当于我们知道拆分后（假设从数组下标k处拆分）的第一组的最大收益，那么第二组呢？profit[i]只是记录了从0到i的最大收益，我们如何知道从k到i的最大收益呢？

 

再次分析问题I的解法，问题I的重点代码如下（完整的请参考http://www.cnblogs.com/chrischennx/p/4014422.html）：

for(int i=1; i<prices.length;i++){

           min = prices[i]<min?prices[i]:min;

           profit = prices[i]-min>profit?prices[i]-min:profit;

        }

它是通过找到各个阶段的最小值，然后用当前值减去最小值和前一阶段的最大收益比较得到最大收益，那么在问题III拆分后的第二组中我们是否也可以考虑用类似的办法来处理呢，每次拆分再计算k到i的最大收益肯定是不行的，因为每次时间复杂度为O(n)，拆了n-1次时间复杂度就成了O(n^2)，又回到刚开始的了，这不是我们需要的。

在问题I中是按数组从前往后考虑的，那么在第二组中，由于每次拆分都有最后一个值a[n-1]，那么索性我们第二组从最后开始考虑。问题I是考虑前边儿找一个低的价格买入，后面找个高价卖出，也就是先找买入的价格，再找卖出的价格；那么从后开始考虑可以理解为：后面找个高价卖出，前面找个低价买入，也就是先找卖出的价格，再找买入的价格。也就是这样：

for(int i=a.length-2;i>=0;i--){

            max = a[i]<max?max:a[i];

            profit2[i] = max-a[i]>profit2[i+1]?max-a[i]:profit2[i+1];

        }

然后我们就可以通过profit[i]+profit2[i]的最大值得到两次交易的最大收益。

 

到此问题就可以解决了，但是此时的空间复杂度为O(2n)，其实还有更省的：不求profit2数组。

我们如此这般：

int max = a[a.length-1];

        int result = profit[a.length-1];

        for(int i=a.length-2;i>=0;i--){

            max = a[i]>max?a[i]:max;

            result = profit[i]+max-a[i]>result?profit[i]+max-a[i]:result;

        }

其中profit[i]是按问题I的方法把求出的0到i的最大收益。

result = profit[i]+max-a[i]>result?profit[i]+max-a[i]:result;

这里用result直接用来保存最大收益，乍一看，容易理解为profit[i]+(max-a[i])和result比较，但是max-a[i]并不一定是第二组的最大收益，比如：[5,6,1,4]，当i=1的时候，a[i]=6，max=6，但是此时的profit[1]+(max-a[1])，也就是profit[1]+0，肯定没有i=2，a[i]=1,max=4的时候大，profit[2]+3，看似这么理解是对的，但是，其实是错的，因为profit[i]+max-a[i]并不是在和它自己比，而是和result比，若之前的比较中有比较大的，那么就保存到result中了，之后的值比result小，result的值就不变了，所以最终result还是最大值。

如：[5,6,1,4]这个例子，

用问题I的方法计算出profit=[0,1,1,3]，

当i=2的时候result=4，

当i=1的时候result = 1+4-4>4?1+4-4:4 = 4。

 

 

---

 

完整代码如下（java）:

public class Solution {

    public int maxProfit(int[] a) {

        if(a==null || a.length==0)return 0;

        int profit[] = new int[a.length];

        int min = a[0];

        profit[0] = 0;

        for(int i=1;i<a.length;i++){

            min = a[i]<min?a[i]:min;

            profit[i] = a[i]-min>profit[i-1]?a[i]-min:profit[i-1];

        }

        

        int max = a[a.length-1];

        int result = profit[a.length-1];

        for(int i=a.length-2;i>=0;i--){

            max = a[i]>max?a[i]:max;

            result = profit[i]+max-a[i]>result?profit[i]+max-a[i]:result;

        }

        

        return result;

    }

}