DFS和BFS概念及实践+acwing 842 排列数字(dfs) +acwing 844. 走迷宫(bfs)

DFS (深搜)， 也有说就是递归的
执着： 一直搜到底，然后回溯下一个节点
数据结构 ： stack (这里的栈，实际上是编译器内部的栈， 所以说也可以看成递归， 递归内部也是调用编译器内部栈)
空间：O(h) h： 是高度
不具有最短路性质（思路比较奇怪的，对空间要求比较高的）
重要概念： 回溯，剪枝

BFS (宽搜)
稳重：一层一层搜索
数据结构 ： queue， 空间：O(2^h) h： 是高度
具有最短路性质（当每条路权重是1）

---

DFS 例题讲解：可以用来理解递归的思想

acwing 842 排列数字

给定一个整数 n，将数字 1∼n 排成一排，将会有很多种排列方法。
现在，请你按照字典序将所有的排列方法输出。

输入格式
共一行，包含一个整数 n。
输出格式
按字典序输出所有排列方案，每个方案占一行。

数据范围
1≤n≤7
输入样例：
3
输出样例：
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

思想：
对于全排列问题，可以画出下面的搜索树

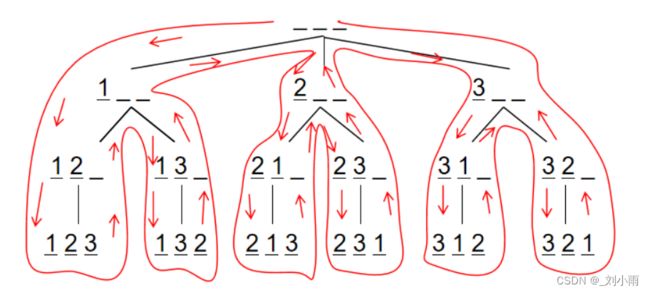
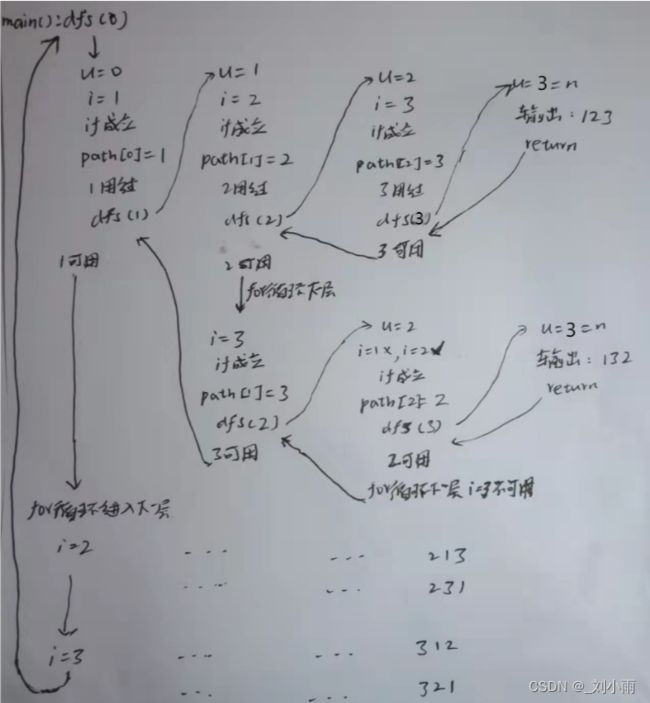
递归函数调用全过程

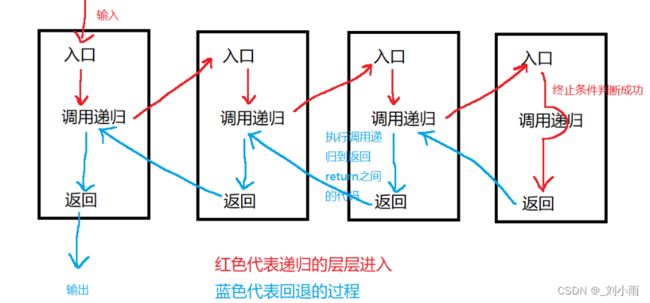
code:

// 回溯的时候是系统中自动分配的栈回调。


#include 
using namespace std;
const int N = 10;
int n;
int path[N];
bool st[N];  // 保存之前的点是否遍历  == true 表示已经过了 

void dfs(int u)
{
    if(u == n) 
    {
        // 说明所有的位置填满， 这里从0开始，在main函数中，对应的从0开始
        for(int i=0; i<n; i++) cout << path[i] << ' ';
        cout << endl;
        return;
    }
    
    // 这里是确定哪几个点可以被选择
    for(int i=1; i<=n; i++)    // 这里需要找哪些点没有被枚举
    {
        if(!st[i])
        {
            path[u] = i;
            st[i] = true;
            dfs(u+ 1);
         	// 恢复现场
            st[i] = false;
            //path[u] = 0;     // 可以删掉， 因为这里的值被覆盖掉   
        }
    }
}

int main()
{
    cin >> n;
    dfs(0);      // 从第0个位置开始看    
    return 0;
}

讲解上述代码流程：

---

BFS: 为什么能搜到最短路呢

它是一层一层搜索的，只有当图中权重是一样的，这样搜才是最短路的

DFS 一般没有常用的框架， 但是BFS 宽搜 有常用的框架， 所以看下面

常用的解法步骤：

1. 初始状态放入队列
2. 放入while， 不空
3. 在while 中 每次拿到队头
4. 扩展 队头
5. 结束

伪代码：

queue  <- 初始状态
while queue 不空
{
	t  <-  队头
	扩展  t
}

样例： acwing 844. 走迷宫

给定一个 n×m 的二维整数数组，用来表示一个迷宫，数组中只包含 0 或 1，其中 0 表示可以走的路，1 表示不可通过的墙壁。

最初，有一个人位于左上角 (1,1) 处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。

请问，该人从左上角移动至右下角 (n,m) 处，至少需要移动多少次。

数据保证 (1,1) 处和 (n,m) 处的数字为 0，且一定至少存在一条通路。

输入格式
第一行包含两个整数 n 和 m。

接下来 n 行，每行包含 m 个整数（0 或 1），表示完整的二维数组迷宫。

输出格式
输出一个整数，表示从左上角移动至右下角的最少移动次数。

数据范围
1≤n,m≤100
输入样例：
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出样例：
8

思路：

1. 用g[][] 存储地图， 用d[][] 存储起点到n，m 的距离
2. 从起点开始广度优先遍历地图
3. 当地图遍历完，就求出了起点到各点的距离，输出d[n][m]即可

#include 
#include 
#include 

using namespace std;

typedef pair<int, int> PII;

const int N = 110;
int g[N][N];  // 存储地图
int d[N][N];  // 存储距离
int n, m;

int bfs()
{
    queue<PII> q;
    q.push({0, 0});
    memset(d, -1, sizeof d);
    d[0][0] = 0;
    while(!q.empty())
    {
        PII start = q.front();
        q.pop();
        g[start.first][start.second] = 1; // 表示已经走过
        int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0 ,-1};
        for(int i =0; i < 4; i++)
        {
            int x = start.first + dx[i], y = start.second + dy[i];
            if(!g[x][y] && x >= 0 && x < n && y >= 0 && y < m && d[x][y] == -1) // 表示没有走过，说明可以选择
            {
                g[x][y] = 1;
                d[x][y] = d[start.first][start.second] + 1;
                //cout << d[x][y] << endl;
                q.push({x, y});
            }
        }
    }

    // d 数组中已经保存着能走的路径最短距离（到{0,0}）
    return d[n - 1][m - 1];
}


int main()
{
    cin >> n >> m;
    memset(g, 1, sizeof g);  // 需要初始化都不能走
    for(int i = 0; i < n; i ++)
        for(int j =0; j < m; j ++)
            cin >> g[i][j];
    cout << bfs() << endl;
    
    return 0;
}

下面是如果想输出走的路径代码

思路： 从最后的位置倒着输出
方法： 用Pre[][] 保存上一个点的位置信息

#include 
#include 
#include 

using namespace std;

typedef pair<int, int> PII;

const int N = 110;
int g[N][N];  // 存储地图
int d[N][N];  // 存储距离
int n, m;

PII Pre[N][N];  // 保存走过的点

int bfs()
{
    queue<PII> q;
    q.push({0, 0});
    memset(d, -1, sizeof d);
    d[0][0] = 0;
    while(!q.empty())
    {
        PII start = q.front();
        q.pop();
        g[start.first][start.second] = 1; // 表示已经走过
        int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0 ,-1};
        for(int i =0; i < 4; i++)
        {
            int x = start.first + dx[i], y = start.second + dy[i];
            if(!g[x][y] && x >= 0 && x < n && y >= 0 && y < m && d[x][y] == -1) // 表示没有走过，说明可以选择
            {
                g[x][y] = 1;
                Pre[x][y] = start;
                d[x][y] = d[start.first][start.second] + 1;
                //cout << d[x][y] << endl;
                q.push({x, y});
            }
        }
    }
    
    // 下面是从最后将路径输出出来
    int x = n - 1, y = m - 1;
    while(x || y)
    {
        cout << x << ' ' << y << endl;
        auto t = Pre[x][y];
        x = t.first, y= t.second;
    }

    // d 数组中已经保存着能走的路径最短距离（到{0,0}）
    return d[n - 1][m - 1];
}


int main()
{
    cin >> n >> m;
    memset(g, 1, sizeof g);  // 需要初始化都不能走
    for(int i = 0; i < n; i ++)
        for(int j =0; j < m; j ++)
            cin >> g[i][j];
    cout << bfs() << endl;
    
    return 0;
}

运行结果如下：