FIR数字滤波器设计——频率抽样法

实验目的

本实验结合教材中FIR数字滤波器设计的教学内容,学习和掌握频率抽样法设计FIR数字滤波器的原理和实现过程,学习MATLAB设计FIR 数字滤波器的相关函数的使用,掌握使用MATLAB设计FIR数字滤波器的过程与方法,通过调整过渡点以及滤波器长度等参数,观察其对滤波特性的影响,从而加深对FIR 数字滤波器常用指标和设计过程的理解。

所使用的主要函数

B=fir2(N,R,A):设计一个N阶的FIR数字滤波器，其频率响应由向量F和A指定，滤波器的系数(单位冲激响应)返回向量B中，长度为N+1。向量F和A分别指定滤波器的抽样点的频率及其幅值，所期望的滤波器的频率响应可用plot(F,A)绘出(F为横坐标，A为纵坐标)。F中的频率必须在0.0到1.0之间，1.0对应于抽样频率的一半。它们必须按递增的顺序从0.0开始到1.0结束。

B=fir2(N,R,A,win),:用指定的窗函数设计FIR数字滤波器，其窗函数包括Boxcar、Hann、Bartlett、Blackman、Kaiser以及Chebwin等，例如，B=fir2(N,R,bartlett(N+1),使用的是三角窗；B=fir2(N,R,M,chebwin(N+1,R),使用的是切比雪夫窗。缺省情况下，函数fir2使用的Hamming窗。

实验内容

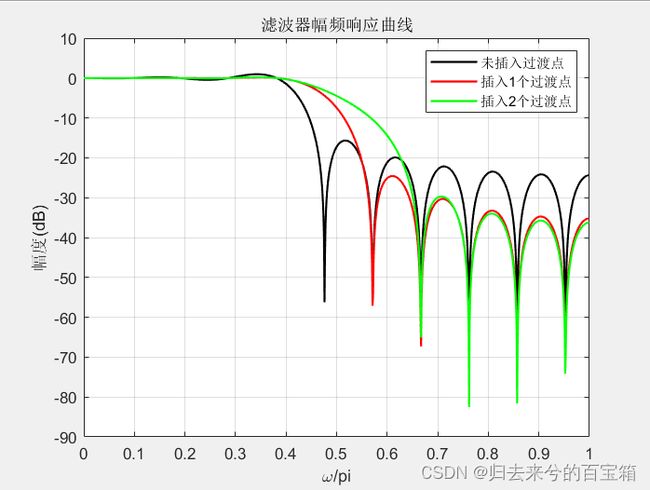
用频率抽样法设计一个FIR数字低通滤波器。滤波器满足指标：通带边界频率fp=800Hz, 阻带边界频率fs=1000Hz, 通带波纹0.5dB, 阻带最小衰减为40dB, 抽样频率4000Hz。若分别设置0，1，2个过渡点，比较设计所得的滤波器幅频响应曲线。

实验代码 

 clc;clear all;close all;
fc=4000;
ap=0.5;as=40;fp=800;fs=1000;
wp=2*pi*fp/fc;
ws=2*pi*fs/fc;
 
N_t=2*pi/(ws-wp);%20
N=21;
wc=(ws+wp)/2;
N_c=wc/2/pi*21;%4.725
 
 
a=(N-1)/2;
k=0:floor((N-1)/2);k2=floor((N-1)/2)+1:N-1;
angH=[-a*(2*pi)/N*k,a*(2*pi)/N*(N-k2)];
 
%未插入过渡点
Hrs=[ones(1,5),zeros(1,12),ones(1,4)];
Hb=Hrs.*exp(j*angH);
h=real(ifft(Hb,N));
[Hb,w]=freqz(h,1,1000);
mag=abs(Hb);Hdb=20*log10(mag);
 
%插入一个过渡点
Hrs1=[ones(1,5),0.6,zeros(1,10),0.6,ones(1,4)];
Hb1=Hrs1.*exp(j*angH);
hbl=real(ifft(Hb1,N));
[Hb1,w1]=freqz(hbl,1,1000);
mag1=abs(Hb1);Hdb1=20 * log10(mag1) ;
 
%插入两个过渡点
Hrs2=[ones(1,5),0.7,0.3,zeros(1,8),0.3,0.7,ones(1,4)];
Hb2=Hrs2.*exp(j*angH);
hb2=real(ifft(Hb2,N));
[Hb2,w2]=freqz(hb2,1,1000);
mag2=abs(Hb2);Hdb2=20*log10(mag2) ;
 
 
figure(1);
plot(w/pi,Hdb,'k','LineWidth',1.3); 
grid on; hold on;
plot(w1/pi,Hdb1,'r','LineWidth',1.3) ; 
hold on;
plot(w2/pi,Hdb2,'g','LineWidth',1.3) ; 
hold off;
xlabel('\omega/pi') ; ylabel('幅度(dB)') ;title('滤波器幅频响应曲线')
legend('未插入过渡点','插入1个过渡点','插入2个过渡点')

实验结果

 

上图显示：滤波器长度相同，插入过滤点数越多，过渡带越宽，阻带衰减越大，

与理论相符合。

如何降低通带和阻带的波动？

1.增加过渡点数，会增大阻带的衰减，增加过渡带宽度；原因是过度点可以减弱抽样点突变引起的起伏振荡。

2.增加长度N，可以增大阻带衰减而不增大过渡带宽。由此减少波动。

3.增强系统性能。