5.java数据结构与算法 ---- 第七章 八大排序(冒泡；选择；插入/希尔；快排；归并；基数)

排序

冒泡排序

有手就行
上代码:

public static void bubbleSort(int[] arr) {
    int temp = 0;//零时变量,用于交换
    boolean flag = false;//用于判断是否进行过交换
    for (int i = 0; i < arr.length - 1; i++) {
        for (int j = 0; j < arr.length - 1; j++) {
            //从小到大
            if (arr[j] > arr[j + 1]) {
                temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
                flag = true;
            }
        }
        if (flag) {
            //true 进行过交换
            flag = false;//重置
        } else {
            //此次循环没有进行过交换,说明已经有序了
            break;
        }
    }
}

选择排序

有手就行
每次排序选最小的调到前面来
上代码:

public static void selectSort(int[] arr) {
    int temp;

    for (int i = 0; i < arr.length - 1; i++) {
        int k = i; //记录最大值的下标
        int max = arr[i];//记录最大值
        for (int j = i + 1; j < arr.length; j++) {
            if (arr[j] > max) {//重置最大值和下标
                max = arr[j];
                k = j;
            }
        }

        if (k != i) {//最大值的下标发生了改变,才交换---算是一种优化方式
            temp = arr[k];
            arr[k] = arr[i];
            arr[i] = temp;
        }
    }
}

插入排序

这个不太好理解了
中途图解展示:
上代码:

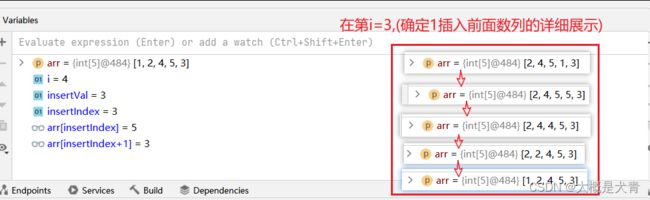
public static void insertSort(int[] arr) {
    int insertVal;
    int insertIndex;
    //{5, 2, 4, 1, 3};
    for (int i = 1; i < arr.length; i++) {//从1开始!
        insertVal = arr[i];//保存当前待插入的数据,简称摇摆数
        insertIndex = i - 1;//保存前一个索引,
        while (insertIndex >= 0 && insertVal < arr[insertIndex]){
            //待插入的数,比前面的索引数字小; 把前部分数组整体后移
            //
            arr[insertIndex+1] = arr[insertIndex];
            insertIndex--;
        }
        if(insertIndex!=i-1);{//提升效率的细节
            arr[insertIndex+1] = insertVal;
        }
    }
}

这个代码很精致了!

直接插入排序存在的

希尔排序

1.引入
插入排序存在的问题,arr[] = {2,3,4,5,6,1}
这里的1(最小),需要后移的次数很多.
当需要插入的数是较小的数,后移的次数明显增多,影响效率

由此进一步引出希尔排序!!

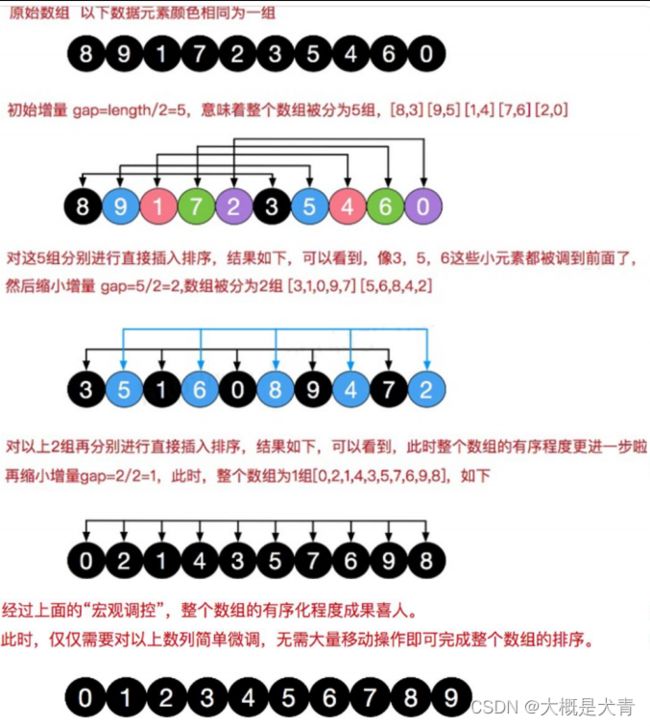
2.希尔排序介绍:
一种经过优化的插入排序,(缩小增量排序)

思路:
按照下标做一定的分组,对每组直接插入排序;随着增量逐渐减少,越来越接近有序.

示意图:

上代码:
先交换法----优化到移位法

    /**
     * 希尔排序-交换法
     * @param arr
     */
public static void shellSort1(int[] arr) {

    int temp =0;

    for (int gap = arr.length / 2; gap > 0; gap /= 2) {
        for (int i = gap; i < arr.length; i++) {
            for (int j = i - gap; j >=0 ; j-= gap) {
                //如果当前元素大于加上步长后的那个元素,交换,个人感觉很像冒泡
                if(arr[j]> arr[j+gap]){
                    temp = arr[j];
                    arr[j] = arr[j+gap];
                    arr[j+gap] = temp;
                }
            }
        }
    }
}


/**
 * 希尔排序-移位法
 * @param arr
 */
public static void shellSort2(int[] arr) {
    for (int gap = arr.length / 2; gap > 0; gap /= 2) {

        for (int i = gap; i < arr.length; i++) {//这里if优化可以加到最后的给temp赋值那里..
            int j = i;//记录待插入的元素值
            int temp = arr[j];//临时变量记录要插入的数

            //找位置
            if (arr[j] < arr[j - gap]) {
                while (j - gap >= 0 && temp < arr[j - gap]) {
                    arr[j] = arr[j - gap];
                    j -= gap;
                }
                //当退出while后,就给temp找到插入位置
                arr[j] = temp;
            }
        }
    }
}

快速排序

简介:快排是对冒泡的一种改进

基本思想:分割成两个部分,其中的一部分比另一部分的数据都要小;然后再按照这个方法对两个部分的数据快速排序,整个过程可以递归进行

流程示意图:
快排–区别于韩顺平,pivot的选择是每次的最左边的数字—其中需要注意的是,顺序很重要…

上代码:

/**
     * 思路:
     * 1.确定基准数
     * 2.先从右边开始,找小数;后从左边开始找大数;在ij不重叠之前满足条件的交换位置
     * 3.当ij重合后,基准数归位 --- i,j重合位置和基准数交换
     * 4.递归
     * @param arr
     * @param left
     * @param right
     */
    private static void quickSort3(int[] arr, int left, int right) {
        if (left >= right) return;
        int pivot = arr[left]; //永远以最左边的数为基准
        int i = left, j = right;
        while (i < j) {//顺序很重要
            while (arr[j] >= pivot && i < j) --j; //从右向左遇到小于基准的数就停止
            while (arr[i] <= pivot && i < j) ++i; //从左向右遇到大于基准的数就停止
            if (i < j) { //交换
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }
        //基准数归位（位置已确定） --- 此时i,j必然是重合的,交换i和基准数的位置
        arr[left] = arr[i];
        arr[i] = pivot;

        //分别对基准数两端的子数组进行快排
        quickSort3(arr, left, i - 1);
        quickSort3(arr, i + 1, right);
    }

    @Test
    public void test_quickSort3() {
        int[] arr = {2, 4, 1, 3, 0, 7, 9, 3};
        quickSort3(arr, 0, 7);

        for (int val : arr) {
            System.out.print(val + " ");
        }
    }

看到快排讲得不好,偷学左神的课了

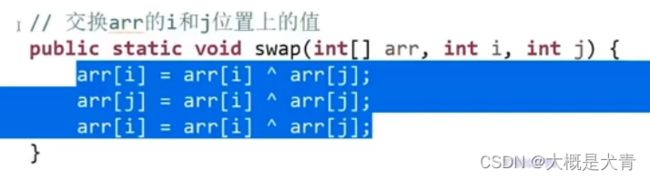
异或运算 — 相同为零,不同为1 ---- 也可以理解为无进位相加

交换函数,(要求ab是两块内存,什么意思,就是是两个内存地址的亦或,要求ab是两个地址不一样的内存地址?)

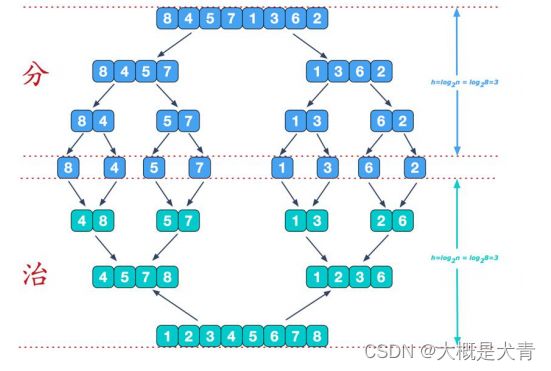
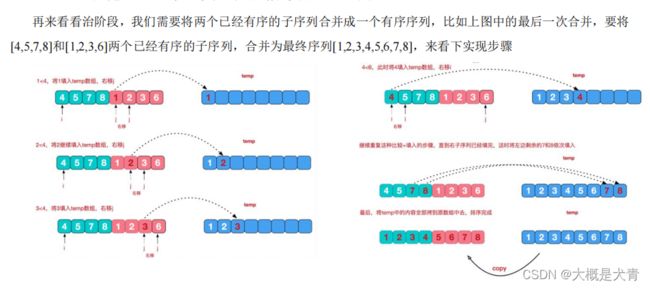
归并排序

思想介绍:经典的分治策略
思维图:


上代码:

    /**
     * 合并
     * @param arr   原始数组
     * @param left  左 初始索引
     * @param mid   中间索引,同时也是左数组的末尾索引 --- 右初始索引是mid+1
     * @param rigth 最右的元素的索引
     * @param temp
     */
    private void merge(int[] arr, int left, int mid, int rigth, int[] temp) {
        int i = left;//左有序数列的初始索引
        int j = mid + 1;//右有序数列的初始索引
        int t = 0; //temp数组的当前索引

        //(一)
        //先把左右两边的有序数,按照规则填充到temp数组,直到有一边的数组处理完毕
        while (i <= mid && j <= rigth) {
            //左较小,左填充到temp;否则右边
            if (arr[i] <= arr[j]) {
                temp[t] = arr[i];
                t++;
                i++;
            } else {
                temp[t] = arr[j];
                t++;
                j++;
            }
        }
//        (二)
        //把剩下的数据的一边的数据一次填充到temp
        while (i <= mid) {//左边 还有剩余
            temp[t] = arr[i];
            t++;
            i++;
        }

        while (j <= rigth) {//右边剩余...
            temp[t] = arr[j];
            t++;
            j++;
        }

//        (三)
        //temp数组的元素拷贝到arr
        //注意!不是每次都要拷贝...
        t = 0;
        int tempLeft = left;

        while (tempLeft <= rigth) {
            arr[tempLeft] = temp[t];
            t++;
            tempLeft++;
        }
    }

    /**
     * 分+合
     */
    public void mergeSort(int[] arr, int left, int rigth, int[] temp) {
        if (left < rigth) {
            int mid = (left + rigth) / 2;//中间索引
            //左递归分解
            mergeSort(arr, left, mid, temp);
            //右递归分解
            mergeSort(arr, mid + 1, rigth, temp);

            //合并
            merge(arr, left, mid, rigth, temp);
        }
    }

    @Test
    public void test_00(){
        int[] arr = {8, 4, 5, 7, 1, 3, 6, 2};
        int[] temp = new int[arr.length];//归并排序需要一个额外的空间

        mergeSort(arr, 0, arr.length - 1, temp);

        System.out.println(Arrays.toString(arr));
    }

好好感受里面的递归!

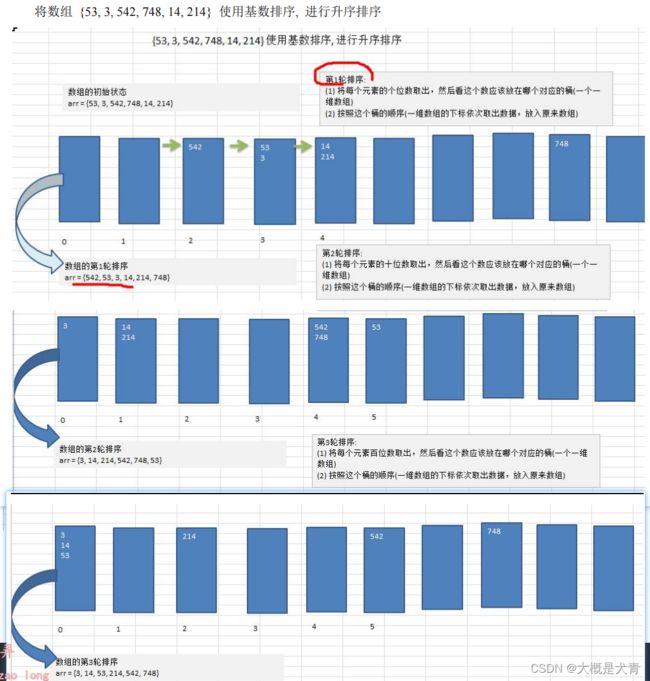
基数排序

介绍:
基数排序也叫做桶排序 ,稳定性排序(两个1,在前面的1还在前面),基数排序是桶排序的扩展.

图解和思想:
将数组,从最低位开始,一次比较,放到对应的桶子中去

上代码:

public void radixSort(int[] arr) {
    //1.确定数组最大数是几位数
    int max = arr[0];
    for (int i = 1; i < arr.length; i++) {
        if (arr[i] > max) {
            max = arr[i];
        }
    }
    //得到最大位数
    int maxLength = (max + "").length(); //把max变成字符串后求长度,就是最大位数
    int[][] bucket = new int[10][arr.length];//二位数组表示桶
    int[] bucketElementCounts = new int[10]; //各个桶存放的数据的个数 --- 这种方式创建数组,自动赋值全是 0
    // -- 例如bucketElementCount[0] --> 记录的是"0桶"的放入数据的个数

    //几轮排序 ---例子中是百位数,3轮
    for (int i = 0, n = 1; i < maxLength; i++, n *= 10) {//n是用来取个,十,百位的

        for (int j = 0; j < arr.length; j++) {//依次对待排序数组arr,按照位序排序
            //取出每个元素对应的值
            int digitOfElement = arr[j] / n % 10;
            //放入对应的桶子中
            bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
            bucketElementCounts[digitOfElement]++;
        }

        //按照这个桶的顺序,一次取出放回原数组arr中
        int index = 0;//arr的索引
        for (int k = 0; k < 10; k++) { //k就是k号桶           k < bucketElementCounts.length
            //如果桶中有数据,才放入
            if (bucketElementCounts[k] != 0) {
                //循环该桶,放入
                for (int l = 0; l < bucketElementCounts[k]; l++) {
                    arr[index++] = bucket[k][l];
                }
            }
            //处理完每个桶,需要把该桶的元素计数归零,bucketElementCounts[k] = 0
            bucketElementCounts[k] = 0;
        }
    }
}


@Test
public void test() {
    int[] arr = {53, 3, 542, 748, 14, 214};
    radixSort(arr);
    System.out.println(Arrays.toString(arr));
}
/**
 * 编程总结:
 * 1.首先是二维数组表示桶,桶的深度由arr的长度来决定
 * 2.其次比较关键的一个元素是bucketElementCounts[]数组
 * --->
 * i它的作用就很妙:首先长度是10,他的数据记录的是对应桶号里面的数据的个数,可以当作桶的深度来使用的
 * ii.注意每次把桶的数据取出来排序的时候,要把他的bucketElementCounts[k]的数据清零....
 *
 */

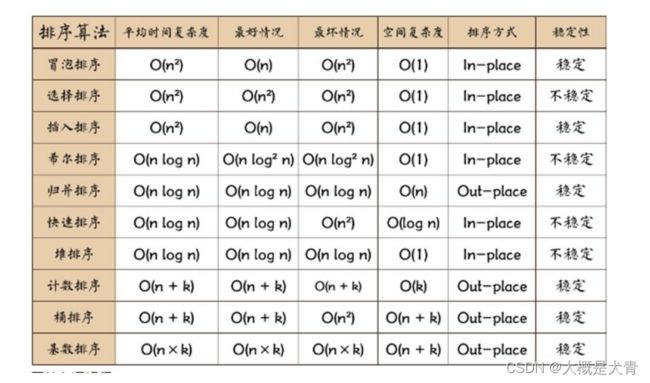
排序比较–

比较图