基于MATLAB的数字水印系统研究解析
一、课题背景景
二十一世纪是数字时代,通信技术的迅速发展和计算机网络的普遍运用,使人们可以通过互联网收发信息,可以随时上传自己创作的数字图象、音乐、视频等作品,可以进行学术交流。
然而,也正是由于网络的这种便捷性、传播迅速的优点使其很容易被非法拷贝,导致数字产品的版权、完整性、有效性得不到保证,严重损害了创作者的利益。而一些具有特殊意义的数字信息,如涉及司法诉讼、政府机要等信息,更是遭到了不法分子地恶意攻击和随意篡改等,这一系列问题给当今科学家带来了巨大挑战。
基于以上类似问题,数字水印技术可以说是信息时代的特有产物,是一种可以在开放网络环境下保护版权和认证来源及保障信息完整性的新型技术,在音频、图像、视频制品中迅速得到广泛的研究和发展。
二、 数字水印的基本特点
数字水印是加在数字图象、音频或视频中的微弱信号,这个信号是人们能够建立产品所有权、辨认购买者或提供数字产品的一些额外信息。具体说来,它们都具有以下共同的特征:
1. 不可感知性
对于数字水印的嵌入,应该对观察者没有视觉障碍,理想情况应该是水印图像与原始图像没有丝毫差别。
2. 鲁棒性
鲁棒性是指一个数字水印能够承受攻击的能力,一般来说数字水印方法是针对特定的攻击进行设计。
3. 安全性
水印技术的安全性是其最重要的特性,由于它的商业性,其算法必须公开,算法的安全性完全取决于密钥,而不对算法进行保密。
4. 计算复杂度
不同应用中,对于水印的嵌入算法和提取算法的计算复杂度要求是不同的,复杂度直接与水印系统的实时性相关。
5. 水印容量
水印容量是指载体数据字中可嵌入水印信息位的多少,可以从几兆到几个比特不等。
三、 数字水印的应用
数字水印是以不可感知的方式嵌入到数字信息中的,总体来说它有以下应用:
数字产品产权保护
这是数字水印最广泛的应用,将秘密的数字信号嵌入到有价值的数字文件中,这些数字信号是产权的标识,在不破坏数字文件的情况下不能被盗版者出去,起到了保护产权的作用。
1. 数据库标识
有时一些文件中提示数据的标识信息往往比文件本身更重要或者一些音像文件需要将说明注释(如字幕等)与音像本身结合起来,这就可以通过数字水印技术加以解决。
2. 文件内容鉴定
水印技术在鉴定数据建立者和鉴别数据内容有着特殊的运用,目的是检测数据是否被修改过或是否经过特殊的处理。
3. 系统升级
日常生活中常常涉及到旧装系统升级情况,这可以通过将“增强层”嵌入到所发送的数据中来给传统的信号发射系统升级。
4. 商务交易中的票据防伪
随着高质量图像输入输出设备的发展,使得货币、支票以及其他票据的伪造变得更加容易。目前,美国、日本以及荷兰都已开始研究用于票据防伪的数字水印技术。
5. 媒体侦破
这一运用的目的是提取对原始信号进行处理过的信息。例如,鉴定方法可以发现一幅图像被篡改过,但无法发现是怎样篡改的。媒体侦破技术就可以指出图像的哪部分被篡改了,指出被插入到原图像中的新对象等等。
四、傅立叶域水印理论基础
4.1 傅立叶变换简述
傅立叶变换(Fourier Transform)是研究信号的频谱方法,它架起了时域和频域之间的桥梁。打个比方来说,傅立叶变换就好比描述函数的第二种语言,能讲两种语言的人常常会发现,在表达某些观点时,一种语言会比另一种语言优越。类似地,图像处理者在解决某一问题时会在空域和频域之间来回切换。傅立叶变换把一个时域信号函数分解为众多的频率成分,这些频率成分又以准确地重构成原来的时域信号,这种变换是可逆的且保持能量不变。下面两个公式(3.1)、(3.2)给出了傅立叶变换及其逆变换:
从时域到频域称为Fourier 变换,从频域到时域称为逆Fourier 变换,信号函数f (t)和它的
Fourier变换F(ϖ )是同一能量信号的两种不同表现形式。
Fourier 分析理论十分完善,既可以处理连续的信号也可以处理离散的信号。计算机只能处
理离散的信号,于是离散Fourier 变换(DFT)成为计算机实现Fourier 变换的第一种形式。下面我
们仅讨论一维离散傅立叶变换和二维离散傅立叶变换。
3.1.1 一维离散傅立叶变换DFT
对一个连续函数f (t)等间隔采样得到一个离散序列。设共采样N 个数据。则这个离散序列
可表示为{f (0), f (1),L, f (N −1)},并令n为离散时域变量,k为离散频域变量,则可将傅立叶变
换对定义如下:
一般地, f (n)是实函数,F(k)是复函数,可以写成:
其中,R(k)、I (k)分别为复数的实部和虚部。下式为幅度函数,称为f (n)的傅立叶谱:
ϕ(k)称为相位函数:
既可以在幅度函数F(k) 上嵌入水印,也可以在相位函数ϕ (k)上嵌入水印。DFT中,如果f (n)为实函数,则一共需要N × N 次实数与复数的乘法,N × (N −1)次复数加法,一次实数与复数乘法需要两次实数乘法,一次复数加法需要两次实数加法,所以总共需要2N^2 次实数乘法,2N × (N −1)次实数加法,因此时间复杂度为O(N^2 ),当n很大时,计算机是无法接受的。因此人们想出了快速傅立叶变换。
五、 水印算法
1、 算法原理
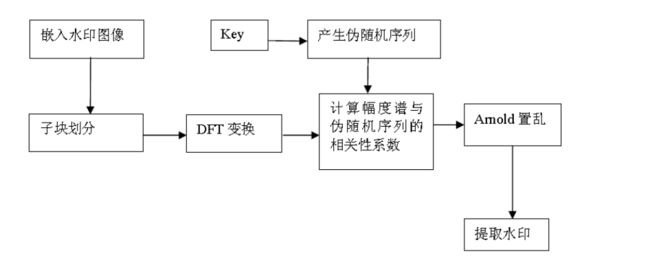
图 5.1 水印嵌入流程图图5.1 是嵌入算法流程图。为了提高传统相关性检测方法的准确率,本算法采取嵌入两个不相关伪随机序列的方法,有效的提高了提取的准确率。首先将原始图像划分子块,对每一图像块进行DFT变换,将二值水印图像用Arnold变换置乱。产生两个伪随机序列。置乱水印矩阵值为0时用一个伪随机序列与原始图像的幅度谱进行乘性叠加,矩阵值为1时,用另一个伪随机序列与原始图像幅度谱进行乘性叠加。
5.2 提取算法原理
水印提取算法是嵌入算法的逆过程
- 实现过程
程序见附录
原始宿主图像是384*384*8b 的lena 灰度测试图像,见图6.1
而水印图像是一幅40*40*1b 的二值图像,见图4.4,水印检测不需要原始图像.但需要原始水印图像的尺寸信息。
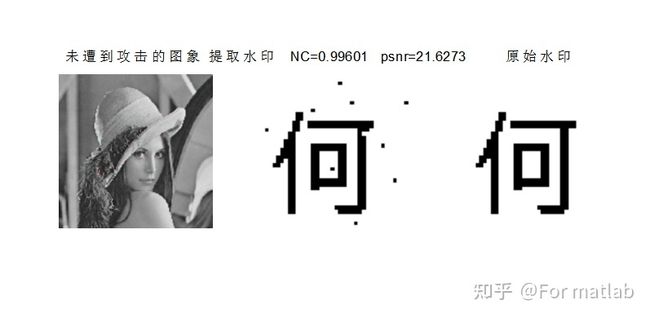
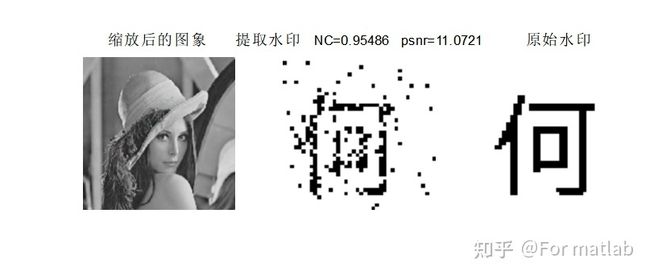
下图是用Matlab 软件进行试验的结果:
6.3 水印置乱 图6.4 嵌入水印图像与原始图像从以上结果可以看出,从没有遭受攻击的图像中提取出来的水印与原始水印的相关性最好,为0.99601,接近于1,满足设计要求。当对图像分别进行剪切攻击、噪声攻击、缩放攻击与压缩攻击后,提取出来的水印与原始水印的相关性依次降低,同时峰值信噪比也依次降低。特别是进行了压缩攻击后提取水印与原始水印相关性NC为0.83534,基本上分辨不出来了,峰值信噪比也大幅度降低。因此,可以看出,基于DFT域的数字水印算法抗剪切攻击能力比较强,其次为抗噪声攻击能力与抗缩放攻击能力,而抗压缩攻击能力较差。
- 部分参考源码
水印嵌入源码
%基于傅立叶域的数字水印
%注意:水印必须为40*40的二值图像
%因为40阶的二维arnold置乱周期为30,所以嵌入时置乱8次,提取时置乱22.可以根据自己的需要更改.
%嵌入源码
clc
clear all;
% 保存开始时间
start_time=cputime;
iTimes=8; %置乱次数
k=1.1; % 设置嵌入强度系数
blocksize=8; % 块的大小
filter_m=[ 1,1,1,1,1,1,1,1; % 滤波矩阵
1,1,1,1,1,1,1,1;
1,1,0,0,0,0,1,1;
1,1,0,0,0,0,1,1;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;];
% 读入原始图像
file_name='lena.bmp';
cover_object=double(imread(file_name))/255;
% 原始图像矩阵的行数与列数
Mc=size(cover_object,1);
Nc=size(cover_object,2);
% 最大嵌入信息量
max_message=Mc*Nc/(blocksize^2);
% 读入水印图像
file_name='watermark.bmp';
message=double(imread(file_name));
%水印图像矩阵的行数与列数
Mm=size(message,1);
error('必须为40*40大小,或者修改置乱次数');
end
tempImg=message;
message_vector=reshape(outImg,1,Mm*Nm)
% 将cover_object(原图矩阵)写入watermarked_image
watermarked_image=cover_object;
%置随机数发生器的状态为1100
key=1100;
rand('state',key);
% 产生伪随机序列
pn_sequence_zero=round(2*(rand(1,sum(sum(filter_m)))-0.5));
pn_sequence_one=round(2*(rand(1,sum(sum(filter_m)))-0.5));
% 将图像分块
x=1;
y=1;
h=waitbar(0,'嵌入水印,请等待');
for (kk = 1:length(message_vector))
% 做傅立叶变换
fft_block=fft2(cover_object(y:y+blocksize-1,x:x+blocksize-1));
%计算幅值
abs_block=fftshift(abs(fft_block));
%计算相位
angle_block=angle(fft_block);
% 当message_vector=0且filter_m=1时用伪随机序列pn_sequence_zero叠加abs_block
% 当message_vector=1且filter_m=1时用伪随机序列pn_sequence_one叠加abs_block
ll=1;
if (message_vector(kk)==0)
abs_block(blocksize-ii+1,blocksize-jj+1)=abs_block(blocksize-ii+1,blocksize-jj+1)+…
abs_block(ii,jj)-abs_block_o;
ll=ll+1;
end
end
end
else
for ii=1:blocksize
for jj=1:blocksize
if (filter_m(ii,jj)==1)
abs_block_o=abs_block(ii,jj);
abs_block(ii,jj)=abs_block(ii,jj)*(1+k*pn_sequence_one(ll));
abs_block(blocksize-ii+1,blocksize-jj+1)=abs_block(blocksize-ii+1,blocksize-jj+1)+…
abs_block(ii,jj)-abs_block_o;
ll=ll+1;
end
end
end
end
% 进行傅立叶逆变换
abs_block=fftshift(abs_block);
watermarked_image(y:y+blocksize-1,x:x+blocksize-1)=…
abs(ifft2(abs_block.*exp(i*angle_block)));
% 移动到下一块
waitbar(kk/length(message_vector),h);
end
close(h);
% 转换为uint8,并写入
watermarked_image_int=uint8(watermarked_image*255);
imwrite(watermarked_image_int,'dft2_watermarked.bmp','bmp');
% 计算运行时间
elapsed_time=cputime-start_time,
% 计算psnr
psnr=psnr(cover_object,watermarked_image),
% 显示水印,嵌入水印图像与原始图像
figure(1)
subplot(1,2,1)
imshow(message,[]);
title('原始水印');
subplot(1,2,2);
imshow(tempImg,[]);
title('置乱水印');
figure(2)
subplot(1,2,1)
imshow(watermarked_image,[]);
name='嵌入水印图像';
title(strcat(num2str(name),' k=',num2str(k),' psnr=',num2str(psnr)));
subplot(1,2,2)
imshow(cover_object,[])
title('原始图像');
%%%%%%%%%%%%%% 进行攻击测试 %%%%%%%%%%%
disp(‘1-->加入白噪声’);
disp(‘2-->剪切图像’);
disp(‘3-->直接检测’)
begin=input(‘请选择攻击(1-3):’)
switch begin
%%%%%%% 加入白噪声 %%%%%%%%
case 1
figure(3)
Aimage1=wimage;
Wnoise=0.01*randn(size(Aimage1));
Aimage1=Aimage1+Wnoise;
subplot(1,3,1),imshow(Aimage1,[]),title(‘加入白噪声后的图象’);
att=Aimage1;
imwrite(att,'chulihouimage.bmp');
%%%%%%%% 剪切攻击 %%%%%%%%
case 2
figure(3)
水印提取源码
%提取源码
clc
clear all;
% 保存开始时间
start_time=cputime;
iTimes=22; %置乱次数
blocksize=8; % 设置块的大小
filter_m=[ 1,1,1,1,1,1,1,1; % 滤波矩阵
1,1,1,1,1,1,1,1;
1,1,0,0,0,0,1,1;
1,1,0,0,0,0,1,1;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;];
% 读入嵌入水印图像
file_name='chulihouimage.bmp';
watermarked_image=double(imread(file_name))/255;
% 嵌入水印图像矩阵的行数与列数
Mw=size(watermarked_image,1);
Nw=size(watermarked_image,2);
% 最大可嵌入信息量
max_message=Mw*Nw/(blocksize^2);
% 读入原始水印
file_name='watermark.bmp';
orig_watermark=double(imread(file_name));
% 原始水印矩阵的行数与列数
Mo=size(orig_watermark,1);
No=size(orig_watermark,2);
%置随机数发生器的状态为1100
key=1100;
rand('state',key);
% 产生伪随机序列
pn_sequence_zero=round(2*(rand(1,sum(sum(filter_m)))-0.5));
pn_sequence_one=round(2*(rand(1,sum(sum(filter_m)))-0.5));
% 将图像分块
x=1;
y=1;
h=waitbar(0,'提取水印,请等待');
for (kk = 1:max_message)
% 傅立叶变换
fft_block_w=fft2(watermarked_image(y:y+blocksize-1,x:x+blocksize-1));
abs_block_w=abs(fftshift(fft_block_w));
ll=1;
for ii=1:blocksize
for jj=1:blocksize
if (filter_m(ii,jj)==1)
sequence(ll)=abs_block_w(ii,jj);
ll=ll+1;
end
end
end
% 计算sequence与pn_sequence_zero和pn_sequence_one的相关系数
correlation_zero(kk)=corr2(pn_sequence_zero,sequence);
correlation_one(kk)=corr2(pn_sequence_one,sequence);
% 移动到下一块
if (x+blocksize) >= Nw
x=1;
y=y+blocksize;
else
x=x+blocksize;
end
waitbar(kk/max_message,h);
end
close(h);
% 如果correlation_zero>correlation_one,那么message_vector=0,反之为1.
for (kk=1:Mo*No)
if correlation_zero(kk)>correlation_one(kk)
message_vector(kk)=0;
else
message_vector(kk)=1;
end
end
% Arnold置乱
tempImg=reshape(message_vector(1:Mo*No),Mo,No);
message_arnold=tempImg;
for n=1:iTimes % 次数
for u=1:Mo
for v=1:No
temp=tempImg(u,v);
ax=mod(u+v,Mo)+1;
ay=mod(u+2*v,No)+1;
outImg(ax,ay)=temp;
end
end
tempImg=outImg;
end
message=outImg;
% 计算运行时间
elapsed_time=cputime-start_time,
%计算NC(归一化相关系数)
NC=nc(message,orig_watermark)
%计算 psnr
psnr=psnr(message,orig_watermark);
% 显示提取水印与原始水印
figure(3)
subplot(1,3,2);
imshow(message,[]);
name='提取水印';
title(strcat(num2str(name),' NC=',num2str(NC), ' psnr=',num2str(psnr)
));
subplot(1,3,3)
imshow(orig_watermark,[])
title('原始水印');