【算法导论】摊还分析

一、摊还分析简介

  在摊还分析中，我们求数据结构的一个序列操作中所执行的所有操作的平均时间，来评价操作的代价。这样，我们就可以说明一个操作的平均代价是很低的，即使序列中某个单一操作的代价很高。摊还分析不同于平均情况，它并不涉及概率，它可以保证最坏情况下每个操作的平均性能。

二、分析的两个问题

  本文我们将用三种方法求解以下两个问题的摊还代价。

1.栈操作

最原始的栈有两种基本操作分别是：

• PUSH(S，x)：将对象 x 压入栈 S 中。
• POP(S)：将 S 的栈顶对象弹出，并返回该对象。

  由于两个操作的时间都是 $O(1)$ 的，我们假定其代价为均为1，因此 n 个PUSH和POP操作的序列的总代价为 n，而 n 个操作的实际运行时间为 $\theta (n)$。
  现在我们增加一个新的栈操作 MULTIPOP(S，k)，它删除栈 S 栈顶的 k 个对象，如果栈中对象数小于k，则将整个栈中的的内容都弹出以下是其执行伪代码：

MULTIPOP(S,k)
	while not STACK-EMPTY(S) and k > 0 //STACK-EMPTY(S)判断S栈是否为空，空则返回false
		POP(S)
		k = k - 1

  在一个包含s个对象的栈上执行 MULTIPOP(S,k) 操作有两种结果，当 s > k时，则执行 k 次 POP 操作，当 s < k 时，则执行 s 次操作。由以上分析可知 MULTIPOP 的总代价为 $min(s,k)$。
  在下文中，我们将用三种方式来分析一个由 n 个PUSH、POP和 MULTIPOP 组成的操作序列在一个空栈上的摊还代价。

2. 二进制计数器递增

  该问题为 k 位二进制计数器的递增问题，计数器的初值为0。我们用一个位数组$A[\mathrm{0...}k-1]$最为计数器，其中 $A.length=k$。当计数器中保存的二级制为 x 时，x的最低位保存在 $A[0]$ 中，而最高位保存在 $A[k-1]$ 中，因此 $x={\sum }_{i=0}^{k-1}A[i]\ast 2^i$。计数器的一次递增过程用一下代码来实现：

INCREMENT(A)
	i = 0
	while i < A.length and A[i] == 1
		A[i] = 0
		i = i + 1
	if i < A.length
		A[i] = 1

计数器计数过程：

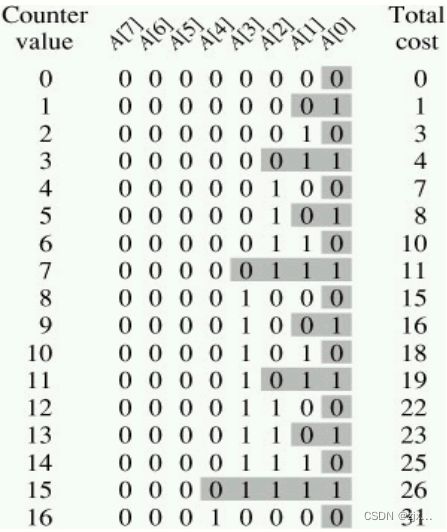
  通过代码和图示我们可知，位数组 A 的变化过程为从下标为0开始向高位遍历，将值为1的位反转为0，将第一次出现的值为0的位反转为1。
  在下文中，我们将用三种方式来分析该二进制递增计数器的摊还代价。

三、分析方法

1. 聚合分析

  利用聚合分析，我们证明对所有 n，一个操作的序列最坏情况下花费的总时间为 $T(n)$。因此，在最坏情况下，每个操作的平均代价，或摊还代价为 $T(n)/n$。

1.1 栈操作

  我们来分析一下一个由 n 个PUSH、POP和 MULTIPOP 组成的操作序列在一个空栈上的执行情况。因为栈的大小最大为 n，所以序列中一个MULTIPOP操作的最坏情况（执行n次POP）代价为 $O(n)$，所以 n 个操作的序列的最坏情况代价为 $O(n^2)$（在操作序列为$O(n)$个MULTIPOP操作的情况下），这种分析是正确的，但显然在实际情况下不可能实现（因为不可能一直都是退栈操作），所以我们将使用聚合分析来得到一个更好的分析结果。
  当将一个对象压入栈后，我们至多将其弹出一次。因此对于一个非空的栈，可以执行的POP操作的次数（包括了MULTIPOP中调用的POP的次数）最多与PUSH的次数相当，即最多$O(n)$次。因此对任意的n值，任意一个由 n 个PUSH、POP和MULTIPOP组成的操作序列，最多花费$O(n)$的时间。一个操作的平均时间为$O(n)/n=O(1)$。在聚合分析中，我们将每个操作的摊还代价设定为平均代价。因此，在此例中，所有三种栈操作的摊还代价都是$O(1)$。

1.2 二进制计数递增

  当数组A所有位都是1时，INCREMENT执行一次花费的时间为$\theta (k)$，因此对于初值为0的计数器执行n个INCREMENT操作最坏情况下花费 $O(nk)$。
  我们用聚合分析得到一个更紧的界—最坏情况下代价为 $O(n)$，因为不可能每次INCREMENT操作都反转所有的二进制位，如问题中的图所示，每次调用INCREMENT时$A[0]$都会反转，而下一位的$A[1]$是每两次调用翻转一次，这样，对一个初值为0的计数器执行一个n个INCREMENT操作的序列，只会使$A[1]$反转$\lfloor n/2\rfloor$次，类似的$A[2]$每四次调用才反转一次，执行一个n个INCREMENT操作的序列的过程中只会反转$\lfloor n/4\rfloor$次，所以一般情况下，对一个初值为0的计数器，执行n个INCREMENT操作的序列的过程中，$A[i]$会反转$\lfloor n/2^i\rfloor$次，对 $i\ge k$，$A[i]$不存在，因此也就不会反转。综上所述，在执行INCREMENT序列的过程中进行的反转操作的总数为：
$$\sum _{i=0}^{k-1}\lfloor \frac{n}{2^i}\rfloor <n\sum _{i=0}^{\infty }\lfloor \frac{1}{2^i}\rfloor =2n$$
  因此，对一个初值为0的计数器，执行一个n个INCREMENT操作的序列的最坏情况时间为$O(n)$。每个操作的平均代价，即摊还代价为$O(n)/n=O(1)$。

2.核算法

  在用核算法进行摊还分析时，我们对不同操作赋予不同费用，赋予某些操作的费用可能多于或少于其实际代价。我们将赋予一个操作的费用称为它的 摊还代价。当一个操作的摊还代价超过其实际代价时，我们将差额存入数据结构中的特定对象，存入的差额称为 信用。对于后续操作中摊还代价小于实际代价的情况，信用可以用来支付差额。因此，我们可以将一个操作的摊还代价分解为其实际代价和信用（存入的或用掉的）。

2.1 栈操作

其中栈操作中的三个操作的的实际代价为：

• PUSH     1
• POP     1
• MULTIPOP   $min(k,s)$  k 为MULTIPOP中的参数，s为调用时栈的规模。

我们为这些操作赋予如下摊还代价：

• PUSH     2
• POP     0
• MULTIPOP   0

  假定使用1美元来表示一个单位操作的代价，我们将一美元用来支付压栈操作的实际代价，将剩余的一美元存为信用（共缴费2美元），在任何时间点，栈中的元素都存储了与之对应的一美元的信用，该信用用来作为将来它被弹出栈时代价的预付费，当执行一个POP操作时，并不会缴纳任何费用，而是使用存储在栈中的信用来支付其实际代价，对于MULTIPOP操作，我们也可以不缴纳任何费用。
  由于栈中的元素是非负的，所以信用值也是非负的，因此，对于任意 $n$ 个PUSH、POP、MULTIPOP操作组成的序列，总摊还代价为实际总代价的上界。由于总摊还代价为 $O(n)$ ，因此总实际代价也为 $O(n)$。

2.2 二进制计数器递增

  对于该例，我们仍使用1美元表示一个单位的代价，对于一次置位操作，我们设其摊还代价为2美元，当置位时，用1美元支付置位操作的实际代价，并将另1美元置为信用，用来支付复位操作时的代价。
  由代码可知，INCREMENT过程之多置位一次，因此其摊还代价最多为2美元，计数器中1的个数永远不会为负因此，任何时刻信用值都是非负的。所以，对于 $n$ 个INCREMENT操作，总的摊还代价为 $O(n)$，为总实际代价的上界。

3. 势能法

  我们将对一个初始数据结构 $D_0$ 执行 $n$ 个操作。对每个 $i=1,2,\mathrm{3...},n$，令 $c_i$ 为第 $i$ 个操作的实际代价，令$D_i$为在数据结构 $D_{i-1}$ 上执行第 $i$ 个操作得到的结果数据结构。势函数 $\varphi$ 将每个数据结构 $D_i$映射到一个实数 $\varphi (D_i)$ ，此即为关联到数据结构 $D_i$ 的势。第 $i$ 个操作的摊还代价 $\widehat{c_i}$ 用势函数定义为：
$$\widehat{c_i}=c_i+\varphi (D_i)-\varphi (D_{i-1})$$因此，每个操作的摊还代价等于其实际代价加上此操作引起的势能变化，由此可得，n个操作的总摊还代价为$$\begin{array}{rl}\sum _{i=1}^n\widehat{c_i}& =\sum _{i=1}^n(c_i+\varphi (D_i)-\varphi (D_{i-1}))\\ & =\sum _{i=1}^n{c}_i+\varphi (D_n)-\varphi (D_0)\end{array}$$

3.1 栈操作

  我们将栈的势函数定义为其中的对象的数量。对于初始的空栈 $D_0$，我们有 $\varphi (D_0)=0$，由于栈中的对象数目不可能为负，因此，第 $i$ 步操作具有非负的势，即
$$\varphi (D_i)\ge 0=\varphi (D_0)$$因此用 $\varphi$ 定义的 n 个操作的总摊还代价即为实际代价的一个上界。

下面计算不同栈操作的摊还代价：

• 如果第 i 个操作是 PUSH 操作，此时栈中包含 s 个对象，则势差为：
  $$\varphi (D_i)-\varphi (D_{i-1})=(s+1)-s=1$$所以其摊还代价为：$$\widehat{c_i}=c_i+\varphi (D_i)-\varphi (D_{i-1})=1+1=2$$
• 如果第 i 个操作是 MULTIPOP(S,k)，将 $k^{{}^{\prime }}=min(k,s)$ 个对象弹出栈。对象的实际代价为$k^{{}^{\prime }}$，势差为$$\varphi (D_i)-\varphi (D_{i-1})=-k^{{}^{\prime }}$$因此，其摊还代价为$$\widehat{c_i}=c_i+\varphi (D_i)-\varphi (D_{i-1})=k^{{}^{\prime }}-k^{{}^{\prime }}=0$$类似的，普通POP操作的摊还代价也为0。

  每个操作的摊还代价都是 $O(1)$，因此，n 个操作的总摊还代价为 $O(n)$。由于我们已经论证了$\varphi (D_i)\ge \varphi (D_0)$，因此，n个操作的总摊还代价为实际总摊还代价的上界。所以 n 个操作的最坏情况时间为 $O(n)$。

3.2 二进制计数器递增

   这一次，我们将计数器执行 $i$ 次INCREMENT操作后的势定义为 $b_i$— $i$ 次操作后计数器中 1 的个数。
   假设第 $i$ 个INCREMENT操作将 $t_i$ 个位复位，则其实际代价至多为 $t_i+1$，因为除了复位 $t_i$ 个位之外，还至多置位 1 位。如果 $b_i=0$，则第 i 个操作将所有 $k$ 位复位了，因此 $b_i=t_i=k$。如果 $b_i>0$，则 $b_i=b_{i-1}-t_i+1$。无论哪种情况，$b_i\le b_{i-1}-t_i+1$，势差为：
$$\varphi (D_i)-\varphi (D_{i-1})\le (b_{i-1}-t_i+1)-b_{i-1}=1-t_i$$因此，其摊还代价为$$\widehat{c_i}=c_i+\varphi (D_i)-\varphi (D_{i-1})\le (t_i-1)+(1-t_i)=2$$如果计数器从 0 开始，则 $\varphi (D_0)=0$。由于对所有的 $\varphi (D_i)\ge 0$，因此，一个从 $n$ 个INCREMENT操作的序列的总摊还代价是总实际代价的上界，所以 n 个INCREMENT操作的最坏情况时间为 $O(n)$。

  即使计数器不是从0开始也可以分析。假设计数器初始时包含 $b_0$ 个 1，经过 n 个INCREMENT操作后包含 $b_n$个 1，其中 $0\le b_0，b_n\le k$ 于是可以将公式改写为$$\sum _{i=1}^n{c}_i=\sum _{i=1}^n\widehat{c_i}-\varphi (D_n)+\varphi (D_0)$$对所有 $1\le i\le n$，我们有 $\widehat{c_i}\le 2$。由于 $\varphi (D_0)=b_0$且 $\varphi (D_n)=b_n$，n 个INCREMENT操作的总实际代价为$$\sum _{i=1}^n{c}_i\le \sum _{i=1}^{n}2-b_n+b_0=2n-b_n+b_0$$由于 $b_0\le k$ ，因此只要 $k=O(n)$，总实际代价就是 $O(n)$。换句话说，如果至少执行 $n=\Omega (k)$ 个INCREMENT操作，不管计数器初值是什么，总代价都是 $O(n)$。