面试算法题：二叉树的平衡性检测

更详细的讲解和代码调试演示过程，请参看视频
如何进入google,算法面试技能全面提升指南

如果你对机器学习感兴趣，请参看一下链接：
机器学习：神经网络导论

二叉树由于其结构化清晰，并且变种多样，是面试中极为常见的考题。从本节开始，我们进入到有关二叉树面试题的研究中。

二叉树自身存在着一种递归结构，一个节点除了含有值外，还含有两个节点指针，这两个指针又分别指向两颗二叉树。二叉树有一个很重要的概念叫做树的高，它指的的是从某个节点开始，抵达某个叶子节点的最长路径。例如给定下面的二叉树：

如果从根节点6算起，二叉树的高度为4，因为它有4个层级，那么6的左子树，它的高度就为3，以此类推。

如果一颗二叉树是平衡的，必须满足每个节点，它左子树和右子树高度只差不超过1. 问题是，给定一颗二叉树的根节点，给出算法，判断该二叉树是否是一颗平衡二叉树。

如果一棵二叉树是空的，那么我们认为它的高度为0.
对于任意叶子节点，有就是节点的左右子树为空，那么它的高度为1.
对于非叶子节点，它的高度是先计算它的左右子树的高度，那么它本身的高度就是左右子树的最大高度加1.

由此，这道题的解决思路是计算每个节点左右子树的高度，如果两者高度只差大于1，那么它不是平衡的，如果每个节点左右子树的高度只差不超过1，那么他就是一棵平衡二叉树。

二叉树的高度可以递归来计算：
1. 如果输入的是空节点，那么返回高度值0
2. 如果输入的是叶子节点，那么返回高度1
3. 如果输入的是非叶子节点，那么分别计算左右子树的高度，选取其中最大者加1作为本节点的高度。

根据上面思路，我们实现的算法如下：

public class BalancedTree {
    private boolean balanced = true;

    public boolean isTreeBalanced(TreeNode node) {
        computeTreeHeight(node);
        return balanced;
    }


    private int computeTreeHeight(TreeNode node) {
        if (node == null) {
            return 0;
        }

        int leftHeight = computeTreeHeight(node.left);
        int rightHeight = computeTreeHeight(node.right);
        int height = leftHeight > rightHeight ? leftHeight : rightHeight;

        if (Math.abs(rightHeight - leftHeight) > 1) {
            balanced = false;
        }
        return height + 1;
    }
}

computeTreeHeight 接收的参数是一个二叉树的节点，然后分别计算该节点的左右子树高度，然后根据结果计算自身高度，在计算过程中，如果发现左右子树高度超过1，那么把balanced 设置成false, 如果该值设置成false的话，那么该二叉树就不是平衡的。

我们看看二叉树节点的定义和构造：

public class TreeNode {
    public int vaule;
    public TreeNode left;
    public TreeNode right;

    public TreeNode(int v) {
        this.vaule = v;
        this.left = this.right = null;
    }
}


public class TreeUtil {
    private TreeNode root = null;
    public void addTreeNode(TreeNode node) {
        if (root == null) {
            root = node;
            return;
        }

        TreeNode cur = root, prev = root;
        while (cur != null) {
            prev = cur;
            if (cur.vaule > node.vaule) {
                cur = cur.left;
            } else {
                cur = cur.right;
            }
        }

        if (prev.vaule > node.vaule) {
            prev.left = node;
        } else {
            prev.right = node;
        }
    }

    public TreeNode getTreeRoot() {
        return root;
    }
}

TreeUtil用来构建一棵二叉树，它构建的是一棵排序二叉树，如果加入的节点比当前节点值小，那么把节点加入当前节点的左子树，如果加入节点的值比当前节点值大，那么把节点加入当前节点的右子树。我们再看看主函数入口处代码：

public class BinaryTree {
   public static void main(String[] s) {
       int[] arr = new int[]{6,4,9,2,5,7,10,1,3,8};
        TreeUtil util = new TreeUtil();
        for (int i = 0; i < arr.length; i++) {
            TreeNode n = new TreeNode(arr[i]);
            util.addTreeNode(n);
        }

        TreeNode root = util.getTreeRoot();
        BalancedTree bt = new BalancedTree();
        boolean isBalanced = bt.isTreeBalanced(root);

        System.out.println("If the binary tree is banlanced ? the answer is : " + isBalanced);
public class BinaryTree {
   public static void main(String[] s) {
       int[] arr = new int[]{6,4,9,2,5,7,10,1,3,8};
        TreeUtil util = new TreeUtil();
        for (int i = 0; i < arr.length; i++) {
            TreeNode n = new TreeNode(arr[i]);
            util.addTreeNode(n);
        }

        TreeNode root = util.getTreeRoot();
        BalancedTree bt = new BalancedTree();
        boolean isBalanced = bt.isTreeBalanced(root);

        System.out.println("If the binary tree is banlanced ? the answer is : " + isBalanced);

        util.addTreeNode(new TreeNode(11));
        util.addTreeNode(new TreeNode(12));
        util.addTreeNode(new TreeNode(13));
        root = util.getTreeRoot();
        isBalanced = bt.isTreeBalanced(root);
        System.out.println("If the binary tree is banlanced ? the answer is : " + isBalanced);

   }
}

   }
}

开始的for 循环利用TreeUtil构建了前面图像所示的二叉树，然后获得该二叉树的根节点，然后使用BalancedTree来检验该二叉树是否平衡，通过观察我们知道，该二叉树每个节点的左右子树高度不超过1，所以该二叉树是平衡的。

接下来，我们又给二叉树加入三个节点，节点值分别为11，12，13，于是二叉树如图所示：

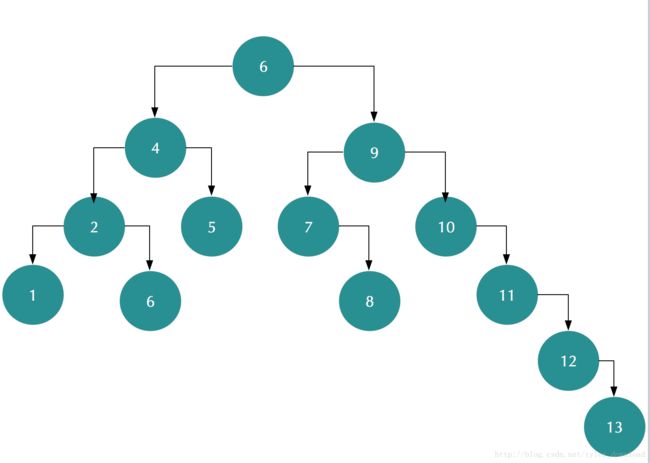
此时我们可以看到，节点10的左子树是空，因此左子树的高度是0，右子树的高度是3，左右子树的高度相差超过了1，所以此时该二叉树是不平衡的。如果运行代码，可以发现，我们的代码能给出去正确的判断，因此代码对算法的实现是正确的。

该算法主要是递归的去计算每个节点的高度，在计算过程中，每个节点最多被访问1次，因此算法的复杂度是O(n)，算法没有申请新内存因此算法的空间复杂度是O(1).

更详细的解释和代码演示，请参看视频。
更多技术信息，包括操作系统，编译器，面试算法，机器学习，人工智能，请关照我的公众号：